贝叶斯分析法在市场调研中的应用
一、市场调研的需求场景
在营销活动的用研调研时,我们经常会去问用户在不同平台的品类付费情况,以对比大促期间本品和竞品分别在哪些品类上具有市场优势,他们之间的差距具体在哪里、差距有多大。假如根据调研问卷结果,我们知道拼多多用户有30%的人在大促购买生鲜类,而淘宝用户只有26%的人购买了生鲜,那么我们能够得出结论说大促期间更多人来拼多多购买生鲜,拼多多生鲜具有明显的品类优势吗?
其实不然,这种忽略了前提条件的情况很可能会让我们根据主观经验做出错误的判断,即我们忽略了平台市场规模的影响。“在拼多多购买了生鲜”和“买生鲜的人是在拼多多买的”是两个完全不同的事情,假如拼多多只是一个小型生鲜网购平台,在该平台购买生鲜的用户比例肯定会很高;但放之全市场,由于用淘宝的人更多,虽然只有26%的淘宝用户购买了生鲜,但市场上生鲜品类售卖表现好的平台依然是淘宝。
当我们进行平台优势对比时,一定要注意根据前提条件进行比例修改。让我们看看贝叶斯法则是如何对该类分析提供指导的:
二、贝叶斯分析法是什么
贝叶斯法则由英国数学家贝叶斯(Thomas Bayes)于1763年提出,用来描述两个条件概率之间的关系(即P(A|B)和P(B|A))。通常情况下,事件A在事件B发生的情况下出现,和事件B在事件A发生的情况下出现的概率是不同的(如下图所示),这是因为事件A和B发生的概率本身就不一样。
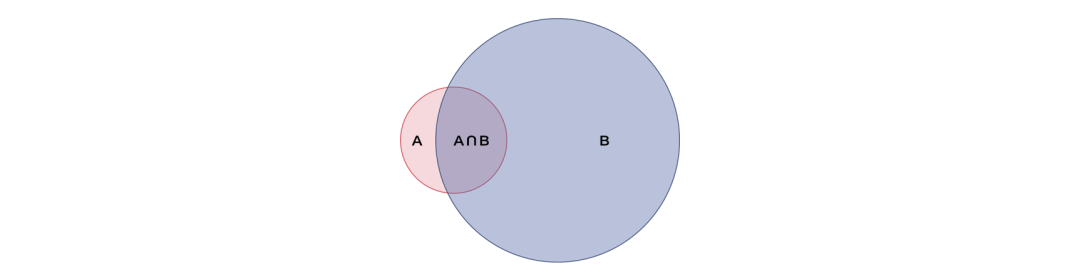
在具体介绍贝叶斯公式之前,我们需要先简单明
相关文章:

贝叶斯分析法在市场调研中的应用
一、市场调研的需求场景 在营销活动的用研调研时,我们经常会去问用户在不同平台的品类付费情况,以对比大促期间本品和竞品分别在哪些品类上具有市场优势,他们之间的差距具体在哪里、差距有多大。假如根据调研问卷结果,我们知道拼多多用户有30%的人在大促购买生鲜类,而淘宝…...
JavaEE——MyBatis将查询结果集封装进POJO实体类
简单介绍 在之前的我们比较详细的介绍过MyBatis的配置信息的时候,在SQL映射文件中说过我们可以直接将结果集映射到我们的POJO实体类中,省去了我们自己处理查询结果集的时间和代码,接下来我们就来演示将单条数据和多条数据映射到我们POJO实体…...

C++11 包装器function
文章首发公众号:iDoitnow C提供了多个包装器,它们主要是为了给其他编程接口提供更一致或更合适的接口。C11提供了多个包装器,这里我们重点了解一下包装器function。 对于function, C 参考手册给出的定义为: 类模板 std::function…...

XCP实战系列介绍14-基于Vector_Davinci工具的XCP配置介绍(三)
本文框架 1.概述2. 其他模块配置2.1 XCP初始化3. 手工代码部分3.1 周期函数添加3.2 DAQ Event调用3.3 XCP模块本身代码3.4 标定量的添加1.概述 在对XCP的配置部分介绍中我们计划分别对通讯部分配置、XCP模块本身配置及其他相关模块配置三篇进行介绍,在前两篇我们介绍了XCP配置…...

计算机图形学:中点BH算法对任意斜率的直线扫描转换方法
作者:非妃是公主 专栏:《计算机图形学》 博客地址:https://blog.csdn.net/myf_666 个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩 文章目录专栏推荐专栏系列文章序一、问题提出二、…...
(十一)、用户中心页面【uniapp+uinicloud多用户社区博客实战项目(完整开发文档-从零到完整项目)】
1,个人中心页面 1.1 新建个人中心页面 1.2 纯净版个人中心页面代码: <template><view class"user"><view class"top"><view class"group"><view class"userinfo"><!-- 顶部 左侧 头像 …...

LA@复数和复矩阵@实对称阵相关定理
文章目录复数🎈复矩阵和复向量共轭矩阵性质定理实对称阵的相关定理复数🎈 复数 (数学) (wikipedia.org) 加法:(abi)(cdi)(ac)(bd)i)减法:(abi)−(cdi)(a−c)(b−d)i)乘法:(abi)(cdi)acbciadibdi2(ac−bd)(bcad)i除法&…...

cmd set命令笔记
使用 set是cmd最基础的命令,每个人都会用,但其实它还是有些知识的。 set 用来接收入参 set /p var请选择(1或2或3): echo %var%可以接收输入的参数。 set /p var请选择(1或2或3): echo %var% 语法 he…...
IB学校获得IBO授权究竟有多难?
IB 学校认证之路,道阻且长 The road to IB school accreditation is long and difficult一所学校能获得IB授权必须经过IBO非常严格的审核,在办学使命&教育理念、组织架构、师资力量&授课技能、学校硬件设施和课程体系上完全符合标准才可获得授权…...
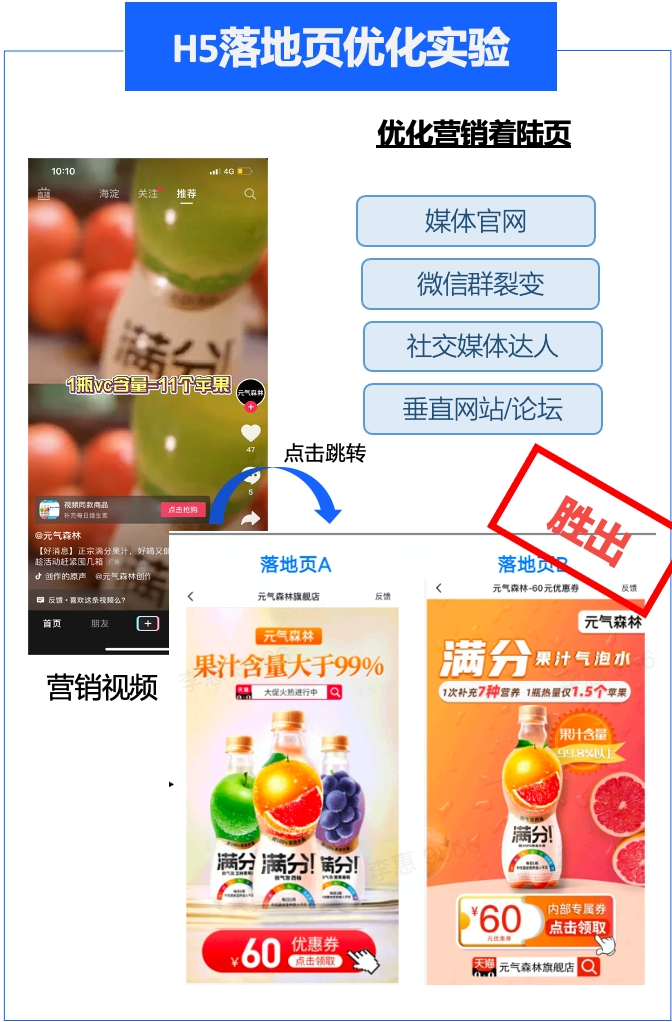
火山引擎 DataTester:A/B 测试,让企业摆脱广告投放“乱烧钱”
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,回复【1】进入官方交流群 在广告投放的场景下,一线广告优化师通常会创建多个计划,去测试不同的广告素材效果。这套方法看似科学,实际上却存在诸多问题&…...
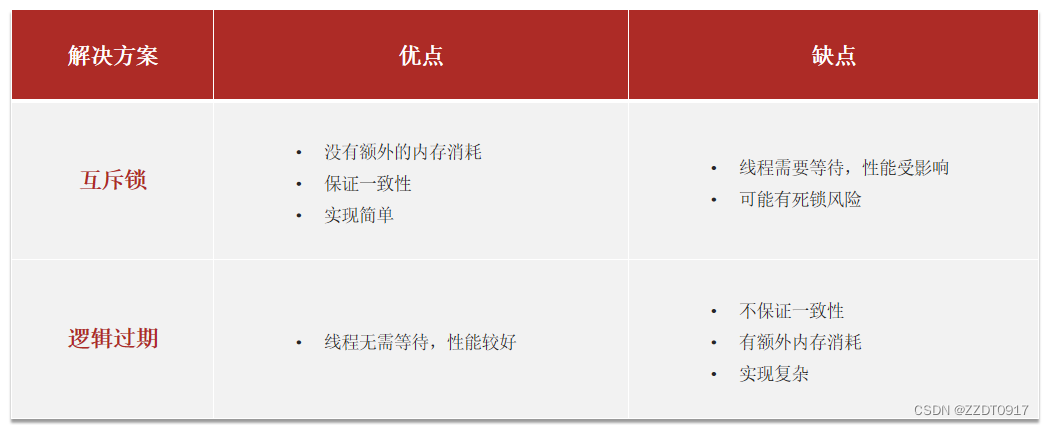
黑马redis学习记录:缓存
一、介绍 什么是缓存? 缓存(Cache),就是数据交换的缓冲区,俗称的缓存就是缓冲区内的数据,一般从数据库中获取,存储于本地代码 缓存无处不在 为什么要使用缓存? 因为速度快,好用缓存数据存储于代码中,而…...
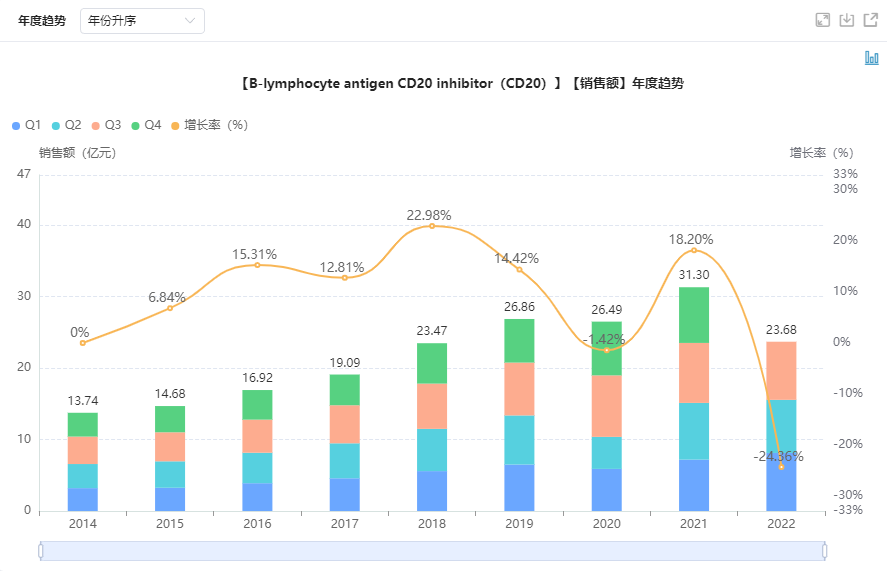
CD20靶向药物|适应症|市场销售-上市药品前景分析
CD20是靶向治疗的第一个靶点,是B细胞淋巴瘤的现代治疗药物。CD20作为治疗剂的使用被认为是方便的,原因有二。首先,在 CD20 阳性肿瘤的情况下,这种受体大量存在于 B 淋巴细胞表面——每个细胞大约有十万个分子。其次,干…...

多源 复制
使复制从属服务器能够同时从多个主服务器接收事务至少需要两个主服务器和一个从属服务器设备从属服务器为每个主服务器创建一个 复制通道从属服务器必须使用基于表的资料档案库多源复制与基于文件的资料档案库不兼容不尝试检测或解决冲突如果需要此功能,则由应用程序…...
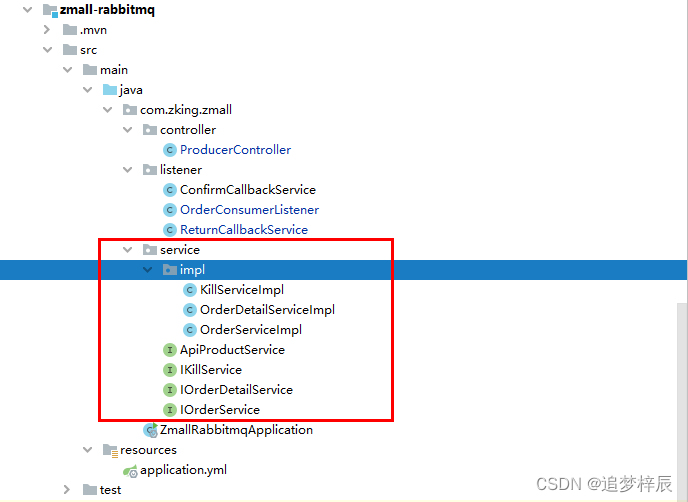
微服务项目【消息推送(RabbitMQ)】
创建消费者 第1步:基于Spring Initialzr方式创建zmall-rabbitmq消费者模块 第2步:在公共模块中添加rabbitmq相关依赖 <!--rabbitmq--> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-bo…...

vr电力刀闸事故应急演练实训系统开发
电力事故是在电力生产和输电过程中可能发生的意外事件,它们可能会对人们的生命财产安全造成严重的威胁。因此,电力事故应急演练显得尤为重要。而VR技术则可以为电力事故应急演练提供一种全新的解决方案。 在虚拟环境中,元宇宙VR会模拟各种触电…...
C++类和对象补充
目录 前言: 1. 构造函数->初始化列表 1.1 初始化列表出现原因 1.2 初始化列表写法 2. explicit关键字 2.1 explict的出现 2.2 explict的写法 3. static成员 4. 友元 4.1 友元函数 4.2 友元类 5. 内部类和匿名对象 5.1 内部类 5.2 匿名对象 前言&a…...
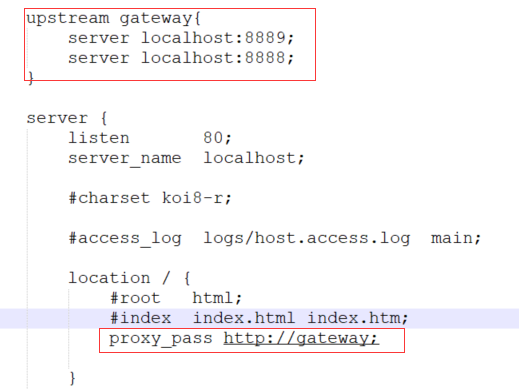
08 SpringCloud 微服务网关Gateway组件
网关简介 大家都都知道在微服务架构中,一个系统会被拆分为很多个微服务。那么作为客户端要如何去调用这么多的微服务呢? 如果没有网关的存在,我们只能在客户端记录每个微服务的地址,然后分别去用。 这样的架构,会存…...
极验3代 加密分析
目标链接 aHR0cHM6Ly93d3cuZ2VldGVzdC5jb20vZGVtby9zbGlkZS1mbG9hdC5odG1s接口分析 极验参数重要信息 gt和challenge;gt是固定的,但是challenge每次请求会产生不同的,这里的请求的并没有什么加密参数。 下一个请求 gettype.php,…...

python 数据分析可视化实战 超全 附完整代码数据
代码数据:https://download.csdn.net/download/qq_38735017/873799141.1 数据预处理1.1.1 异常值检测①将支付时间转为标准时间的过程中发生错误,经排查错误数据为‘2017/2/29’,后将其修改为‘2017/2/27’。②经检测发现部分订单应付金额与实付金额都为…...
有趣的HTML实例(十三) 咖啡选择(css+js)
一个人追求目标的路途是孤单的,一个人独品辛酸的时候是寂寥的,一个人马不停蹄的追赶着,狂奔着,相信前方是一片光明,我从不放弃希望,就像我对生活的信念,没有人可以动摇。 ——《北京青年》 目录…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
