代码随想录算法训练营第三十天 | 单调栈系列复习
单调栈系列复习
- 每日温度
- 未看解答自己编写的青春版
- 重点
- 题解的代码
- 日后再次复习重新写
- 下一个更大元素 I
- 未看解答自己编写的青春版
- 重点
- 题解的代码
- 日后再次复习重新写
- 下一个更大元素II
- 未看解答自己编写的青春版
- 重点
- 题解的代码
- 日后再次复习重新写
- 接雨水
- 未看解答自己编写的青春版
- 重点
- 题解的代码
- 按题解风格重写
- 日后再次复习重新写
- 柱状图中最大的矩形
- 未看解答自己编写的青春版
- 本题计算矩形面积的方式:依旧按照上一题接雨水的思路,采取横向计算的方式!对于当前遍历的位置 i ,取当前位置的高度为合并矩形的高度,向左向右遍历,找到左右两边第一个比此高度底的位置,面积就等于高X宽。
- 卡哥的双指针法竟然不超时?为什么
- 明白了,在循环找左右临近最小时,不需要一个下标一个下标地去遍历,可以利用已经算好的值进行跳跃!!!
- 这道题因为必须横向计算面积,没有列向计算的方法,所以我认为,没有像上一题,接雨水那样,具有显著风格的双指针方法。
- 单调栈方法,这道题因为要求左右最小临近,所以是递减栈。
- 这道题的边界情况不好处理我觉得,左边的情况可以通过while里加判断解决。右边的情况,目前我认为只能在for循环结束后,单独再去弹出栈来计算了。我感觉不如对heights数组,左右加0。看看卡哥的写法
- 重点
- 题解的代码
- 啊哈,也是通过前后补0做的,合理。
- 日后再次复习重新写
- 一段用于复制的标题
- 未看解答自己编写的青春版
- 重点
- 题解的代码
- 日后再次复习重新写
- 一段用于复制的标题
- 未看解答自己编写的青春版
- 重点
- 题解的代码
- 日后再次复习重新写
- 一段用于复制的标题
- 未看解答自己编写的青春版
- 重点
- 题解的代码
- 日后再次复习重新写
每日温度
未看解答自己编写的青春版
class Solution:def dailyTemperatures(self, temperatures: List[int]) -> List[int]:n = len(temperatures)stack = [0]res = [0]*nfor i in range(1,n):while stack != [] and temperatures[i] > temperatures[stack[-1]] :idx = stack.pop()res[idx] = i-idxstack.append(i)return res
重点
每日温度
1、对比用while
2、单调栈里存下标即可
3、求右边第一个更大,所以是单调递增栈,指的是:从栈顶到栈底,顺序是单增,栈顶是弹出和加入元素的位置。
题解的代码
日后再次复习重新写
下一个更大元素 I
未看解答自己编写的青春版
class Solution:def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:n = len(nums2)res = [-1]*n# stack还是得存下标,存数,不方便索引到res结果数组stack = [0]for i in range(1,n):while stack != [] and nums2[i] > nums2[stack[-1]] :idx = stack.pop()res[idx] = nums2[i]stack.append(i)m = len(nums1)result = [-1]*mfor i in range(m):temp = nums2.index(nums1[i])result[i] = res[temp]return result
重点
同上一题。找索引用 list.index()
下一个更大元素 I
题解的代码
日后再次复习重新写
下一个更大元素II
未看解答自己编写的青春版
class Solution:def nextGreaterElements(self, nums: List[int]) -> List[int]:n = len(nums)res = [-1]*nstack = [0]for i in range(1,2*n):temp = i % nwhile stack != [] and nums[temp] > nums[stack[-1]] :j = stack.pop()# 注意看,我们对每个进入stack,单调栈的元素,都做了对n的取模处理# 所以这里pop出来的 j ,一定是好的,不需要经过处理就可以对结果数组赋值res[j] = nums[temp]stack.append(temp)return res重点
本题需要处理的就是,循环数组,的情况。
朴实的想法是:把目标数组复制一倍,将目标数组扩容为两倍,然后对这个两倍的数组做最原始的单调栈。
可以进一步优化:在索引循环时,循环到 2*n , 但是对于每个 i ,对 i 进行对数组长度 n 的取模操作。
题解的代码
日后再次复习重新写
接雨水
未看解答自己编写的青春版
class Solution:def trap(self, height: List[int]) -> int:total = 0n = len(height)# 栈里放的是索引stack = [0]for i in range(1,n): temp = 0while stack != [] and height[i] > 0 and height[i] >= height[stack[-1]] :j = stack.pop()total += (height[j]-temp)*(i-j-1)temp = height[j]# 这个判断是为了处理,中间有矮柱,或者空的情况,但是是我根据错误示例发现的,没什么道理啊# 简单举例为:[4,2,1,3] [4,0,0,3] 不加下面的判断,就会漏掉4和3之间的部分if stack != [] and height[i] < height[stack[-1]] :total += (height[i]-temp)*(i-stack[-1]-1)if height[i] > 0 :stack.append(i)return total
重点
这题要看题解,自己写的代码中,加入的一段逻辑,是为了AC而加的,如果不是题目有错误示例,我想不到。
接雨水
还是觉得,卡哥的题解给的方法是自然的,按我的方法,第一次确实想不到这种要单独处理的情况。而且不让0入栈,是比较牵强的。
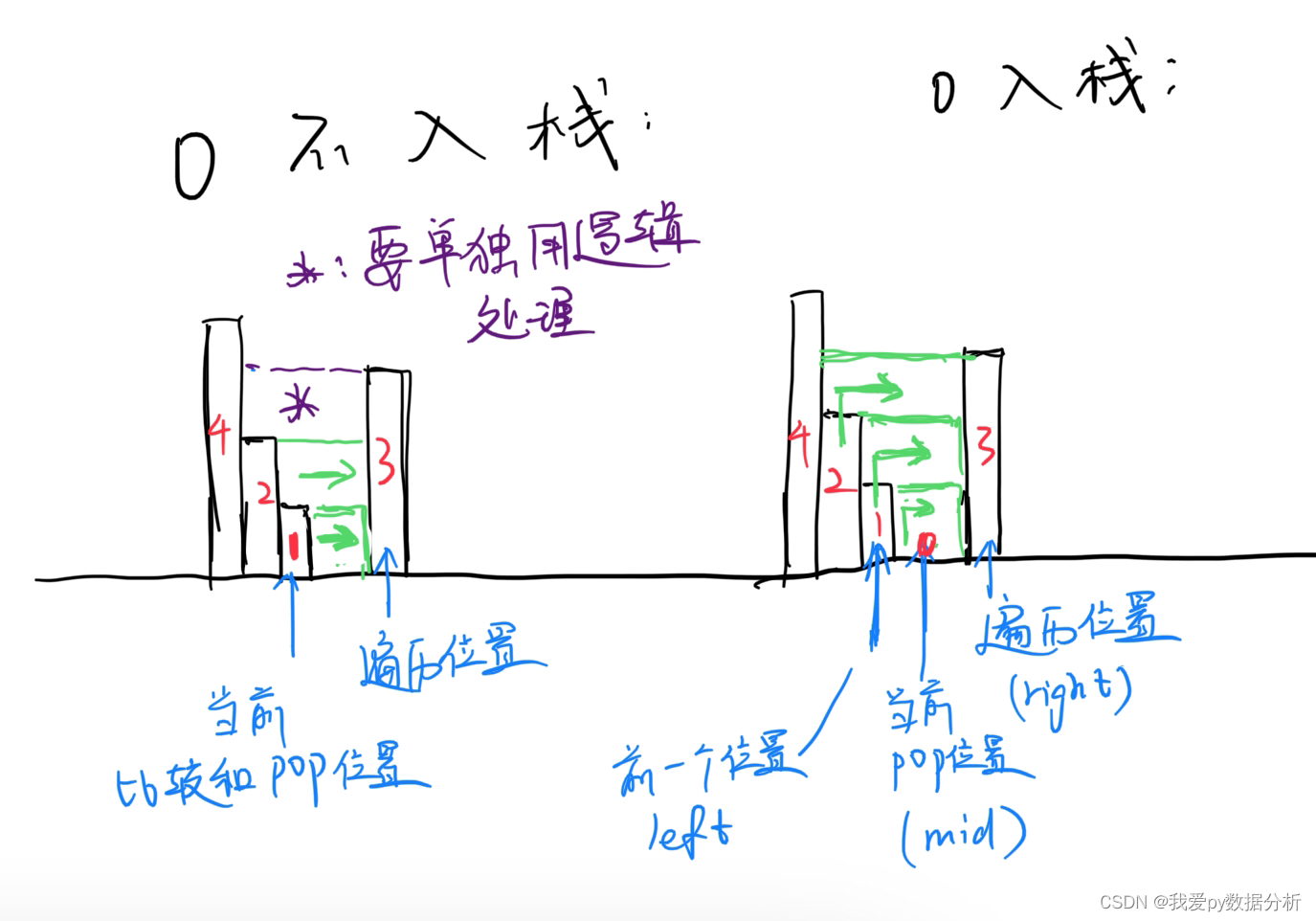
本题还有一个要注意的是:如果两个数值相等,怎么处理?照常入栈,顶替掉前一个!
题解的代码
class Solution:def trap(self, height: List[int]) -> int:# 单调栈'''单调栈是按照 行 的方向来计算雨水从栈顶到栈底的顺序:从小到大通过三个元素来接水:栈顶,栈顶的下一个元素,以及即将入栈的元素雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1(因为只求中间宽度)'''# stack储存index,用于计算对应的柱子高度stack = [0]result = 0for i in range(1, len(height)):# 情况一if height[i] < height[stack[-1]]:stack.append(i)# 情况二# 当当前柱子高度和栈顶一致时,左边的一个是不可能存放雨水的,所以保留右侧新柱子# 需要使用最右边的柱子来计算宽度elif height[i] == height[stack[-1]]:stack.pop()stack.append(i)# 情况三else:# 抛出所有较低的柱子while stack and height[i] > height[stack[-1]]:# 栈顶就是中间的柱子:储水槽,就是凹槽的地步mid_height = height[stack[-1]]stack.pop()if stack:right_height = height[i]left_height = height[stack[-1]]# 两侧的较矮一方的高度 - 凹槽底部高度h = min(right_height, left_height) - mid_height# 凹槽右侧下标 - 凹槽左侧下标 - 1: 只求中间宽度w = i - stack[-1] - 1# 体积:高乘宽result += h * wstack.append(i)return result# 单调栈压缩版
class Solution:def trap(self, height: List[int]) -> int:stack = [0]result = 0for i in range(1, len(height)):while stack and height[i] > height[stack[-1]]:mid_height = stack.pop()if stack:# 雨水高度是 min(凹槽左侧高度, 凹槽右侧高度) - 凹槽底部高度h = min(height[stack[-1]], height[i]) - height[mid_height]# 雨水宽度是 凹槽右侧的下标 - 凹槽左侧的下标 - 1w = i - stack[-1] - 1# 累计总雨水体积result += h * wstack.append(i)return result
按题解风格重写
class Solution:def trap(self, height: List[int]) -> int:total = 0n = len(height)# 栈里放的是索引stack = [0]for i in range(1,n): while stack != [] and height[i] >= height[stack[-1]] :mid = stack.pop()if stack != []:left = stack[-1]total += (min(height[left],height[i])-height[mid])*(i-left-1)stack.append(i)return total
日后再次复习重新写
柱状图中最大的矩形
未看解答自己编写的青春版
没有思路,主要难点在于,不知道怎样计算最大矩形面积合适。包括上一道题一样,一开始也是不晓得怎样计算雨水面积合适(比如上一道题,按照单调栈计算,是按照行来计算的)。
本题计算矩形面积的方式:依旧按照上一题接雨水的思路,采取横向计算的方式!对于当前遍历的位置 i ,取当前位置的高度为合并矩形的高度,向左向右遍历,找到左右两边第一个比此高度底的位置,面积就等于高X宽。
单调栈没思路的时候,先用暴力解法试试。
暴力法:超时
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:maxarea = 0n = len(heights)for i in range(n):h = heights[i]left = i-1right = i+1while left > -1 :if heights[left] < heights[i] :breakleft -= 1while right < n :if heights[right] < heights[i] :breakright += 1temp = h * (right-left-1)maxarea = max(maxarea,temp)return maxarea
DP法(二维数组提前存储每个位置的第一个左边小于当前高度的下标,第一个右边小于当前高度的下标)。超时。(在本题中,DP法和双指针法相同了,DP也无法用递推公式,都是用两个一维数组去提前存储,而且都需要循环去搜索。)
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:maxarea = 0n = len(heights)dp = [[0]*2 for _ in range(n)]dp[0][0] = -1dp[n-1][1] = n# 注意本题与前一题接雨水的不同,前一题因为在用暴力法(DP,双指针)都是采用列向计算# 所以在计算左右临近最大时,可以使用迭代# 本题因为是求左右临近最小,用提前记忆的方法,依然需要循环!for i in range(1,n):j = iwhile j > 0 and heights[i] <= heights[j-1]:j = j-1dp[i][0] = j-1for i in range(n-2,-1,-1):j = iwhile j < n-1 and heights[i] <= heights[j+1]:j = j+1dp[i][1] = j+1for i in range(n):h = heights[i]left = dp[i][0]right = dp[i][1] temp = h * (right-left-1)maxarea = max(maxarea,temp)return maxarea 卡哥的双指针法竟然不超时?为什么
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:size = len(heights)# 两个DP数列储存的均是下标indexmin_left_index = [0] * sizemin_right_index = [0] * sizeresult = 0# 记录每个柱子的左侧第一个矮一级的柱子的下标min_left_index[0] = -1 # 初始化防止while死循环for i in range(1, size):# 以当前柱子为主心骨,向左迭代寻找次级柱子temp = i - 1while temp >= 0 and heights[temp] >= heights[i]:# 当左侧的柱子持续较高时,尝试这个高柱子自己的次级柱子(DPtemp = min_left_index[temp]# 当找到左侧矮一级的目标柱子时min_left_index[i] = temp# 记录每个柱子的右侧第一个矮一级的柱子的下标min_right_index[size-1] = size # 初始化防止while死循环for i in range(size-2, -1, -1):# 以当前柱子为主心骨,向右迭代寻找次级柱子temp = i + 1while temp < size and heights[temp] >= heights[i]:# 当右侧的柱子持续较高时,尝试这个高柱子自己的次级柱子(DPtemp = min_right_index[temp]# 当找到右侧矮一级的目标柱子时min_right_index[i] = tempfor i in range(size):area = heights[i] * (min_right_index[i] - min_left_index[i] - 1)result = max(area, result)return result
明白了,在循环找左右临近最小时,不需要一个下标一个下标地去遍历,可以利用已经算好的值进行跳跃!!!
在上面原代码的基础上进行的修改,但是由于上面那一版没想到这些,用的下标是和 j-1 / j+1 比较的,简直是下标灾难!
这个代码能过,但是时间和空间上只打败了 5% 。
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:maxarea = 0n = len(heights)dp = [[0]*2 for _ in range(n)]dp[0][0] = -1dp[n-1][1] = n# 注意本题与前一题接雨水的不同,前一题因为在用暴力法(DP,双指针)都是采用列向计算# 所以在计算左右临近最大时,可以使用迭代# 本题因为是求左右临近最小,用提前记忆的方法,依然需要循环!for i in range(1,n):j = i# 下标灾难while j > 0 and heights[i] <= heights[j-1]:# index要减一,dp出来的值要加一,因为上面的判断,是和减一的位置判断的j = dp[j-1][0]+1dp[i][0] = j-1for i in range(n-2,-1,-1):j = iwhile j < n-1 and heights[i] <= heights[j+1]:# index要加一,dp出来的值要减一,因为上面的判断,是和加一的位置判断的j = dp[j+1][1]-1dp[i][1] = j+1for i in range(n):h = heights[i]left = dp[i][0]right = dp[i][1] temp = h * (right-left-1)maxarea = max(maxarea,temp)return maxarea
不用该死的 j-1 / j+1 了,重新更改下标!
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:maxarea = 0n = len(heights)dp = [[0]*2 for _ in range(n)]dp[0][0] = -1dp[n-1][1] = n# 注意本题与前一题接雨水的不同,前一题因为在用暴力法(DP,双指针)都是采用列向计算# 所以在计算左右临近最大时,可以使用迭代# 本题因为是求左右临近最小,用提前记忆的方法,依然需要循环!for i in range(1,n):j = i-1while j > -1 and heights[i] <= heights[j]: j = dp[j][0]dp[i][0] = jfor i in range(n-2,-1,-1):j = i+1while j < n and heights[i] <= heights[j]: j = dp[j][1]dp[i][1] = jfor i in range(n):h = heights[i]left = dp[i][0]right = dp[i][1] temp = h * (right-left-1)maxarea = max(maxarea,temp)return maxarea
更改后,下标看起来顺眼多了,但是还是都只打败了5%,why ?
将二维dp数组,拆为了两个一维数组。
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:maxarea = 0n = len(heights)# 初始化一起做了dp1 = [-1]*ndp2 = [n]*n# 注意本题与前一题接雨水的不同,前一题因为在用暴力法(DP,双指针)都是采用列向计算# 所以在计算左右临近最大时,可以使用迭代# 本题因为是求左右临近最小,用提前记忆的方法,依然需要循环!for i in range(1,n):j = i-1while j > -1 and heights[i] <= heights[j]: j = dp1[j]dp1[i] = jfor i in range(n-2,-1,-1):j = i+1while j < n and heights[i] <= heights[j]: j = dp2[j]dp2[i] = jfor i in range(n):h = heights[i]left = dp1[i]right = dp2[i]temp = h * (right-left-1)maxarea = max(maxarea,temp)return maxarea
啪的一下,很快啊,就打败40%了!
这道题因为必须横向计算面积,没有列向计算的方法,所以我认为,没有像上一题,接雨水那样,具有显著风格的双指针方法。
单调栈方法,这道题因为要求左右最小临近,所以是递减栈。
这道题的边界情况不好处理我觉得,左边的情况可以通过while里加判断解决。右边的情况,目前我认为只能在for循环结束后,单独再去弹出栈来计算了。我感觉不如对heights数组,左右加0。看看卡哥的写法
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:maxarea = 0# 这道题的边界情况不好处理我觉得,左边的情况可以通过while里加判断解决# 右边的情况,目前我认为只能在for循环结束后,单独再去弹出栈来计算了# 我感觉不如对heights数组,左右加0heights = [0]+heights+[0]n = len(heights)stack = [0]for i in range(1,n):while stack != [] and heights[i] < heights[stack[-1]]:temp = stack.pop()if stack != [] :left = stack[-1]j = heights[temp]*(i-left-1)maxarea = max(maxarea,j)stack.append(i)return maxarea
重点
接雨水 (opens new window)是找每个柱子左右两边第一个大于该柱子高度的柱子,而本题是找每个柱子左右两边第一个小于该柱子的柱子。
这里就涉及到了单调栈很重要的性质,就是单调栈里的顺序,是从小到大还是从大到小。
在接雨水 (opens new window)中,单调栈从栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序。
因为本题是要找每个柱子左右两边第一个小于该柱子的柱子,所以从栈头(元素从栈头弹出)到栈底的顺序应该是从大到小的顺序。
题解的代码
啊哈,也是通过前后补0做的,合理。
# 单调栈
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:# Monotonic Stack'''找每个柱子左右侧的第一个高度值小于该柱子的柱子单调栈:栈顶到栈底:从大到小(每插入一个新的小数值时,都要弹出先前的大数值)栈顶,栈顶的下一个元素,即将入栈的元素:这三个元素组成了最大面积的高度和宽度情况一:当前遍历的元素heights[i]大于栈顶元素的情况情况二:当前遍历的元素heights[i]等于栈顶元素的情况情况三:当前遍历的元素heights[i]小于栈顶元素的情况'''# 输入数组首尾各补上一个0(与42.接雨水不同的是,本题原首尾的两个柱子可以作为核心柱进行最大面积尝试heights.insert(0, 0)heights.append(0)stack = [0]result = 0for i in range(1, len(heights)):# 情况一if heights[i] > heights[stack[-1]]:stack.append(i)# 情况二elif heights[i] == heights[stack[-1]]:stack.pop()stack.append(i)# 情况三else:# 抛出所有较高的柱子while stack and heights[i] < heights[stack[-1]]:# 栈顶就是中间的柱子,主心骨mid_index = stack[-1]stack.pop()if stack:left_index = stack[-1]right_index = iwidth = right_index - left_index - 1height = heights[mid_index]result = max(result, width * height)stack.append(i)return result# 单调栈精简
class Solution:def largestRectangleArea(self, heights: List[int]) -> int:heights.insert(0, 0)heights.append(0)stack = [0]result = 0for i in range(1, len(heights)):while stack and heights[i] < heights[stack[-1]]:mid_height = heights[stack[-1]]stack.pop()if stack:# area = width * heightarea = (i - stack[-1] - 1) * mid_heightresult = max(area, result)stack.append(i)return result日后再次复习重新写
一段用于复制的标题
未看解答自己编写的青春版
重点
题解的代码
日后再次复习重新写
一段用于复制的标题
未看解答自己编写的青春版
重点
题解的代码
日后再次复习重新写
一段用于复制的标题
未看解答自己编写的青春版
重点
题解的代码
日后再次复习重新写
相关文章:

代码随想录算法训练营第三十天 | 单调栈系列复习
单调栈系列复习 每日温度未看解答自己编写的青春版重点题解的代码日后再次复习重新写 下一个更大元素 I未看解答自己编写的青春版重点题解的代码日后再次复习重新写 下一个更大元素II未看解答自己编写的青春版重点题解的代码日后再次复习重新写 接雨水未看解答自己编写的青春版…...

redis数据未到过期时间被删除
1. 问题描述 使用了jeecgboot开发后端代码,代码设置的redis过期时间为24小时,部署使用的宝塔面板,在redis中看到的过期时间也是为24小时,但是并未到过期时间,数据就被删除。 2. 解决办法 观察了一下redis中的数据&a…...

32.选择器
选择器 html部分 <div class"toggle-container"><input type"checkbox" id"good" class"toggle"><label for"good" class"label"><div class"ball"></div></label&…...

Linux--验证命令行上运行的程序的父进程是bash
1.输入以下代码: #include <stdio.h> #include <unistd.h> int main() {printf("hello world: pid: %d, ppid: %d\n",getpid(),getppid());return 0; }2.编译得到可执行程序 3.运行得到ppid 4.输入指令 ps axj | head -1 &&am…...
MySQL数据库关于表的一系列操作
MySQL中的数据类型 varchar 动态字符串类型(最长255位),可以根据实际长度来动态分配空间,例如:varchar(100) char 定长字符串(最长255位),存储空间是固定的,例如&#…...

Spring基于注解管理bean及全注解开发
文章目录 spring概述Spring定义Spring核心Spring Framework的特点 基于注解管理bean依赖开启组件扫描使用注解定义Bean案例:Autowired注入属性注入set注入形参上注入只有一个构造函数,无注解Autowire注解和Qualifier注解联合 Resource注入Spring全注解开发 spring概…...
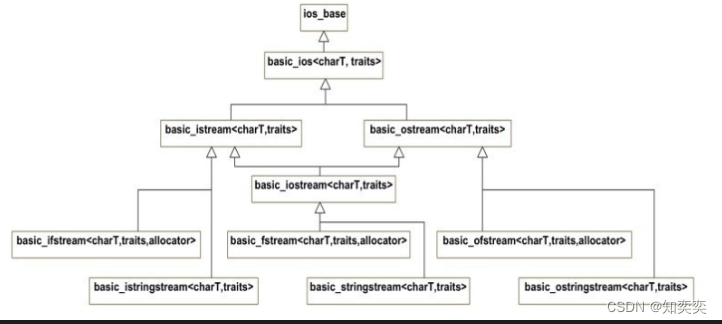
QtC++ 技术分析3 - IOStream
目录 iostreamscanf/printfiostream 整体架构流相关类流缓冲区 模板特化后整体结构文件流文件流对象创建常见文件流操作输出格式设定文件流状态 字符串流字符串流内部缓冲区字符串流使用 流缓冲区用户自定义 IO iostream scanf/printf 几种常见的输入输出流函数 scanf 从键盘…...
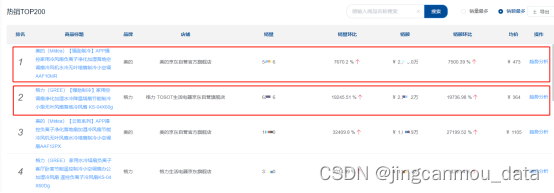
2023年Q2京东环境电器市场数据分析(京东数据产品)
今年Q2,环境电器市场中不少类目表现亮眼,尤其是以净水器、空气净化器、除湿机等为代表的环境健康电器。此外,像冷风扇这类具有强季节性特征的电器也呈现出比较好的增长态势。 接下来,结合具体数据我们一起来分析Q2环境电器市场中…...
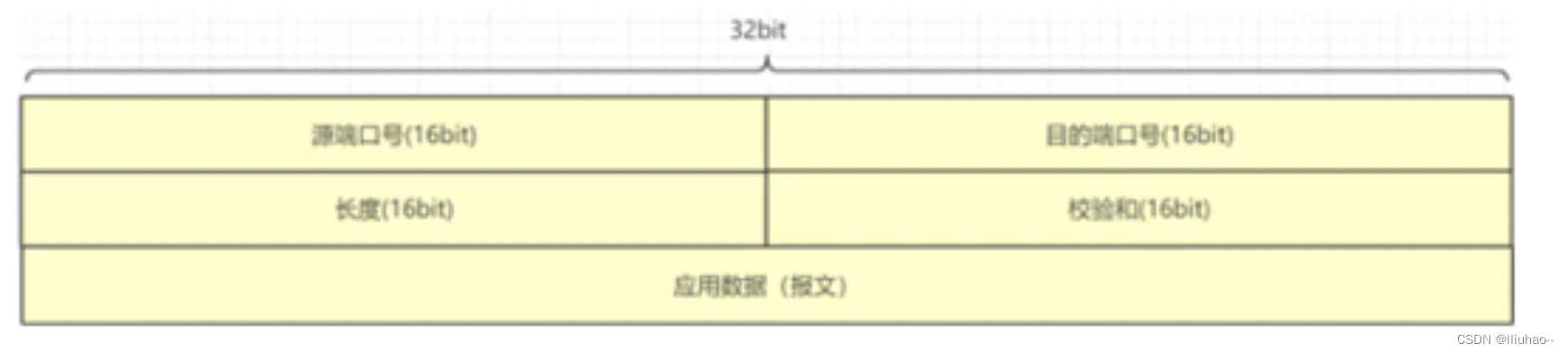
TCP/UDP的首部
TCP/UDP首部信息 TCP首部第一个4字节第二个4字节与第三个4字节第四个4字节第五个4字节选项最大报文段长度(MSS)选项窗口扩大选项时间戳选项 什么时候发送RST包UDP首部 TCP首部 TCP 首部长度为20字节,加上选项部分最大可达60字节。 第一个4…...
从入门到精通系列之四:K8s的基本概念和术语之集群类)
Kubernetes(K8s)从入门到精通系列之四:K8s的基本概念和术语之集群类
Kubernetes K8s从入门到精通系列之四:K8s的基本概念和术语之集群类 一、Master二、Node三、命名空间集群表示一个由Master和Node组成的K8s集群。 一、Master Master指的是集群的控制节点。在每个K8s集群都需要有一个或一组被称为Master的节点,来负责整个集群的管理和控制。M…...
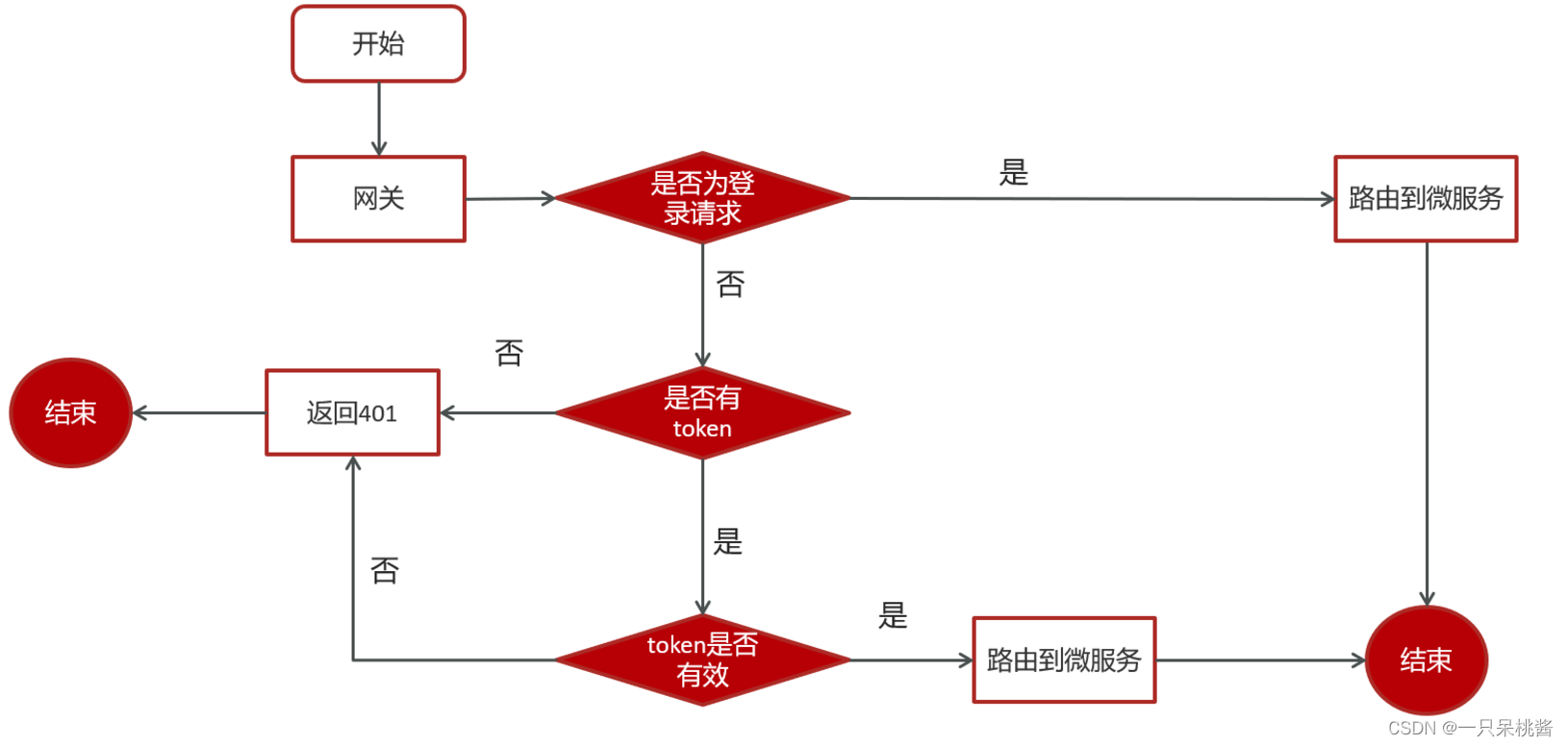
黑马头条---day1
手机端查看 docker 容器,镜像操作命令 1、docker删除所有镜像命令 删除所有镜像的命令是Docker中一个非常常见的操作。下面是具体的实现步骤和命令示例: $ docker stop $(docker ps -aq) 停止所有正在运行的容器。 $ docker rm $(docker ps -aq) 删…...

【序列化工具JdkSerialize和Protostuff】
序列化工具对比 JdkSerialize:java内置的序列化能将实现了Serilazable接口的对象进行序列化和反序列化, ObjectOutputStream的writeObject()方法可序列化对象生成字节数组 Protostuff:google开源的protostuff采用更为紧凑的二进制数组&#…...

C++ 多线程编程导论(下)
文章目录 参考资料线程安全(续)门闩与屏障——latch 对象与 barrier 对象门闩(latch)屏障(barrier) 一次性调用——once_flag 对象与 call_once 函数 异步任务未来与承诺——future 对象与 promise 对象fut…...
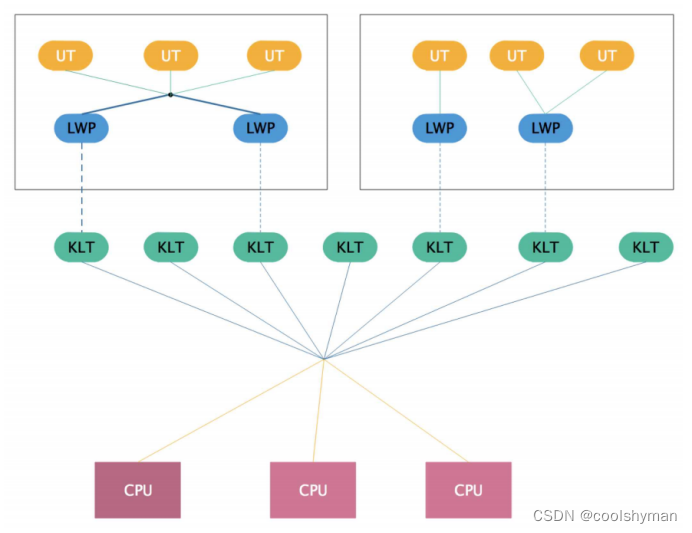
Java并发系列之一:JVM线程模型
什么是线程模型: Java字节码运行在JVM中,JVM运行在各个操作系统上。所以当JVM想要进行线程创建回收这种操作时,势必需要调用操作系统的相关接口。也就是说,JVM线程与操作系统线程之间存在着某种映射关系,这两种不同维…...

容灾独家技术揭秘:HyperBDR无主机数据同步技术
01、一对一单机热备-传统灾备方式 单机热备是一种备份解决方案,它使用两台服务器来确保高可用性,是市场上最为常见的灾备模式。 在单机热备中,一台主服务器和一台备用服务器保持同步,以确保在主服务器出现故障或宕机时可以立即切换…...

FANUC机器人SRVO-050碰撞检测报警和SRVO-053干扰值过大故障报警总结
FANUC机器人SRVO-050碰撞检测报警和SRVO-053干扰值过大故障报警总结 前面和大家分享了关于SRVO-050碰撞检测报警和SRVO-053干扰值过大的原因分析以及处理方法,感兴趣的朋友可以参考以下链接中的内容: FANUC机器人SRVO-050碰撞检测报警原因分析及处理对策...
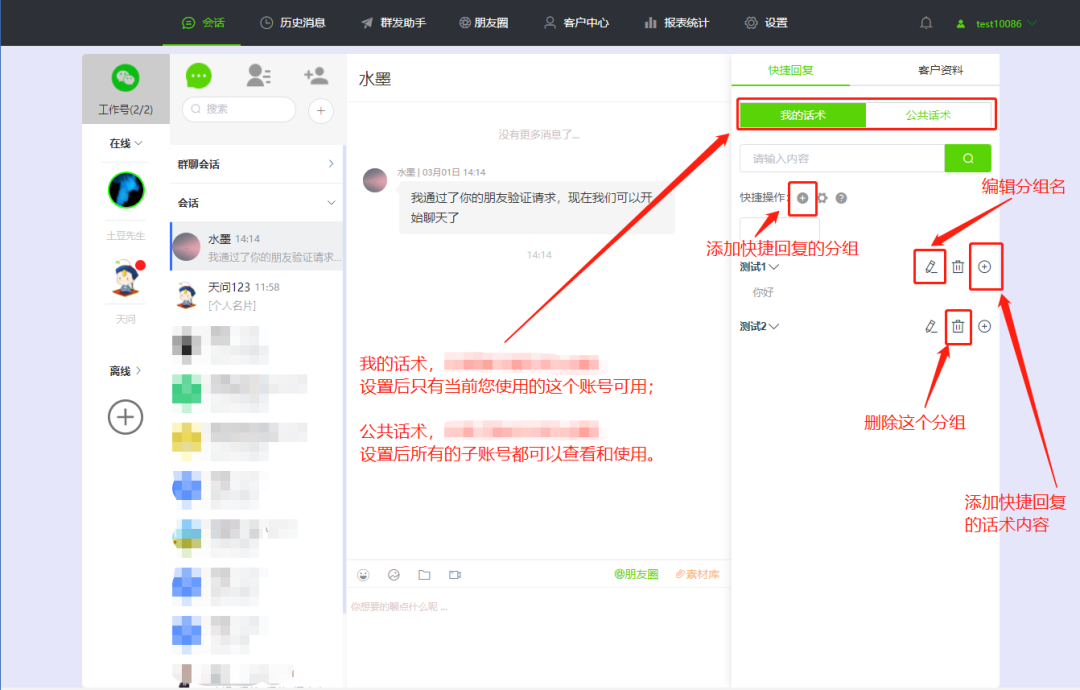
微信如何提高回复信息速度?
规范流程话术有什么用?为了提高回复客户的效率和质量,可以事先设计好的一套标准化的对话模板。它通常包括多个环节和问题,帮助客服人员或销售人员在与客户沟通时,按照标准化的流程进行,以提高工作效率和客户满意度。 如…...
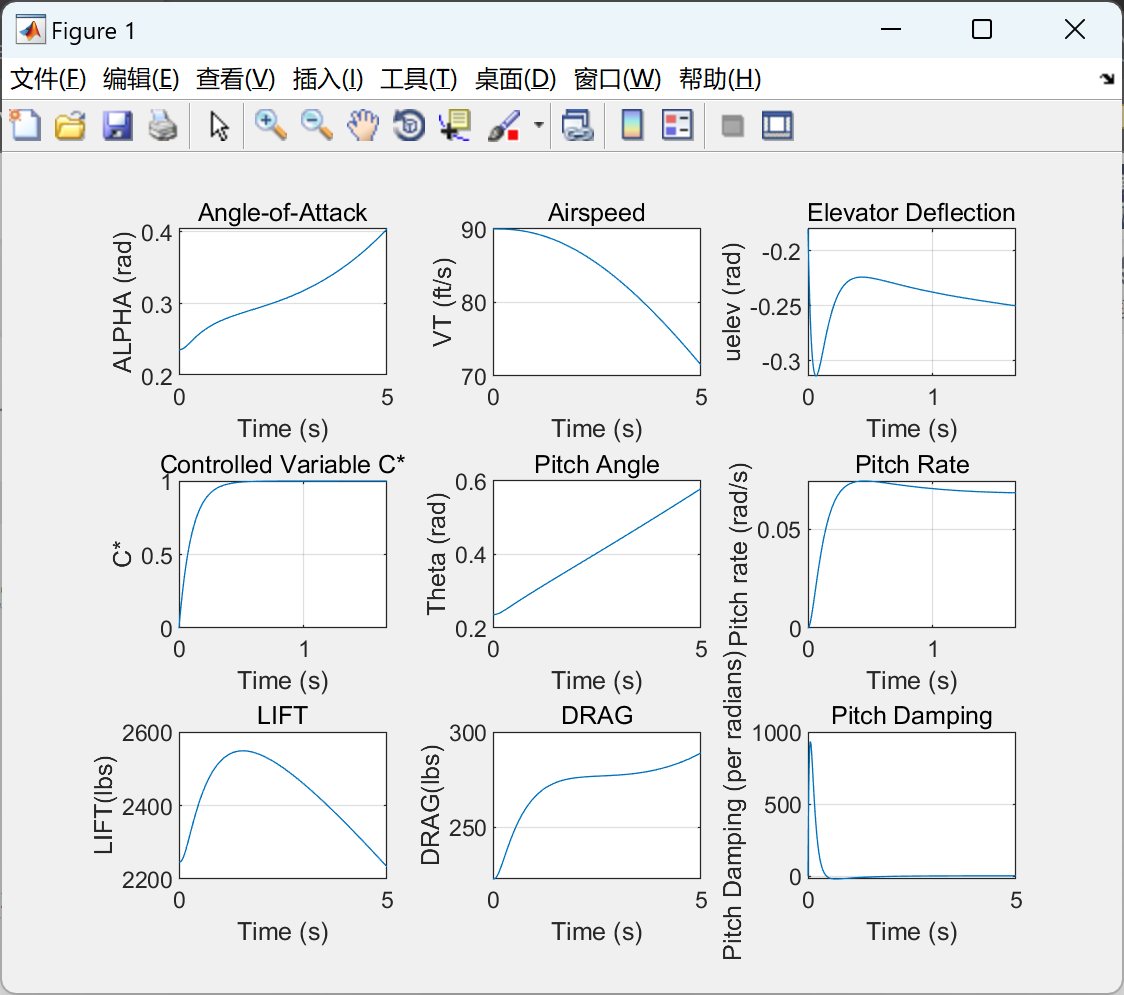
模拟Stevens Lewis描述的小型飞机纵向动力学的非线性动态反演控制器研究(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 🌈4 Matlab代码实现 💥1 概述 针对Stevens和Lewis描述的小型飞机纵向动力学的非线性动态,研究非线性动态反演控制器可以是一个有趣的课题。动态反演控制器的目标…...
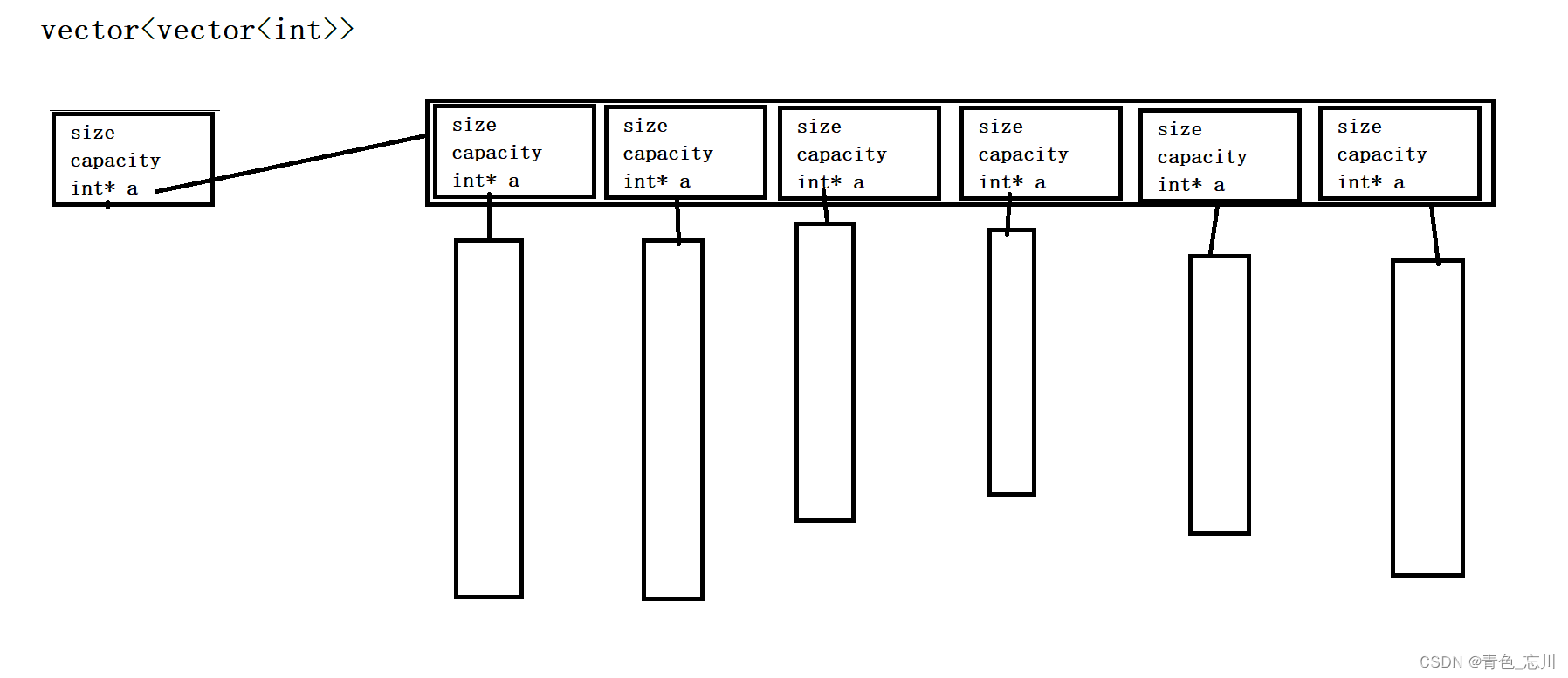
【C++从0到王者】第十二站:vector基本使用
文章目录 一、vector基本介绍二、vector的基本使用三、vector\<char> 和string的区别四、vector接口介绍1.vector的模板参数2.构造函数3.迭代器4.size和max_size5.resize和reserve6.operator[]和at7.front和back8.data9.push_back和pop_back10.insert和erase11.assign12.…...
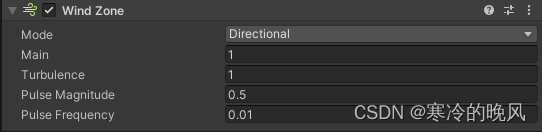
了解Unity编辑器之组件篇Miscellaneous(九)
一、Aim Constraint:是一种动画约束,用于使一个对象朝向另一个对象或一个指定的矢量方向 Activate按钮:用于激活或停用Aim Constraint。当Aim Constraint处于激活状态时,其约束效果将应用于目标对象。 Zero按钮:用于将…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...
