(文章复现)梯级水光互补系统最大化可消纳电量期望短期优化调度模型matlab代码
参考文献:
[1]罗彬,陈永灿,刘昭伟等.梯级水光互补系统最大化可消纳电量期望短期优化调度模型[J].电力系统自动化,2023,47(10):66-75.
1.基本原理
1.1 目标函数
考虑光伏出力的不确定性,以梯级水光互补系统的可消纳电量期望最大为目标,函数可表示为:


1.2约束条件
1.2.1 电站约束
1)水量平衡约束

2)水库水位约束
 3)初始水位和末水位控制
3)初始水位和末水位控制
 4)出库流量约束
4)出库流量约束
 5)电站出力约束
5)电站出力约束
 6)水位-库容关系
6)水位-库容关系
![]()
 7)尾水位-泄流量关系
7)尾水位-泄流量关系

1.2.2 机组约束
1)机组出力约束
 2)机组发电流量约束
2)机组发电流量约束
 3)机组振动区约束
3)机组振动区约束
 4)机组开、停机持续时间约束
4)机组开、停机持续时间约束

机组在调度期内的最大开机次数,以避免频繁开停机。
5)机组出力爬坡约束
 6)机组出力波动限制约束
6)机组出力波动限制约束
 7)机组发电水头约束
7)机组发电水头约束
 8)水头损失函数
8)水头损失函数

9)机组动力特性关系

1.2.3 电网约束
1)梯级水电出力范围约束
 2)分区断面约束
2)分区断面约束

从目标函数和分区断面约束可以看出,弃电量中未设置弃水、弃光的优先级,模型目标会使得梯级水电在允许出力范围内优先蓄水减发,以提升受阻断面内光伏消纳量,从而提升互补系统整体可消纳水平,但为保障电网供电支撑无法继续减发时,受到分区断面限制而造成弃光也不可避免。
2.模型求解
2.1 模型转换
MILP模型构建的关键在于模型的线性化转换 ,所提模型非线性约束包括式(10)、式(11)、式(16)、式(19)、式(21)和式(22)。其中,水位-库容、尾水位-泄流量以及水头损失函数可采用分段线性的方式进行处理[22]。 机组的动力特性参考文献[26],采用三角形权值技术进行处理。特殊地,对于季调节及以上电站,日内始末水位变化幅度较小,可在初始水位附近采用线性函数表示水位库容关系。
1)机组振动区约束线性化
大型机组可能存在多个振动区,将出力在最大最小出力范围内划分为多个非连续的安全运行区间。借鉴文献[21],文中假设机组振动区不随机组水头变化而改变,即固定的振动区,假设机组有 K 个振动区,则有 K + 1 个安全运行区间,即

2)水电机组出力波动限制约束线性化
水电机组出力的频繁波动表现为相邻时段出力的向上或向下调节。区别于已有文献中采用的关联搜索[27] 和负荷重构[28] 等方法,文中创新性地通过引入调节指标变量进行处理,可有效提高求解效率。


因此 ,式(19)的非线性约束可用式(29)—式(31)替代。如图1所示机组状态变化示意图,当机组稳定出力时间达到 te 后,机组具有上调、下调和平稳出力 3 种有效状态,假设此时为 t0 时刻,若 t1 时刻上调或下调出力,调整之后则仅有平稳出力状态有效,上调和下调的状态暂时无效,直到稳定出力时间再次达到 te 后,机组上调和下调的状态重新有效,如此逐时段约束保证机组出力的稳定性。

2.2 光伏出力场景构建
受天气变化、预测方法等因素影响,光伏预测出力与实际出力之间的偏差客观存在。文中以历史偏差数据为样本,采用模糊聚类分析,构建光伏出力场景,具体方法流程如下。
1)出力偏差处理
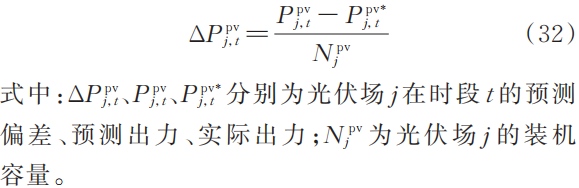
2)模糊聚类分析
以光伏场站历史日内96 点预测出力与实际出力偏差曲线为样本,进行模糊聚类分析,并采用聚类综合质量确定最佳聚类数,最后以各类别的模糊聚类中心构建预测出力偏差场景,具体公式和详细步骤可参考文献[29]。
3)光伏出力场景

2.3 求解流程
本文所述的互补系统最大化可消纳电量期望模型的求解步骤如下:
步骤 1:读取基础数据并设置计算条件。包括区间流量、梯级发电计划、光伏预测出力、光伏历史预测与实际出力、分区断面约束、爬坡能力等。
步骤 2:模型转换处理。采用 2.1 节所述模型转换方法,对非线性约束进行线性化处理。
步骤 3:光伏出力场景构建。根据计划日光伏预测出力以及 2.2 节所述方法构建光伏出力场景。
步骤 4:模型求解。将目标函数与转化后的约束结合构成的 MILP 模型,在 Java 环境中,编码调用CPLEX 求解类,实现模型求解,附录 Á 给出了编码和求解示例。
步骤 5:结果输出。输出互补系统整体可消纳电量期望值,不同组合场景下的电站出力、机组出力、机组开停机、出库流量、水库水位等结果信息。
3.编程思路分析
3.1参数和变量定义
表1 相关参数
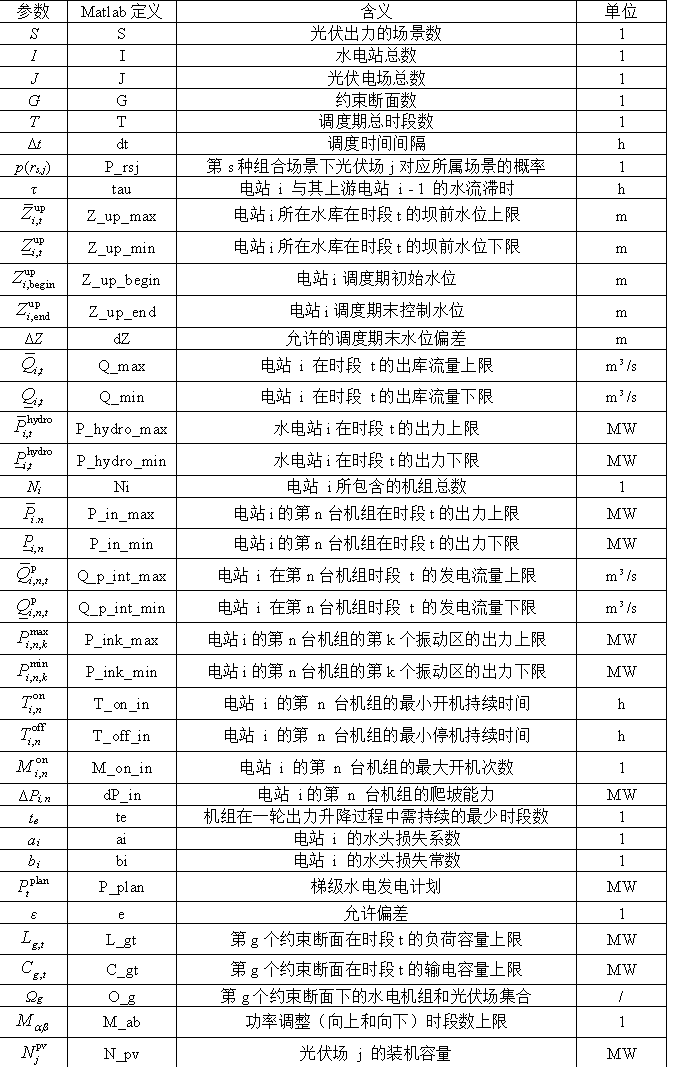
表2 决策变量
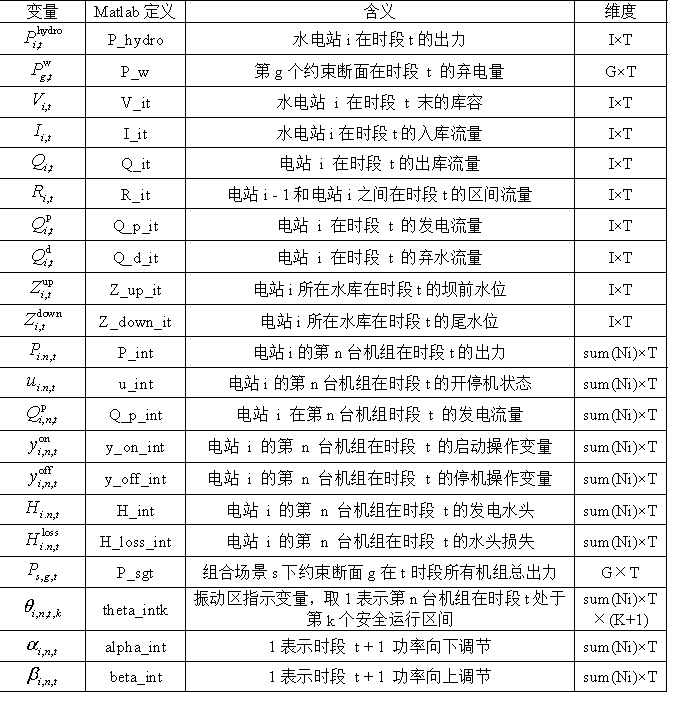
3.2编程思路
根据对文献内容的解读,可以设计下面的编程思路:
步骤1:输入所需数据
算例分析用到的部分数据可以从原文中找到,大部分数据文献中都没有给出,只能参考其他文献进行设置。然后将所有需要的数据,按照表1的定义格式输入即可。包括区间流量、梯级发电计划、光伏预测出力、光伏历史预测与实际出力、分区断面约束、爬坡能力等。
步骤2:光伏出力的场景生成与削减
这部分就是根据计划日光伏预测出力以及原文中2.2节所述方法构建光伏的出力场景。原文中只是简单提到采用了参考文献[29]中所用方法进行场景生成与削减,并未详细介绍,此类方法比较简单,网上也能找到很多示例。另外,本来这个模型就是涉及非常多0-1变量,问题规模比较大,如果再加上多个场景,变量的数目将呈倍数增加,所以在复现的代码中,我就没有写场景生成与缩减的程序,直接给出了数据,选取典型的光伏出力场景作为算例。如果有需要的话可以自己修改数据,或者加入场景生成与削减的代码。
步骤3:定义决策变量
这一步比较简单,按照表2,初始化决策变量即可,同时每个决策变量的维度以及类型(sdpvar还是binvar)不要出错。另外,代码中变量定义的方式和文献中稍微有点不一样,这里不再详细介绍,具体可以去代码中查看。
步骤4:写目标函数和约束条件
写目标函数比较简单,按照给定的数据和定义的变量,写出目标函数即可。约束条件的处理比较复杂,文中只给出了约束条件16和19的线性化方法,其他几个非线性约束都是一笔带过,只说了用到某某文献中的方法。方便起见,我在这里把所有非线性约束都写出来,并介绍处理方法:
1)式10
原文中只给出了水位和库容的关系示意,一般情况下水位可以表示为库容的三次多项式,具体如下:

四个不同的水电站水位-库容关系可以分别表示为:
y1=0.0006x^3-0.0811x^2+4.769x+1031, 10<=x<=45
y1=0.0269x^3-0.8958x^2+14.77x+891.8, 3.6<=x<=8.8
y1=0.01307x^3-0.699x^2+10.41x+803.5, 10<=x<=25
y1=0.005465x^3-0.1435x^2+3.495x+700.2, 5<=x<=22
针对上述非线性函数关系,可采用分段线性化的方法将其转为线性约束,如图所示:
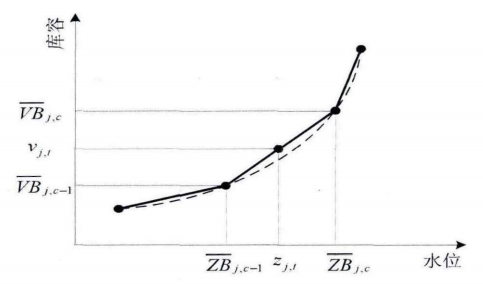
2)式11
尾水位是泄流量的非线性函数,通常表示为泄流量的2次多项式:

四个不同的水电站尾水位-泄流量关系可以分别表示为:
y2=7.619e-07q^2-0.000672q+976.1
y2=7.081e-08q^2-9.372e-05q+839.1
y2=7.086e-08q^2+0.00032345q+752.6
y2=1.327e-07q^2-0.0005827q+655.9
针对上述非线性函数关系,可采用分段线性化的方法将其转为线性约束,和约束10处理方法一致。
3)式16、19
原文中有详细解释,此处不再赘述。
4)式21
约束21是一个二次约束,也可以通过分段线性化的方式转为线性约束。不再赘述。
5)式22
水电站的非线性出力曲线,可以表示如下:
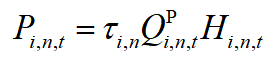
为了说明采用三角权值法是如何对这个表达式进行线性化的,首先把表达式简化如下:
![]()
假设将Q的取值范围分为n1-1个区间,区间的端点值分别为Q1,Q2,...,Qn1,将H的取值范围分为n2-1个区间,区间的端点值分别为H1,H2,...,Hn2。那么对于任意的Q和H,都可以表示为区间端点值的线性组合,例如Q的取值在Q1和Q2之间,就可以用Q1和Q2表示Q,H的取值范围在H3和H4之间,就可以用H3和H4表示H。
我们令pij=Hi×Qj,那么表达式也可以表示为:
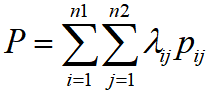
下面举个例子,假设H取值范围是[10,25],分为3个区间,区间端点分别为H1=10, H2=15, H3=20, H4=25,H取值范围是[80,100],分为4个区间,区间端点分别为H1=80, H2=85,H3=90, H4=95, H5=100。假设H是13,Q是86,就可以写成H=0.6H1+0.4H2,Q=0.8Q2+0.2Q3,QH就可以写成(0.6H1+0.4H2)(0.8Q2+0.2Q3)。也就是λ21=0.6×0.8,λ31=0.6×0.2,λ22=0.4×0.8,λ32=0.4×0.2。因此,可以将机组的输出功率表示为变量λij和已知量pij的表达式,从非线性表达式转为线性表达式。
步骤5:求解模型
原文中使用的是java和cplex求解,这份代码使用的是matlab+yalmip+cplex求解。
步骤6:输出结果
按原文中的格式输出优化结果,但由于文中提供的数据非常少,大部分数据都是自己设定的,所以结果肯定不一样,但原理都是一样的。
4.Matlab代码
完整的matlab代码可以从这个链接获取:
https://download.csdn.net/download/weixin_44209907/88130711
5.运行结果分析
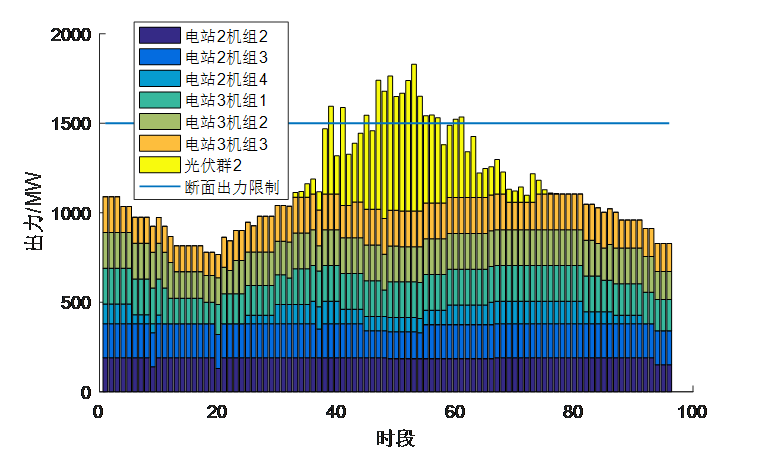
5.1光伏出力曲线
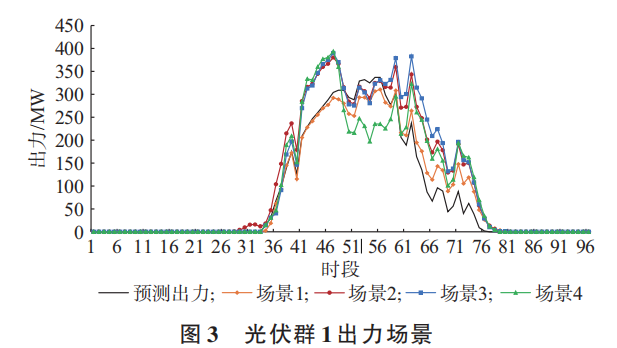

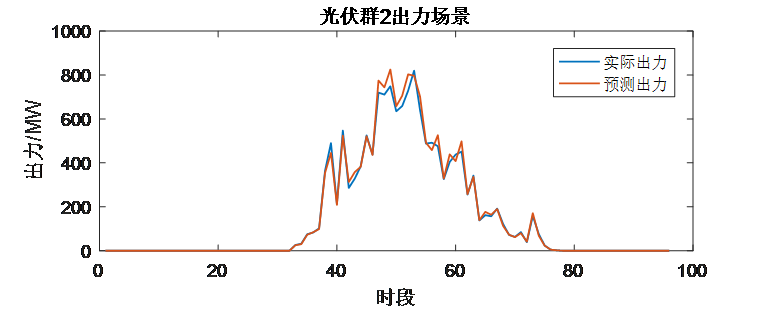 5.2运行机组台数
5.2运行机组台数
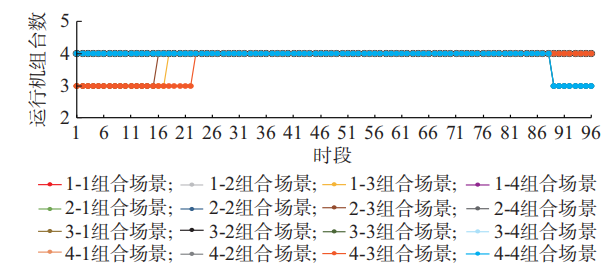
 5.3梯级水电站群出力
5.3梯级水电站群出力
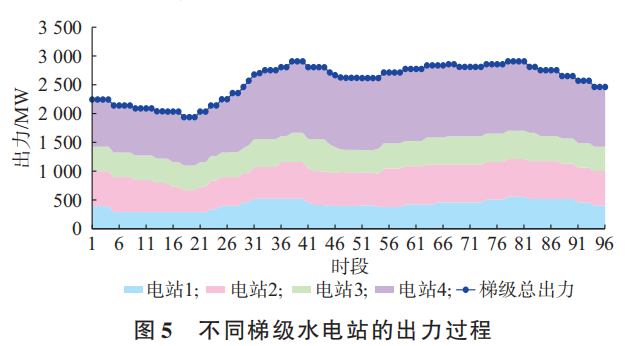

5.4水电机组出力
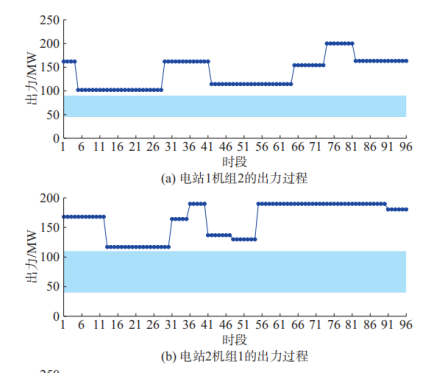
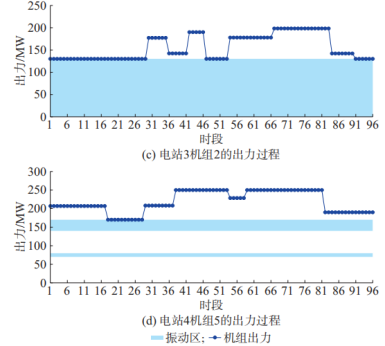
 5.5梯级水电站水位变化
5.5梯级水电站水位变化
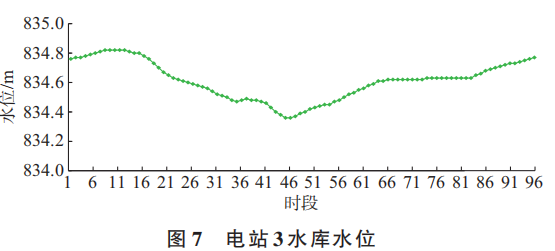
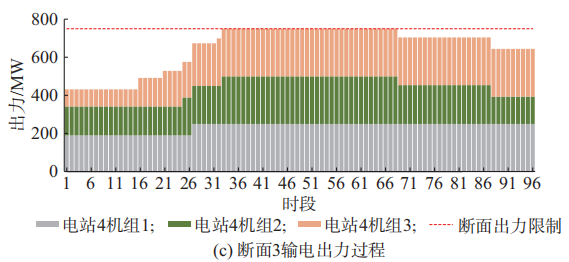
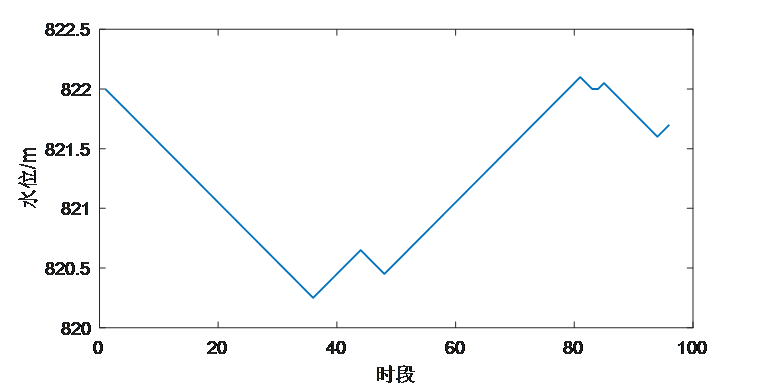 5.6各个断面出力
5.6各个断面出力

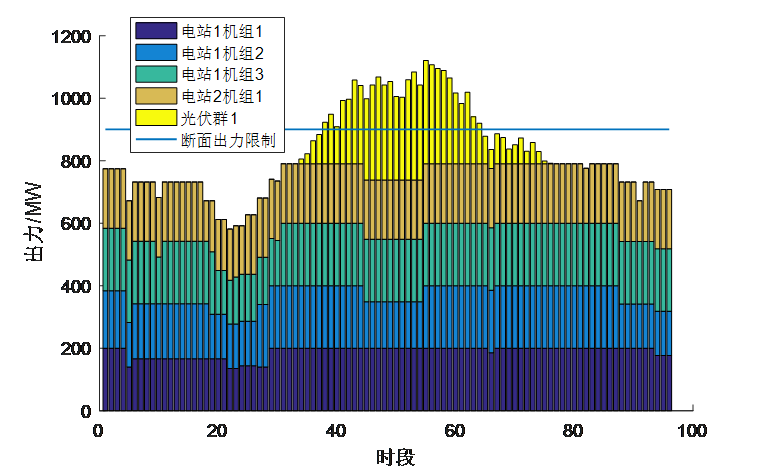
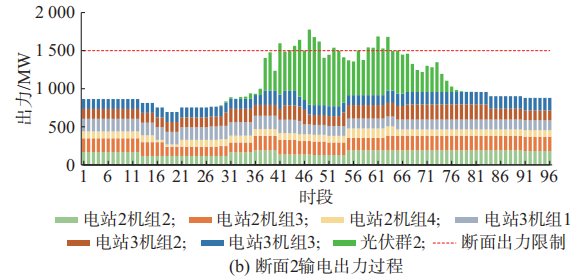

相关文章:

(文章复现)梯级水光互补系统最大化可消纳电量期望短期优化调度模型matlab代码
参考文献: [1]罗彬,陈永灿,刘昭伟等.梯级水光互补系统最大化可消纳电量期望短期优化调度模型[J].电力系统自动化,2023,47(10):66-75. 1.基本原理 1.1 目标函数 考虑光伏出力的不确定性,以梯级水光互补系统的可消纳电量期望最大为目标,函数…...

tinkerCAD案例:24. Ruler - Measuring Lengths 标尺 -量勺
tinkerCAD案例:24. Ruler - Measuring Lengths 标尺 - 测量长度 Project Overview: 项目概况: A machine shop, where any idea can become a reality, can cost millions and million of dollars. Still, the most important tool in the shop is the…...

linux系统编程重点复习--线程同步
目录 复习目标: 1 互斥锁 1.1互斥锁的使用步骤 1.2 练习 1.3 死锁 2 读写锁 3 条件变量 4 信号量 复习目标: 熟练掌握互斥量的使用说出什么叫死锁以及解决方案熟练掌握读写锁的使用熟练掌握条件变量的使用理解条件变量实现的生产消费者模型理解…...
【Docker 学习笔记】Windows Docker Desktop 安装
文章目录 一、前言二、Windows Docker 安装1. 基于Hyper-V后端和Windows容器的安装2. 基于WSL2后端的安装(推荐)3. 安装Docker Desktop on Windows4. 启动并验证Docker Desktop 一、前言 Docker并非是一个通用的容器工具,它依赖于已存在并运…...

getInputStream has already been called for this request 问题记录
问题背景 HttpServletRequest.getReader() HttpServletRequest.getInputStream() 不能在过滤器中读取一次二进制流(字符流),又在另外一个Servlet中读取一次,即一个InputSteam(BufferedReader)对象在被读取完成后,将无…...
)
日撸代码300行:第60天(小结)
1、自己对于这个专栏的代码抄写也是断断续续,由于种种原因上次在第54天没坚持下来,这次继续希望能抄完。 2、现在代码的阅读和理解能力明显比刚开始抄代码的时候强了不少。感觉坚持到现在收获还是不小。现在基本上来说仔细想一下都能够理清楚代码的意思。…...

python和java哪个更有前景,python和java哪个更有前途
大家好,小编为大家解答python和java哪个好学,零基础的问题。很多人还不知道python和java哪个更容易入门,现在让我们一起来看看吧! 进入编程行业是很多人的梦想,现在越来越多的人都想要通过培训的方式进入IT行业中,但是…...
LeetCode_11. 盛最多水的容器
题目描述 11. 盛最多水的容器 - 力扣(LeetCode)https://leetcode.cn/problems/container-with-most-water/ 思路分析 这题就是典型的是一道很经典的面试题,最优的解法是双指针,但很多人在第一次看到这题的时候很难想到用双指针来…...

【Android】APP电量优化学习笔记
电量优化原因 电量优化在 Android 开发中非常重要,原因如下: 用户体验: 电池续航时间是用户在使用移动设备时非常关注的因素之一。通过进行电量优化,可以延长设备的电池寿命,使用户能够更长时间地使用设备而不必频繁…...
【微信小程序创作之路】- 小程序事件绑定、动态提示Toast、对话框 Modal
【微信小程序创作之路】- 小程序事件绑定、动态提示Toast、对话框 Modal 第六章 小程序事件绑定、动态提示Toast、对话框 Modal 文章目录 【微信小程序创作之路】- 小程序事件绑定、动态提示Toast、对话框 Modal前言一、事件是什么?二、小程序中常用事件三、事件传…...
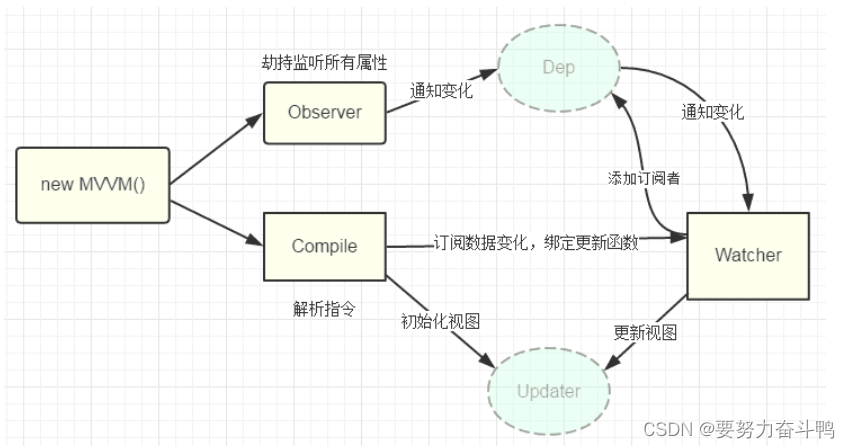
MVC与MVVM模式的区别
一、MVC Model(模型):用于处理应用程序数据逻辑,负责在数据库中存取数据。处理数据的crud View(视图):处理数据显示的部分。通常视图是依据模型数据创建的。 Controller(控制器&…...
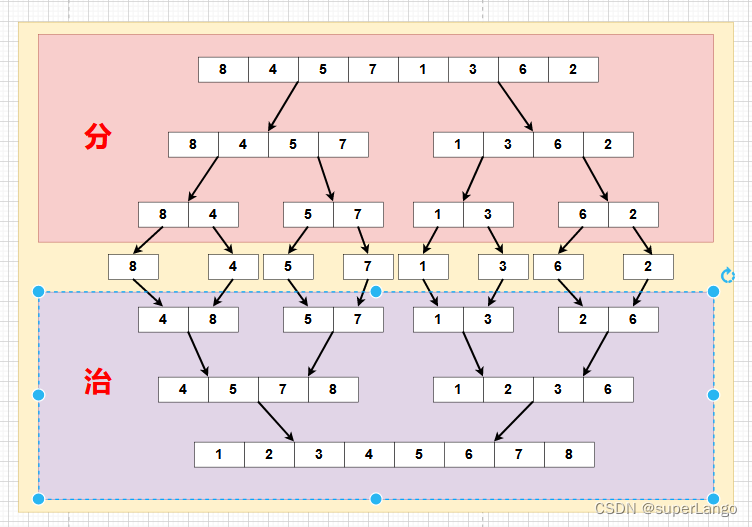
【数据结构与算法】归并排序
归并排序 归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而…...

OSG3.6.5 + VS2017前期准备及编译
OSG3.6.5 VS2017前期准备及编译 1、前期准备 1.1、osg稳定版本源码 Stable releases (openscenegraph.com) 1.2、osg依赖项 Dependencies (openscenegraph.com) 1.3、osg测试及演示数据 Data Resources (openscenegraph.com) 1.4、安装doxygen和Graphviz(用…...
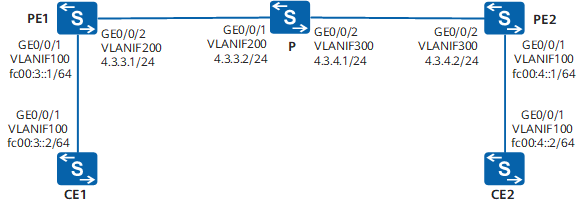
IPv6 over IPv4隧道配置举例
配置IPv6 over IPv4手动隧道示例 组网需求 如图1所示,两台IPv6主机分别通过SwitchA和SwitchC与IPv4骨干网络连接,客户希望两台IPv6主机能通过IPv4骨干网互通。 图1 配置IPv6 over IPv4手动隧道组网图 配置思路 配置IPv6 over IPv4手动隧道的思路如下&…...
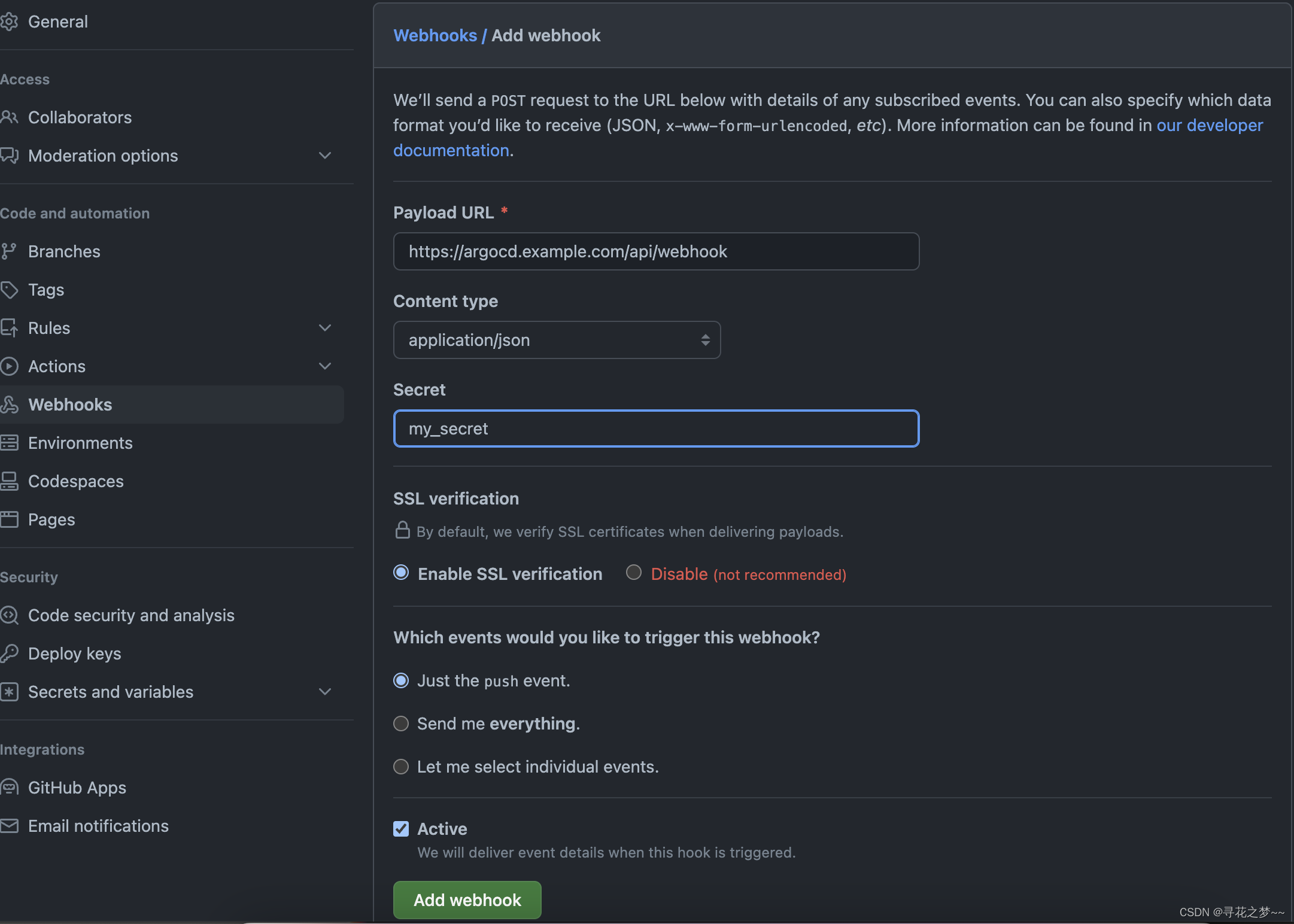
【GitOps系列】使用 ArgoCD 快速打造GitOps工作流
文章目录 ArgoCD简介ArgoCD安装访问ArgoCDGitOps 工作流总览创建 ArgoCD 应用检查 ArgoCD 同步状态访问应用 连接 GitOps 工作流体验 GitOps 工作流生产建议1)修改默认密码2)配置 Ingress 和 TLS3)使用 Webhook 触发 ArgoCD4)将源…...
C#|无法打开cs文件设计窗口
报错信息:To prevent possible data loss before loading the designer, the following errors must be resolved: 解决方案:实不相瞒我把项目解决方案名称改短了就可以了。。有其他原因或者解决方案望不吝赐教。。...

【SpringBoot笔记36】SpringBoot自定义WebSocketHandler集成WebSocket
这篇文章,主要介绍SpringBoot自定义WebSocketHandler集成WebSocket。 目录 一、SpringBoot集成WebSocket 1.1、添加WebSocket依赖 1.2、自定义WebSocketHandler 1.3、注册WebSocket服务端...

flutter 图片相关
官方链接:https://api.flutter.dev/flutter/widgets/Image-class.html 图片基本使用 显示本地图片时,要在pubspec.yaml文件里面添加如:(注意空格) assets: - assets/images/logo.png Fit属性: BoxFit.cover最常用 显示可能拉伸,可能裁…...

将上位机程序从PC的window系统迁移至Intel NUC的无桌面版ubuntu系统问题记录
将上位机程序从PC的window系统迁移至Intel NUC的无桌面版ubuntu系统 问题一 网口失效 问题描述:NUC关机状态下,将网口与路由器连接,网络指示灯闪烁;NUC开机后,网络指示灯熄灭,使用ping命令,既…...
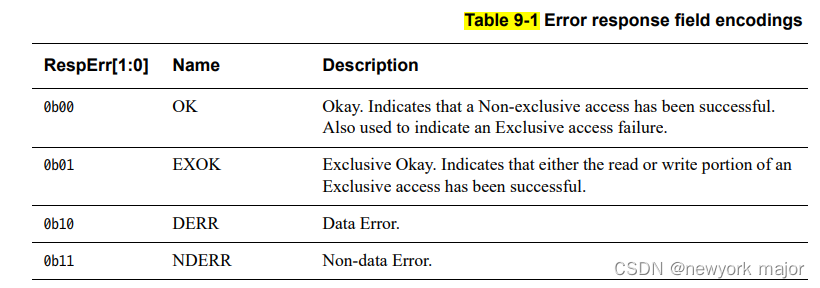
CHI中的error处理
Error Handling Error types 包含两种sub-packet级别的error, 和两种packe级别的error; Packet level error Data Error, DERR □ 访问的地址是正确的,但是访问的数据有错误;通常是在数据崩溃的时候使用,例如ECC…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...
