【C++】 哈希
一、哈希的概念及其性质
1.哈希概念
在顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找一个元素时,必须要经过关键码的多次比较。比如顺序表需要从第一个元素依次向后进行查找,顺序查找时间复杂度为O(N),平衡树中需要从第一层开始逐层往下进行比较,查找的次数为树的高度,即O(logN),搜索的效率取决于搜索过程中元素的比较次数
尽管红黑树或者AVL树的查找效率已经很高了,但是还是不够极致,理想的搜索方法:可以不经过任何比较,一次直接从表中得到要搜索的元素。
如果构造一种存储结构,通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时通过该函数可以很快找到该元素,当向该结构中:
插入元素时 : 根据待插入元素的关键码,以此函数计算出该元素的存储位置并按此位置进行存放
搜索元素时 : 对元素的关键码进行同样的计算,把求得的函数值当做元素的存储位置,在结构中按此位置取元素比较,若关键码相等,则搜索成功
该方式即为哈希(散列)方法,哈希方法中使用的转换函数称为哈希(散列)函数,构造出来的结构称为哈希表(Hash Table)(或者称散列表)
我们需要注意的是,不管是顺序查找,平衡树查找还是哈希查找,其key值都是唯一的,也就是说,搜索树和哈希表中都不允许出现相同的key 值
2.哈希函数
哈希函数设计原则:
1.哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m个地址时,其值域必须在0到m-1之间
2.哈希函数计算出来的地址能均匀分布在整个空间中
3.哈希函数应该比较简单
常见哈希函数
1.直接定址法–(常用)
直接定址法取关键字的某个线性函数为散列地址:Hash(Ke)= A*Key + B
它的优点是简单,且不会引起哈希冲突–哈希冲突是指多个不同的key值映射到同一个存储位置,由于直接定址法的key值经过哈希函数转换后得到的值一定是唯一的,所以不存在哈希冲突
直接定址法适用于数据范围比较集中的情况,这样key值映射到哈希表之后,哈希表的空间利用率高,浪费非空间较少,不适用与数据分散的情况,因为这样会导致空间的利用率很低,从而造成空间浪费
下面是一道哈希定址法的典型例子:
387.字符串中第一个唯一字符[LeetCode]
class Solution {
public:int firstUniqChar(string s) {int arr[26]={0};for(size_t i=0;i<s.size();++i){// 题目中说明只有小写字母,我们减去字符得到的数作为下标arr[s[i]-'a']++;}// 遍历查找第一个为1的下标for(size_t i=0;i<s.size();++i){if(arr[s[i]-'a']==1){return i;}}return -1;}
};
2.除留余数法–(常用)
除留余数法思想 : 设散列表中允许的地址数为m,取一个不大于m,但最接近或者等于m的质数p作为除数,按照哈希函数:Hash(key) = key% p(p<=m),将关键码转换成哈希地址
我们使用key值对哈希表的大小进行取模得到的树作为哈希映射的地址,将key保存到该地址中,除留余数法的优点是可以处理数据范围分散的数据,缺点是会引发哈希冲突,比如对于数据集合:
数据集合{1,7,6,4,5,9};
哈希函数设置为:hash(key) = key % capacity; capacity为存储元素底层空间总的大小。

此时,如果我们继续插入数据11,那么通过哈希函数计算出应该存储在下标为1的位置,但是下标为 1的位置引进存放了数据1,此时就会发生哈希冲突
3.平方取中法–(了解)
假设关键字为1234,对它平方就是1522756,抽取中间的3位227作为哈希地址;再比如关键字为4321,对它平方就是18671041,抽取中间的3位671(或710)作为哈希地址
平方取中法比较适合:不知道关键字的分布,而位数又不是很大的情况
4.折叠法–(了解)
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些),然后将这几部分叠加求和,并按散列表表长,取后几位作为散列地址。
折叠法适合事先不需要知道关键字的分布,适合关键字位数比较多的情况
5.随机数法–(了解)
选择一个随机函数,取关键字的随机函数值为它的哈希地址,即H(key) = random(key),其中random为随机数函数。
通常应用于关键字长度不等时采用此法
6.数学分析法–(了解)
设有n个d位数,每一位可能有r种不同的符号,这r种不同的符号在各位上出现的频率不一定相同,可能在某些位上分布比较均匀,每种符号出现的机会均等,在某些位上分布不均匀只有某几种符号经常出现。可根据散列表的大小,选择其中各种符号分布均匀的若干位作为散列地址。
假设要存储某家公司员工登记表,如果用手机号作为关键字,那么极有可能前7位都是 相同的,那么我们可以选择后面的四位作为散列地址,如果这样的抽取工作还容易出现 冲突,还可以对抽取出来的数字进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环移位、前两数与后两数叠加(如1234改成12+34=46)等方法

数字分析法通常适合处理关键字位数比较大的情况,如果事先知道关键字的分布且关键字的若干位分布较均匀的情况
注意:哈希函数设计的越精妙,产生哈希冲突的可能性就越低,但是无法避免哈希冲突
3.哈希冲突
对于两个数据元素的关键字字 k i k_i ki和 K_j(i != j),有 k i k_i ki != k j k_j kj,但有:Hash( k i k_i ki) == Hash( k j k_j kj),即:不同关键字通过相同哈希哈数计算出相同的哈希地址,该种现象称为哈希冲突或哈希碰撞
解决哈希冲突两种常见的方法是:闭散列和开散列
1.闭散列:也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那么可以把key存放到冲突位置中的“下一个”空位置中去
2.开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中,即发生哈希冲突之后,把key直接链接在该位置的下面
二、闭散列
闭散列:也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那么可以把key存放到冲突位置中的“下一个”空位置中去。那如何寻找下一个空位置呢?这里有两种方法–线性探测法和二次探测法
1.线性探测
线性探测法是指从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止,比如下面的场景中,现在需要插入元素44,先通过哈希函数计算哈希地址,hashAddr为4,因此44理论上应该插在该位置,但是该位置已经放了值为4的元素,即发生哈希冲突,则我们可以向后寻找一个空的位置即下标为8 的位置进插入

下面我们来模拟实现哈希函数的除留余数法,并使用闭散列的线性探测法来解决哈希冲突的问题
2.哈希表的基本框架
哈希表节点结构的定义如下:
#pragma once
#include <vector>namespace closeHash
{// 定义一个位置的状态enum state{EMPTY, // 空EXIST, // 存在数据DELETE, //该位置数据被删除};// 哈希表每个节点下标位置存储的数据的结果template<class K,class V>struct HashData{pair<K, V> _kv;state _state = EMPTY; // 默认为空};template<class K,class V, class Hash = HashFunc<K>>class HashTable{typedef HashData<K, V> Data;private:vector<Data> _tables;size_t _n = 0; // 表中存储的有效数据的个数};
}
为了方便,在哈希表中我们使用vector来存储数据,并增加了一个变量n来记录表中有效数据的个数,同时,哈希表的每一个下标位置存储的数据都是一个KV模型的键值对,此外我们还需要使用一个state变量来记录每一个位置的状态。
原因是因为我们可能是删除哈希表中的数据,但是我们在插入的时候,当key映射的下标位置被占用时,key会向后寻找下一个空的位置进行插入,但是如果key走到数据尾部还没有找到就会从数组的起始位置开始寻找。 假如我们删除了其中的一个节点,此时我们需要查找一个节点,由于被占用的原因该节点在被删除节点的位置的后面,我们一步一步向后找的时候,在走到被删除节点的位置,发现该位置没有数据之后就会返回false,但事实上这个数据是存在的,即使我们说删除之后我们将该位置的数据修改为一个数字,但是选择哪一个呢?0,-1/1都不合适,因为插入的数据是可能的任何数据,但是当我们使用一个state来标识一个位置的状态的时候,我们查找走到已经被删除位置的时候,发现该位置的数据被删除了,但是查找会继续向后进行查找。
所以,在哈希表中每个位置的数据增加了一个state变量类似标记该位置的状态。
3.哈希表的操作
1.哈希表的插入
插入一个分为两步:
1.通过哈希函数获取待插入元素在哈希表中的位置
2.如果该位置中没有元素则直接插入新元素,如果该位置中有元素发生哈希冲突,使用线性探测找到下一个空位置,插入新元素
我们插入的时候需要考虑扩容的问题,这个我们在哈希表扩容的时候再进行详细的讲解。
插入代码如下:
template<class K>
struct HashFunc
{size_t operator()(const K& key){return (size_t)key;}
};
// 插入
bool Insert(const pair<K, V>& kv)
{// 已经存在该值返回falseif (Find(kv.first))return false;// 大于标定负载因子,就需要扩容if (_n * 10 / _tables.size() > 7){// 使用一个新的哈希表,进行插入,然后进行交换两个哈希表的_tablesHashTable<K, V> newHT;newHT._tables.resize(_tables.size() * 2);for (auto& e : _tables){if (e._state == EXIST){newHT.Insert(e._kv);}}_tables.swap(newHT._tables);}Hash hf;size_t hashi = hf(kv.first) % _tables.size();while (_tables[hashi]._state == EXIST){hashi++;hashi %= _tables.size();}//插入之后将该位置的状态该为存在_tables[hashi]._kv = kv;_tables[hashi]._state = EXIST;++_n;return true;
}
2.哈希表的查找
通过哈希函数得到余数即数组下标,取出下标位置的key与目标key进行比较,相等就返回该位置的地址,如果查找到状态为空的下标位置就返回nullptr,但是这样有几个需要注意的地方:
1.当遇到状态为空的下标位置才返回nullptr,而不是遇到状态为删除的位置就返回nullptr,因为我们要查找的数据可能在删除数据的后面
2.将查找函数的返回值定义为Data*,而不是bool,这样可以方便我们进行删除和修改(修改key对应的value),查找到之后直接通过指针的解引用修改value与state
3.哈希表经过不断的插入和删除,最终可能会出现一种极端的情况–哈希表中元素的状态全为EXIST和DELETE,此时如果我们找空就会造成死循环,所以我们需要对这种情况进行单独的处理
// 查找
// 查找返回那个位置的地址
Data* Find(const K& key)
{Hash hf;// 仿函数对象size_t hashi = hf(key) % _tables.size();// 记录hashi的起始位置,避免哈希表中元素全为EXISR和DELETE造成死循环size_t starti = hashi;while (_tables[hashi]._state != EMPTY){// key相等且state为EXIST才表示找到if (_tables[hashi]._state == EXIST && _tables[hashi]._kv.first == key){return &_tables[hashi];}++hashi;hashi %= _tables.size();// 如果找了一圈都没有找到,则跳出循环if(starti == hashi)break;}return nullptr;
}
3.哈希表的删除
哈希表的删除我们复用查找函数,查到到就通过查找函数的返回值将下标位置数据的状态置为DELETE即可,没有找到就返回false
代码如下:
// 删除
bool Erase(const K& key)
{Data* ret = Find(key);if (ret){// 删除之后将该位置的状态改为删除ret->_state = DELETE;--_n;return true;}else{return false;}
}
4.哈希表的扩容
哈希表的扩容和普通顺序表容器的扩容不同,它不是容器满了才进行扩容,而是会有一个负载因子,当负载因子 超过一定大小时才会进行扩容,书上对负载因子的表述如下:

哈希的扩容并不是简单的扩大空间,而是需要将已经插入到哈希表中的元素取出全部重新进行插入,因为扩容后会导致哈希表的长度改变,那么key通过哈希函数映射到的位置也会发生改变,所以需要重新进行插入
我们这里使用一个HashTable对象进行插入,然后交换二者的数组
// 插入
bool Insert(const pair<K, V>& kv)
{// 已经存在该值返回falseif (Find(kv.first))return false;// 大于标定负载因子,就需要扩容if (_n * 10 / _tables.size() > 7){// 使用一个新的哈希表,进行插入,然后进行交换两个哈希表的_tablesHashTable<K, V> newHT;newHT._tables.resize(_tables.size() * 2);for (auto& e : _tables){if (e._state == EXIST){newHT.Insert(e._kv);}}_tables.swap(newHT._tables);}Hash hf;size_t hashi = hf(kv.first) % _tables.size();while (_tables[hashi]._state == EXIST){hashi++;hashi %= _tables.size();}//插入之后将该位置的状态该为存在_tables[hashi]._kv = kv;_tables[hashi]._state = EXIST;++_n;return true;
}
5.哈希表的仿函数
我们插入的key值不是整数的时候,但是我们要让key与哈希表的长度取模得到映射位置,此时我们就需要进行两次转换,先将其他类型的数据转换成整数,再将该整数作为key转换为下标,比如我们统计水果数量的时候,就需要先将字符串转换为整数作为key值,然后再进行映射。
由于key值可以是不同类型的数据,我们不能只考虑字符串,字符串我们可以选择使用[]的方式获得第一个字符,但是对于其他类型就不再适用了,所以我们需要使用仿函数来帮我们解决这个问题。
我们可以为哈希表增加一个模板参数,给模板参数是一个仿函数,仿函数分为设计者提供的默认的仿函数和用户提供的仿函数,系统默认提供的仿函数可以将一些常见的key的类型全部转换为整形,比如字符串,指针,整数。而用户提供的仿函数则可以根据用户自己的需求将对应的key值转换为整形。
代码如下:
template<class K>
struct HashFunc
{size_t operator()(const K& key){return (size_t)key;}
};// 特化 --针对string类型写一个仿函数--转成整形
template<>
struct HashFunc<string>
{size_t operator()(const string& key){size_t hash = 0;for (auto& ch : key){hash *= 131;hash += ch;}return hash;}
};
有了仿函数之后,我们只需要在key与TableSize取模的地方使用仿函数对象将key转换为整形即可。这样,对于常见的key类型,哈希表可以通过内置的默认仿函数来完成下标的映射,对于用户自定义的key类型,需要我们自己提供对应的仿函数类来完成下标的映射
6.字符串的哈希算法
哈希表中key值的类型在我们日常生活中运用十分的广泛,我们可以取第一个字符来进行映射,但是这样很容易发生哈希冲突–只要字符串的首字母相同就会发生冲突,我们也可以考虑将字符串的所有字符的ASCII值加起来作为key值进行映射,但是对于这样的字符串–“abc" “acb” “bca” "aad"等等,这样的字符串的ASCII值相等也会发生哈希冲突
所有就有人专门研究看字符串哈希算法,即如何将字符串转换为整形可以使得将哈希冲突率变得很低,下面的一篇博客介绍了许多优秀非字符串哈希算法,我们可以借鉴学习学习:各种字符串Hash-clq-博客园(cnblogs.com)
其中BKDR哈希字符串算法是最出名也是平均分最高的,上面我们的代码中字符串算法就是使用的该算法
7.完整代码
这里我们需要注意的是,哈希表的拷贝构造,析构,赋值重载使用我们编译器默认生成的即可–对于自定义类型编译器会调用自定义类型的拷贝构造,析构和赋值重载,由于table是vector类型的成员变量,而vector中实现了深拷贝与析构,所以不需要我们自己来实现
HashTable.h
#pragma once#include <vector>template<class K>
struct HashFunc
{size_t operator()(const K& key){return (size_t)key;}
};// 特化 --针对string类型写一个仿函数--转成整形
template<>
struct HashFunc<string>
{size_t operator()(const string& key){size_t hash = 0;for (auto& ch : key){hash *= 131;hash += ch;}return hash;}
};namespace closeHash
{// 定义一个位置的状态enum state{EMPTY, // 空EXIST, // 存在数据DELETE, //该位置数据被删除};template<class K,class V>struct HashData{pair<K, V> _kv;state _state = EMPTY;};template<class K,class V, class Hash = HashFunc<K>>class HashTable{typedef HashData<K, V> Data;public:// 默认构造HashTable():_n(0){_tables.resize(10);}// 插入bool Insert(const pair<K, V>& kv){// 已经存在该值返回falseif (Find(kv.first))return false;// 大于标定负载因子,就需要扩容if (_n * 10 / _tables.size() > 7){// 使用一个新的哈希表,进行插入,然后进行交换两个哈希表的_tablesHashTable<K, V> newHT;newHT._tables.resize(_tables.size() * 2);for (auto& e : _tables){if (e._state == EXIST){newHT.Insert(e._kv);}}_tables.swap(newHT._tables);}Hash hf;size_t hashi = hf(kv.first) % _tables.size();while (_tables[hashi]._state == EXIST){hashi++;hashi %= _tables.size();}//插入之后将该位置的状态该为存在_tables[hashi]._kv = kv;_tables[hashi]._state = EXIST;++_n;return true;}// 查找
// 查找返回那个位置的地址Data* Find(const K& key){Hash hf;// 仿函数对象size_t hashi = hf(key) % _tables.size();// 记录hashi的起始位置,避免哈希表中元素全为EXISR和DELETE造成死循环size_t starti = hashi;while (_tables[hashi]._state != EMPTY){// key相等且state为EXIST才表示找到if (_tables[hashi]._state == EXIST && _tables[hashi]._kv.first == key){return &_tables[hashi];}++hashi;hashi %= _tables.size();// 如果找了一圈都没有找到,则跳出循环if (starti == hashi)break;}return nullptr;}// 删除bool Erase(const K& key){Data* ret = Find(key);if (ret){// 删除之后将该位置的状态改为删除ret->_state = DELETE;--_n;return true;}else{return false;}}private:vector<Data> _tables;size_t _n = 0; // 表中存储的有效数据的个数};
}
Test.cpp
#define _CRT_SECURE_NO_WARNINGS 1#include <iostream>
using namespace std;#include "HashTable.h"void TestHT1()
{closeHash::HashTable<int, int> ht;int a[] = { 18, 8, 7, 27, 57, 3, 38, 18 };for (auto e : a){ht.Insert(make_pair(e, e));}ht.Insert(make_pair(17, 17));ht.Insert(make_pair(5, 5));cout << ht.Find(7) << endl;cout << ht.Find(8) << endl;ht.Erase(7);cout << ht.Find(7) << endl;cout << ht.Find(8) << endl;
}void TestHT2()
{string arr[] = { "苹果", "西瓜", "香蕉", "草莓", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };//HashTable<string, int, HashFuncString> countHT;closeHash::HashTable<string, int> countHT;for (auto& e : arr){closeHash::HashData<string, int>* ret = countHT.Find(e);if (ret){ret->_kv.second++;}else{countHT.Insert(make_pair(e, 1));}}HashFunc<string> hf;cout << hf("abc") << endl;cout << hf("bac") << endl;cout << hf("cba") << endl;cout << hf("aad") << endl;
}
int main()
{//TestHT1();TestHT2();return 0;
}
8.二次探测
线性探测优点:实现非常简单,
线性探测缺点:一旦发生哈希冲突,所有的冲突连在一起,容易产生数据堆积”,即:不同关键码占据了可利用的空位置,使得寻找某关键码的位置需要许多次比较,导致搜索效率降低。如何缓解呢?
线性探测的缺陷是产生冲突的数据堆积在一块,这与其找下一个空位置有关系,因为找空位置的方式就是挨着往后逐个去找,因此二次探测为了避免该问题,找下一个空位置的方法为: H i H_i Hi = ( H 0 H_0 H0 + i 2 i^2 i2 )% m,或者: H i H_i Hi = ( H 0 H_0 H0 - i 2 i^2 i2 )% m。其中:i =1,2,3…, H 0 H_0 H0是通过散列函数Hash(x)对元素的关键码key进行计算得到的位置,m是表的大小。即根据余数找到下标位置,如果位置被占用,不是去挨着的下一个位置找,而是去余数+i的平方的位置找插入位置,其中i是寻找的次数
研究表明:当表的长度为质数且表装载因子a不超过0.5时,新的表项一定能够插入,而且任何一个位置都不会被探查两次。因此只要表中有一半的空位置,就不会存在表满的问题。在搜索时可以不考虑表装满的情况,但在插入时必须确保表的装载因子a不超过0.5,如果超出必须考虑增容
比散列最大的缺陷就是空间利用率比较低,这也是哈希的缺陷.最后二次探测法在一定程度上减轻了哈希冲突的概率,但也没有从根源上解决问题。
三、开散列
1.开散列概念
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中。
即在发生哈希冲突的时候,把key作为一个节点直接链接在对应下面位置的哈希桶

从上图可以看出,开散列中每个桶中放的都是发生哈希冲突的元素。
2.开散列的节点结构
由于开散列的不同冲突的元素之间不会相互影响,所以开散列不再需要status变量来记录每一个下面位置的状态,此外开散列的每个下标位置链接的都是一个哈希桶,所以vector中的每一个元素都是一个节点的指针,指向单链表中的第一个元素,所以_tables是一个指针数组,这样就不会去占用别人的位置,所以不管在插入还是查找方面,开散列都要比闭散列要更加的高效,所以C++STL中的unordered_set和unordered_map以及Java中的HashSet和HashMap的底层都是使用哈希表的开散列方式实现的。最后,为了使得不同类型的key都能够计算出其映射的下标位置,所以我们需要传递一个仿函数:
// 仿函数
template<class K>
struct HashFunc
{size_t operator()(const K& key){return (size_t)key;}
};// 特化 --针对string类型写一个仿函数--转成整形
template<>
struct HashFunc<string>
{size_t operator()(const string& key){size_t hash = 0;for (auto ch : key){hash *= 131;hash += ch;}return hash;}
};
// 哈希表达节点结构--单链表
template<class K, class V>
struct HashNode
{pair<K, V> _kv;HashNode<K, V>* _next;HashNode(const pair<K, V>& kv):_kv(kv), _next(nullptr){}
};// 哈希表
template<class K, class V, class Hash=HashFunc<K>>
class HashTable
{typedef HashNode<K, V> Node;
private:vector<Node*> _tables; //指针数组size_t _n;// 表中有效数据的个数
};
3.开散列的操作
1.开散列的插入
开散列插入和闭散列一样,首先需要根据key值与哈希表的大小得到映射的下标的位置,此外,由于哈希表中每个下标位置都是一个哈希桶,即一个单链表,那么我们插入的时候只需要将冲突的元素链接到哈希桶中即可。这里链接有两种方式:
1.将发生哈希冲突的元素链接到单链表的末尾,即尾插
2.将发生哈希冲突的元素链接到单链表的头部,即头插
但是由于单链表尾插需要从头结点开始遍历进行找尾,这样插入的效率就比较低,所以我们选择头插的方式
插入部分代码如下:
bool Insert(const pair<K, V>& kv)
{if (Find(kv.first))return false;//调用仿函数的匿名对象将key转换为整数size_t hashi = Hash()(kv.first) % _tables.size();// 头插Node* newnode = new Node(kv);newnode->_next = _tables[hashi];_tables[hashi] = newnode;++_n;return true;
}
2.开散列的查找
开散列的查找只需要根据取模得到下标,由于下标位置存储的是单链表首元素的地址,我们进行遍历即可
Node* Find(const K& key)
{size_t hashi = Hash()(key) % _tables.size();Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){return cur;}else{cur = cur->_next;}}return nullptr;
}
3.开散列的删除
和闭散列不同的是,开散列的删除不能直接通过查找函数的返回值进行删除,因为单链表在删除节点时还需要改变父节点的指向,让其指向下一个节点,和单链表的删除相同,所以我们需要遍历单链表找到删除的节点进行删除
bool Erase(const K& key)
{// 通过哈希映射站到下标位置size_t hashi = Hash()(key) % _tables.size();Node* prev = nullptr;Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){// 头删//if (prev == nullptr)if(cur == _tables[hashi]){//_tables[hashi] = nullptr;_tables[hashi] = cur->_next;}else{prev->_next = cur->_next;}delete cur;--_n;return true;}else{cur = cur->_next;prev = cur;}}return false;
}
4.开散列的扩容
桶的个数是一定的,随着元素的不断插入,每个桶中元素的个数不断增多,极端情况下,可能会导致一个桶中链表节点非常多,会影响的哈希表的性能,因此在一定条件下需要对哈希表进行增容,那该条件怎么确认呢?开散列最好的情况是:每个哈希桶中刚好挂一个节点,再继续插入元素时,每一次都会发生哈希冲突,因此,在元素个数刚好等于桶的个数时,可以给哈希表增容。
开散列最好的情况是每一个哈希桶中都只有一个元素,再继续插入元素的时候,每一次就会发生哈希冲突,因此,我们可以在元素的个数等于桶的个数的时候进行扩容,即负载因子为1
这样我们可以采用两种扩容的方式:
1.采用闭散列扩容的思路-通过复用insert函数来进行扩容,但是开散列每个插入的时候都需要新开辟节点,在插入完毕之后,我们还需要释放表中原来的节点,这样就会使得效率很低
2.我们可以创建一个vector,取出旧表中的每一个节点链接到新的表中,然后再交换旧表和新表,这样就没有开辟节点和释放节点的消耗了,从而大大提高了扩容的效率。注:我们不能直接将原表中的整个哈希桶链接到新表中,因为新表的大小改变后原表中的元素可能会映射到表的其他位置
所以开散列的析构函数需要我们自己实现,因为默认生成的析构函数不会释放掉哈希桶
我们每次扩容不一定都在扩容2倍,有人提出了表的大小为质数 的时候哈希冲突的概率会低一些,当使用质数作为除数时,能够更加均匀地散列key值,就会较少哈希冲突的发生。库中可以这样实现的,但是也不是必须的,所以我们这里使用一个数组,保存一组质数,大概是2倍的关系,但是在42亿之后就不会再进行扩容了,其实我们也不用担心,因为我们整数的数据一共才42亿,是可以存储得下的。
但是在某一些极端场景下,或者面对某些碰撞攻击时(对方知道我们好像表的长度以及取模的逻辑,这个时候就专门设计一些冲突的数据,使得效率就不变得很低),那么机会导致单链表的长度过长,从而降低哈希的查找与删除的效率。
为了应对这种情况,Java 8中使用的HashMap在使用红黑树来优化哈希冲突的情况,因为红黑树可以保证查找,插入和删除的时间复杂度为O(logN),效率就会比链表快很多,此外,C++11也引入了一个新的数据结构–开发定址哈希表(open addressing table),用于存储哈希冲突时的元素,开放定址哈希表是一种不使用链表来解决哈希冲突的实现方式。这种实现方式中,如果一个槽(slot)已经被占用了,就会尝试找到下一个可用的槽,直达找到一个空槽,因为开发地址哈希表可以更好的利用缓冲,从而提高查找性能。C++11之后的版本中,unordered_map的哈希桶使用了两种不同的数据结构,包括单链表和开放定址哈希表–当桶中元素较少时,使用链表,当桶的元素较多的时候,会自动转换为开放定址哈希表
STL源码中的实现:
// Note: assumes long is at least 32 bits.
static const int __stl_num_primes = 28;
static const unsigned long __stl_prime_list[__stl_num_primes] =
{53, 97, 193, 389, 769,1543, 3079, 6151, 12289, 24593,49157, 98317, 196613, 393241, 786433,1572869, 3145739, 6291469, 12582917, 25165843,50331653, 100663319, 201326611, 402653189, 805306457, 1610612741, 3221225473, 4294967291
};inline unsigned long __stl_next_prime(unsigned long n)
{const unsigned long* first = __stl_prime_list;const unsigned long* last = __stl_prime_list + __stl_num_primes;const unsigned long* pos = lower_bound(first, last, n);return pos == last ? *(last - 1) : *pos;
}扩容代码如下:
// 负载因子控制在1,超过就扩容
if (_tables.size() == _n)
{ 创建一个哈希表对象,然后进行插入,之后交换双方的vector//HashTable<K, V> newHT;//newHT._tables.resize(_tables.size() * 2);//for (size_t i = 0; i < _tables.size(); ++i)//{// Node* cur = _tables[i];// while (cur)// {// newHT.Insert(cur->_kv);// cur = cur->_next;// }//}//_tables.swap(newHT._tables);vector<Node*> newTables;//newTables.resize(_tables.size() * 2, nullptr);newTables.resize(__stl_next_prime(_tables.size()), nullptr);for (size_t i = 0; i < _tables.size(); ++i){Node* cur = _tables[i];while (cur){// 保存下一个节点Node* next = cur->_next;size_t hashi = Hash()(cur->_kv.first) % newTables.size();//进行头插cur->_next = newTables[i];newTables[i] = cur;cur = next;}_tables[i] = nullptr;}_tables.swap(newTables);
}
5.开散列完整代码实现
namespace buckethash
{template<class K, class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next;HashNode(const pair<K, V>& kv):_kv(kv), _next(nullptr){}};template<class K, class V, class Hash=HashFunc<K>>class HashTable{typedef HashNode<K, V> Node;public:// 构造HashTable():_n(0){_tables.resize(__stl_next_prime(0));}// 析构~HashTable(){for (size_t i = 0; i < _tables.size(); ++i){Node* cur = _tables[i];while (cur){Node* next = cur->_next;delete cur;cur = next;}_tables[i] = nullptr;}}bool Insert(const pair<K, V>& kv){if (Find(kv.first))return false;// 负载因子控制在1,超过就扩容if (_tables.size() == _n){ 创建一个哈希表对象,然后进行插入,之后交换双方的vector//HashTable<K, V> newHT;//newHT._tables.resize(_tables.size() * 2);//for (size_t i = 0; i < _tables.size(); ++i)//{// Node* cur = _tables[i];// while (cur)// {// newHT.Insert(cur->_kv);// cur = cur->_next;// }//}//_tables.swap(newHT._tables);vector<Node*> newTables;//newTables.resize(_tables.size() * 2, nullptr);newTables.resize(__stl_next_prime(_tables.size()), nullptr);for (size_t i = 0; i < _tables.size(); ++i){Node* cur = _tables[i];while (cur){// 保存下一个节点Node* next = cur->_next;size_t hashi = Hash()(cur->_kv.first) % newTables.size();//进行头插cur->_next = newTables[i];newTables[i] = cur;cur = next;}_tables[i] = nullptr;}_tables.swap(newTables);}size_t hashi = Hash()(kv.first) % _tables.size();// 头插Node* newnode = new Node(kv);newnode->_next = _tables[hashi];_tables[hashi] = newnode;++_n;return true;}Node* Find(const K& key){size_t hashi = Hash()(key) % _tables.size();Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){return cur;}else{cur = cur->_next;}}return nullptr;}bool Erase(const K& key){size_t hashi = Hash()(key) % _tables.size();Node* prev = nullptr;Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){// 头删//if (prev == nullptr)if(cur == _tables[hashi]){//_tables[hashi] = nullptr;_tables[hashi] = cur->_next;}else{prev->_next = cur->_next;}delete cur;--_n;return true;}else{cur = cur->_next;prev = cur;}}return false;}inline unsigned long __stl_next_prime(unsigned long n){static const int __stl_num_primes = 28;static const unsigned long __stl_prime_list[__stl_num_primes] ={53, 97, 193, 389, 769,1543, 3079, 6151, 12289, 24593,49157, 98317, 196613, 393241, 786433,1572869, 3145739, 6291469, 12582917, 25165843,50331653, 100663319, 201326611, 402653189, 805306457,1610612741, 3221225473, 4294967291};for (int i = 0; i < __stl_num_primes; ++i){if (__stl_prime_list[i] > _n){return __stl_prime_list[i];}}return __stl_prime_list[__stl_num_primes - 1];}private:vector<Node*> _tables;size_t _n;};
}
6.开散列与闭散列比较
应用链地址法处理溢出,需要增设链接指针,似乎增加了存储开销。事实上:由于开地址法必须保持大量的空闲空间以确保搜索效率,如二次探查法要求装载因子a <=0.7,而表项所占空间又比指针大的多,所以使用链地址法反而比开地址法节省存储空间。
相关文章:

【C++】 哈希
一、哈希的概念及其性质 1.哈希概念 在顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找一个元素时,必须要经过关键码的多次比较。比如顺序表需要从第一个元素依次向后进行查找,顺序查找时间复杂度为…...
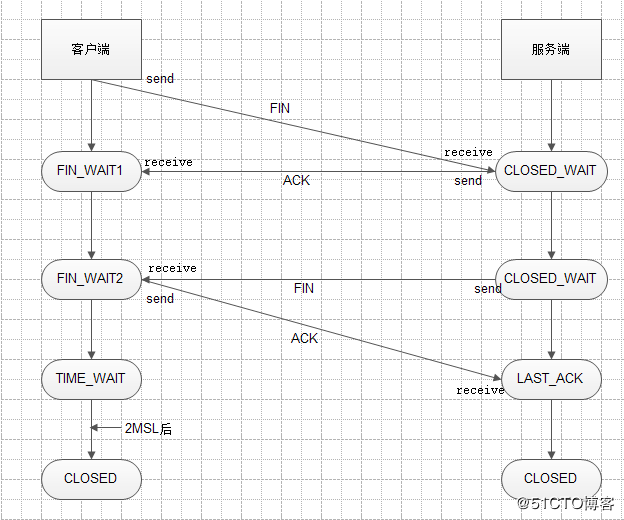
TCP三次握手和四次挥手以及11种状态(二)
11种状态 1、一开始,建立连接之前服务器和客户端的状态都为CLOSED; 2、服务器创建socket后开始监听,变为LISTEN状态; 3、客户端请求建立连接,向服务器发送SYN报文,客户端的状态变味SYN_SENT; 4、…...

【华为OD】运维日志排序
题目描述: 运维工程师采集到某产品线网运行一天产生的日志n条,现需根据日志时间先后顺序对日志进行排序,日志时间格式为H:M:S.N。 H表示小时(0~23) M表示分钟(0~59) S表示秒(0~59) N表示毫秒(0~999) 时间可能并没有补全,也就是说&…...
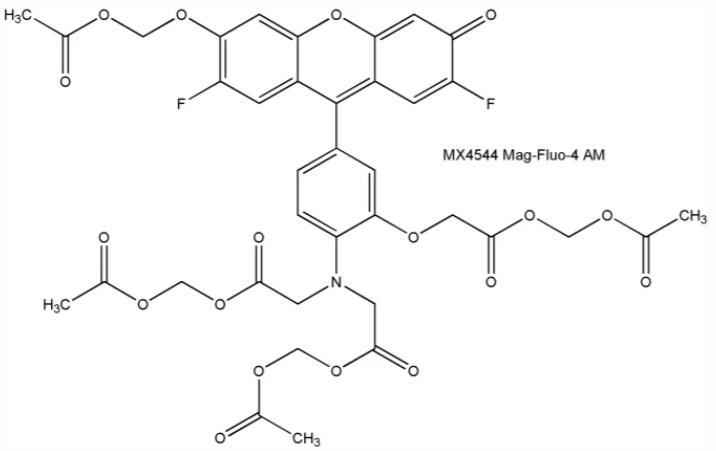
Mag-Fluo-4 AM,镁离子荧光探针,是一种有用的细胞内镁离子指示剂
资料编辑|陕西新研博美生物科技有限公司小编MISSwu PART1----产品描述: 镁离子荧光探针Mag-Fluo-4 AM,具细胞膜渗透性,对镁离子(Mg2) 和钙离子(Ca2)的 Kd 值分别是 4.7mM 和 22mM,…...

与 ChatGPT 进行有效交互的几种策略
在这篇文章中,您将了解即时工程。尤其, 如何在提示中提供对响应影响最大的信息什么是角色、正面和负面提示、零样本提示等如何迭代使用提示来利用 ChatGPT 的对话性质 废话不多说直接开始吧!!! 提示原则 快速工程是有…...
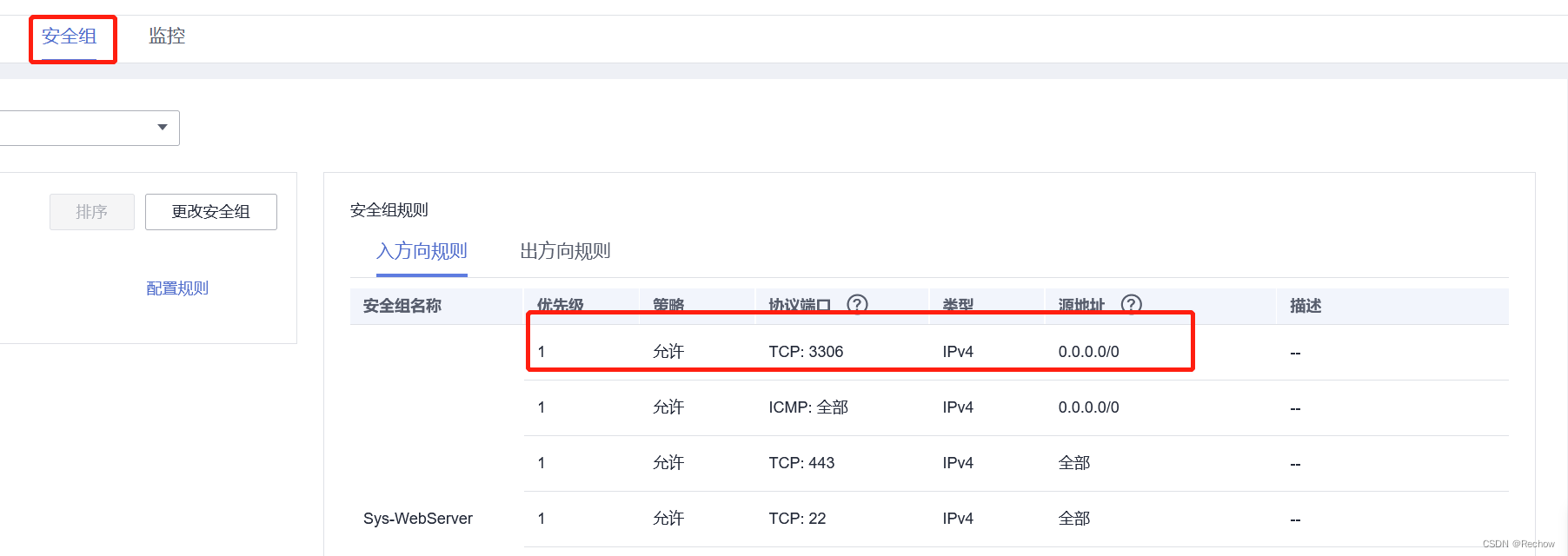
华为云安装MySQL后,本地工具连接MySQL失败
华为云安装MySQL后,本地连接失败 排查问题步骤: 在此之前需要在MySQL创建用户,并赋予权限。 1、能否ping通。 在本地命令行(Windows:winR)通过ping命令,ping服务器地址,看能否ping通。不能则需要检查本地…...

Flink On Yarn模式部署与验证
session运行模式 该模式下分为2步,即使用yarn-session.sh申请资源,然后 flink run提交任务。 1、申请资源yarn-session.sh #在server1执行命令 /usr/local/flink-1.13.5/bin/yarn-session.sh -tm 1024 -n 2 -s 1 -d #申请2个CPU、2g内存 # -tm 表示每个…...
[数据库]对数据库事务进行总结
文章目录 1、什么是事务2、事务的特性(ACID)3、并发事务带来的问题4、四个隔离级别: 1、什么是事务 事务是逻辑上的一组操作,要么都执行,要么都不执行。 事务最经典也经常被拿出来说例子就是转账了。假如小明要给小红…...

【Lua学习笔记】Lua进阶——Table(2)
文章目录 Table的一万种用法二维数组类和结构体Table操作insert & removesortconcat 接上文【Lua学习笔记】Lua进阶——Table,迭代器 Table的一万种用法 二维数组 a {{ 1, 2, 3 },{ 4, 5, 6 }, } print(#a) -->2 for i1,#a dob a[i]for j1,#b doprint(b[…...

如何进行软件回归测试
什么是软件回归测试,如何进行回归测试,进行回归测试时有哪些常用的方法? 回归测试是指修改了旧代码后,重新进行测试以确认修改没有引入新的错误或导致其他代码产生错误的一种测试方法。回归测试是指重复以前的全部或部分的相同功能…...
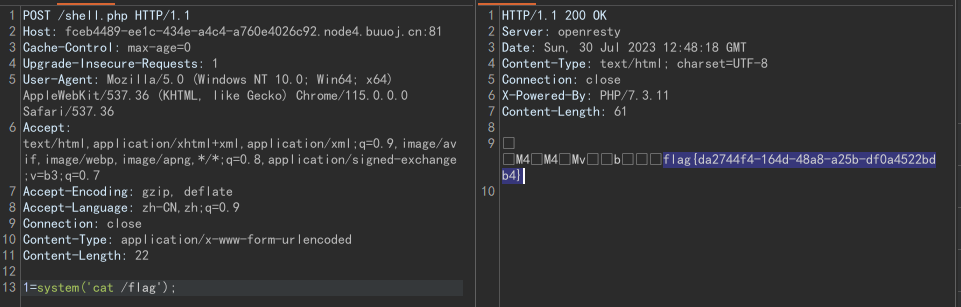
php://filter绕过死亡exit
文章目录 php://filter绕过死亡exit前言[EIS 2019]EzPOP绕过exit 参考 php://filter绕过死亡exit 前言 最近写了一道反序列化的题,其中有一个需要通过php://filter去绕过死亡exit()的小trick,这里通过一道题目来讲解 [EIS 2019]EzPOP 题目源码&#…...
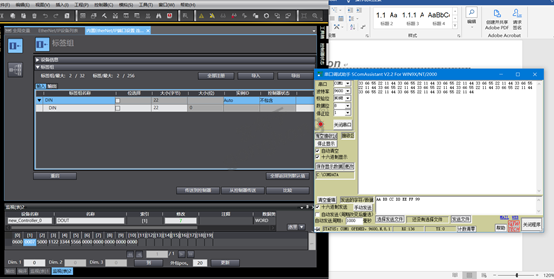
RS485/RS232自由转ETHERNET/IP网关profinet和ethernet区别
你是否曾经遇到过这样的问题:如何将ETHERNET/IP网络和RS485/RS232总线连接起来呢?捷米的JM-EIP-RS485/232通讯网关,自主研发的ETHERNET/IP从站功能,完美解决了这个难题。这款网关不仅可以将ETHERNET/IP网络和RS485/RS232总线连接起…...
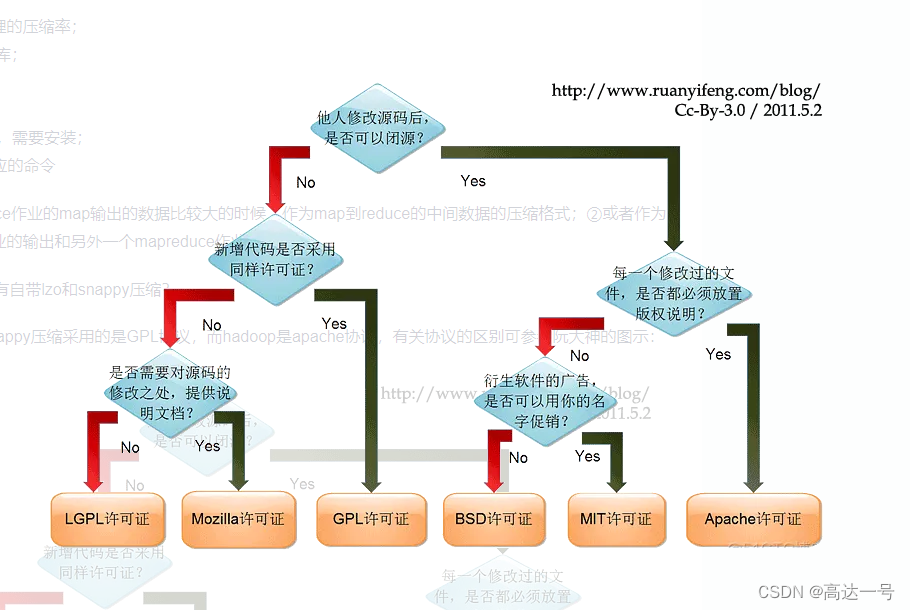
Hadoop_HDFS_常见的文件组织格式与压缩格式
参考资料 1. HDFS中的常用压缩算法及区别_大数据_王知无_InfoQ写作社区 2. orc格式和parquet格式对比-阿里云开发者社区 3.Hadoop 压缩格式 gzip/snappy/lzo/bzip2 比较与总结 | 海牛部落 高品质的 大数据技术社区 4. Hive中的文件存储格式TEXTFILE、SEQUENCEFILE、RCFILE…...
算法与数据结构(四)--排序算法
一.冒泡排序 原理图: 实现代码: /* 冒泡排序或者是沉底排序 *//* int arr[]: 排序目标数组,这里元素类型以整型为例; int len: 元素个数 */ void bubbleSort (elemType arr[], int len) {//为什么外循环小于len-1次?//考虑临界情况…...

【C/C++】C++11 在各编译器版本支持详情
C11 是在 2011 年发布的 C 标准,各编译器对 C11 的支持情况如下: GCC:GCC 4.8 及以上版本支持 C11。Clang:Clang 3.3 及以上版本支持 C11。Visual Studio:Visual Studio 2010 及以上版本支持部分 C11 特性,…...

flutter开发实战-图片保存到相册
flutter开发实战-图片保存到相册。保存相册使用的是image_gallery_saver插件 一、引入image_gallery_saver插件 在pubspec.yaml中引入插件 # 保存图片到相册image_gallery_saver: ^1.7.1# 权限permission_handler: ^10.0.0二、保存到相册的代码 使用image_gallery_saver将图…...

数据结构---栈
(一)栈之基础补充 C语言内存分配 对于一个C语言程序而言,内存空间主要由五个部分组成 代码段(text)、数据段(data)、未初始化数据段(bss),堆(heap) 和 栈(stack) 组成,其中代码段,数据段和BSS段是编译的时候由编译器分配的,而堆和栈是程序运行的时候由系统分配的。布局如…...

【RabbitMQ】golang客户端教程1——HelloWorld
一、介绍 本教程假设RabbitMQ已安装并运行在本机上的标准端口(5672)。如果你使用不同的主机、端口或凭据,则需要调整连接设置。如果你未安装RabbitMQ,可以浏览我上一篇文章Linux系统服务器安装RabbitMQ RabbitMQ是一个消息代理&…...

计算机图形学笔记2-Viewing 观测
观测主要解决的问题是如何把物体的三维“模型”变成我们在屏幕所看到的二维“图片”,我们在计算机看到实体模型可以分成这样几步: 相机变换(camera transformation)或眼变换(eye transformation):想象把相机放在任意一个位置来观测物体&#…...
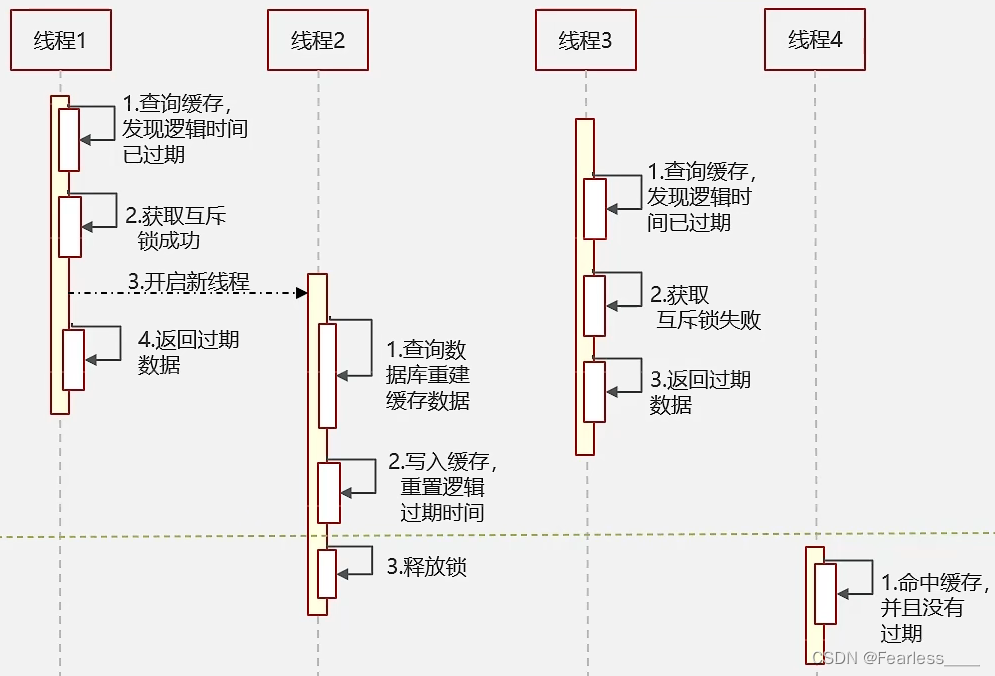
Redis - 三大缓存问题(穿透、击穿、雪崩)
缓存穿透 概念: 查询一个数据库中也不存在的数据,数据库查询不到数据也就不会写入缓存,就会导致一直查询数据库 解决方法: 1. 缓存空数据 如果数据库也查询不到,就把空结果进行缓存 缺点是 - 消耗内存 2. 使用布…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
