代码随想录算法训练营day49
文章目录
- Day49
- 买卖股票的最佳时机
- 题目
- 思路
- 代码
- 贪心算法
- 动态规划法(推荐)
- 买卖股票的最佳时机II
- 题目
- 思路
- 代码
Day49
买卖股票的最佳时机
121. 买卖股票的最佳时机 - 力扣(LeetCode)
题目
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
- 示例 1:
- 输入:[7,1,5,3,6,4]
- 输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。 - 示例 2:
- 输入:prices = [7,6,4,3,1]
- 输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
思路
动规五部曲
- 确定dp数组以及下标含义
dp[i][0] 表示第i天持有股票所得最多现金 ,这里可能有同学疑惑,本题中只能买卖一次,持有股票之后哪还有现金呢?
其实一开始现金是0,那么加入第i天买入股票现金就是 -prices[i], 这是一个负数。
dp[i][1] 表示第i天不持有股票所得最多现金
注意这里说的是“持有”,“持有”不代表就是当天“买入”!也有可能是昨天就买入了,今天保持持有的状态
- 确定推导公式
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
- 第i天买入股票,所得现金就是买入今天的股票后所得现金即:-prices[i]
那么dp[i][0]应该选所得现金最大的,所以dp[i][0] = max(dp[i - 1][0], -prices[i]);
如果第i天不持有股票即dp[i][1], 也可以由两个状态推出来
- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
- 第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:prices[i] + dp[i - 1][0]
同样dp[i][1]取最大的,dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
- dp数组的初始化方式
由递推公式 dp[i][0] = max(dp[i - 1][0], -prices[i]); 和 dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);可以看出
其基础都是要从dp[0][0]和dp[0][1]推导出来。
那么dp[0][0]表示第0天持有股票,此时的持有股票就一定是买入股票了,因为不可能有前一天推出来,所以dp[0][0] -= prices[0];
dp[0][1]表示第0天不持有股票,不持有股票那么现金就是0,所以dp[0][1] = 0;
- 如何遍历dp数组
从递推公式可以看出dp[i]都是由dp[i - 1]推导出来的,那么一定是从前向后遍历。
- 举例推导dp数组
代码
贪心算法
class Solution {public int maxProfit(int[] prices) {// 找到一个最小的购入点int low = Integer.MAX_VALUE;// res不断更新,直到数组循环完毕int res = 0;for(int i = 0; i < prices.length; i++){low = Math.min(prices[i], low);res = Math.max(prices[i] - low, res);}return res;}
}
动态规划法(推荐)
class Solution {public int maxProfit(int[] prices) {int dp[][] = new int[prices.length][2];// 0是持有股票所得最多现金,1是不持有股票所得最多现金dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1; i < prices.length; i++){// 持有股票有两种情况,之前买入,刚买入(因为初始资金为0)dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);// 不持有股票有两种情况,之前就不持有,刚卖出dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);}return dp[prices.length - 1][1];}
}
买卖股票的最佳时机II
122. 买卖股票的最佳时机 II - 力扣(LeetCode)
题目
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
- 示例 1:
- 输入: [7,1,5,3,6,4]
- 输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。 - 示例 2:
- 输入: [1,2,3,4,5]
- 输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。 - 示例 3:
- 输入: [7,6,4,3,1]
- 输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
- 1 <= prices.length <= 3 * 10 ^ 4
- 0 <= prices[i] <= 10 ^ 4
思路
在动规五部曲中,这个区别主要是体现在递推公式上,其他都和121. 买卖股票的最佳时机 (opens new window)一样一样的。
dp数组的含义:
- dp[i][0] 表示第i天持有股票所得现金。
- dp[i][1] 表示第i天不持有股票所得最多现金
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
- 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即:dp[i - 1][1] - prices[i]
注意这里和121. 买卖股票的最佳时机 (opens new window)唯一不同的地方,就是推导dp[i][0]的时候,第i天买入股票的情况。
在121. 买卖股票的最佳时机 (opens new window)中,因为股票全程只能买卖一次,所以如果买入股票,那么第i天持有股票即dp[i][0]一定就是 -prices[i]。
而本题,因为一只股票可以买卖多次,所以当第i天买入股票的时候,所持有的现金可能有之前买卖过的利润。
那么第i天持有股票即dp[i][0],如果是第i天买入股票,所得现金就是昨天不持有股票的所得现金 减去 今天的股票价格 即:dp[i - 1][1] - prices[i]。
再来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
- 第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:prices[i] + dp[i - 1][0]
代码
class Solution {public int maxProfit(int[] prices) {int dp[][] = new int[prices.length][2];// 0是持有股票所得最多现金,1是不持有股票所得最多现金dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1; i < prices.length; i++){dp[i][0] = Math.max(dp[i - 1][1] - prices[i], dp[i - 1][0]);dp[i][1] = Math.max(dp[i - 1][0] + prices[i], dp[i - 1][1]);}return dp[prices.length - 1][1];}
}class Solution {public int maxProfit(int[] prices) {int dp[][] = new int [2][2];//dp[i][0]: holding the stock//dp[i][1]: not holding the stockdp[0][0] = - prices[0];dp[0][1] = 0;for(int i = 1; i < prices.length; i++){dp[i % 2][0] = Math.max(dp[(i - 1) % 2][0], dp[(i - 1) % 2][1] - prices[i]);dp[i % 2][1] = Math.max(dp[(i - 1) % 2][1], dp[(i - 1) % 2][0] + prices[i]);}return dp[(prices.length - 1) % 2][1];}
}
相关文章:

代码随想录算法训练营day49
文章目录 Day49买卖股票的最佳时机题目思路代码贪心算法动态规划法(推荐) 买卖股票的最佳时机II题目思路代码 Day49 买卖股票的最佳时机 121. 买卖股票的最佳时机 - 力扣(LeetCode) 题目 给定一个数组 prices ,它的第 i 个元素 prices[i]…...

云计算与大数据——部署Kubernetes集群+完成nginx部署(超级详细!)
云计算与大数据——部署Kubernetes集群完成nginx部署(超级详细!) 部署 Kubernetes 集群的基本思路如下: 准备环境: 选择适合的操作系统:根据需求选择适合的 Linux 发行版作为操作系统,并确保在所有节点上进行相同的选…...
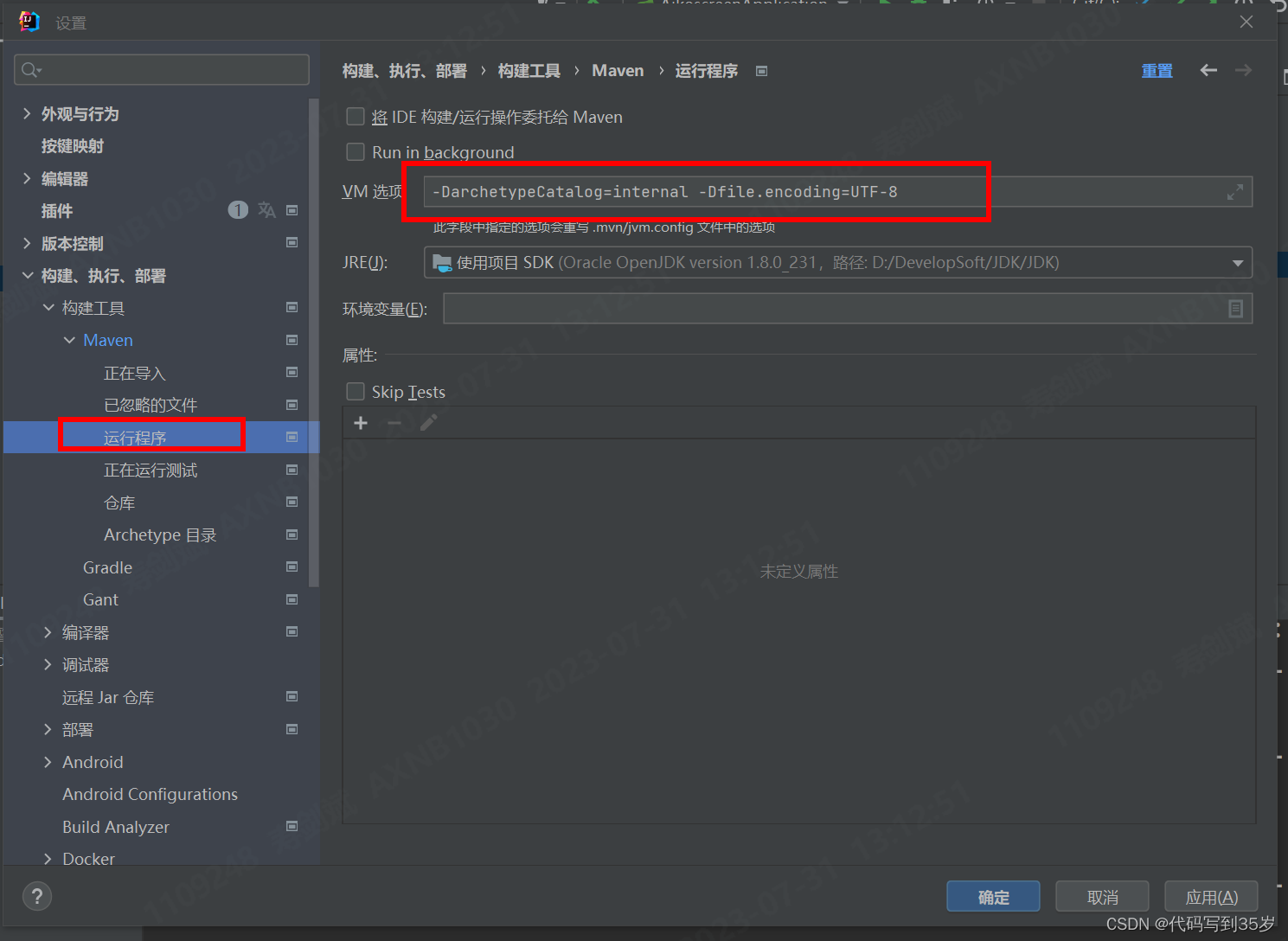
Maven 打包项目后,接口识别中文乱码
背景 项目在Idea里面运行,调用接口发送中文消息正常,用Maven打包项目后,运行jar包,调用接口发送中文出现乱码。 解决方法 1.Idea编译配置 2.如果更改了上述配置之后还是没有效果,则在运行jar包的前面加上 -Dfile.en…...

计算机视觉项目中的文件批量操作与文件批量预处理
计算机视觉项目中的文件批量操作与文件批量预处理 目录 数据集制作文件批量重命名文件批量移动将文件批量按照一定格式进行重命名修改xml文件内容的方法 引言 在计算机视觉项目中,文件批量操作和文件批量预处理是必不可少的步骤。它们涉及处理大量的图像文件&am…...
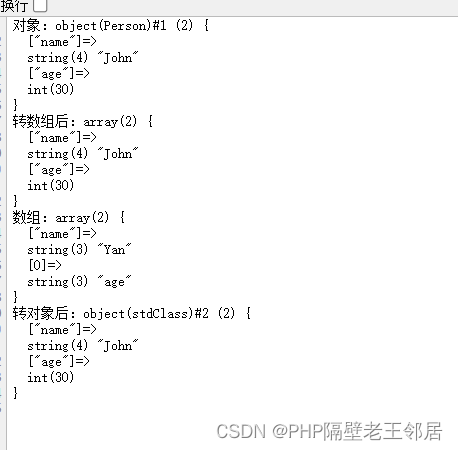
PHP数组转对象和对象转数组
PHP数组转对象和对象转数组 <?php function array_to_object($arr){$obj new stdClass();foreach ($arr as $key > $val) {if (is_array($val) || is_object($val)) {$obj->$key array_to_object($val);} else {$obj->$key $val;}}return $obj; } function o…...

前后端分离开发中的传参
1.post请求,后台代码使用RequestBody注解接收前端传过来的参数 PostMapping("/saveHosp") public Result SaveHosp(RequestBody HospitalSet hospitalSet){//此处省略中间代码......} 此时前端传过来的参数须为JSON格式,前端VUE传参数为&…...

mount: wrong fs type, bad option, bad superblock报错 ubuntu
问题描述 mount: wrong fs type, bad option, bad superblock Ubuntu无法挂载磁盘。 原因 很大概率是你的硬盘是NTFS。 解决 sudo apt install ntfs-3g即可。...
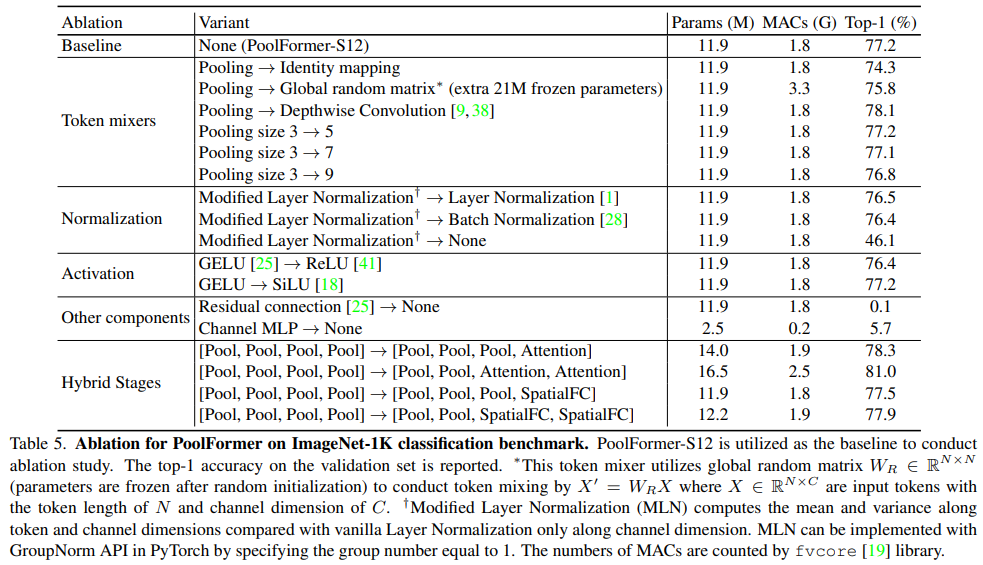
【图像分类】CNN+Transformer结合系列.3
介绍两篇图像分类的论文:ResMLP(arXiv2305),MetaFormer(CVPR2022),两者都与Transformer有关系,前者基于transformer结构的特点设计ResMLP,后者认为宏观架构才是Transform…...
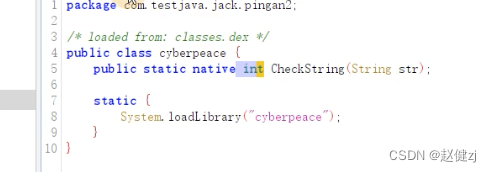
IDA分析实例android_crackme/EasyJNI/Transformers/pingan2
文章目录 第一个实例android_crackme将32位的android_server放到手机目录下给android_server赋予root更改root用户组运行android_serverpc端端口转发安装apk,并运行app打开32位IDA并attach到进程先使用jadx看java层逻辑定位要分析的方法IDA 给两个方法打断点 第二个…...
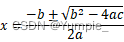
拿捏--->求一元二次方程的根
文章目录 题目描述算法思路代码示例 题目描述 从键盘输入a, b, c的值,编程计算并输出一元二次方程ax2 bx c 0的根,当a 0时,输出“Not quadratic equation”,当a ≠ 0时,根据△ b2 - 4ac的三种情况计算并输出方程…...

深入浅出之Docker Compose详解
目录 1.Docker Compose概述 1.1 Docker Compose 定义 1.2 Docker Compose产生背景 1.3 Docker Compose 核心概念 1.4 Docker Compose 使用步骤 1.5 Docker Compose 常用命令 2. Docker Compose 实战 2.1 Docker Compose下载和卸载 2.2 Docker Compose 项目概述 2.3 Do…...
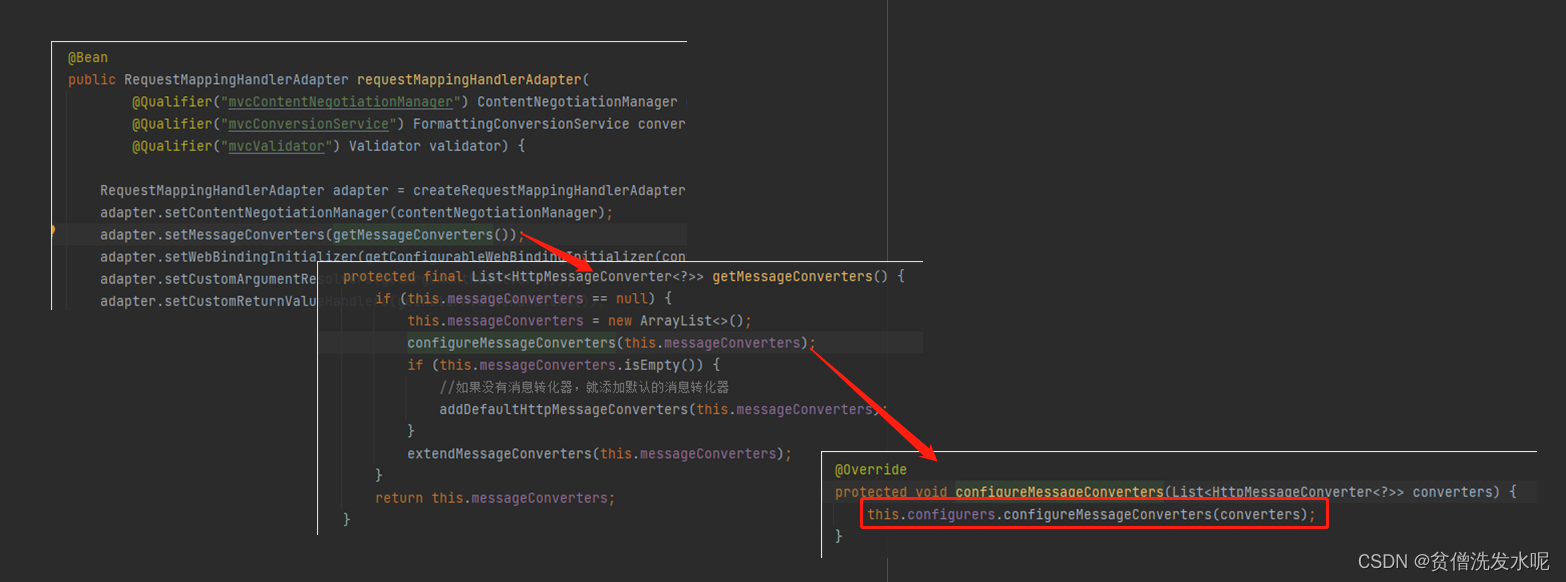
spring5源码篇(12)——spring-mvc请求流程
spring-framework 版本:v5.3.19 文章目录 一、请求流程1、处理器映射器1.1、 RequestMappingHandlerMapping1.2、获取对应的映射方法1.3、添加拦截器 2、获取合适的处理器适配器3、通过处理器适配器执行处理器方法3.1、拦截器的前置后置3.2、处理器的执行3.2.1 参数…...
风辞远的科技茶屋:来自未来的信号枪
很久之前,有位朋友问我,现在科技资讯这么发达了,你们还写啊写做什么呢? 我是这么看的。最终能够凝结为资讯的那个新闻点,其实是一系列事情最终得出的结果,而这个结果又会带来更多新的结果。其中这些“得出”…...

MongoDB教程-8
ObjectId 在之前的所有章节中,我们一直在使用MongoDB的Object Id。在本章中,我们将了解ObjectId的结构。 ObjectId是一个12字节的BSON类型,具有以下结构-- 1. 前4个字节代表自unix epoch以来的秒数 接下来的3个字节是机器标识符 接下来的2…...

Redis 理论部分
前面写了很多redis项目,今天在通过redis的理论加深redis的了解,顺便做个总结 Redis 理论部分 1.redis 速度快的原因 纯内存操作单线程操作,避免频繁的上下文切换以及资源争用的问题,多线程需要占用更多的cpu资源采用非阻塞I/O多…...

Android—Monkey用法
文章目录 Monkey知识 Monkey知识 介绍 Monkey是Android中的一个命令行工具,可以运行在模拟器里或实际设备中。它向系统发送伪随机的用户事件流(如按键输入、触摸屏输入、手势输入等),实现对正在开发的应用程序进行压力测试。Monkey测试是一种为了测试软…...

几个影响 cpu cache 性能因素及 cache 测试工具介绍
》内核新视界文章汇总《 文章目录 1 cache 性能及影响因素1.1 内存访问和性能比较1.2 cache line 对性能的影响1.3 L1 和 L2 缓存大小1.4 指令集并行性对 cache 性能的影响1.5 缓存关联性对 cache 的影响1.6 错误的 cacheline 共享 (缓存一致性)1.7 硬件设计 2 cpu cache benc…...
Java从入门到精通(二)· 基本语法
Java从入门到精通(二) 基本语法 一 变量 1.字面量 计算机是用来处理数据的,字面量就是告诉程序员:数据在程序中的书写格式。 特殊的字符: \n 表示换行, \t 表示一个制表符,即一个tab 2.变量…...
之 面向云原生环境的安全体系)
云安全攻防(三)之 面向云原生环境的安全体系
面向云原生环境的安全体系 根据云原生环境的构成,面向云原生环境的安全体系可包含三个层面的安全体制,它们分别是容器安全、编排系统安全和云原生应用安全,下面,我们逐步来讲解这三点: 容器安全 容器环境࿰…...
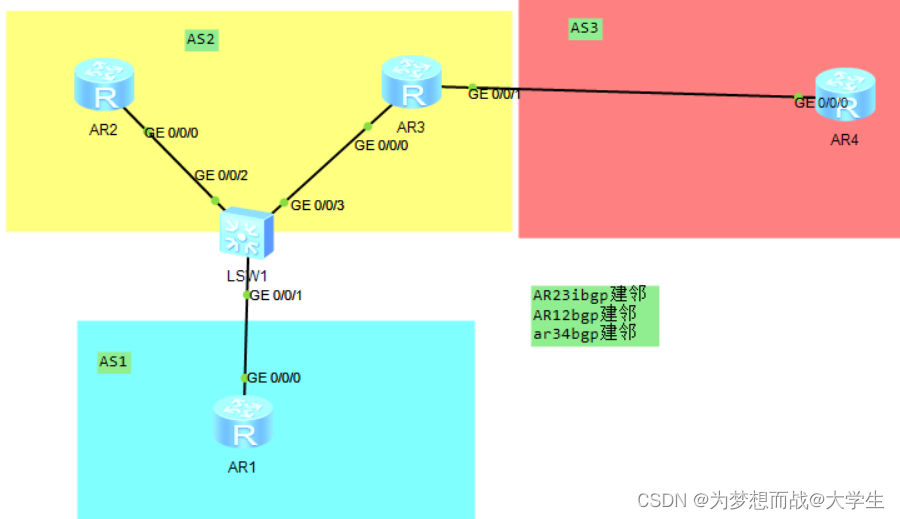
BGP汇总和破解水平分割
一,BGP的宣告问题 在BGP协议中每台运行BGP的设备上,宣告本地直连路由在BGP协议中运行BGP协议的设备来宣告,通过IGP学习到的,未运行BGP协议设备产生的路由; 在BGP协议中宣告本地路由表中路由条目时,将携带本…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
