拿捏--->求一元二次方程的根
文章目录
- 题目描述
- 算法思路
- 代码示例
题目描述
从键盘输入a, b, c的值,编程计算并输出一元二次方程ax2 + bx + c = 0的根,当a = 0时,输出“Not quadratic equation”,当a ≠ 0时,根据△ = b2 - 4ac的三种情况计算并输出方程的根。
输入描述:
多组输入,一行,包含三个浮点数a, b, c,以一个空格分隔,表示一元二次方程ax2 + bx + c = 0的系数。
输出描述:
针对每组输入,输出一行,输出一元二次方程ax2 + bx +c = 0的根的情况。
如果a = 0,输出“Not quadratic equation”;
如果a ≠ 0,分三种情况:
△ = 0,则两个实根相等,输出形式为:x1=x2=…。
△ > 0,则两个实根不等,输出形式为:x1=…;x2=…,其中x1 <= x2。
△ < 0,则有两个虚根,则输出:x1=实部-虚部i;x2=实部+虚部i,即x1的虚部系数小于等于x2的虚部系数,实部为0时不可省略。实部= -b / (2a),虚部= sqrt(-△ ) / (2a)所有实数部分要求精确到小数点后2位,数字、符号之间没有空格。
算法思路
要想使用c语言编写这个实例,就需要知道数学上的公式。
一元二次方程表达式为:a * x * x + bx + c = 0(其中,a ≠ 0)
根的判别式为:Δ = b * b - 4 * a * c;
求根公式为:
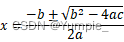
手动输入三个系数,分别代表二次项系数、一次项系数、常数项;
判断输入的二次项系数是否为0,如果为0,提示“输入的第一个值不合法,请重新输入!”;
如果二次项系数不为0,利用根的判别式,计算一元二次方程是否有根;
如果判别式 Δ >= 0 ,代表方程有两个根,输出根;
如果 Δ < 0 ,提示“方程无根”。
代码示例
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<math.h>
int main()
{float a, b, c;while (scanf("%f %f %f", &a, &b, &c) != EOF){double dt = pow(b, 2) - 4 * a * c;if (a == 0){printf("Not quadratic equation");}else{if (dt == 0)//△=0{double x1 = (-b - sqrt(dt)) / (2 * a);double x2 = (-b + sqrt(dt)) / (2 * a);printf("x1=x2=%.2f", x1);}else if (dt > 0)//△>0{double x1 = (-b - sqrt(dt)) / (2 * a);double x2 = (-b + sqrt(dt)) / (2 * a);printf("x1=%.2f;x2=%.2f", x1, x2);}else//△<0{double real = (-b) / (2 * a);//实部double imaginary = sqrt(-dt) / (2 * a);//虚部printf("x1=%.2f-%.2fi;x2=%.2f+%.2fi", real, imaginary, real, imaginary);}}printf("\n");}return 0;
}相关文章:
拿捏--->求一元二次方程的根
文章目录 题目描述算法思路代码示例 题目描述 从键盘输入a, b, c的值,编程计算并输出一元二次方程ax2 bx c 0的根,当a 0时,输出“Not quadratic equation”,当a ≠ 0时,根据△ b2 - 4ac的三种情况计算并输出方程…...

深入浅出之Docker Compose详解
目录 1.Docker Compose概述 1.1 Docker Compose 定义 1.2 Docker Compose产生背景 1.3 Docker Compose 核心概念 1.4 Docker Compose 使用步骤 1.5 Docker Compose 常用命令 2. Docker Compose 实战 2.1 Docker Compose下载和卸载 2.2 Docker Compose 项目概述 2.3 Do…...
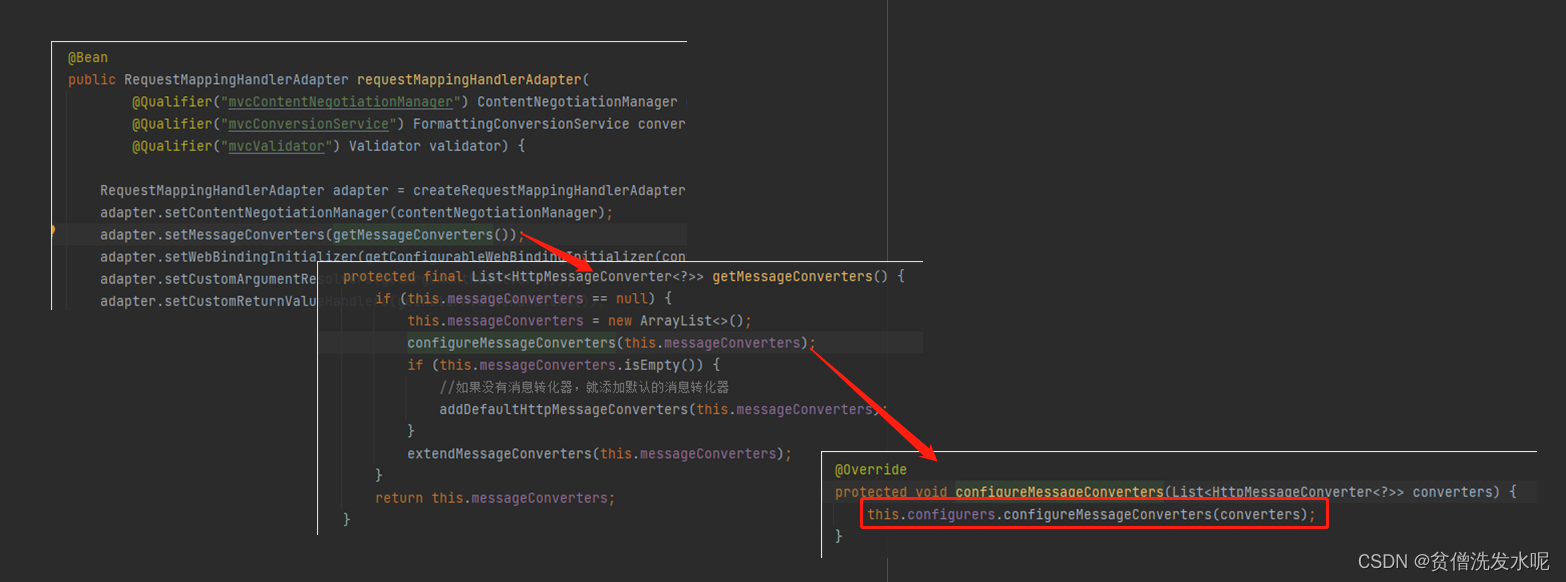
spring5源码篇(12)——spring-mvc请求流程
spring-framework 版本:v5.3.19 文章目录 一、请求流程1、处理器映射器1.1、 RequestMappingHandlerMapping1.2、获取对应的映射方法1.3、添加拦截器 2、获取合适的处理器适配器3、通过处理器适配器执行处理器方法3.1、拦截器的前置后置3.2、处理器的执行3.2.1 参数…...
风辞远的科技茶屋:来自未来的信号枪
很久之前,有位朋友问我,现在科技资讯这么发达了,你们还写啊写做什么呢? 我是这么看的。最终能够凝结为资讯的那个新闻点,其实是一系列事情最终得出的结果,而这个结果又会带来更多新的结果。其中这些“得出”…...

MongoDB教程-8
ObjectId 在之前的所有章节中,我们一直在使用MongoDB的Object Id。在本章中,我们将了解ObjectId的结构。 ObjectId是一个12字节的BSON类型,具有以下结构-- 1. 前4个字节代表自unix epoch以来的秒数 接下来的3个字节是机器标识符 接下来的2…...

Redis 理论部分
前面写了很多redis项目,今天在通过redis的理论加深redis的了解,顺便做个总结 Redis 理论部分 1.redis 速度快的原因 纯内存操作单线程操作,避免频繁的上下文切换以及资源争用的问题,多线程需要占用更多的cpu资源采用非阻塞I/O多…...

Android—Monkey用法
文章目录 Monkey知识 Monkey知识 介绍 Monkey是Android中的一个命令行工具,可以运行在模拟器里或实际设备中。它向系统发送伪随机的用户事件流(如按键输入、触摸屏输入、手势输入等),实现对正在开发的应用程序进行压力测试。Monkey测试是一种为了测试软…...

几个影响 cpu cache 性能因素及 cache 测试工具介绍
》内核新视界文章汇总《 文章目录 1 cache 性能及影响因素1.1 内存访问和性能比较1.2 cache line 对性能的影响1.3 L1 和 L2 缓存大小1.4 指令集并行性对 cache 性能的影响1.5 缓存关联性对 cache 的影响1.6 错误的 cacheline 共享 (缓存一致性)1.7 硬件设计 2 cpu cache benc…...
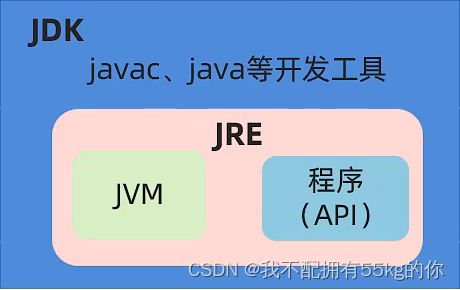
Java从入门到精通(二)· 基本语法
Java从入门到精通(二) 基本语法 一 变量 1.字面量 计算机是用来处理数据的,字面量就是告诉程序员:数据在程序中的书写格式。 特殊的字符: \n 表示换行, \t 表示一个制表符,即一个tab 2.变量…...
之 面向云原生环境的安全体系)
云安全攻防(三)之 面向云原生环境的安全体系
面向云原生环境的安全体系 根据云原生环境的构成,面向云原生环境的安全体系可包含三个层面的安全体制,它们分别是容器安全、编排系统安全和云原生应用安全,下面,我们逐步来讲解这三点: 容器安全 容器环境࿰…...
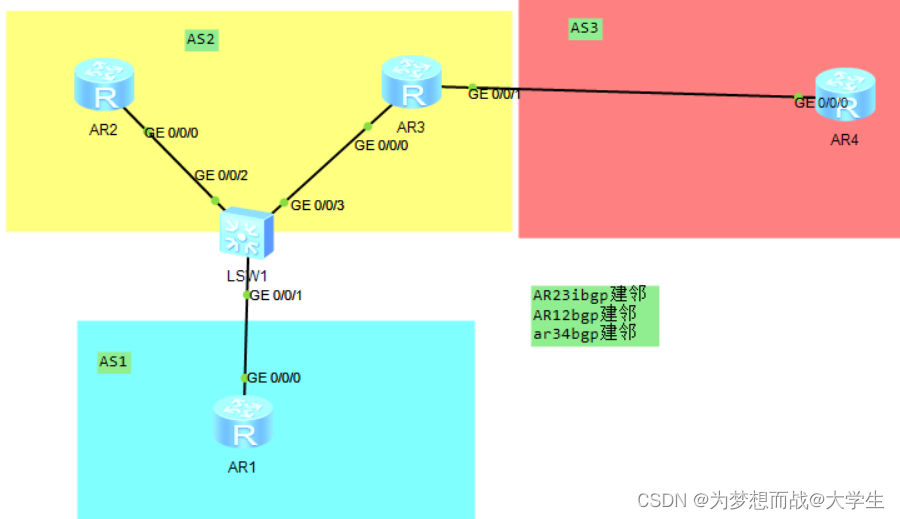
BGP汇总和破解水平分割
一,BGP的宣告问题 在BGP协议中每台运行BGP的设备上,宣告本地直连路由在BGP协议中运行BGP协议的设备来宣告,通过IGP学习到的,未运行BGP协议设备产生的路由; 在BGP协议中宣告本地路由表中路由条目时,将携带本…...
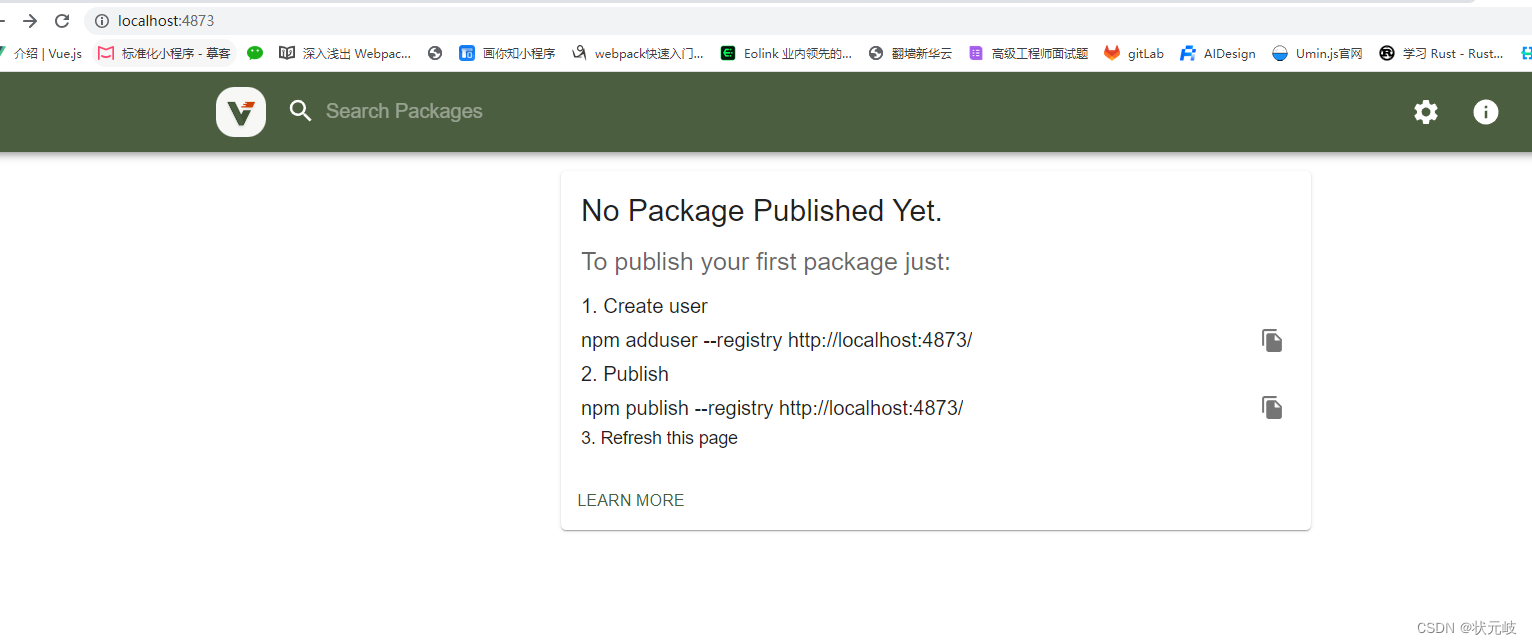
BUG:pm2启动verdaccio报错:Invalid or unexpected toke
输入命令: pm2 state verdaccio 问题描述: pm2 logs verdaccio报错翻译:数据格式错误 导致我呢提原因,没有找到运行文件, 发现问题:因为命令默认查找verdaccio是去系统盘查找。 解决方式 1:…...

Zookeeper笔记
为什么要使用Zookeeper dubbo需要一个注册中心,而Zookeeper是我们在使用Dubbo是官方推荐的注册中心 Zookeeper介绍 Zookeeper的集群机制 Zookeeper是为了其他分布式程序提供服务的,所以不能随便就挂了。Zookeeper的集群机制采取的是半数存活机制。也…...
【视觉SLAM入门】5.1. 特征提取和匹配--FAST,ORB(关键点描述子),2D-2D对极几何,本质矩阵,单应矩阵,三角测量,三角化矛盾
"不言而善应" 0. 基础知识1. 特征提取和匹配1.1 FAST关键点1.2 ORB的关键点--改进FAST1.3 ORB的描述子--BRIEF1.4 总结 2. 对极几何,对极约束2.1 本质矩阵(对极约束)2.1.1 求解本质矩阵2.1.2 恢复相机运动 R , t R,t R,…...

【能量管理系统( EMS )】基于粒子群算法对光伏、蓄电池等分布式能源DG进行规模优化调度研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
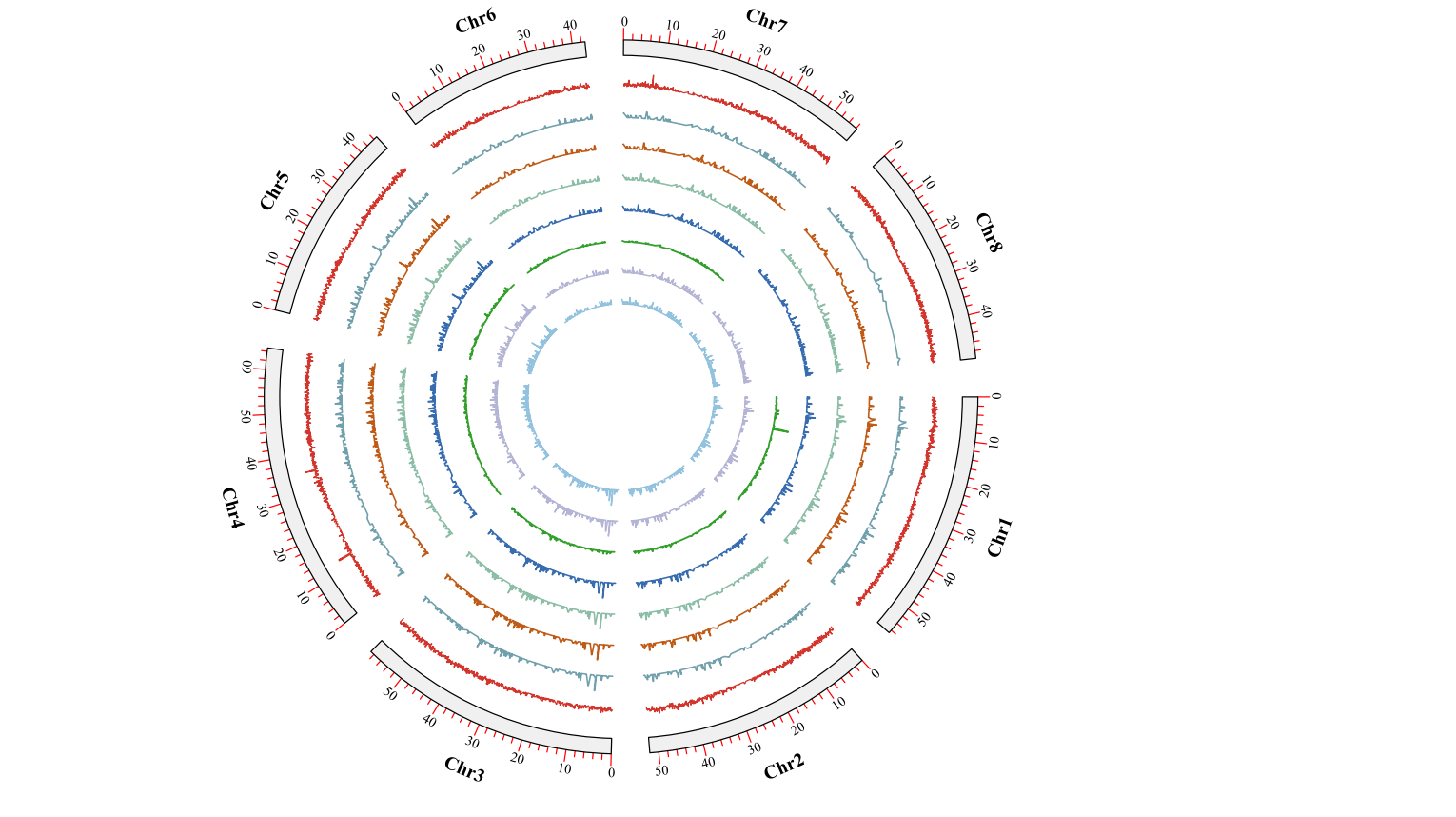
绘制Circos基因圈图
写在前面 昨天在绘制Circos圈图,已经隔了2年左右没有做这类的图了。这时间过得真是快,但是文章和成果依旧是没有很明显的成效。只能安慰自己,后面的时间继续加油吧!关于Cirocs图的制作,我从刚开始到现在都是是使用TBt…...

openGauss学习笔记-26 openGauss 高级数据管理-约束
文章目录 openGauss学习笔记-26 openGauss 高级数据管理-约束26.1 NOT NULL约束26.2 UNIQUE约束26.3 PRIMARY KEY26.4 FOREIGN KEY26.5 CHECK约束 openGauss学习笔记-26 openGauss 高级数据管理-约束 约束子句用于声明约束,新行或者更新的行必须满足这些约束才能成…...

学习React(四)
学习React(四) componentWillMount(被放弃使用)rendercomponentDidMountshouldComponentUpdate(nextProps,nextState)componentWillUpdate(被放弃使用)componentDidUpdatecomponentWillReceiveProps&#x…...

如何将单体项目拆分成微服务
1、如何将单体项目拆分成微服务 如何拆分微服务?其实对不同的业务项目场景,对应有不同的拆分方案。需要项目人员详细的分析项目需求、团队现状、业务边界、业务逻辑等方方面面,拆分的粒度既不能过细,也不能过粗,需要把…...
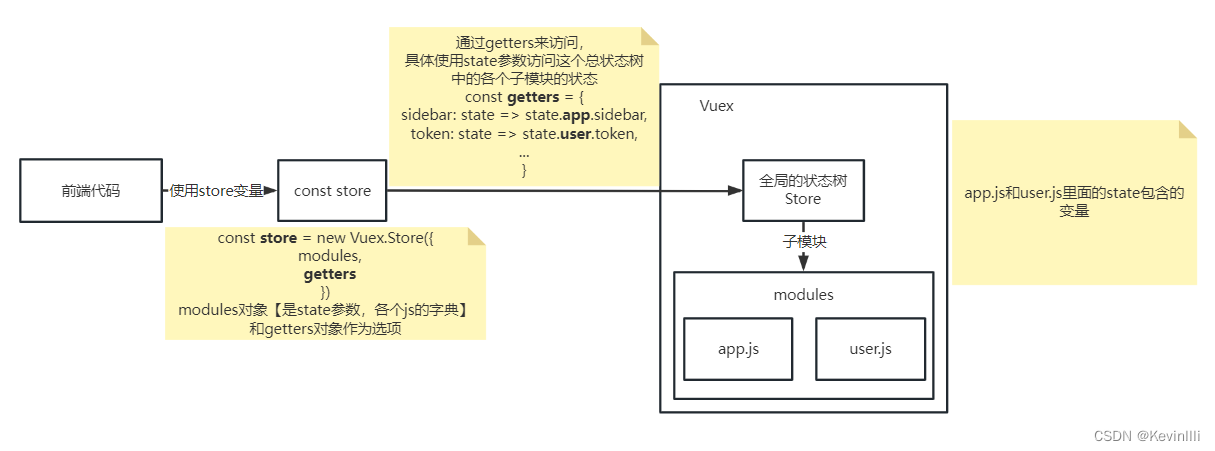
【Vue框架】Vuex状态管理
前言 在上一篇 【Vue框架】Vue路由配置 结尾时说到store.js,在代码里new Vuex.Store()传入了getters对象;本篇专门针对getters的内容进行整理。 1、getters.js 1.1 代码 // 用于存储获取状态的方法 const getters {// 这里的state参数,是…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
