【视觉SLAM入门】5.1. 特征提取和匹配--FAST,ORB(关键点描述子),2D-2D对极几何,本质矩阵,单应矩阵,三角测量,三角化矛盾
"不言而善应"
- 0. 基础知识
- 1. 特征提取和匹配
- 1.1 FAST关键点
- 1.2 ORB的关键点--改进FAST
- 1.3 ORB的描述子--BRIEF
- 1.4 总结
- 2. 对极几何,对极约束
- 2.1 本质矩阵(对极约束)
- 2.1.1 求解本质矩阵
- 2.1.2 恢复相机运动 R , t R,t R,t
- 2.1.3 本质矩阵调整
- 2.1.3 遗留问题
- 2.2 单应矩阵(特别提一下)
- 2.3 三角测量(Triangulation)---深度信息
为什么重要?我们是在做什么事?
- 特征提取和匹配: 首先是两幅图像的特征提取,然后是对应特征点的匹配。接下来的工作是根据得到的匹配点对,估计相机的运动,具体根据相机分为三种方法:
-
- 单目相机:2D-2D: 对极几何 方法
-
- 双目或者RGBD相机: 3D-3D: ICP 方法
-
- 一个3D点和它相机中的投影位置: 3D-2D : PnP 方法
0. 基础知识
视觉SLAM两阶段:
- 前端(VO) —> 粗略相机运动 ------> 提供给后端初始值
- 后端 —> 优化
VO的实现方法两派:
- 不提取特征点 ----> 直接法
- 提取特征点 ------> 特征点法 ----> 成熟
1. 特征提取和匹配
注意:有些东西的作用你要明白:
- 关键点: 是在一幅图像中找到的点,作用是在一幅图中找到路标点(有代表性的点)。
- 描述子: 在两个图像的关键点找到的情况下,匹配两个图像中的对应关键点。 通常是向量
- 特征点: 由关键点和描述子两部分组成,任务是(提取XXX关键点,计算XXX描述子)
- 尺度不变性: 为了确保从远到近都能检测出来关键点
- 旋转不变性: 为了确保图像旋转后还能检测出来关键点
- 特征提取的是关键点和描述子,特征匹配是根据描述子匹配的
几种图像特征:
- SIFT特征:计算量太大,有些精确
- FAST关键点:没有描述子,最快,不准。
- ORB特征:改进FAST关键点,采用BRIEF描述子
1.1 FAST关键点
-
- 比较周围半径圆范围内的灰度情况,差别大就是角点。
-
- 设定一个数量,比如9,范围内至少有连续9个点和选定点的亮度色差大于阈值T的时候,该点就称为特征点。这种方法叫FAST-9。
-
- 检测完角点扎堆,非极大值抑制
1.2 ORB的关键点–改进FAST
改进了FAST关键点法,克服了缺点:
-
- 可以指定提取数量: 对点分别计算Harris相应,取前N个响应最大的角点;
-
- 尺度不变性: 用图像金字塔提取每一层的角点,均为角点才是角点;
-
- 旋转不变性:灰度质心法,保证图像旋转后还能检测到。最后得到的是角度,从图像光度明指向光度暗的一侧,具体实现如下:

1.3 ORB的描述子–BRIEF
作用:为了保证两个图像中提取出的关键点能对应上各自匹配的点对。
- BRIEF是二进制描述子,描述向量由0和1组成
- 做法:选取关键点周围的图像块,随机选取像素点对(有很多选点方法),如128就是取128个点对,设两个点像素分别为 p , q p, q p,q , 然后计算 p , q p, q p,q 的大小关系,按结果分别记为0,1, 最后得到128位的二进制数。匹配的时候在第二幅图像中也用相同的选点方法,最后比较两幅图像中关键点描述子距离(二进制的字串衡量就是汉明距离)。
1.4 总结
通过图像特征点的对应关系,解决了SLAM最重要的一步:同一个点在不同图像中如何检测出来。
特征匹配的方法有:
- 暴力匹配(Brute-Force Matcher): 第二幅图像中每个点都计算其在第一幅图对应的特征点,运算量大;
- 快速最近邻(FLANN): 适用于匹配点数量多
- 。。。
2. 对极几何,对极约束
目的是求相机运动 R , t R, t R,t,内参一般知道
这是2D-2D的单目情形,假设相机经过一次运动 R , t R, t R,t 后得到的两帧图如下:
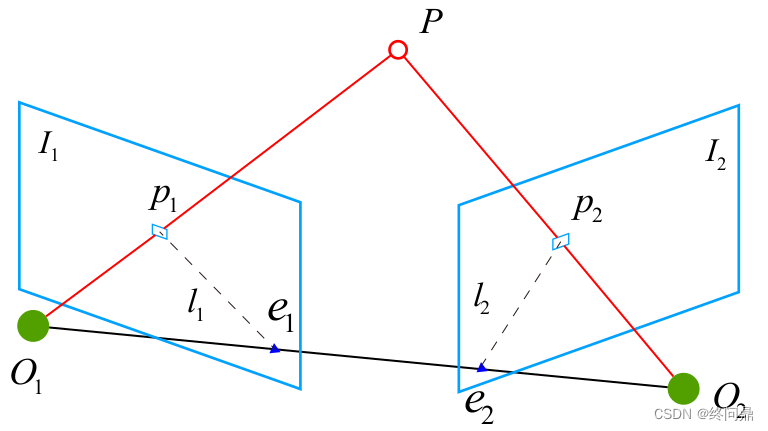
其中点和线定义如下:
- p 1 , p 2 p_1,p_2 p1,p2 : 分别同一个点在两帧下的投影点
- O 1 , O 2 O_1, O_2 O1,O2 : 相机光心
- P P P : 真实世界中的点
- I 1 , I 2 I_1, I_2 I1,I2 : 两帧图像
- O 1 O 2 连线 O_1O_2连线 O1O2连线 : 基线
- e 1 , e 2 e_1, e_2 e1,e2 : O 1 O 2 O_1O_2 O1O2 和 I 1 , I 2 I_1,I_2 I1,I2 的交点,也叫极点
- 极平面 : O 1 , O 2 , P O_1,O_2,P O1,O2,P 所在平面
- 极线 : l 1 , l 2 l_1, l_2 l1,l2 。
如果没有深度信息,则 O 1 P O_1P O1P 直线上任一点投影都在 p 1 p_1 p1,且他在第二帧图像上的轨迹在 极线 p 2 e 2 p_2e_2 p2e2 上,所以有真确的匹配,就可以推断 P P P 的位置,然后得到相机的运动。
2.1 本质矩阵(对极约束)
推理部分略,详见《视觉SLAM十四讲》第七章7.3节,这里给出结果。
仍参考上图,取两个像素点归一化平面上的点 x 1 , x 2 x_1,x_2 x1,x2:
x 1 = K − 1 p 1 , x 2 = K − 1 p 2 x_1=K^{-1}p_1,\qquad\qquad x_2 = K^{-1}p_2 x1=K−1p1,x2=K−1p2
则 最终的对极约束 为:
p 2 T K − T t \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad p_2^TK^{-T}t p2TK−Tt^ R K − 1 p 1 = 0 RK^{-1}p_1 = 0 RK−1p1=0
它的含义是 O 1 , O 2 , P O_1,O_2,P O1,O2,P 三点共面。从式中心部分,记本质矩阵 E \boldsymbol E E 和基础矩阵 F \boldsymbol F F 如下:
E = t \qquad\qquad\qquad\qquad\qquad\qquad\qquad E=t E=t^ R F = K − T E K − 1 x 2 T E x 1 = p 2 T F p 1 = 0 R\qquad\qquad F=K^{-T}EK^{-1}\qquad\qquad x_2^TEx_1=p_2^TFp_1=0 RF=K−TEK−1x2TEx1=p2TFp1=0
可以看出 E \boldsymbol E E 和 F \boldsymbol F F 只差内参 K K K (已知),所以二者 求一即可。
不妨以 E = t E=t E=t^ R R R来求解。则后续工作如下:
- 根据已匹配点对,求出 E \boldsymbol E E或 F \boldsymbol F F
- 根据 E \boldsymbol E E或 F \boldsymbol F F,求出相机运动 R , t \boldsymbol {R,t} R,t
2.1.1 求解本质矩阵
探究本质矩阵的特点:
-
- 由对极约束 x 2 T E x 1 = 0 x_2^TEx_1=0 x2TEx1=0 , 所以它在不同尺度下等价,左右乘依旧满足约束。又因为 E = t E=t E=t^ R R R, 原本有6个自由度,故去掉尺度,还有5个自由度
-
- E 的内在性质 E的内在性质 E的内在性质 : 它的奇异值必定是 [ δ , δ , 0 ] T [\delta ,\delta, 0]^T [δ,δ,0]T 的形式,非线性的性质。
求解依据:
x 2 T E x 1 = 0 ( 1 ) x_2^TEx_1 = 0 \qquad\qquad\qquad\qquad (1) x2TEx1=0(1)
理论上可以用5对点来求解,但是很麻烦。故用 八点法 求解(由于尺度不变性)。
1.首先考虑一对点(归一化坐标 x 1 , x 2 x_1, x_2 x1,x2 ): 将(1)式展开:
( u 1 , v 1 , 1 ) ( e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ) ( u 2 v 2 1 ) = 0 ⇓ 将 e 展开 e = [ e 1 , e 2 , e 3 , e 4 , e 5 , e 6 , e 7 , e 8 , e 9 ] ⇓ 展开并重写 [ u 1 u 2 , u 1 v 2 , u 1 , v 1 u 2 , v 1 v 2 , v 1 , u 2 , v 2 , 1 ] ⋅ e = 0 ⇓ 考虑 8 对点的方程组 (u_1, v_1,1)\begin{pmatrix} e_1\quad e_2\quad e_3 \\e_4\quad e_5\quad e_6 \\e_7\quad e_8\quad e_9 \end{pmatrix}\begin{pmatrix} u_2\\v_2\\1 \end{pmatrix}=0 \quad\\\; \\\;\Downarrow 将e展开 \\\;\\\;e=[e_1,e_2,e_3,e_4,e_5,e_6,e_7,e_8,e_9]\\\;\\\; \Downarrow展开并重写\\\;\\\; [u_1u_2,u_1v_2,u_1,v_1u_2,v_1v_2,v_1,u_2,v_2,1]\cdot e = 0 \\\;\\\Downarrow考虑8对点的方程组 (u1,v1,1) e1e2e3e4e5e6e7e8e9 u2v21 =0⇓将e展开e=[e1,e2,e3,e4,e5,e6,e7,e8,e9]⇓展开并重写[u1u2,u1v2,u1,v1u2,v1v2,v1,u2,v2,1]⋅e=0⇓考虑8对点的方程组

至此,本质矩阵的求解结束
2.1.2 恢复相机运动 R , t R,t R,t
- 对 E \boldsymbol E E 做SVD分解
E = U ∑ V T ( U , V 正交阵, ∑ 为奇异矩阵且 = d i a g ( δ , δ , 0 ) ) E=U\sum V_T\qquad\qquad (U,V正交阵,\sum 为奇异矩阵且=diag(\delta,\delta,0)) E=U∑VT(U,V正交阵,∑为奇异矩阵且=diag(δ,δ,0)) - 求解较为复杂,这里给出结果
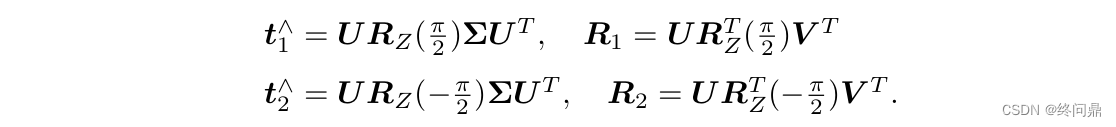 一共存在4组解。如下:
一共存在4组解。如下:
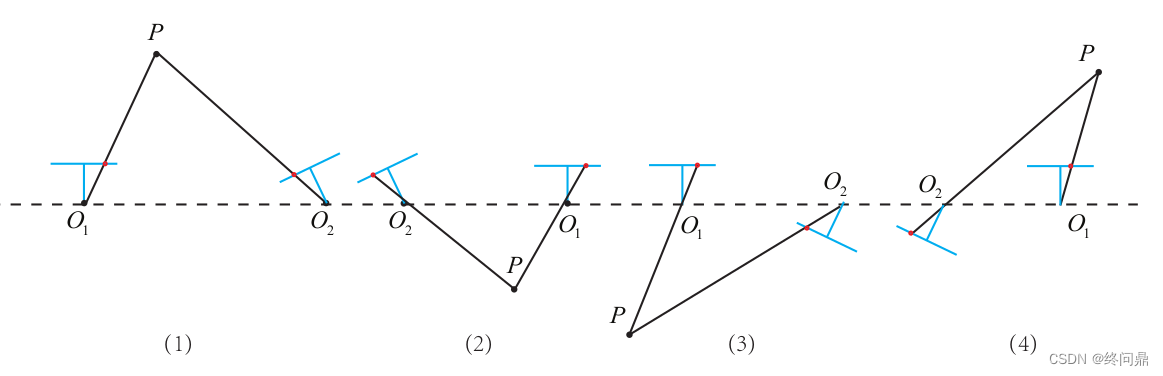
蓝色横线就是相机平面,红色点为投影点。
有(1)满足要求,因为只有这样才符合投影模型,深度才为正。将解出来的解带入验算即可。
2.1.3 本质矩阵调整
5个自由度,用了8个点,上边的方程求解出的 E E E 可能不满足 E E E 的内在性质( ∑ = d i a g ( δ , δ , 0 ) \boldsymbol {\sum = diag(\delta,\delta,0)} ∑=diag(δ,δ,0) ),因此要调整。做法如下:
在做SVD分解时,得到
∑ = d i a g ( δ 1 , δ 2 , δ 3 ) ⇓ 设 δ 1 ≥ δ 2 ≥ δ 3 ,则新的 ∑ 如下 ∑ ′ = d i a g ( δ 1 + δ 2 2 , δ 1 + δ 2 2 , 0 ) ⇓ 带入 S V D 分解式 E = U d i a g ( δ 1 + δ 2 2 , δ 1 + δ 2 2 , 0 ) V T \sum = diag(\delta_1,\delta_2,\delta_3) \\\;\\\Downarrow 设\delta_1\ge\delta_2\ge\delta_3,则新的\sum如下\\\; \\\sum' = diag(\frac{\delta_1+\delta_2}{2}, \frac{\delta_1+\delta_2}{2},0)\\\; \\\Downarrow 带入SVD分解式\\\; \\E=Udiag(\frac{\delta_1+\delta_2}{2}, \frac{\delta_1+\delta_2}{2},0)V^T ∑=diag(δ1,δ2,δ3)⇓设δ1≥δ2≥δ3,则新的∑如下∑′=diag(2δ1+δ2,2δ1+δ2,0)⇓带入SVD分解式E=Udiag(2δ1+δ2,2δ1+δ2,0)VT
相当于把求出来的矩阵投影到了 E \boldsymbol E E 的流形上,也可以直接取 ∑ = ( 1 , 1 , 0 ) \sum = (1,1,0) ∑=(1,1,0) (尺度不变性)
2.1.3 遗留问题
- E \boldsymbol E E 的尺度不确定性导致了 t \boldsymbol {t} t 的尺度不确定性。(由于 R \boldsymbol R R) 自身带有约束。因此单目SLAM存在初始化: 以 t \boldsymbol t t 的单位为固定尺度1的计算相机运动和特征点;
- 单目初始化不能只有纯旋转,必须要有一定的平移: 因为 t \boldsymbol t t 为0,所以 E \boldsymbol E E 最终也为0;
- 当点多于8对,此时构成超定方程,我们有两种做法:
- 3.1. 最小化一个二次型(最小二乘意义下的)
- 3.2. 随机采样一致性(RANSAC),可以处理有错误匹配的情况,一般用这个。
2.2 单应矩阵(特别提一下)
为什么需要单应矩阵 H H H (Homography)?
- 当特征点共面,相机纯旋转, F \boldsymbol F F 的自由度少了 t t t ,下降。这就是退化现象。
- 如果这时仍用八点法求解,多出来的自由度是噪声带来的。
- 为了避免退化,同时估计基础矩阵 F \boldsymbol F F 和 单应矩阵 H \boldsymbol H H,选择重投影误差小的矩阵作为最终运动估计矩阵。
故 H H H 假设的所有特征点位于平面上。
详细推导内容见SLAM十四讲7.3.3 。根据法平面做的,求解与 E 和 F E和F E和F 相似。只需要4对匹配点就可以算出。
2.3 三角测量(Triangulation)—深度信息
-
计算深度:回想相机模型那一节,这里的深度就是之前被我们固定为1的 s \boldsymbol s s 。以第一帧图像为坐标原点,由以上对极约束内容有:
s 1 x 1 = s 2 R x 2 + t ⇓ 分别单独计算,左乘 x 1 的反对称矩阵 s_1x_1 = s_2Rx_2+t \\\; \\\Downarrow 分别单独计算,左乘x_1的反对称矩阵 s1x1=s2Rx2+t⇓分别单独计算,左乘x1的反对称矩阵
s 1 ( x 1 \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad s_1(x_1 s1(x1^ ) x 1 = 0 = s 2 ( x 1 )x_1=0=s_2(x_1 )x1=0=s2(x1 ^ ) R x 2 + ( x 1 )\;Rx_2+(x_1 )Rx2+(x1 ^ ) t )t )t -
可以直接求得深度 s 1 , s 2 \boldsymbol {s_1,s_2} s1,s2 。但是由于噪声的存在,我们一般是求最小二乘解,而不是零解。同样由于尺度不确定性,我们只知道深度对于t的数量,而不知道具体究竟是多少米。
-
三角化矛盾: 平移越大三角化越精确,但是视野越短,反之亦然。
相关文章:

【视觉SLAM入门】5.1. 特征提取和匹配--FAST,ORB(关键点描述子),2D-2D对极几何,本质矩阵,单应矩阵,三角测量,三角化矛盾
"不言而善应" 0. 基础知识1. 特征提取和匹配1.1 FAST关键点1.2 ORB的关键点--改进FAST1.3 ORB的描述子--BRIEF1.4 总结 2. 对极几何,对极约束2.1 本质矩阵(对极约束)2.1.1 求解本质矩阵2.1.2 恢复相机运动 R , t R,t R,…...

【能量管理系统( EMS )】基于粒子群算法对光伏、蓄电池等分布式能源DG进行规模优化调度研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
绘制Circos基因圈图
写在前面 昨天在绘制Circos圈图,已经隔了2年左右没有做这类的图了。这时间过得真是快,但是文章和成果依旧是没有很明显的成效。只能安慰自己,后面的时间继续加油吧!关于Cirocs图的制作,我从刚开始到现在都是是使用TBt…...

openGauss学习笔记-26 openGauss 高级数据管理-约束
文章目录 openGauss学习笔记-26 openGauss 高级数据管理-约束26.1 NOT NULL约束26.2 UNIQUE约束26.3 PRIMARY KEY26.4 FOREIGN KEY26.5 CHECK约束 openGauss学习笔记-26 openGauss 高级数据管理-约束 约束子句用于声明约束,新行或者更新的行必须满足这些约束才能成…...

学习React(四)
学习React(四) componentWillMount(被放弃使用)rendercomponentDidMountshouldComponentUpdate(nextProps,nextState)componentWillUpdate(被放弃使用)componentDidUpdatecomponentWillReceiveProps&#x…...

如何将单体项目拆分成微服务
1、如何将单体项目拆分成微服务 如何拆分微服务?其实对不同的业务项目场景,对应有不同的拆分方案。需要项目人员详细的分析项目需求、团队现状、业务边界、业务逻辑等方方面面,拆分的粒度既不能过细,也不能过粗,需要把…...
【Vue框架】Vuex状态管理
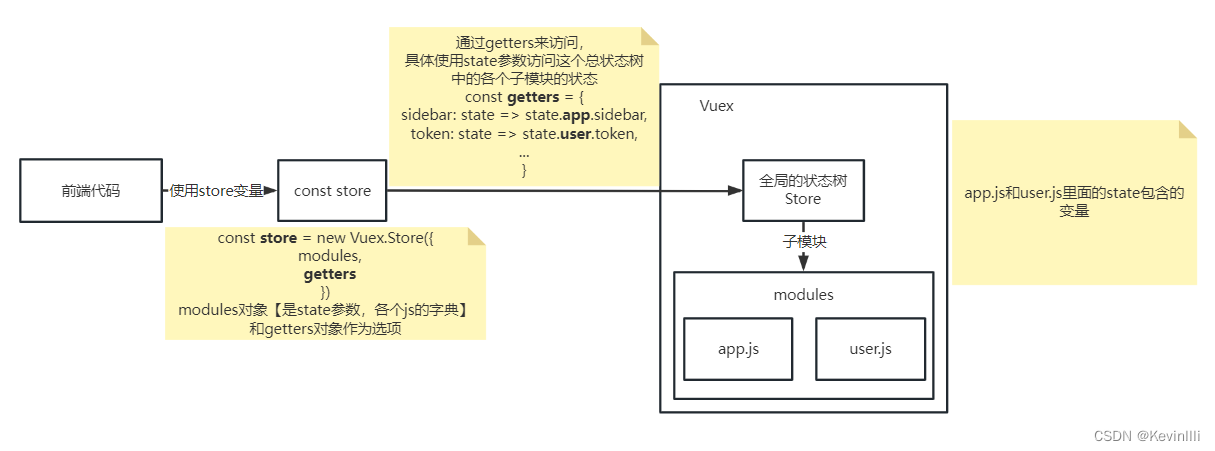
前言 在上一篇 【Vue框架】Vue路由配置 结尾时说到store.js,在代码里new Vuex.Store()传入了getters对象;本篇专门针对getters的内容进行整理。 1、getters.js 1.1 代码 // 用于存储获取状态的方法 const getters {// 这里的state参数,是…...
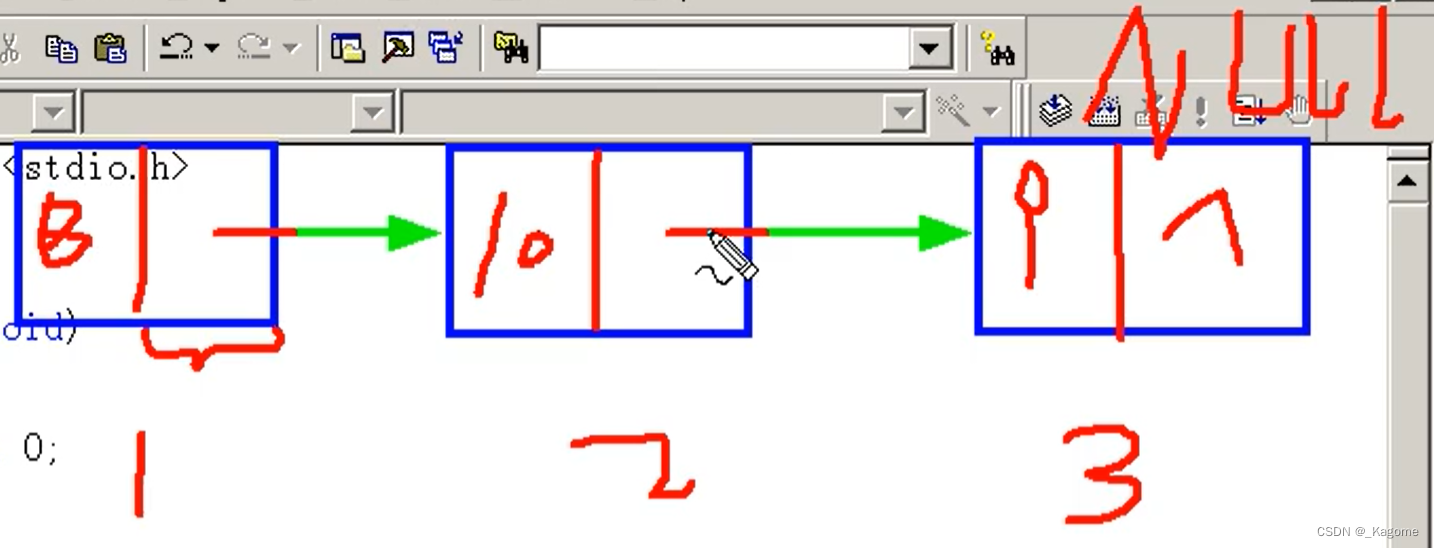
Linked List
文章目录 链表定义专业术语代码链表分类常见算法链表创建和常用算法 链表总结 链表 补充知识 typedef 给类型换名字,比如 typedef struct Student {int sid;char name[100];char sex; }ST;//ST就代表了struct Student //即这上方一大坨都可以用ST表示 //原先结构体…...

javascript数组基础
文章和代码已经归档至【Github仓库:https://github.com/timerring/front-end-tutorial 】或者公众号【AIShareLab】回复 javascript 也可获取。 文章目录 数组的基本使用定义数组和数组单元访问数组和数组索引数据单元值类型数组长度属性操作数组 数组:(…...
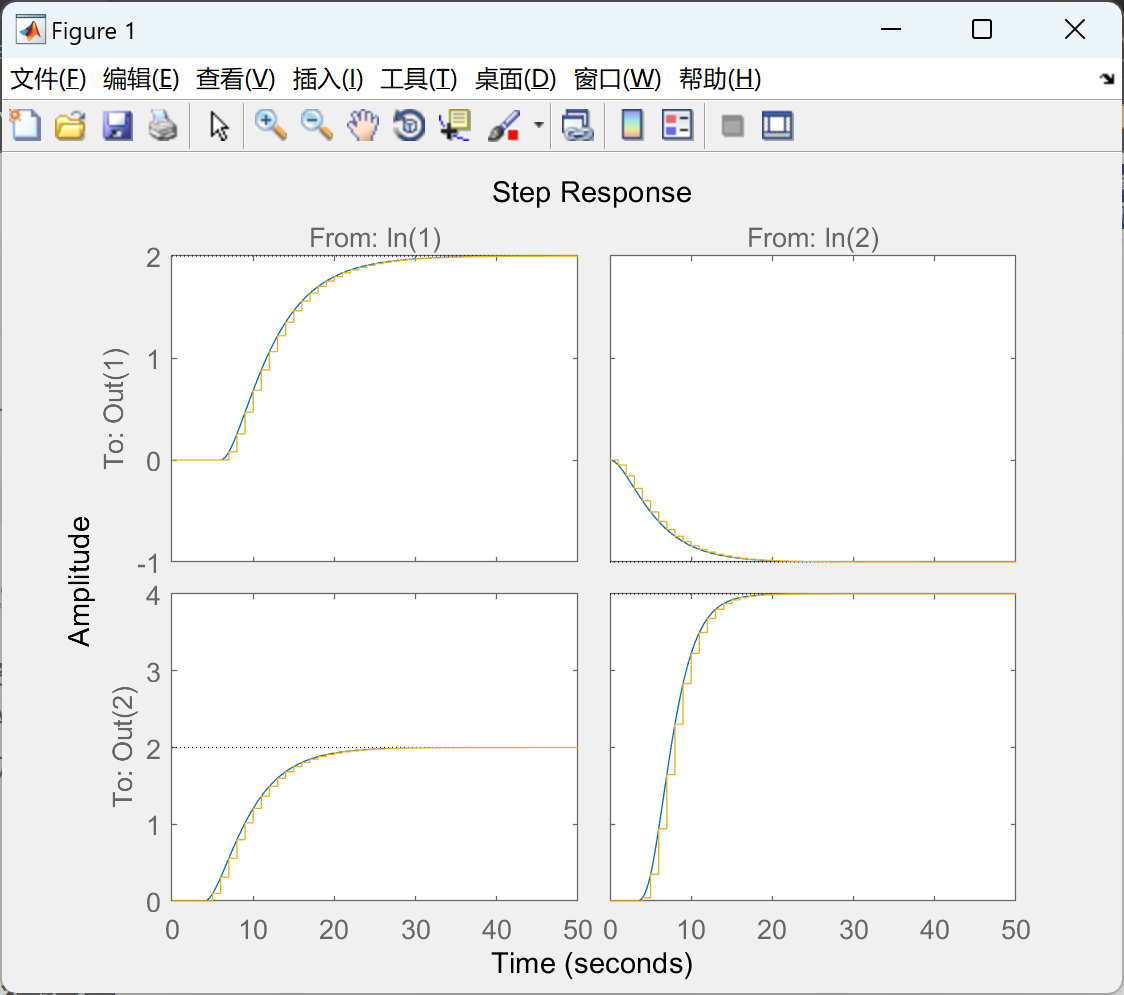
【模型预测控制MPC】使用离散、连续、线性或非线性模型对预测控制进行建模(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Golang之路---01 Golang VS Code创建项目
Golang VS Code创建项目 代码组织 Golang使用包和模块来组织代码,包对应到文件系统就是文件夹,模块就是xxx.go的go源文件。一个包中会有多个模块,或者多个子包。 早期使用的是gopath来管理项目,不方便,比较麻烦&…...

vue 表单form-item模板(编辑,查看,新建)
目录 formatFormData 后端数据格式编辑 JSON解析和生成 加载(请求前,await后) formComp formatFormData 后端数据格式 为空的,可以直接不提交/提交null/undefined JSON解析和生成 var str {"name": "…...

【IC设计】DC工具的target、link、synthetic、symbol库
Specifying Libraries You use dc_shell variables to specify the libraries used by Design Compiler. Table 4-1 lists the variables for each library type as well as the typical file extension for the library. 你使用dc_shell变量去指定dc要使用的库。下表列出了每种…...

redisson常用APi-Example
中文文档目录 redisson中文文档目录 分布式对象 package com.example.redissondemo.test;import com.example.redissondemo.RedissonDemoApplication; import com.example.redissondemo.test.domain.Order; import lombok.Data; import lombok.extern.slf4j.Slf4j; import o…...

小程序学习(四):WXML模板语法
WXML模板语法-数据绑定 1.数据绑定的基本原则 ①在data中定义数据 ②在WXML中使用数据 2.动态绑定属性 WXML模板语法-事件绑定 3.什么是事件 4.小程序中常用的事件 5.事件对象的属性列表 6.target和currentTarget的区别 7.bindtap的语法格式 8.在事件处理函数中为data中的数据…...

IDEA好用的插件总结
IdeaVim 这个看个人喜好,我比较喜欢用vim,并且支持自定义修改按键绑定alibaba java code guidelines alibaba的java编程规范plantUML 绘制UML,支持语言显示plantUML integration 能够直接将代码转化为UML图,非常方便rainbow brack…...

如何在Linux系统中安装ActiveMQ
1、环境 ActiveMQ是一个纯Java程序,这里安装5.18.2版ActiveMQ,该版MQ运行在JDK 11环境内,为此需要先搭建JDK 11环境,这里安装JDK 15。 1.1、卸载 卸载开源JDK软件包,如下所示: [rootlocalhost ~]# rpm -…...

【Latex】常用公式编辑与符号:公式换行,标号居中、常用符号等
【Latex】常用公式编辑与符号 文章目录 【Latex】常用公式编辑与符号1. 公式换行,且标号居中2. 常用符号3. 常用的希腊字母 1. 公式换行,且标号居中 \begin{equation}\label{eq14} \begin{aligned}a & b/c, \\d & e/f \end{aligned} \end{equ…...
【ArcGIS Pro二次开发】(55):给多个要素或表批量添加字段
在工作中可能会遇到这样的场景:有多个GDB要素、表格,或者是SHP文件,需要给这个要素或表添加相同的多个字段。 在这种情况下,手动添加就变得很繁琐,于是就做了这个工具。 需求具体如下图: 左图是待处理数据…...
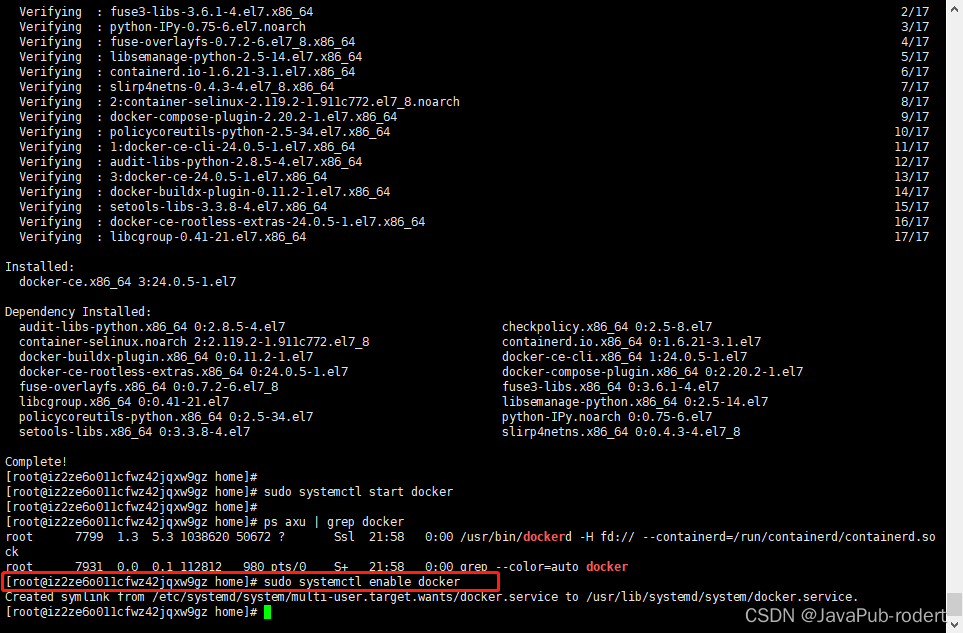
CentOS7.3 安装 docker
亲测、截图 阿里云服务器 文章目录 更新源2345 启动开机自启 更新源 sudo yum update -y2 sudo yum install -y yum-utils device-mapper-persistent-data lvm23 sudo yum-config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo4 sudo yum …...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
