[模版总结] - 集合划分类DFS模版
题目描述
给定一个数组,给定一个数字k, 问能不能讲数组内数等分成k份,使得每一个集合中数和相等。
题目链接
下面两道题问题及其类似,可作为同一类题目思考
Leetcode 698
Leetcode 473
题目思路
这道题是一道经典集合划分类问题,这类问题问询通常是判读是否将一个集合里面的所有元素划分到不同满足一定条件的子集合中。
集合划分也是思路和排列组合类似,可以想象成给球分桶的问题,这种类型的题目通常有两个思考方式:给每一个球选桶,给每一个桶选球
1. 给每一个球选桶:我们每一层递归的是球,每一个球每层递归可以选择进入一个桶,以此类推。
2. 给每一个桶选球:我们每一层递归的是桶,相当于每一层给某一个桶塞球,当塞满了就开始进入下一个桶。
这里的球就是指集合中的每一个数,而桶则是指等分的每一个子集合。
1. 暴力DFS
给每一个数选择一个子集合(超时)- 思路很简单,每一层递归是给当前数字选择一个子集合,如果当前子集合超过等分值那么跳过,直到所有数字选完子集合后,比较子集合中是否相等即可。
代码如下:
class Solution {int[] arr;int avg;public boolean canPartitionKSubsets(int[] nums, int k) {int sum = 0;for (int i: nums) sum+=i;avg = sum/k;if (avg*k!=sum) return false;arr = nums;return dfs(0, new int[k]);}private boolean dfs(int idx, int[] bkts) {if (idx==arr.length) {// 所有球找完桶,这时确定每个桶里面的数字for (int i: bkts) {if (i!=avg) return false;}return true;}// 开始选桶for (int i=0; i<bkts.length; i++) {if (bkts[i]+arr[idx] > avg) continue;// 桶里还能加bkts[i]+=arr[idx];if (dfs(idx+1, bkts)) return true;bkts[i]-=arr[idx]; // 组合类题目要回溯}return false;}
}时间复杂度:, 每一个数字有k个选择方式;空间复杂度:
,如果忽略递归占用的额外占空间。
给每一个子集合加入数(通过) - 相当于给每一个子集合选择一套数字,如果这个子集合塞满了,则继续下一个子集合直到所有的“桶”都塞完了“球”。思路和球选桶类似,但是需要开额外空间加入标记位来确认当前球被选过没有。
代码如下:
class Solution {int[] arr;int avg;public boolean canPartitionKSubsets(int[] nums, int k) {int sum = 0;for (int i: nums) sum+=i;avg = sum/k;if (avg*k!=sum) return false;arr = nums;return dfs(0, 0, new int[k], new boolean[nums.length]);}private boolean dfs(int idx, int bkt, int[] bkts, boolean[] visited) {if (bkt==bkts.length) {for (int i: bkts) {if (i!=avg) return false;}return true;}if (bkts[bkt]==avg) {// 目前选满了,换下一个桶return dfs(0, bkt+1, bkts, visited);}// 当前桶塞球for (int i=idx; i<arr.length; i++) {if (visited[i]) continue; //球用过了if (bkts[bkt]+arr[i]>avg) continue;// 当前桶可以塞visited[i] = true;bkts[bkt]+=arr[i];if (dfs(i+1, bkt, bkts, visited)) return true;visited[i] = false;bkts[bkt]-=arr[i]; // 组合问题回溯}return false;}
}时间复杂度:, 比球选桶的思路快了不少, 每一个桶在选球时有
个选法;空间复杂度:
,需要开额外空间进行去重。
2. DFS + 剪枝优化
给每一个数选择一个子集合(通过) - 不难理解,在递归寻找解的过程中,有很多重复解的情况,比如桶1选择2,3,4号球,桶2选择5,6号球,这种情况和桶1选择5,6号球,桶2选择2,3,4号球是重复情况。我们只是需要知道组合数而不需要知道排序。
代码如下:
class Solution {int[] arr;int avg;public boolean canPartitionKSubsets(int[] nums, int k) {int sum = 0;for (int i: nums) sum+=i;avg = sum/k;if (avg*k!=sum) return false;arr = nums;return dfs(0, new int[k]);}private boolean dfs(int idx, int[] bkts) {if (idx==arr.length) {// 所有球找完桶,这时确定每个桶里面的数字for (int i: bkts) {if (i!=avg) return false;}return true;}// 开始选桶for (int i=0; i<bkts.length; i++) {if (bkts[i]+arr[idx] > avg) continue;// 相邻两个桶值相同,那么选了上一个就不需要选这个if (i>0 && bkts[i-1]==bkts[i]) continue;// 桶里还能加bkts[i]+=arr[idx];if (dfs(idx+1, bkts)) return true;bkts[i]-=arr[idx]; // 组合类题目要回溯}return false;}
}时间复杂度:最坏, 具体复杂度很难估计;空间复杂度:
,如果忽略递归占用的额外占空间。
给每一个子集合加入数(通过) - 给桶塞球的思路我们可能会给两个桶塞入相同组合的球,那么可以设置一个HashMap记录之前的球选择,如果球组合被选过那么直接返回结果而不在往后计算。
注:这里还有一个优化是对boolean[] visited数组进行空间优化,我们可以直接用一个N位 int 来保存访问信息,但你需要熟悉下面几个位操作 - 非常巧妙
1. ((int >> i) & 1) == 1: 判断第i个球是否用过 等价于 visited[i]==true
2. int |= 1<<i: 给第i个球标记为访问 等价于 visited[i] = true
3. int ^= 1<<i: 给第i个球回溯为未访问 等价于 visited[i] = false
代码如下:
class Solution {int[] arr;int limit;HashMap<Integer, Boolean> paths = new HashMap<>();public boolean canPartitionKSubsets(int[] nums, int k) {int sum = 0;for (int i: nums) sum+=i;boolean[] visited = new boolean[nums.length];int avg = sum/k;if (avg*k!=sum) return false;arr = nums;limit = avg;// 骚套路剪枝通过int来记录每一个元素使用与否int used = 0;return dfs(used, 0, new int[k], 0);}private boolean dfs(int used, int bkt, int[] bkts, int start) {// 以k个桶的角度选择候选if (bkt==bkts.length) return true;if (bkts[bkt]==limit) {boolean res = dfs(used, bkt+1, bkts, 0);paths.put(used, res);return res;} if (paths.containsKey(used)) {return paths.get(used);}for (int i=start; i<arr.length; i++) {if (((used>>i) & 1)==1) continue;if (bkts[bkt]+arr[i]>limit) continue;used |= 1 << i;bkts[bkt]+=arr[i];if (dfs(used, bkt, bkts, start+1)) return true;bkts[bkt]-=arr[i];used ^= 1 << i;}return false;}
}时间复杂度:最坏, 比球选桶的思路快了不少, 每一个桶在选球时有
个选法;空间复杂度:
,虽然省去了visited的空间,但是需要开额外空间进行路径去重。
相关文章:
[模版总结] - 集合划分类DFS模版
题目描述 给定一个数组,给定一个数字k, 问能不能讲数组内数等分成k份,使得每一个集合中数和相等。 题目链接 下面两道题问题及其类似,可作为同一类题目思考 Leetcode 698 Leetcode 473 题目思路 这道题是一道经典集合划分类问题&#…...

JavaScript中复制新的数组与原数组删除某个值——不影响新复制的数组的方法详解
系列文章目录 文章目录 系列文章目录前言一、使用slice()方法复制数组二、使用concat()方法复制数组三、使用扩展运算符(...)复制数组总结 前言 在JavaScript中,我们经常需要处理数组的复制和修改。本文将详细介绍如何在JavaScript中复制一个新的数组,并…...
easyui主表子表维护页面
easyui主表子表维护页面 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><title>Title</title><!-- <#include "common.html"/> --><link rel"stylesheet" type&quo…...

k8s exam
Pause 容器是 Pod 中的第一个启动的容器,其他所有的用户容器都是其子进程当 Pod 被从节点中删除时,与之关联的 emptyDir 中的数据也将被永久删除。持久存储用PV,PVCService 资源定义了如何访问应用,但实际的网络流量管理和路由是由…...

C#,中国福利彩票《刮刮乐》的数学算法(02)——时来运转
1 中国福利彩票 中国福利彩票始于1987年7月27日,以“团结各界热心社会福利事业的人士,发扬社会主义人道主义精神,筹集社会福利资金,兴办残疾人、老年人、孤儿福利事业和帮助有困难的人”、即“扶老、助残、救孤、济困”为宗旨。随…...

我的观影记录表【个人向】
目录 前言电影评分标准闪电侠(2023)银河护卫队3(2023) 前言 这里是我本人的观影记录,这个想法2年前就有了,但是一直比较懒,现在(上班摸鱼)准备重新开始,评价…...
网络安全策略应包含哪些?
网络安全策略是保护组织免受网络威胁的关键措施。良好的网络安全策略可以确保数据和系统的保密性、完整性和可用性。以下是一个典型的网络安全策略应包含的几个重要方面: 1. 强化密码策略:采用强密码,要求定期更换密码,并使用多因…...
【Git】Git GitHub
1. Git1.1 Git基本操作1.2 Git版本回退1.3 Git分支操作 2. Git 配合GitHub2.1 生成密钥2.2 GitHub添加公钥2.3 Git连接GitHub2.4 本地仓库关联远程仓库2.5 本地代码push远程仓库2.6 本地clone远程仓库2.7 本地fetch和pull 1. Git 1.1 Git基本操作 touch test.py 工作区创建文…...
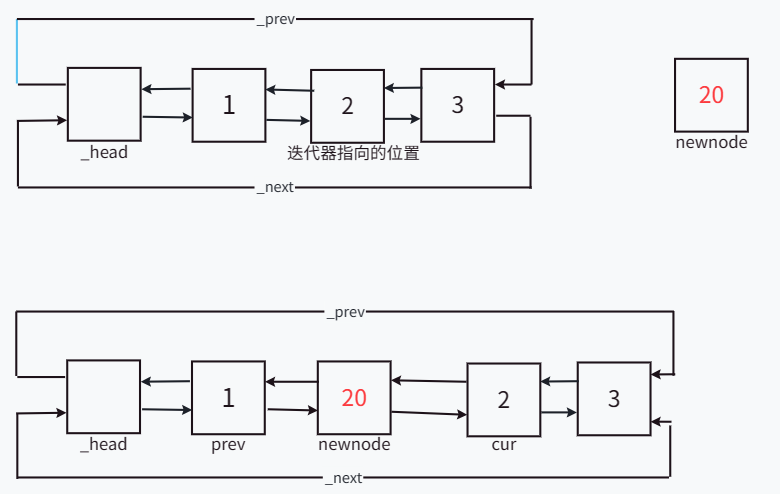
[STL]详解list模拟实现
[STL]list模拟实现 文章目录 [STL]list模拟实现1. 整体结构总览2. 成员变量解析3. 默认成员函数构造函数1迭代器区间构造函数拷贝构造函数赋值运算符重载析构函数 4. 迭代器及相关函数迭代器整体结构总览迭代器的模拟实现begin函数和end函数begin函数和end函数const版本 5. 数据…...

C和C++的区别与联系
C语言(C)和C语言(C)是两种编程语言,它们之间有许多区别和联系。以下是它们之间的主要区别和联系: 区别: 历史和起源: C语言是由Dennis Ritchie于20世纪70年代初在贝尔实验室开发的。…...

springboot通过接口执行本地shell脚本
首先创建springboot项目 shell脚本 #!/bin/shecho Hello World!然后编写执行shell脚本的util类 import java.io.BufferedInputStream; import java.io.BufferedReader; import java.io.InputStreamReader; import java.util.ArrayList; import java.util.List;pub…...

工欲善其事必先利其器,IT工作电脑更要维护好
目录 一:电脑的组成 二:维护措施 三:助力记忆 一:电脑的组成 当谈到电脑主机时,我们通常指的是电脑的中央处理器(CPU)、内存、主板、电源、硬盘、显卡、声卡、网卡等核心部件组成的整体。这些部件共同协作ÿ…...
移动端个人中心UI设计
效果图 源码如下 页面设计 <template><div class"container"><!-- 顶部用户信息 start--><div class"header"><div class"user-info"><van-image class"user-img" round width"70" :sr…...

开发接口,你需要先搞懂这些概念!
SOA Service Oriented Ambiguity 即面向服务架构, 简称SOA。 SOA的提出是在企业计算领域,就是要将紧耦合的系统,划分为面向业务的,粗粒度,松耦合,无状态的服务。服务发布出来供其他服务调用,一…...

zookeeper常用命令
zkClient 简介 zkClient是简易的客户端程序 进入zkClient 在bin目录下输入zkCli.sh 节点命令 增 create 路径 数据 -s:顺序节点 -e:临时节点 默认情况下,不添加-s或者-e参数的,创建的是持久节点改 set 路径 数据 版本…...

亚马逊水基灭火器UL8测试报告ISO17025实验室办理
在跨境电商平台上销售的境外电商,在美国市场中需要提供相关的安全规范报告。其中,美国相关部门要求,如果商家未能提交UL(Underwriters Laboratories)标准的检测报告,将会被责令停止销售。而为了在亚马逊、T…...

Shell学习脚本-if多分支结构
语法: if 条件then指令集 else指令集 fi特殊写法: if [ -f "$file1" ]; then echo 1; else echo 0; fi 相当于: [ -f "$file1" ] && echo 1 || echo 0 多分支结构: if 条件then指令 elif 条件th…...

[SQL挖掘机] - 窗口函数 - lead
介绍: lead() 是一种常用的窗口函数,它用于获取某一行之后的行的值。它可以用来在结果集中的当前行后面访问指定列的值。 用法: lead() 函数的语法如下: lead(列名, 偏移量, 默认值) over (partition by 列名1, 列名2, ... order by 列名 [asc|desc]…...

PyTorch Lightning教程四:超参数的使用
如果需要和命令行接口进行交互,可以使用Python中的argparse包,快捷方便,对于Lightning而言,可以利用它,在命令行窗口中,直接配置超参数等操作,但也可以使用LightningCLI的方法,更加轻…...
2023 蓝桥杯真题B组 C/C++
https://www.dotcpp.com/oj/train/1089/ 题目 3150: 蓝桥杯2023年第十四届省赛真题-冶炼金属 题目描述 小蓝有一个神奇的炉子用于将普通金属 O 冶炼成为一种特殊金属 X。这个炉子有一个称作转换率的属性 V,V 是一个正整数,这意味着消耗 V 个普通金 属 O…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
