GoogleLeNet Inception V2 V3
文章目录
- 卷积核分解
- 第一步分解,对称分解
- 第二步分解,非对称分解
- 在Inception中的改造
- 一般模型的参数节省量
- 可能导致的问题
- 针对两个辅助分类起的改造
- 特征图尺寸缩减
- Model Regularization via Label Smoothing——LSR
- 问题描述,也就是LSR解决什么问题
- 解决办法
- 网络结构
- Inception V2 & Inception V3
前一篇的Batch Normalization只是Inception V2,V3的一个前菜。真正提出Inception V2,V3的概念的是在论文Rethinking the Inception Architecture for Computer Vision中,这篇论文中综合了Batch Normalization的概念,然后提出了自己的一些改进。通过不同的组合,形成了Inception V2,V3的概念。
我们这一篇就记录了一下这篇论文提出了改进,然后记录一下什么是V2,V3与V2相比又改了点什么东西。
这篇论文主要的论点是围绕着降低计算开销和内存开销来展开的,因为是要为移动设备做准备。
卷积核分解
第一步分解,对称分解
对称分解是相对于下一步的非对称分解而言的,就是将一个n * n的卷积核分解成若干个m * m的卷积核, m < n。
论文中的标题是Factorizing Convolutions with Large Filter Size。或者简单的说就是把一个大的卷积核分解成几个小的卷积核。
这样做的好处是总体参数减少了,自然训练和推理的开销都会减少。
文中举的例子是一个5 * 5的卷积核可以分解成两个3 * 3的卷积核。
如图:

那么,参数的个数就从 5 * 5 = 25 缩减到 2 * 3 * 3 = 18。
第二步分解,非对称分解
上一步的小卷积核都是正方形的,这次使用的逻辑是将一个n * n的卷积核分解成一个1 * n的卷积核和一个 n * 1的卷积核。
如图:
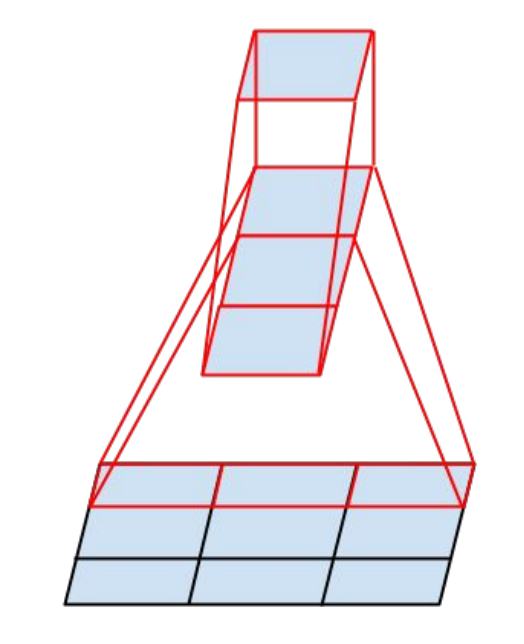
在Inception中的改造
原始的Inception结构:
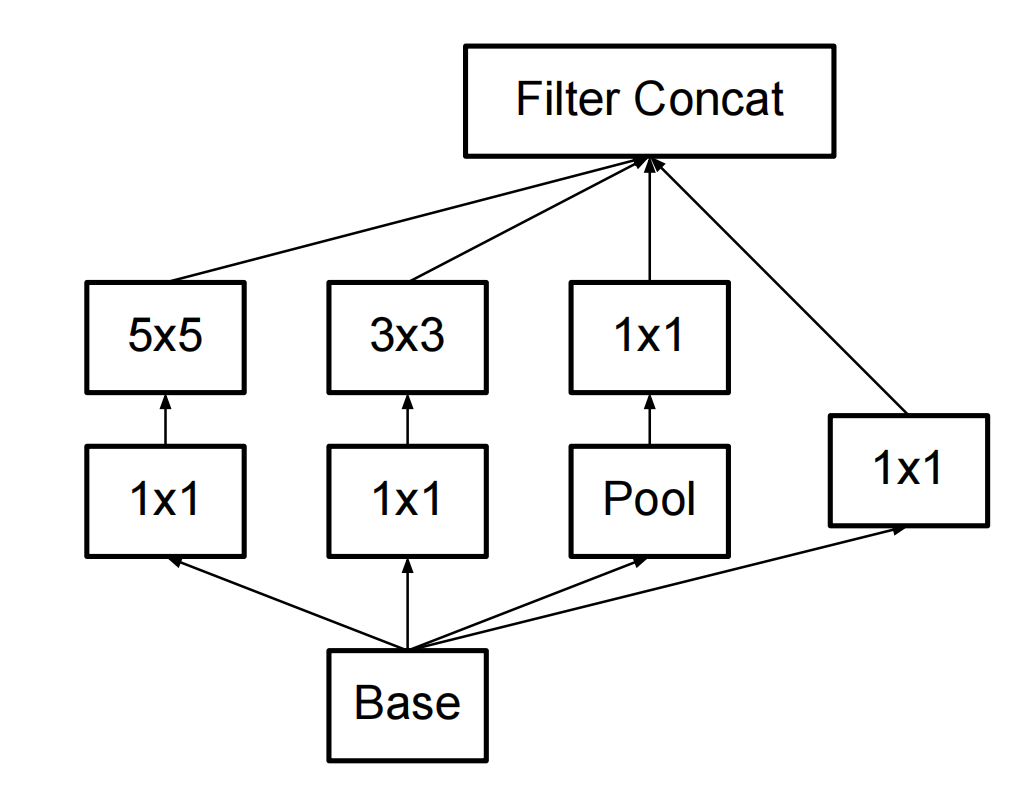
经过第一步改造为:
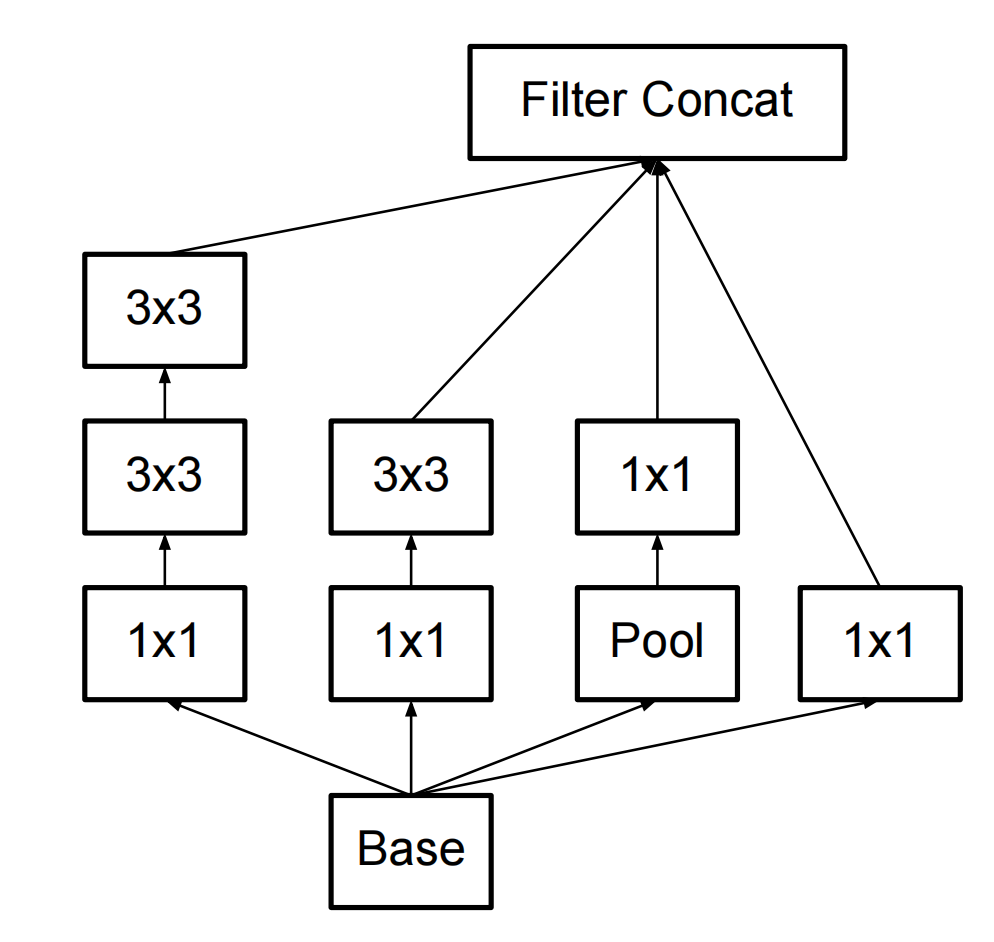
再经过第二步改造为:
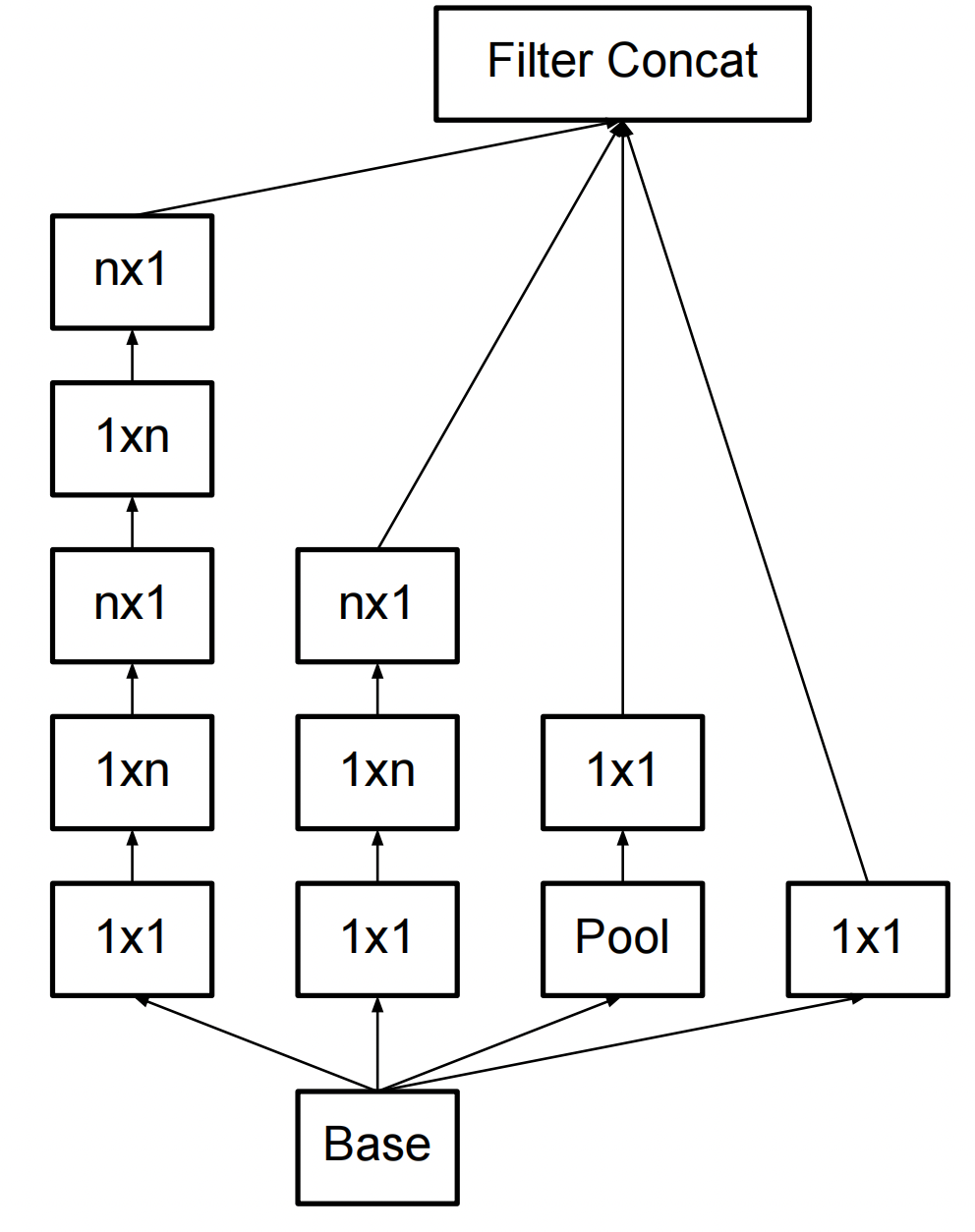
如果是上面的3的话,这里的n就等于3。当然在整个GoogleLeNet中,这个n不一定是等于3。
一般模型的参数节省量
所以在文章中,对一般的网络做这个改造的参数节省量做了一个评估。
一般在CNN网络中,featrue map都是越来越是高层特征,所以尺寸是缩小的,在论文中提出了公式:
n = α m n=\alpha m n=αm
- n应该是前一层的输出尺寸(相对于卷积层,或者一个Inception单位)
- m为后一层的输入尺寸(同上)
所以一个改造前的卷积层的参数数量为:
m ∗ w ∗ w ∗ n = w 2 ∗ m ∗ α m = α w 2 m 2 m * w * w * n = w^2 * m * \alpha m = \alpha w^2 m^2 m∗w∗w∗n=w2∗m∗αm=αw2m2,w为卷积核的尺寸。
如果把这个 w ∗ w w * w w∗w的拆成了两个卷积核,那么前一层的输出和后一层的输入的尺寸相同,在数学上这个原来的端到端参数 α \alpha α在每一层中可以计算为 α \sqrt{\alpha} α
所以计算的公式就变成为:
w ∗ w ∗ α m ∗ α + w ∗ w ∗ α ∗ m w * w * \alpha m * \sqrt{\alpha} + w * w * \sqrt{\alpha} * m w∗w∗αm∗α+w∗w∗α∗m
简化后:
w 2 α ( α + 1 ) m 2 w^2\sqrt{\alpha}(\alpha+1)m^2 w2α(α+1)m2
如果尺寸不变,也就是 α = 1 \alpha = 1 α=1的时候,前一层是5,后一层是3的情况下,节省的参数量就是28%。
可能导致的问题
- 是否会减少模型的表达能力(Does this replacement result in any loss of expressiveness)
- 还有个问题就是第一层卷积后面,比如第一个3 * 3后面跟什么激活函数,是线性的Sigmond还是非线性的ReLU(If our main goal is to factorize the linear part of the computation, would it not suggest to keep linear activations in the first layer?)
论文中做了一些实验,得到的结果为:
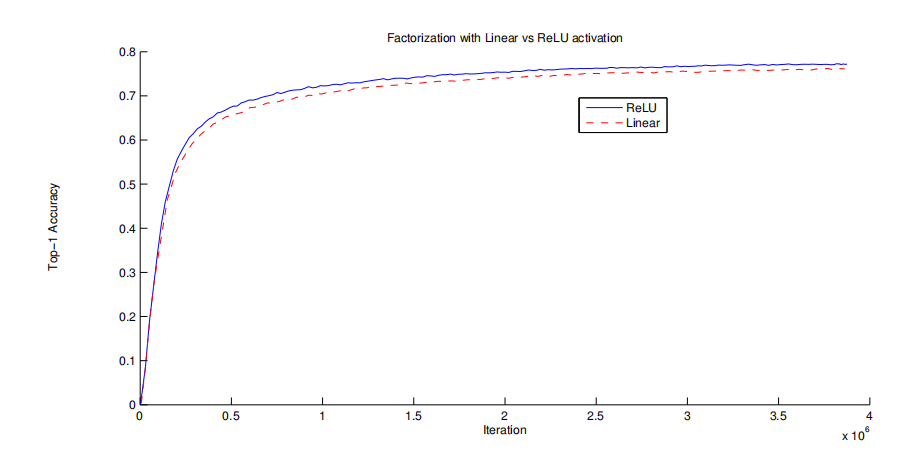
结果是使用ReLU要好一些,而且可以配合Batch Normalization一起使用。
针对两个辅助分类起的改造
论文中提到,虽然说在v1中设计了两个辅助分类器,两个辅助分类起位于网络的较前的层,在训练过程中可以更有效的利用梯度(前一篇提到了https://blog.csdn.net/pcgamer/article/details/131914842?spm=1001.2014.3001.5502)。
但是这篇文章是认为,这两个分类起没毛用。具体是为啥没说,估计是用数据做了验证吧,原话是:
Interestingly, we found that
auxiliary classifiers did not result in improved convergence early in the training: the training progression of network with and without side head looks virtually identical before both models reach high accuracy。Near the end of training, the network with the auxiliary branches starts to overtake the accuracy of the network without any auxiliary branch and reaches a slightly higher plateau.
Also used two side-heads at different stages in the
network. The removal of the lower auxiliary branch did not have any adverse effect on the final quality of the network。
这篇论文中提到,在训练过程的前期,这两个分类器没有起到什么作用,只是在快结束的时候可以提升一点准确率
另外提到的是,如果在这两个分类器前面增加一个 batch-normalization层或者dropout层更有用。
在后面提到的v2网络中的BN网络就是增加了这个Batch Normalization层。
特征图尺寸缩减
论文中的标题是Efficient Grid Size Reduction。这块简单解释下,论文中在这一小节中的描述是:Traditionally, convolutional networks used some pooling operation to decrease the grid size of the feature maps. In order to avoid a representational bottleneck, before applying maximum or average pooling the activation dimension of the network filters is expanded。
这一小段描述的是,在一般的CNN网络中,为了不损失特征,保持网络的表达能力,但是又要不断通过更小尺寸的卷积核一步一步提取高维特征,一般在卷积完之后,filter的宽度会变宽。观察一般的CNN网络,从input层开始,卷积一层之后,featrue map尺寸变小,但是channels变多,我的理解是高维特征尺寸小,但是为了不损失,需要多提取一些高维特征,也就是较多的通道数(channels)
一般的网络中,下一层featrue map的尺寸是上一层的一半(宽高都是),然后通道数翻倍。也就是文中的: starting a
d × d d×d d×d grid with k filters, if we would like to arrive at a d 2 × d 2 d2 × d2 d2×d2 grid with 2k filters, we first need to compute a stride-1 convolution with 2k filters and then apply an additional pooling step。
那么操作次数是 2 d 2 k 2 2d^2k^2 2d2k2。
一般来说,是在卷积之后跟一个pooling层。那么最简单的简化方法就是把这两个层换一下,因为pooling之后,grid或者说featrue map的尺寸就只有原来的四分之一了。
那么操作数就变成了 2 ( d 2 ) 2 k 2 2 (\frac{d}{2})^2k^2 2(2d)2k2了。
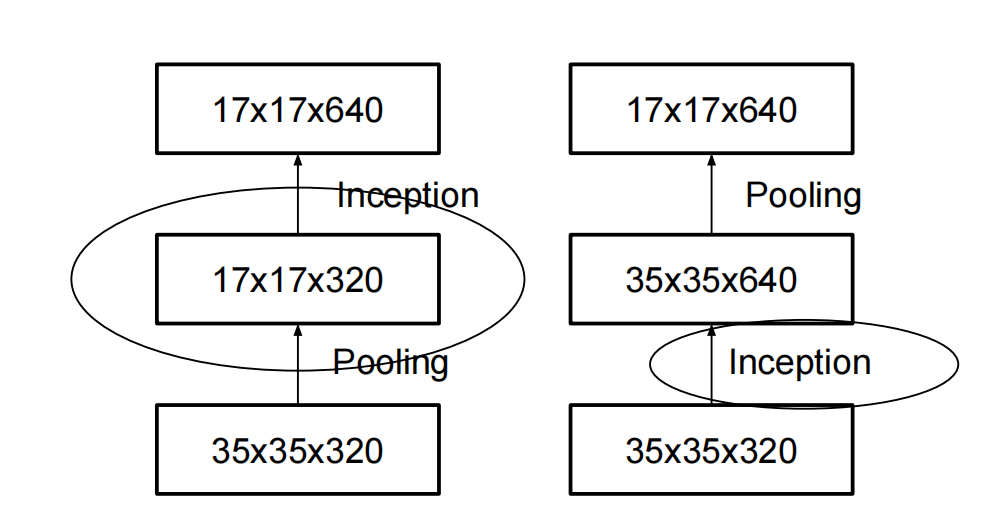
(尺度的宽高减半,层数翻倍)
但是这有一个重要的问题是,池化层会有很多的损失,造成网络的表达能力下降,文中称作representational bottlenecks。
所以文中提出了另外一种结构:
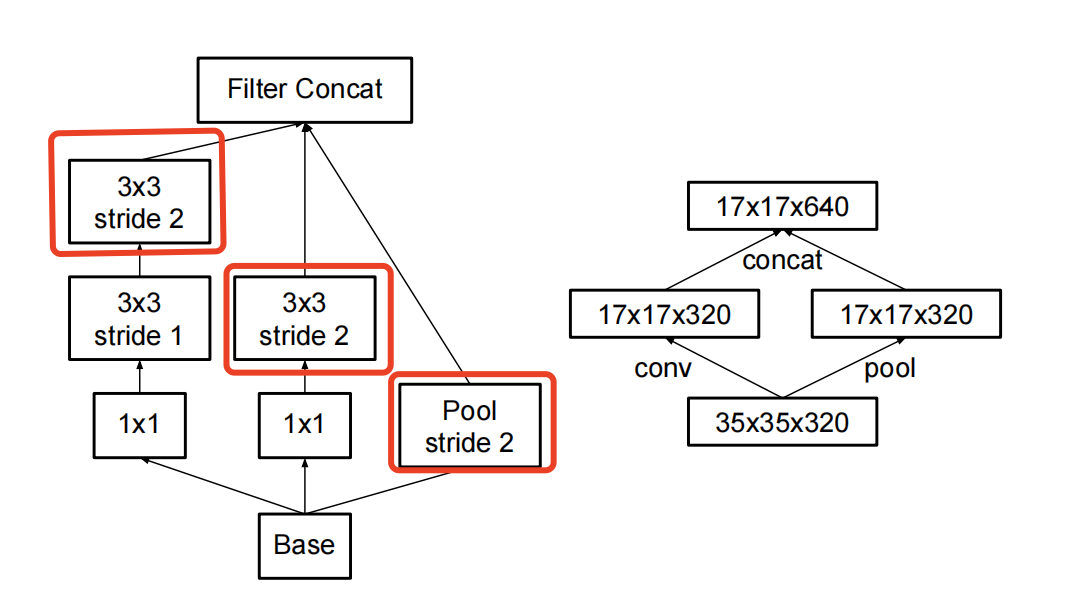
文中的描述为:We can use two parallel stride 2
blocks: P and C. P is a pooling layer (either average or maximum pooling) the activation, both of them are stride 2 the filter banks。
简单来说,就是把卷积操作中的stride = 1变成了 stride = 2。这样会减少不少的计算量,步长大了嘛。
Model Regularization via Label Smoothing——LSR
问题描述,也就是LSR解决什么问题
这个改进就是基于交叉熵的损失函数上做的一个改造:
基于交叉熵的损失函数是(之前的文章描述过
https://blog.csdn.net/pcgamer/article/details/131713549?spm=1001.2014.3001.5501):
不过之前的文章中的p和q与论文中的恰好是反过来的,这里以论文为准。
H ( p , q ) = − ∑ k = 1 K l o g ( p ( x ) ) q ( x ) H(p,q) = -\sum_{k=1}^K{log(p(x))q(x)} H(p,q)=−k=1∑Klog(p(x))q(x)
然后在论文里,把 q ( x ) q(x) q(x)这个标签的数据分布描述成一个狄拉克分布,也就是一个激活函数,因为在K个列表中只有一个1,记做 δ k , y \delta{k,y} δk,y,后续 q ( x ) q(x) q(x)就用 δ k , y \delta_{k,y} δk,y代替。
这里存在一个问题是,在计算交叉熵和反向传播的时候,网络根据损失函数,会去拟合label的分布 q ( x ) q(x) q(x)。
比如一个三分类,标签数据是(0, 1, 0),而预测出来的结果是(0.4, 0.5, 0.1)。
那么此时的损失函数计算为:
l = − ( 0 ∗ l o g ( 0.4 ) + 1 ∗ l o g ( 0.5 ) + 0 ∗ l o g ( 0.1 ) ) ≈ 0.3 l=-(0 * log(0.4) + 1 * log(0.5) + 0 * log(0.1)) \approx 0.3 l=−(0∗log(0.4)+1∗log(0.5)+0∗log(0.1))≈0.3
而如果预测结果是(0.1, 0.8, 0.1)的话,损失值为:
l = − ( 0 ∗ l o g ( 0.1 ) + 1 ∗ l o g ( 0.8 ) + 0 ∗ l o g ( 0.1 ) ) ≈ 0.1 l=-(0 * log(0.1) + 1 * log(0.8) + 0 * log(0.1)) \approx 0.1 l=−(0∗log(0.1)+1∗log(0.8)+0∗log(0.1))≈0.1
也就是越接近,损失越小(好像是废话,网络不就是要干这个么)。其实就是要提出一个过拟合的方法,论文中的描述是:
the model becomes too confident about its predictions。模型对预测过于自信。。。。
解决办法
论文中提出的解决办法就是增加一个超参数 ϵ \epsilon ϵ,然后再引入另外一个随机变量分布 u u u,这个 ϵ \epsilon ϵ就用于分配两个分布的权重。
也就是把上面计算损失函数的 q ( x ) q(x) q(x)用 q ′ ( x ) q^{'}(x) q′(x)来代替:
q ′ ( x ) = ( 1 − ϵ ) δ k , y + ϵ u ( k ) q^{'}(x)=(1-\epsilon)\delta_{k,y} + \epsilon u(k) q′(x)=(1−ϵ)δk,y+ϵu(k)
让label的分布从一个纯粹的 δ k , y \delta_{k,y} δk,y分布变一点点,这个引入的分布通常是一个平均分布,也就是 u ( k ) = 1 K u(k) = \frac{1}{K} u(k)=K1。上式就变成:
q ′ ( x ) = ( 1 − ϵ ) δ k , y + ϵ K q^{'}(x)=(1-\epsilon)\delta_{k,y} + \frac{\epsilon}{K} q′(x)=(1−ϵ)δk,y+Kϵ
然后损失函数就变成:
H ( q ′ , p ) = − ∑ k = 1 K l o g p ( k ) q ′ ( k ) = ( 1 − ϵ ) H ( q , p ) + ϵ H ( u , p ) H(q^{'}, p)=-\sum_{k=1}^Klogp(k)q^{'}(k)=(1-\epsilon )H(q, p) + \epsilon H(u,p) H(q′,p)=−k=1∑Klogp(k)q′(k)=(1−ϵ)H(q,p)+ϵH(u,p)
论文中的 K K K和 ϵ \epsilon ϵ取值为:In our ImageNet experiments with K = 1000 classes,
we used u(k) = 1/1000 and ϵ \epsilon ϵ = 0.1.
这个方法为准确度贡献了 0.2 0.2% 0.2。
另外,论文中提到的这个动作是logit这个位置,这个位置位于softmax激活层之前。
logit的概念(借用一下):
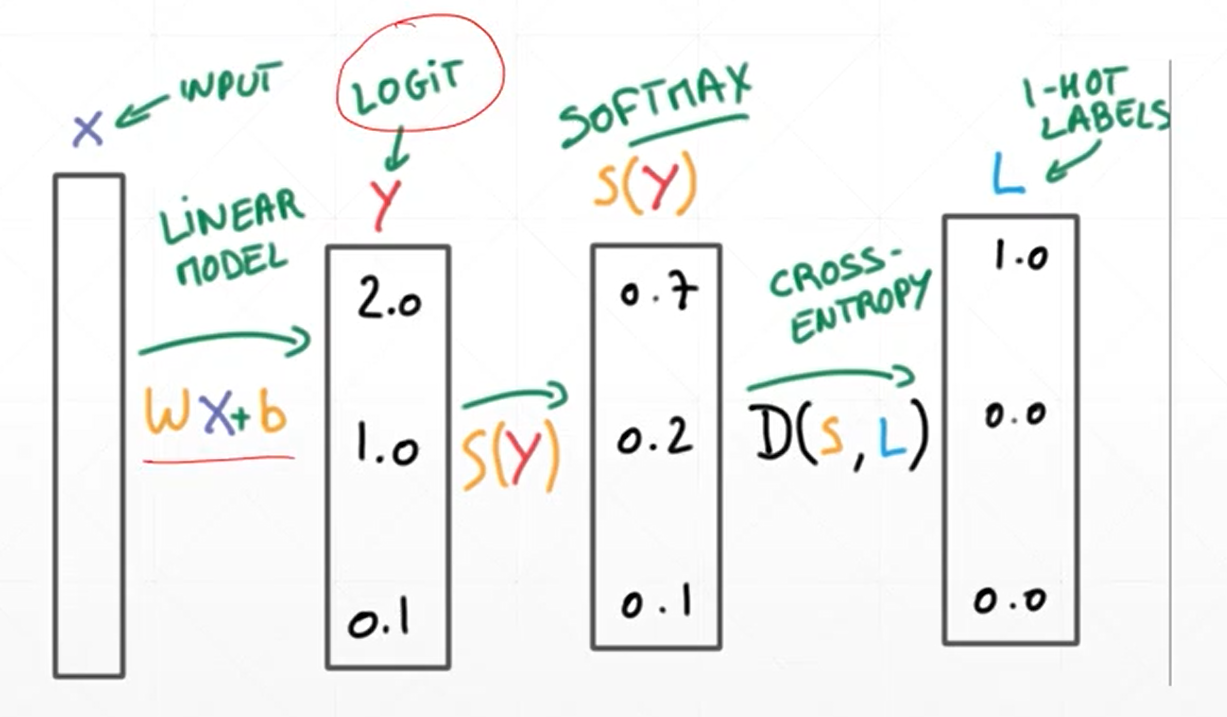
网络结构
V2的组成如下表:
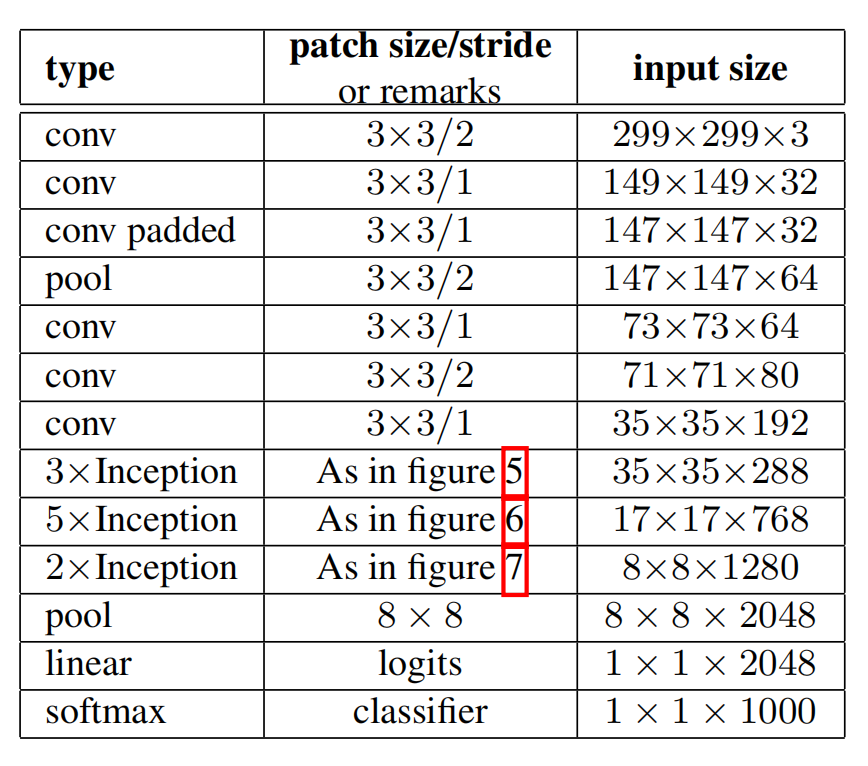
- V1中的最初的7 * 7的卷积层变成了3个 3 * 3的卷积层。
- 三个Inception部分
- 第一个部分采用的是图1-对称分解的方式组成的Inception模块,连续3个Inception模块。
- 第二部分采用的是图2-不对称分解组成的Inception模块,连续5个。在论文中关于这块描述是:In practice, we have found that employing this factorization does not work well on early layers, but it gives very good results on medium grid-sizes (On m×m feature maps, where m ranges between 12 and 20). On that level, very good results can be achieved by using 1 × 7 convolutions followed by 7 × 1 convolutions。
- 第三部分采用了一种新的方式:如图。
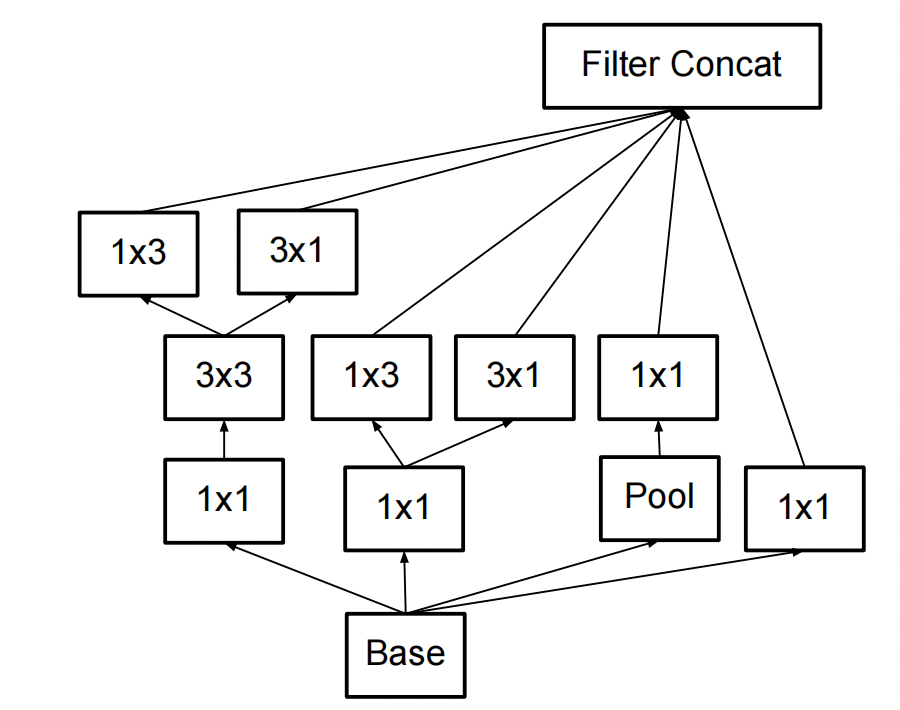
总共2个模块。
论文中对这种连接方式的描述是:This architecture is used on the coarsest (8 × 8) grids to promote high dimensional representations。We are using this solution only on the coarsest grid, since that is the place where producing high dimensional sparserepresentation is the most critical as the ratio of local processing
(by 1 × 1 convolutions) is increased compared to the spatial aggregation.。
讲的是这种构造只用于高层特征的featrue map中。也就是卷积了很多次的特征图中。在V2结构中,直接是用在网络的最后部分。
和图二相比,相当于就是把1 * n和n * 1的这两个动作由串行变成了并行,然后把并行卷积出来的featrue map进行连接,通道数相当于就翻倍了。应该是要利用不同尺寸的卷积进行不同尺寸特征的提取。
1 * 3和3 * 1卷积出来的尺寸不一样的问题,就通过在上一层的featrue map上做padding来补充(用的是0-padding的方法),来保证卷积出来的尺寸维持在8 * 8。
padding只针对宽的那个边进行,短的那边不需要填充。体现到代码上就是:
nn.Conv2d(8, 8, kernel_size=(1,3), padding=(0, 1))nn.Conv2d(8, 8, kernel_size=(3,1), padding=(1, 0))
另外,论文中提到了输入大小的问题,做了 299 * 299(stride=2+m-pooling) / 151 * 151(stride=1+m-pooling) / 79 * 79(stride=1)的比较,认为对于低分辨率的图像,还是使用相对较大的感受野(就是这个输入我理解就是要去裁剪或者缩放原图。),效果要更好,同样的逻辑也可以用到R-CNN的目标检测模型中。
Inception V2 & Inception V3
论文在Experiment章节中,把上述提出的改进点,一个一个加进去来测试结果,结论如图:
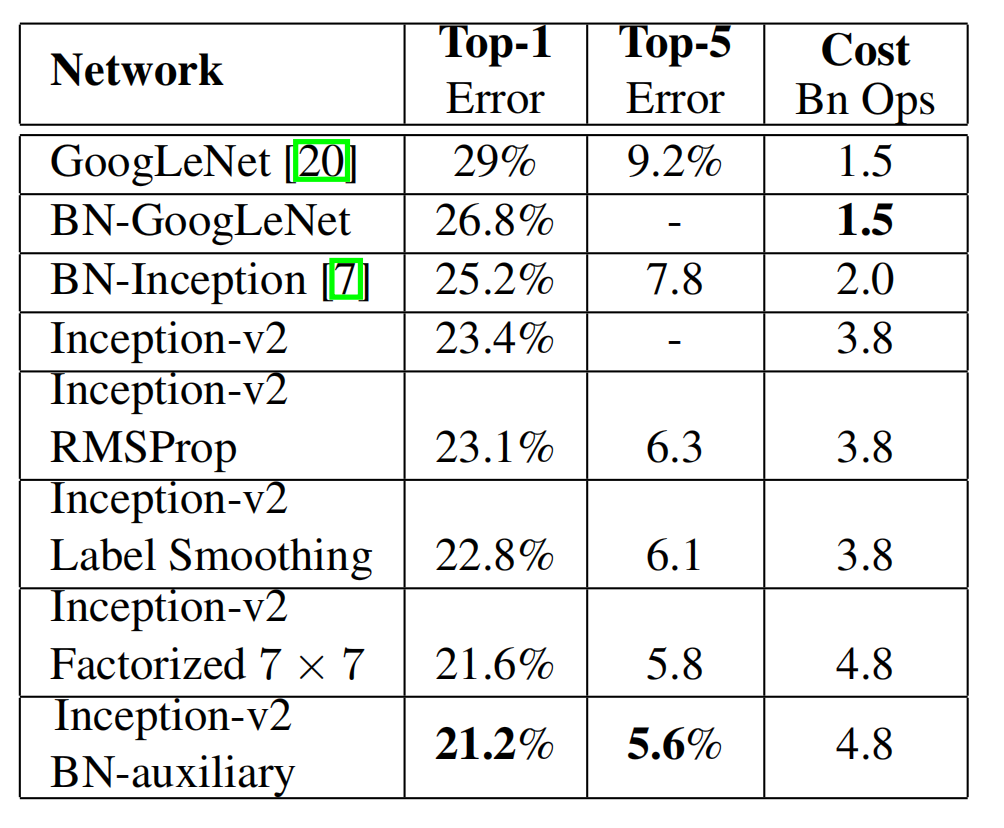
也就是说Inception v2是在v1的基础上(激活层前)上加了BN层。然后再慢慢加上LSR,加上7 * 7的分解,辅助分类器加上BN等操作。
最后一行就是Inception v3版本。
最后的V3版本效果最好。
相关文章:

GoogleLeNet Inception V2 V3
文章目录 卷积核分解第一步分解,对称分解第二步分解,非对称分解在Inception中的改造一般模型的参数节省量可能导致的问题 针对两个辅助分类起的改造特征图尺寸缩减Model Regularization via Label Smoothing——LSR问题描述,也就是LSR解决什么…...
【css】背景图片附着
属性:background-attachment 属性指定背景图像是应该滚动还是固定的(不会随页面的其余部分一起滚动)。 background-attachment: fixed:为固定; background-attachment: scroll为滚动 代码: <!DOCTYPE h…...
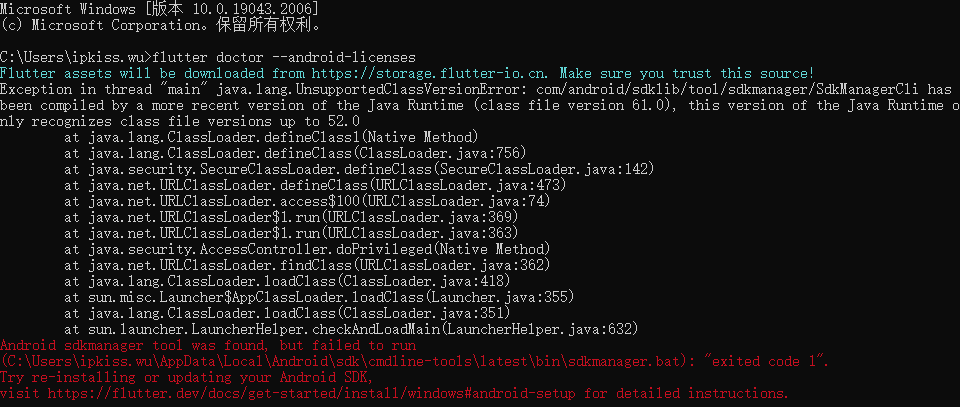
解决运行flutter doctor --android-licenses时报错
问题描述: 配置flutter环境时,会使用flutter doctor命令来检查运行flutter的相关依赖是否配好。能看到还差 Android license status unknown.未解决。 C:\Users\ipkiss.wu>flutter doctor Flutter assets will be downloaded from https://storage.…...

在使用Python爬虫时遇到503 Service Unavailable错误解决办法汇总
在进行Python爬虫的过程中,有时会遇到503 Service Unavailable错误,这意味着所请求的服务不可用,无法获取所需的数据。为了解决这个常见的问题,本文将提供一些解决办法,希望能提供实战价值,让爬虫任务顺利完…...
)
小研究 - 主动式微服务细粒度弹性缩放算法研究(一)
微服务架构已成为云数据中心的基本服务架构。但目前关于微服务系统弹性缩放的研究大多是基于服务或实例级别的水平缩放,忽略了能够充分利用单台服务器资源的细粒度垂直缩放,从而导致资源浪费。为此,本文设计了主动式微服务细粒度弹性缩放算法…...

【LeetCode】215.数组中的第K个最大元素
题目 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。 请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。 你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1: 输入: [3,2,1,5,6,4…...

MySQL学习记录:第七章 存储过程和函数
文章目录 第七章 存储过程和函数一、存储过程1、 创建语法*2、调用语法(1)空参列表(2)创建带in参数模式的存储过程,需终端运行(3)创建带out参数模式的存储过程,需终端运行(4)创建带inout参数模式的存储过程,需终端运行3、删除存储过程4、查看存储过程的信息二、函数…...
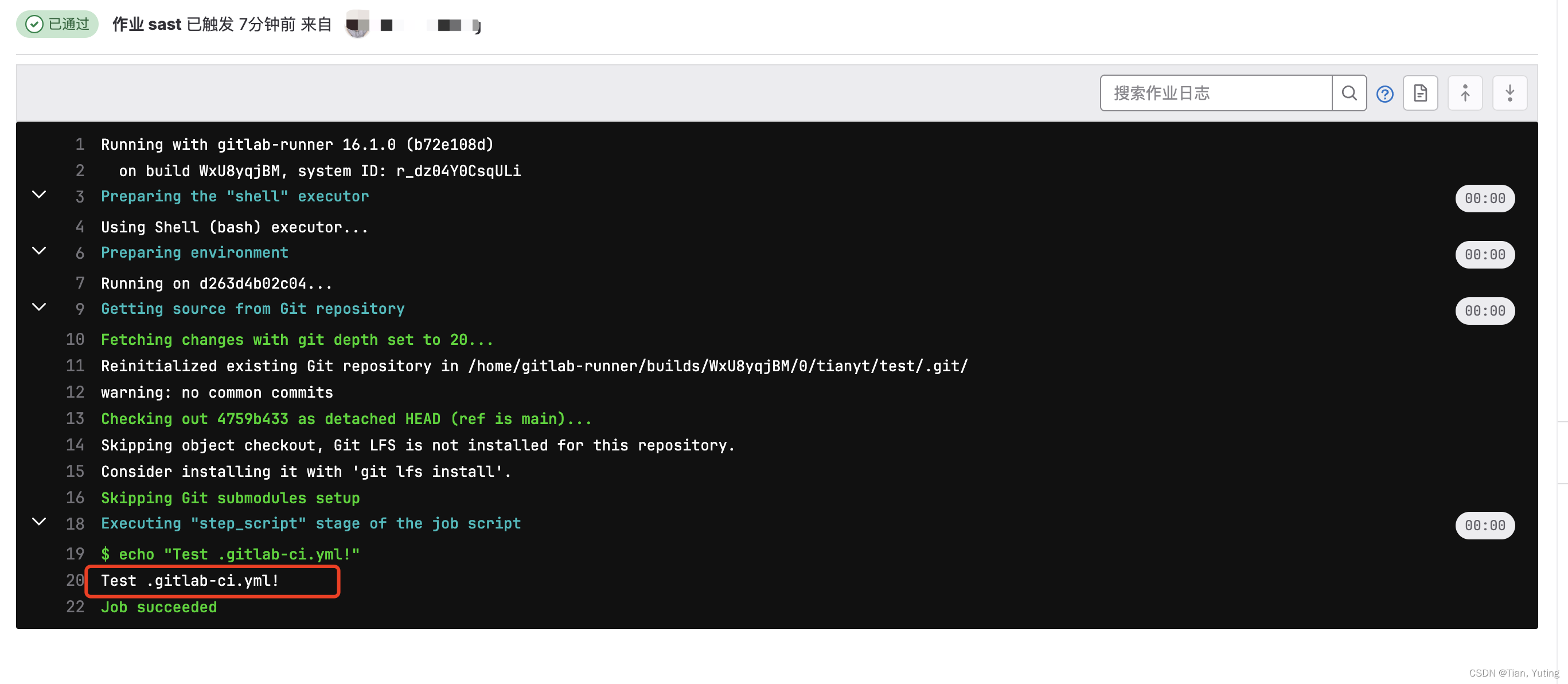
Docker中gitlab以及gitlab-runner的安装与使用
1、本文主要讲述如何使用Docker安装gitlab以及gitlab-runner,并且会讲述gitlab-runner如何使用 2、gitlab部分不需要修改过多的配置即可使用,本文未讲述https配置,如有需求,可自行百度 3、Docker如何安装可以自行百度 一、Docker安…...
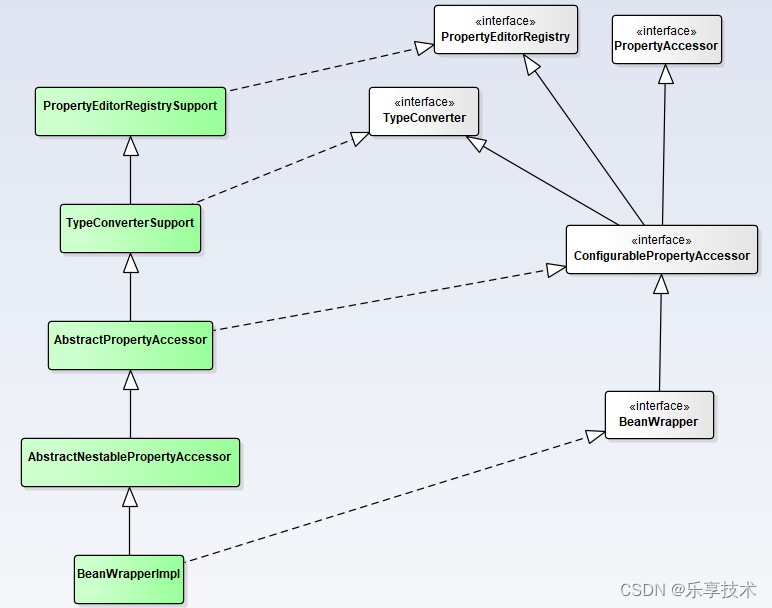
一起学SF框架系列5.12-spring-beans-数据绑定dataBinding
数据绑定有助于将用户输入动态绑定到应用程序的域模型(或用于处理用户输入的任何对象),主要用于web层,但实际可用于任何层。Spring提供了DataBinder来做到这一点,并提供了Validator进行数据验证,两者组成了…...

火热报名中 | 赛宁独家技术支持第七届“蓝帽杯”网络安全技能大赛
由公安部网络安全保卫局、教育部教育管理信息中心、中国教育协会指导,中国人民公安大学主办,奇安信科技集团股份有限公司协办,南京赛宁信息技术有限公司提供技术支持的2023第七届“蓝帽杯”全国大学生网络安全技能大赛于近日正式开启报名。 …...

无涯教程-jQuery - Ajax Tutorial函数
AJAX是用于创建交互式Web应用程序的Web开发技术。如果您了解JavaScript,HTML,CSS和XML,则只需花费一个小时即可开始使用AJAX。 为什么要学习Ajax? AJAX代表 A 同步 Ja vaScript和 X ML。 AJAX是一项新技术,可借助XML,HTML,CSS和Java Script创建更好,更快,更具交互性的Web应用…...

Android日志
Android中的日志工具类是Log(android.util.Log),这个类中提供了如下5个方法来供我们打印日志。 Log.v()。用于打印那些最为琐碎的、意义最小的日志信息。对应级别verbose,是Android日志里面级别最低的一种。 Log.d()。用于打印一…...

【Golang 接口自动化08】使用标准库httptest完成HTTP请求的Mock测试
目录 前言 http包的HandleFunc函数 http.Request/http.ResponseWriter httptest 定义被测接口 测试代码 测试执行 总结 资料获取方法 前言 Mock是一个做自动化测试永远绕不过去的话题。本文主要介绍使用标准库net/http/httptest完成HTTP请求的Mock的测试方法。 可能有…...

SpringBoot自定义注解 + AOP+分布式Redis 防止重复提交
第一步 引入依赖pom.xml: <dependency><groupId>org.redisson</groupId><artifactId>redisson</artifactId><version>3.16.3</version> <!-- 使用最新版本 --></dependency><dependency><groupId&g…...

3.yum安装分布式LNMP--剧本
文章目录 修改hosts创建剧本文件 修改hosts vim /etc/ansible/hosts[webservers] 192.168.242.67[dbservers] 192.168.242.68[phpservers] 192.168.242.69创建剧本文件 vim lnmp.yaml- name: nginx playhosts: webserversremote_user: rootvars:- http_port: 192.168.242.67:…...
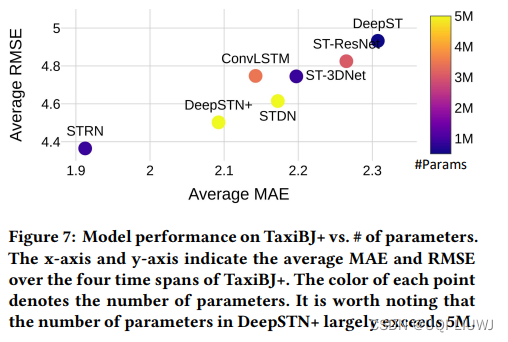
论文笔记:Fine-Grained Urban Flow Prediction
2021 WWW 1 intro 细粒度城市流量预测 两个挑战 细粒度数据中观察到的网格间的转移动态使得预测变得更加复杂 需要在全局范围内捕获网格单元之间的空间依赖性单独学习外部因素(例如天气、POI、路段信息等)对大量网格单元的影响非常具有挑战性——>论…...
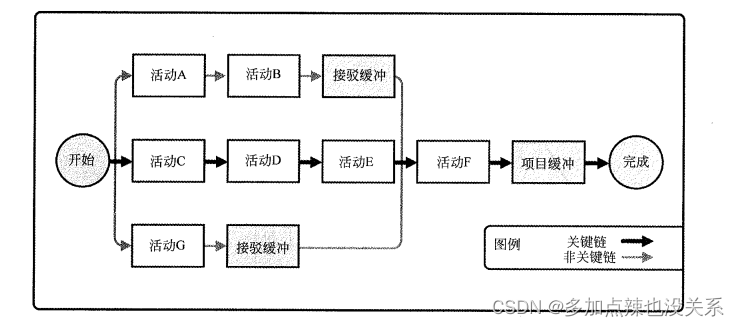
系统集成|第八章(笔记)
目录 第八章 进度管理8.1 主要过程8.1.1 规划进度管理8.1.2 定义活动8.1.3 排列活动顺序8.1.4 估算活动资源8.1.5 估算活动持续时间8.1.6 制定进度计划8.1.7 控制进度 8.2 注意与问题 上篇:第七章、范围管理 第八章 进度管理 8.1 主要过程 包括: 规划进…...

【分布式】分布式唯一 ID 的 几种生成方案以及优缺点snowflake优化方案
在互联网的业务系统中,涉及到各种各样的ID,如在支付系统中就会有支付ID、退款ID等。那一般生成ID都有哪些解决方案呢?特别是在复杂的分布式系统业务场景中,我们应该采用哪种适合自己的解决方案是十分重要的。下面我们一一来列举一…...

FFmpeg5.0源码阅读——av_interleaved_write_frame
摘要:本文主要详细描述FFmpeg中封装时写packet到媒体文件的函数av_interleaved_write_frame的实现。 关键字:av_interleaved_write_frame 读者须知:读者需要熟悉ffmpeg的基本使用。 1 基本调用流程 av_interleaved_write_frame的基本…...

力扣 70. 爬楼梯
题目来源:https://leetcode.cn/problems/climbing-stairs/description/ C题解(来源代码随想录): 本质上是一道斐波那契数题。 动规五部曲:定义一个一维数组来记录不同楼层的状态 确定dp数组以及下标的含义。dp[i]&am…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
