【LeetCode】215.数组中的第K个最大元素
题目
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4],k = 2 输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4 输出: 4
提示:
1 <= k <= nums.length <= 10^5-10^4 <= nums[i] <= 10^4
解答
源代码
class Solution {Random rand = new Random();public int findKthLargest(int[] nums, int k) {return quickSelect(nums, k, 0, nums.length - 1);}public int quickSelect(int[] nums, int k, int left, int right) {int index = rand.nextInt(right - left + 1) + left;// 目标值int target = nums[index];// 因为在之后交换元素中,nums[left]的值会被覆盖,所以这里把nums[index]记为nums[left]的值nums[index] = nums[left];int i = left, j = right;while (i < j) {while (i < j && nums[j] <= target) {j--;}nums[i] = nums[j];while (i < j && nums[i] >= target) {i++;}nums[j] = nums[i];}// 此时nums[i]前的元素都比目标值大,nums[i]之后的元素都比目标值小nums[i] = target;if (i == k - 1) {return nums[i];} else if (i < k - 1) {return quickSelect(nums, k, i + 1, right);} else {return quickSelect(nums, k, left, i - 1);}}
}总结
这道题写得我好痛苦……因为后面的测试案例有极端情况,所以一定要用到随机,又因为用到了随机,所以和排序算法不是完全一样,不能直接进行交换,否则最后相遇的那个数和目标值交换后的数组不一定是合法的(目标值前面都是大于它的数,后面都是小于它的数)。
相关文章:

【LeetCode】215.数组中的第K个最大元素
题目 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。 请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。 你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1: 输入: [3,2,1,5,6,4…...

MySQL学习记录:第七章 存储过程和函数
文章目录 第七章 存储过程和函数一、存储过程1、 创建语法*2、调用语法(1)空参列表(2)创建带in参数模式的存储过程,需终端运行(3)创建带out参数模式的存储过程,需终端运行(4)创建带inout参数模式的存储过程,需终端运行3、删除存储过程4、查看存储过程的信息二、函数…...
Docker中gitlab以及gitlab-runner的安装与使用
1、本文主要讲述如何使用Docker安装gitlab以及gitlab-runner,并且会讲述gitlab-runner如何使用 2、gitlab部分不需要修改过多的配置即可使用,本文未讲述https配置,如有需求,可自行百度 3、Docker如何安装可以自行百度 一、Docker安…...
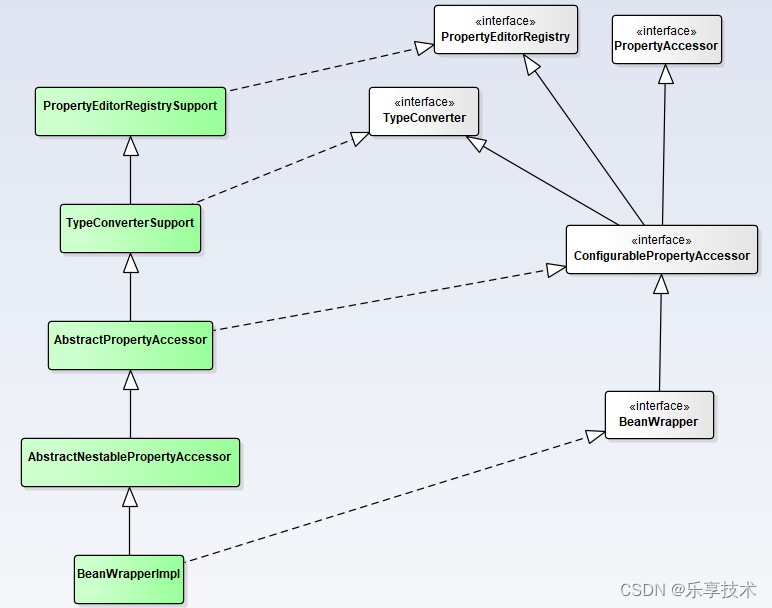
一起学SF框架系列5.12-spring-beans-数据绑定dataBinding
数据绑定有助于将用户输入动态绑定到应用程序的域模型(或用于处理用户输入的任何对象),主要用于web层,但实际可用于任何层。Spring提供了DataBinder来做到这一点,并提供了Validator进行数据验证,两者组成了…...

火热报名中 | 赛宁独家技术支持第七届“蓝帽杯”网络安全技能大赛
由公安部网络安全保卫局、教育部教育管理信息中心、中国教育协会指导,中国人民公安大学主办,奇安信科技集团股份有限公司协办,南京赛宁信息技术有限公司提供技术支持的2023第七届“蓝帽杯”全国大学生网络安全技能大赛于近日正式开启报名。 …...

无涯教程-jQuery - Ajax Tutorial函数
AJAX是用于创建交互式Web应用程序的Web开发技术。如果您了解JavaScript,HTML,CSS和XML,则只需花费一个小时即可开始使用AJAX。 为什么要学习Ajax? AJAX代表 A 同步 Ja vaScript和 X ML。 AJAX是一项新技术,可借助XML,HTML,CSS和Java Script创建更好,更快,更具交互性的Web应用…...

Android日志
Android中的日志工具类是Log(android.util.Log),这个类中提供了如下5个方法来供我们打印日志。 Log.v()。用于打印那些最为琐碎的、意义最小的日志信息。对应级别verbose,是Android日志里面级别最低的一种。 Log.d()。用于打印一…...

【Golang 接口自动化08】使用标准库httptest完成HTTP请求的Mock测试
目录 前言 http包的HandleFunc函数 http.Request/http.ResponseWriter httptest 定义被测接口 测试代码 测试执行 总结 资料获取方法 前言 Mock是一个做自动化测试永远绕不过去的话题。本文主要介绍使用标准库net/http/httptest完成HTTP请求的Mock的测试方法。 可能有…...

SpringBoot自定义注解 + AOP+分布式Redis 防止重复提交
第一步 引入依赖pom.xml: <dependency><groupId>org.redisson</groupId><artifactId>redisson</artifactId><version>3.16.3</version> <!-- 使用最新版本 --></dependency><dependency><groupId&g…...

3.yum安装分布式LNMP--剧本
文章目录 修改hosts创建剧本文件 修改hosts vim /etc/ansible/hosts[webservers] 192.168.242.67[dbservers] 192.168.242.68[phpservers] 192.168.242.69创建剧本文件 vim lnmp.yaml- name: nginx playhosts: webserversremote_user: rootvars:- http_port: 192.168.242.67:…...
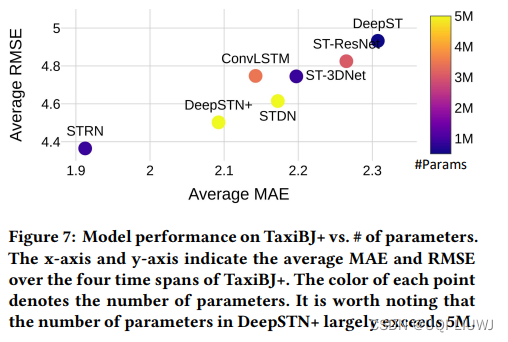
论文笔记:Fine-Grained Urban Flow Prediction
2021 WWW 1 intro 细粒度城市流量预测 两个挑战 细粒度数据中观察到的网格间的转移动态使得预测变得更加复杂 需要在全局范围内捕获网格单元之间的空间依赖性单独学习外部因素(例如天气、POI、路段信息等)对大量网格单元的影响非常具有挑战性——>论…...
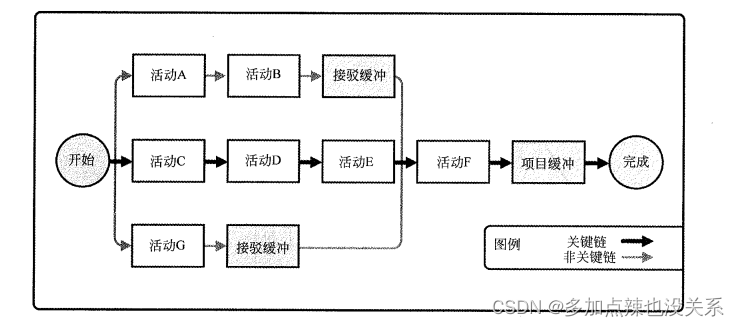
系统集成|第八章(笔记)
目录 第八章 进度管理8.1 主要过程8.1.1 规划进度管理8.1.2 定义活动8.1.3 排列活动顺序8.1.4 估算活动资源8.1.5 估算活动持续时间8.1.6 制定进度计划8.1.7 控制进度 8.2 注意与问题 上篇:第七章、范围管理 第八章 进度管理 8.1 主要过程 包括: 规划进…...

【分布式】分布式唯一 ID 的 几种生成方案以及优缺点snowflake优化方案
在互联网的业务系统中,涉及到各种各样的ID,如在支付系统中就会有支付ID、退款ID等。那一般生成ID都有哪些解决方案呢?特别是在复杂的分布式系统业务场景中,我们应该采用哪种适合自己的解决方案是十分重要的。下面我们一一来列举一…...

FFmpeg5.0源码阅读——av_interleaved_write_frame
摘要:本文主要详细描述FFmpeg中封装时写packet到媒体文件的函数av_interleaved_write_frame的实现。 关键字:av_interleaved_write_frame 读者须知:读者需要熟悉ffmpeg的基本使用。 1 基本调用流程 av_interleaved_write_frame的基本…...

力扣 70. 爬楼梯
题目来源:https://leetcode.cn/problems/climbing-stairs/description/ C题解(来源代码随想录): 本质上是一道斐波那契数题。 动规五部曲:定义一个一维数组来记录不同楼层的状态 确定dp数组以及下标的含义。dp[i]&am…...

AVFoundation - 媒体捕捉
文章目录 注意使用 NSCameraUsageDescriptioniOS 的摄像头可能比 Mac 更多功能特性@interface Capture ()<AVCaptureFileOutputRecordingDelegate>@property (strong, nonatomic) AVCaptureSession *captureSession; @property (weak, nonatomic) AVCaptureDeviceInput *…...
【新版系统架构补充】-嵌入式技术
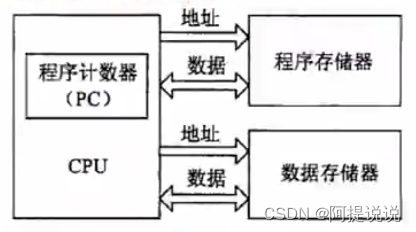
嵌入式微处理体系结构 冯诺依曼结构 传统计算机采用冯诺依曼结构,也称普林斯顿结构,是一种将程序指令存储器和数据存储器合并在一起的存储器结构 冯诺依曼的计算机程序和数据共用一个存储空间,程序指令存储地址和数据存储地址指向同一个存…...
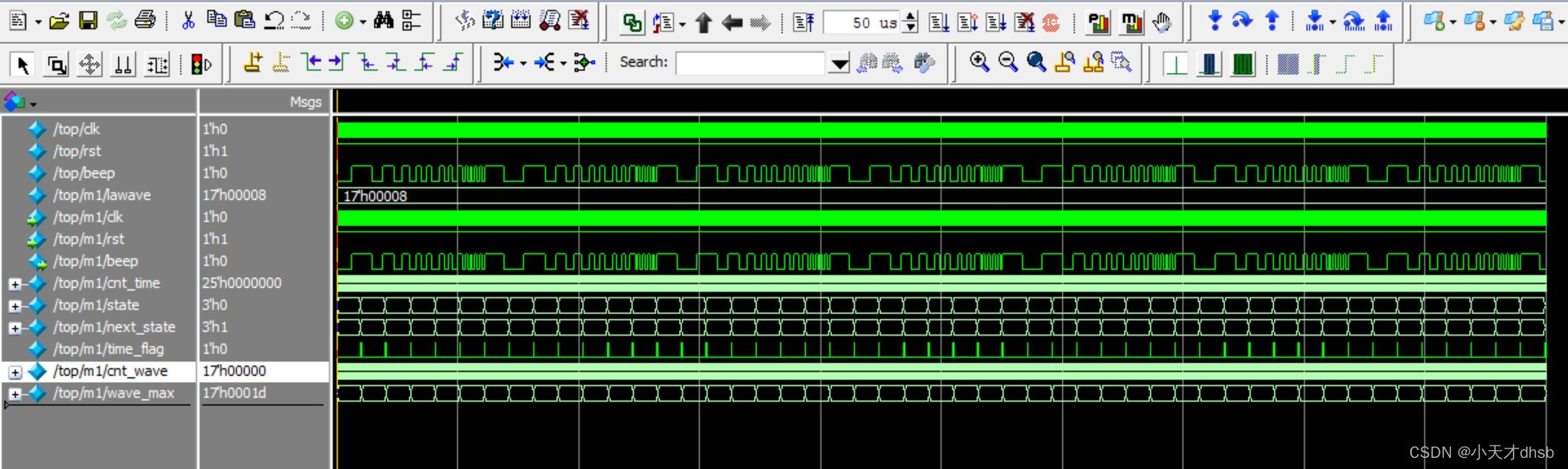
fpga开发--蜂鸣器发出连续不同的音调
描述 使用fpga蜂鸣器连续发出do,re,mi,fa,so,la,xi七个不同的音调,每个音调的持续时间为0.5s。 思路 采用状态机实现音调的转化,当do状态持续了0.5s之后转移到re状态,…...
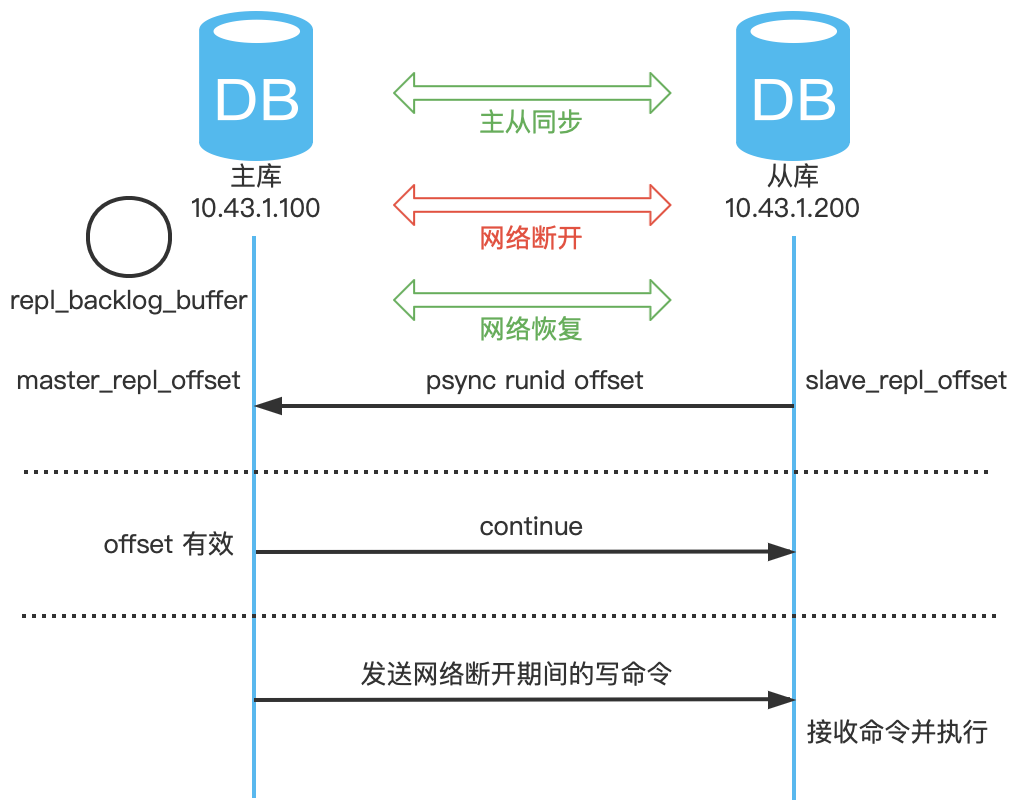
Redis 主从同步原理
一、什么是主从同步? 主从同步,就是将数据冗余备份,主库(Master)将自己库中的数据,同步给从库(Slave)。 从库可以一个,也可以多个,如图所示: 二…...
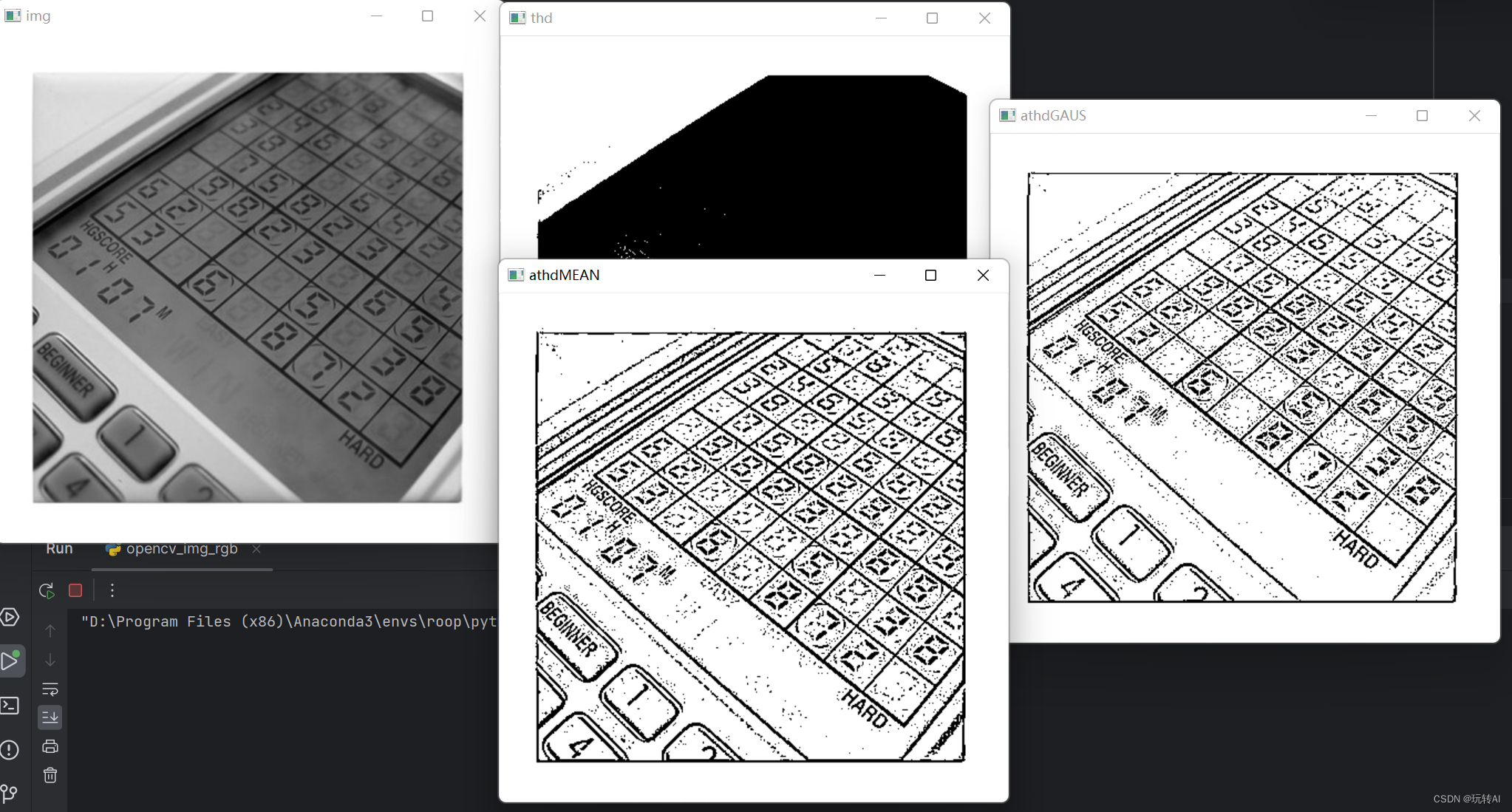
opencv-28 自适应阈值处理-cv2.adaptiveThreshold()
什么是自适应阈值处理? 对于色彩均衡的图像,直接使用一个阈值就能完成对图像的阈值化处理。但是,有时图像的色彩是不均衡的,此时如果只使用一个阈值,就无法得到清晰有效的阈值分割结果图像。 有一种改进的阈值处理技术ÿ…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...

生信服务器 | 做生信为什么推荐使用Linux服务器?
原文链接:生信服务器 | 做生信为什么推荐使用Linux服务器? 一、 做生信为什么推荐使用服务器? 大家好,我是小杜。在做生信分析的同学,或是将接触学习生信分析的同学,<font style"color:rgb(53, 1…...
