平板光波导中导模的(注意不是泄露模)传播常数β的matlab计算(验证了是对的)
参照的是导波光学_王建(清华大学)的公式(3-1-2、3-1-3),算的参数是这本书的图3-3的。
function []=PropagationConstantsMain()
clear;clc;close all
lambda0=1.55;%真空或空气中的入射波长,单位um
k0=2*pi/lambda0;
m=3;%导模阶数(需要人为指定)
n1=1.62;%芯区的折射率
n2=1.515;%衬底的折射率
n3=1;%包层的折射率
w=5;%芯区厚度,单位um
TEorTM='TE';%选定极化
beta0=linspace(k0*n2+1e-5,k0*n1-1e-5,500);%导模的传播常数范围(根据公式自动得出)%=================%
Fun=@(x)EigEq(x,k0,n1,n2,n3,m,w,TEorTM);
%=================%figure
y=arrayfun(Fun,beta0);
plot(beta0,y,'ro','MarkerSize',2)
hold on
plot(beta0,zeros(1,length(beta0)),'k--')
hold off
axis tight
xlabel('\beta')if strcmp(TEorTM,'TE')==1%TEtitle('TE')
elseif strcmp(TEorTM,'TM')==1%TMtitle('TM')
endop=fzero(Fun,[beta0(1),beta0(end)]);
disp([TEorTM,'极化下',num2str(m),'阶导模的传播常数为:',num2str(op),' (注意单位)'])endfunction [oup]=EigEq(beta,k0,n1,n2,n3,m,w,TEorTM)
%beta未知
%m是导模阶数
%w是膜(芯区)厚
k=((k0*n1)^2-beta^2)^(1/2);
P=(beta^2-(k0*n2)^2)^(1/2);
q=(beta^2-(k0*n3)^2)^(1/2);if strcmp(TEorTM,'TE')==1%TEoup=k*w-m*pi-atan(P/k)-atan(q/k);elseif strcmp(TEorTM,'TM')==1%TMoup=k*w-m*pi-atan(P/k*((n1/n2)^2))-atan(q/k*((n1/n3)^2));
endend
做了笔记的PDF图书:https://petmask.lanzoub.com/i9x3W13pnore

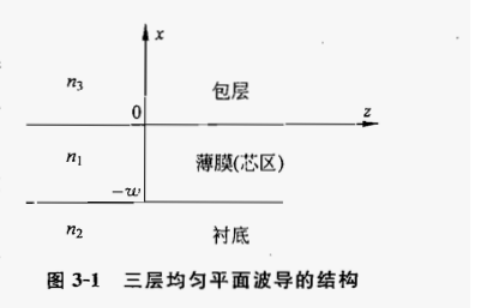
注意波导沿着光波传播方向(z向)是无限长的。
Slab waveguide的色散图的计算(未详细验证正确性)
function []=SlabWaveguideDispersionMain()
clear;clc;close all
c_const=299792458;%m/s
lambda0=linspace(0.9,2,1000);%真空或空气中的入射波长范围(人为指定),单位um
k0=2*pi./lambda0;%行数组
w0=c_const.*k0;%行数组
%m=3;%导模阶数(需要人为指定)
n1=2;%芯区的折射率
n2=1;%衬底的折射率
n3=1;%包层的折射率
w=0.75;%芯区厚度,单位um
TEorTM='TE';%选定极化%============%
figure%限定了导模的范围
plot(w0,n2.*k0,'k--')
hold on
plot(w0,n1.*k0,'k--')
hold on
%============%m0sto=zeros(length(k0),1);%列数组
m1sto=zeros(length(k0),1);%列数组
m2sto=zeros(length(k0),1);%列数组
m3sto=zeros(length(k0),1);%列数组
m4sto=zeros(length(k0),1);%列数组
k0=k0.';%列数组
parfor jj=1:length(k0)Mark=jj/length(k0)K0=k0(jj,1);beta0=linspace(K0*n2+1e-5,K0*n1-1e-5,500).';%导模的传播常数范围(根据公式自动得出)%=================%
m=0;
Fun=@(x)EigEq(x,K0,n1,n2,n3,m,w,TEorTM);
if sign(EigEq(beta0(1),K0,n1,n2,n3,m,w,TEorTM))==sign(EigEq(beta0(end),K0,n1,n2,n3,m,w,TEorTM))m0sto(jj,1)=0;elsem0sto(jj,1)=fzero(Fun,[beta0(1),beta0(end)]);
end
%=================%%=================%
m=1;
Fun=@(x)EigEq(x,K0,n1,n2,n3,m,w,TEorTM);
if sign(EigEq(beta0(1),K0,n1,n2,n3,m,w,TEorTM))==sign(EigEq(beta0(end),K0,n1,n2,n3,m,w,TEorTM))m1sto(jj,1)=0;elsem1sto(jj,1)=fzero(Fun,[beta0(1),beta0(end)]);
end
%=================%%=================%
m=2;
Fun=@(x)EigEq(x,K0,n1,n2,n3,m,w,TEorTM);
if sign(EigEq(beta0(1),K0,n1,n2,n3,m,w,TEorTM))==sign(EigEq(beta0(end),K0,n1,n2,n3,m,w,TEorTM))m2sto(jj,1)=0;elsem2sto(jj,1)=fzero(Fun,[beta0(1),beta0(end)]);
end
%=================%%=================%
m=3;
Fun=@(x)EigEq(x,K0,n1,n2,n3,m,w,TEorTM);
if sign(EigEq(beta0(1),K0,n1,n2,n3,m,w,TEorTM))==sign(EigEq(beta0(end),K0,n1,n2,n3,m,w,TEorTM))m3sto(jj,1)=0;elsem3sto(jj,1)=fzero(Fun,[beta0(1),beta0(end)]);
end
%=================%%=================%
m=4;
Fun=@(x)EigEq(x,K0,n1,n2,n3,m,w,TEorTM);
if sign(EigEq(beta0(1),K0,n1,n2,n3,m,w,TEorTM))==sign(EigEq(beta0(end),K0,n1,n2,n3,m,w,TEorTM))m4sto(jj,1)=0;elsem4sto(jj,1)=fzero(Fun,[beta0(1),beta0(end)]);
end
%=================%endM0=[w0.',m0sto];M0(M0(:,2)==0,:)=[];
M1=[w0.',m1sto];M1(M1(:,2)==0,:)=[];
M2=[w0.',m2sto];M2(M2(:,2)==0,:)=[];
M3=[w0.',m3sto];M3(M3(:,2)==0,:)=[];
M4=[w0.',m4sto];M4(M4(:,2)==0,:)=[];scatter(M0(:,1),M0(:,2),10,'ro');
hold on
scatter(M1(:,1),M1(:,2),10,'ko');
hold on
scatter(M2(:,1),M2(:,2),10,'bo');
hold on
scatter(M3(:,1),M3(:,2),10,'yo');
hold on
scatter(M4(:,1),M4(:,2),10,'kd');
hold off
legend('','','m0','m1','m2','m3','m4')if strcmp(TEorTM,'TE')==1%TEtitle('TE')
elseif strcmp(TEorTM,'TM')==1%TMtitle('TM')
end
xlabel('\omega_{0}')
ylabel('\beta')
axis tight
%disp([TEorTM,'极化下',num2str(m),'阶导模的传播常数为:',num2str(op),' (注意单位)'])%============%
figure%限定了导模的范围
plot(lambda0,n2.*k0,'k--')
hold on
plot(lambda0,n1.*k0,'k--')
hold on
%============%
M0=[lambda0.',m0sto];M0(M0(:,2)==0,:)=[];
M1=[lambda0.',m1sto];M1(M1(:,2)==0,:)=[];
M2=[lambda0.',m2sto];M2(M2(:,2)==0,:)=[];
M3=[lambda0.',m3sto];M3(M3(:,2)==0,:)=[];
M4=[lambda0.',m4sto];M4(M4(:,2)==0,:)=[];scatter(M0(:,1),M0(:,2),10,'ro');
hold on
scatter(M1(:,1),M1(:,2),10,'ko');
hold on
scatter(M2(:,1),M2(:,2),10,'bo');
hold on
scatter(M3(:,1),M3(:,2),10,'yo');
hold on
scatter(M4(:,1),M4(:,2),10,'kd');
hold off
legend('','','m0','m1','m2','m3','m4')if strcmp(TEorTM,'TE')==1%TEtitle('TE')
elseif strcmp(TEorTM,'TM')==1%TMtitle('TM')
end
xlabel('\lambda_{0}(um)')
ylabel('\beta')
axis tightendfunction [oup]=EigEq(beta,k0,n1,n2,n3,m,w,TEorTM)
%beta未知
%m是导模阶数
%w是膜(芯区)厚
k=((k0*n1)^2-beta^2)^(1/2);
P=(beta^2-(k0*n2)^2)^(1/2);
q=(beta^2-(k0*n3)^2)^(1/2);if strcmp(TEorTM,'TE')==1%TEoup=k*w-m*pi-atan(P/k)-atan(q/k);elseif strcmp(TEorTM,'TM')==1%TMoup=k*w-m*pi-atan(P/k*((n1/n2)^2))-atan(q/k*((n1/n3)^2));
endend
第一个代码加了算有效折射率的
function []=PropagationConstantsMain()
clear;clc;close all
lambda0=9.608016155617717;%真空或空气中的入射波长,单位um
k0=2*pi/lambda0;
m=0;%导模阶数(需要人为指定)
n1=3;%芯区的折射率
n2=1;%衬底的折射率
n3=1;%包层的折射率
w=0.27;%芯区厚度,单位um
TEorTM='TE';%选定极化
beta0=linspace(k0*n2+1e-5,k0*n1-1e-5,500);%导模的传播常数范围(根据公式自动得出)%=================%
Fun=@(x)EigEq(x,k0,n1,n2,n3,m,w,TEorTM);
%=================%figure
y=arrayfun(Fun,beta0);
plot(beta0,y,'ro','MarkerSize',2)
hold on
plot(beta0,zeros(1,length(beta0)),'k--')
hold off
axis tight
xlabel('\beta')if strcmp(TEorTM,'TE')==1%TEtitle('TE')
elseif strcmp(TEorTM,'TM')==1%TMtitle('TM')
endop=fzero(Fun,[beta0(1),beta0(end)]);
disp([TEorTM,'极化下',num2str(m),'阶导模的传播常数为:',num2str(op),' (注意单位)'])
disp([TEorTM,'极化下',num2str(m),'阶导模的有效折射率为:',num2str(op/k0)])endfunction [oup]=EigEq(beta,k0,n1,n2,n3,m,w,TEorTM)
%beta未知
%m是导模阶数
%w是膜(芯区)厚
k=((k0*n1)^2-beta^2)^(1/2);
P=(beta^2-(k0*n2)^2)^(1/2);
q=(beta^2-(k0*n3)^2)^(1/2);if strcmp(TEorTM,'TE')==1%TEoup=k*w-m*pi-atan(P/k)-atan(q/k);elseif strcmp(TEorTM,'TM')==1%TMoup=k*w-m*pi-atan(P/k*((n1/n2)^2))-atan(q/k*((n1/n3)^2));
endend
相关文章:

平板光波导中导模的(注意不是泄露模)传播常数β的matlab计算(验证了是对的)
参照的是导波光学_王建(清华大学)的公式(3-1-2、3-1-3),算的参数是这本书的图3-3的。 function []PropagationConstantsMain() clear;clc;close all lambda01.55;%真空或空气中的入射波长,单位um k02*pi/lambda0; m3;%导模阶数(需要人为指定) n11.62;%芯…...

JVM面试题--JVM组成
JVM是什么 Java Virtual Machine Java程序的运行环境(java二进制字节码的运行环境) 运行流程 什么是程序计数器? 程序计数器:线程私有的,内部保存的字节码的行号。用于记录正在执行的字节码指令的地址。 我们知道ja…...

【Golang 接口自动化05】使用yml管理自动化用例
目录 YAML 基本语法 对象:键值对的集合(key:value) 数组:一组按顺序排列的值 字面量:单个的、不可再分的值(数字、字符串、布尔值) yml 格式的测试用例 定义yml文件 创建结构体 读取yml文件中的用例数据 调试…...
【【STM32学习-3】】
STM32学习-3 下面是对c语言的稍微复习 这个是我们设置好的文件 以后拖出去用就可以了 这里加入关于指针的感想 关于指针数组和数组指针的想法 常规的东西是int a10; int * p&a; (p指向了a元素,意思是p等于a的地址 类型是int*)就是 整型指…...
代码随想录第四十八天|198、213、337.打家劫舍
198.打家劫舍 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。 给定一个代表每个…...

js笔记总结
prototype 属性的作用 JavaScript 规定,每个函数都有一个prototype属性,指向一个对象。 function f() {} typeof f.prototype // "object" 上面代码中,函数f默认具有prototype属性,指向一个对象。 对于普通函数来…...
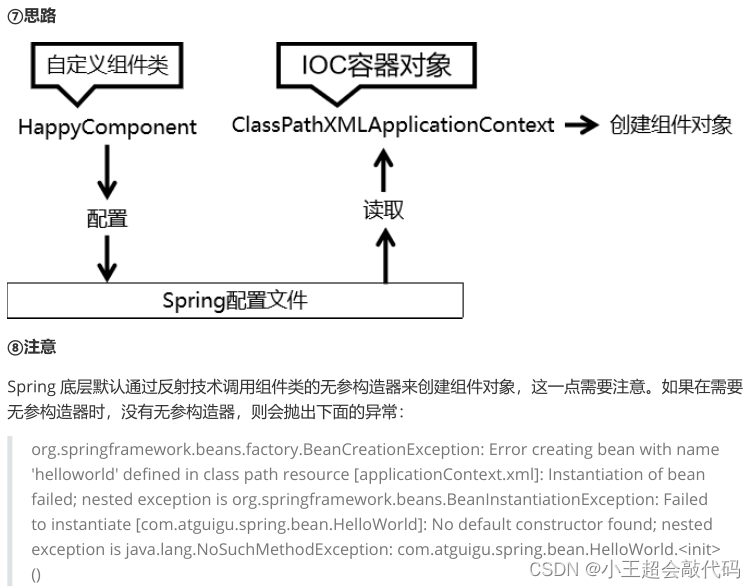
第四章:Spring上
第四章:Spring上 4.1:Spring简介 Spring概述 官网地址:https://spring.io/。 Spring是最受欢迎的企业级的java应用程序开发框架,数以百万的来自世界各地的开发人员使用Spring框架来创建性能好、易于测试、可重用的代码。Spring框…...
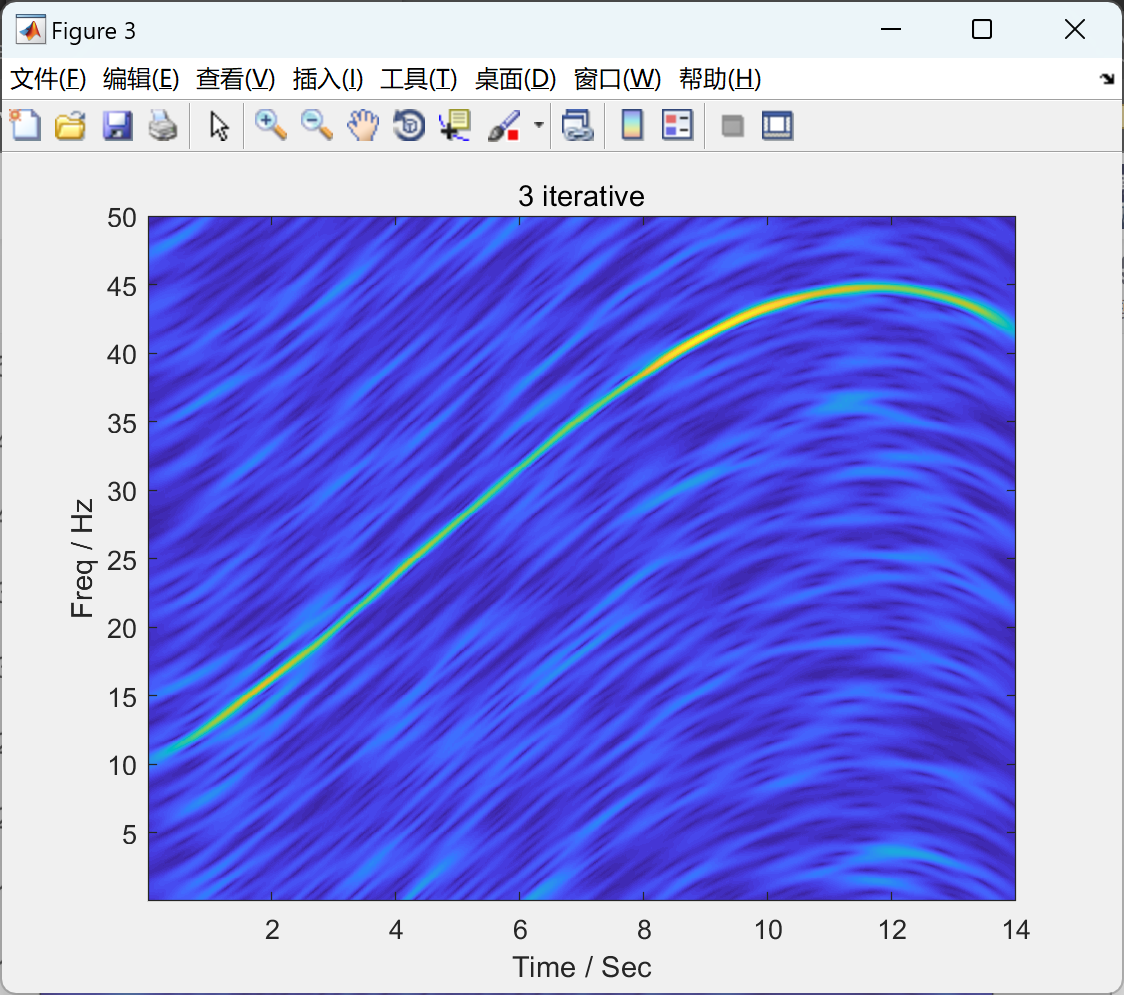
【时频分析,非线性中频】非线性STFT在瞬时频率估计中的应用(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
)
MTK平台关机流程和原因(二)
(1)ShutdownThread 从上一篇可以看到,最终会调用此类的shutdown以及reboot等函数,我们来看一下这些函数的实现。 (A)被调用函数 //frameworks/base/services/core/java/com/android/server/power/Shutdo…...

【Python】pyqt6入门到入土系列,非常详细...
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 一、什么是PyQt6? 简单介绍一下PyQt6 1、基础简介 PyQt6 Digia 公司的 Qt 程序的 Python 中间件。Qt库是最强大的GUI库之一。 PyQt6的官网:www.riverbankcomputing.co.uk/news。 PyQt6是由Riverbank Co…...

TCP socket编程
一、服务端代码 #encoding utf -8 #导入socket库 from socket import * #等待客户端来连接,主机地址为0.0.0.0表示绑定本机所有网络接口ip地址 IP 0.0.0.0 #端口号 PORT 50000 #定义一次从socket缓存区最多读入512个字节数据 BUFLEN 512 #实例化一个socket编程…...

HTTP——一、了解Web及网络基础
HTTP 一、使用HTTP协议访问Web二、HTTP的诞生1、为知识共享而规划Web2、Web成长时代3、驻足不前的HTTP 三、网络基础TCP/IP1、TCP/IP协议族2、TCP/IP的分层管理3、TCP/IP 通信传输流 四、与HTTP关系密切的协议:IP、TCP和DNS1、负责传输的 IP 协议2、确保可靠性的TCP…...

[论文笔记] chatgpt系列 2.6 DeepSpeed-chat 数据集
一、FT数据集 & Reward model数据集 Deepspeed-chat 源代码的数据集: Dahoas/rm-static: 这是一个用于强化学习的静态环境数据集,包含了一个机器人在一个固定环境中的运动轨迹。该数据集旨在用于评估强化学习算法在静态环境下的表现。 Dahoas/full-hh-rlhf: 这是一个用于…...
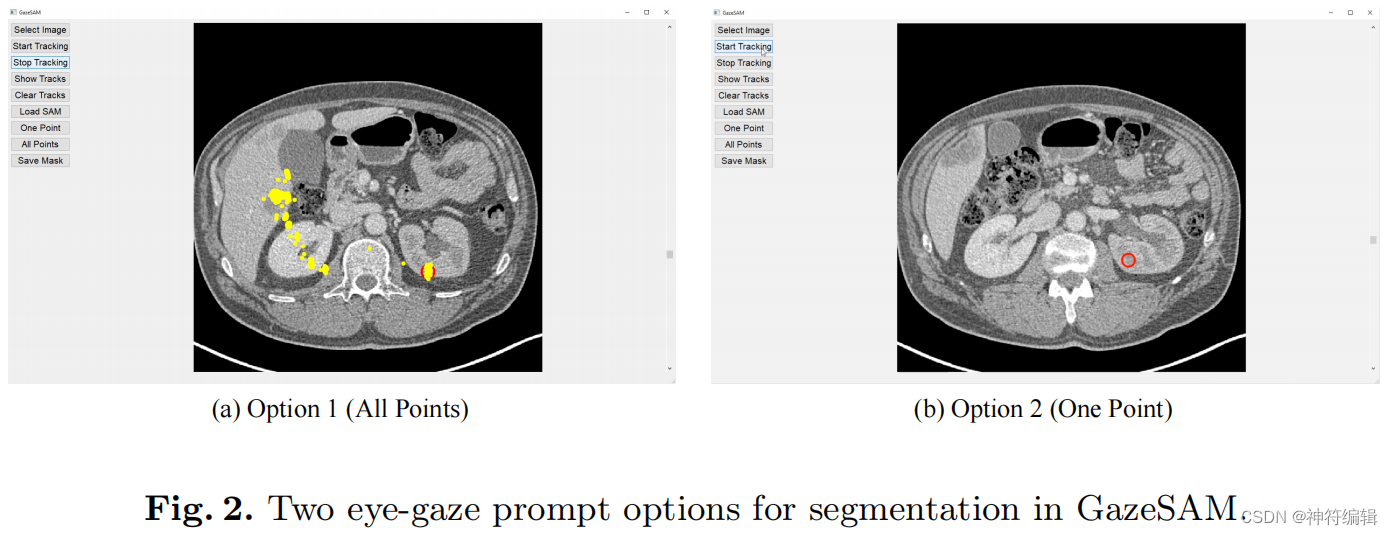
探究SAM和眼球追踪技术在自动医学图像分割的应用(2023+GazeSAM: What You See is What You Segment)
摘要: 本研究探讨眼动追踪技术与SAM的潜力,以设计一个协同的人机交互系统,自动化医学图像分割。提出了GazeSAM系统,使放射科医生能够在图像诊断过程中通过简单地查看感兴趣的区域来收集分割掩模。该系统跟踪放射科医生的眼球运动…...
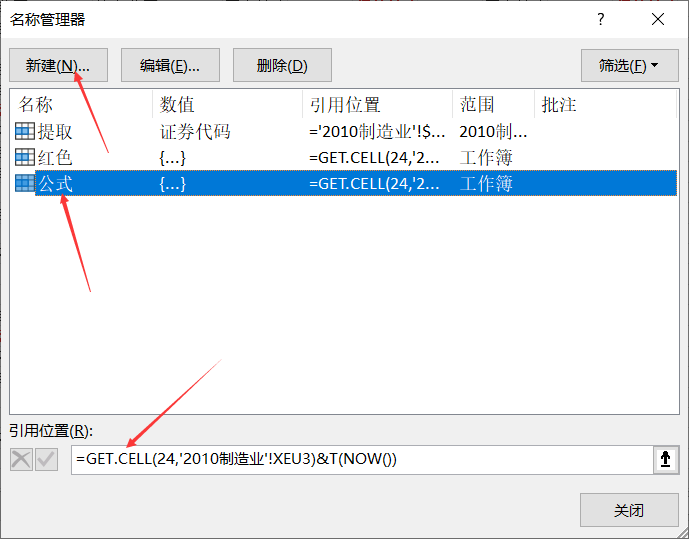
excle中的条件求和SUMIF
问题:将每一行中红色文字的前一个值累计求和到境外总数这一列 使用的公式 自制单元格的格式计算公式:ctrlf3打开格式管理,创建如下公式,其中24是表示获取文字颜色 由于sumif只能直接与第二参数条件比较,所以先使用IF(公…...

python-网络爬虫.Request
Request python中requests库使用方法详解: 一简介: Requests 是Python语言编写,基于urllib, 采用Apache2 Licensed开源协议的 HTTP 库。 与urllib相比,Requests更加方便,处理URL资源特别流畅。 可以节约我…...
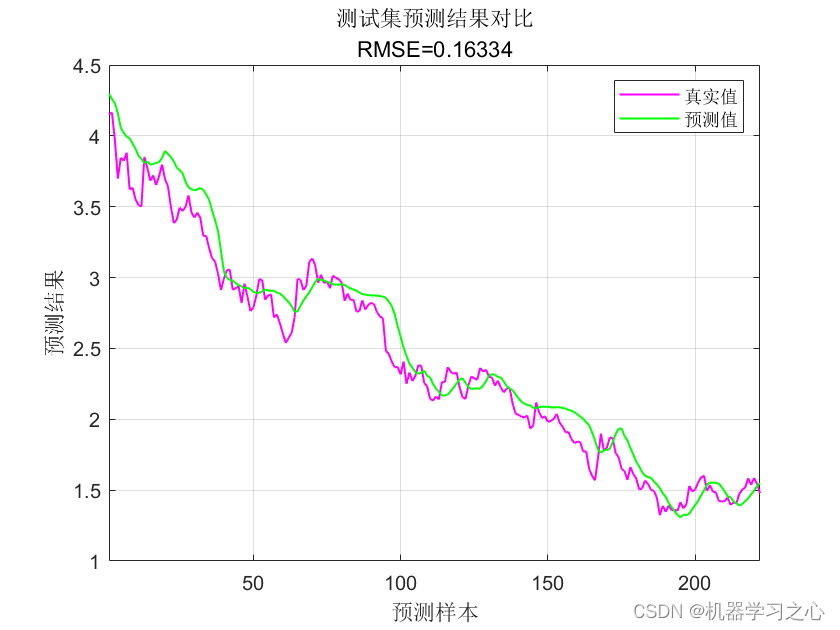
时序预测 | MATLAB实现GRNN广义回归神经网络时间序列预测(多指标,多图)
时序预测 | MATLAB实现GRNN广义回归神经网络时间序列预测(多指标,多图) 目录 时序预测 | MATLAB实现GRNN广义回归神经网络时间序列预测(多指标,多图)效果一览基本介绍程序设计参考资料效果一览 基本介绍 1.MATLAB实现GRNN广义回归神经网络时间序列预测(完整源码和数据) …...
如何看待低级爬虫与高级爬虫?
爬虫之所以分为高级和低级,主要是基于其功能、复杂性和灵活性的差异。根据我总结大概有下面几点原因: 功能和复杂性:高级爬虫通常提供更多功能和扩展性,包括处理复杂页面结构、模拟用户操作、解析和清洗数据等。它们解决了开发者…...

3.分支与循环
一、分支结构 1.概念 一个 CPP 程序默认是按照代码书写顺序,从上到下依次执行下来的。但是,有时我们需要选择性的执行某些语句,来实现更加复杂的逻辑,这时候就需要分支结构语句的功能来实现。选择合适的分支语句可以显著提高程序…...
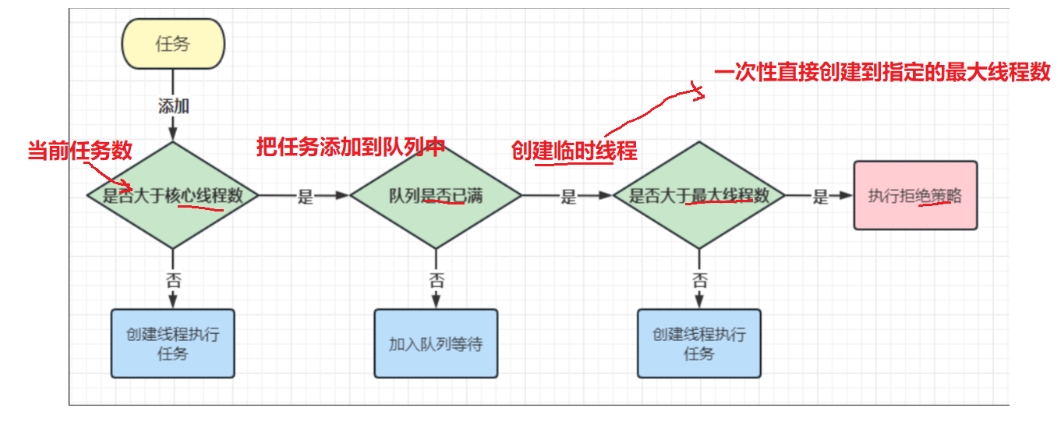
面试之多线程案例(四)
1.单例模式 单例模式是指在内存中只会创建且仅创建一次对象的设计模式。在程序中多次使用同一个对象且作用相同时,为了防止频繁地创建对象使得内存飙升,单例模式可以让程序仅在内存中创建一个对象,让所有需要调用的地方都共享这一单例对象。…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
