【时频分析,非线性中频】非线性STFT在瞬时频率估计中的应用(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
2.1 算例1
2.2 算例2
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
该文提出一种新的时频分析(TFA)方法,称为非线性STFT(NLSTFT)。一种有效的TFA方法,该方法可以用时变瞬时频率对信号进行记录。实际上,传统的TFA方法在处理此类信号时受到限制。
-
非线性STFT(Short-Time Fourier Transform)是一种在时频分析中常用的方法,它可以将信号在时间和频率上进行局部分析。非线性STFT在瞬时频率估计中的应用主要是用于分析非线性系统中的信号。
在非线性系统中,信号的频率可能会随时间变化,这就需要对信号的瞬时频率进行估计。传统的线性STFT方法在非线性系统中的应用效果较差,因为它假设信号的频率是恒定的,无法准确地捕捉到频率的变化。
非线性STFT通过引入非线性变换,可以更好地适应非线性系统中信号频率的变化。常用的非线性变换方法包括Wigner-Ville分布、Cohen类分布和S-method等。这些方法可以通过对信号进行时频分析,得到信号在时间和频率上的局部特征,从而实现对信号瞬时频率的估计。
非线性STFT在瞬时频率估计中的应用可以帮助我们更好地理解非线性系统中信号的特性。例如,在声音信号处理中,非线性STFT可以用于分析声音的共振特性和谐波结构,从而实现声音的合成和变换。在振动信号分析中,非线性STFT可以用于检测和诊断机械故障,通过分析信号的瞬时频率变化来判断机械系统的工作状态。
总之,非线性STFT在瞬时频率估计中的应用可以帮助我们更好地理解非线性系统中信号的特性,从而实现对信号的分析和处理。
📚2 运行结果
2.1 算例1
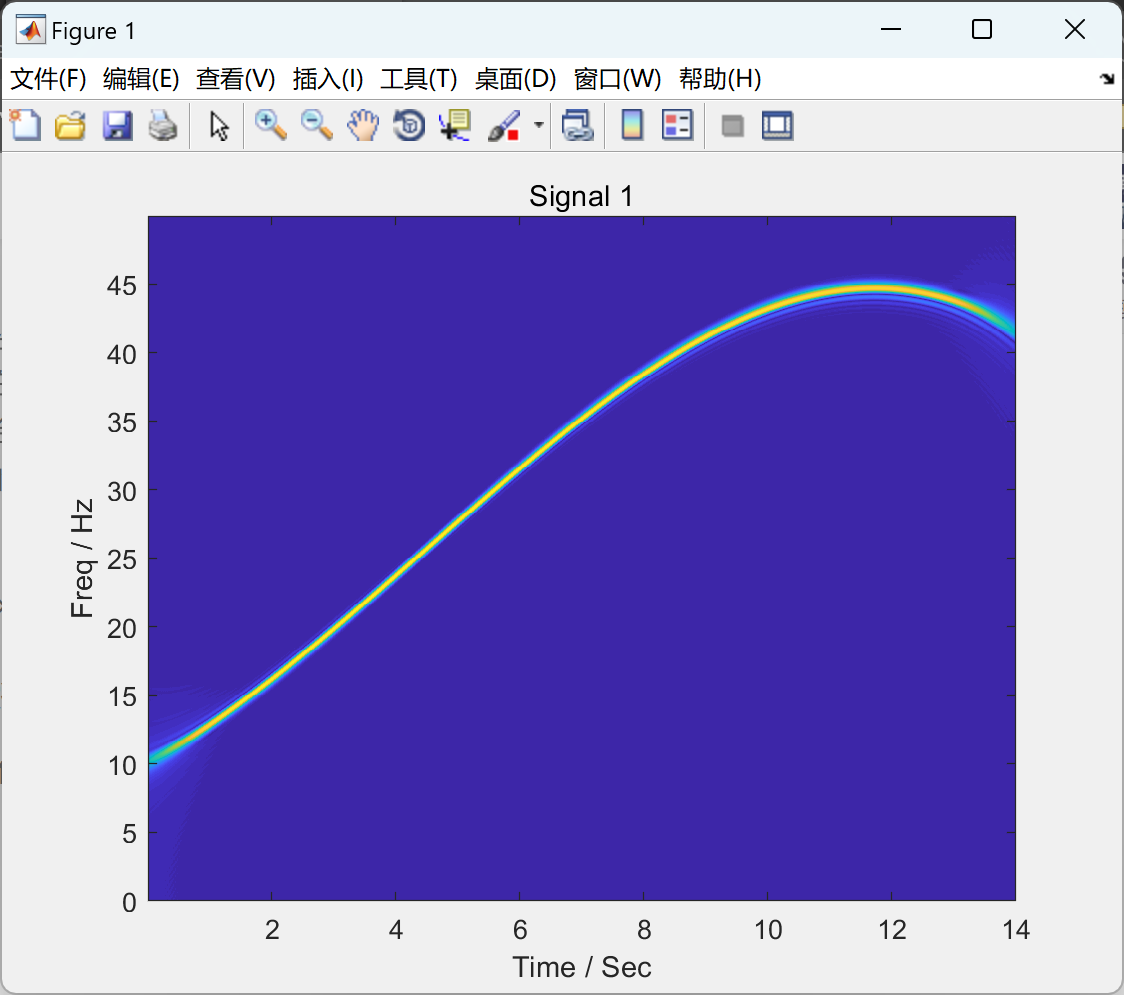
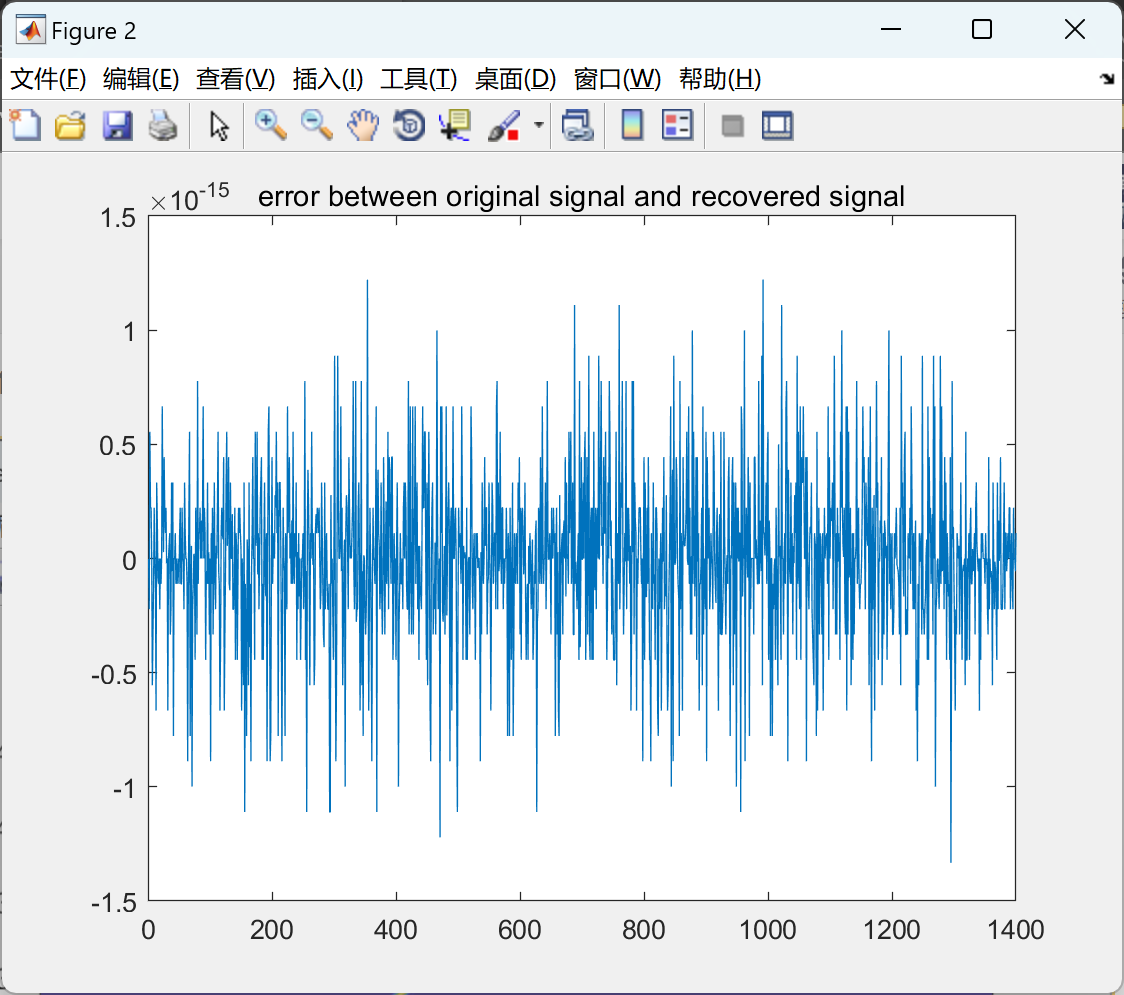
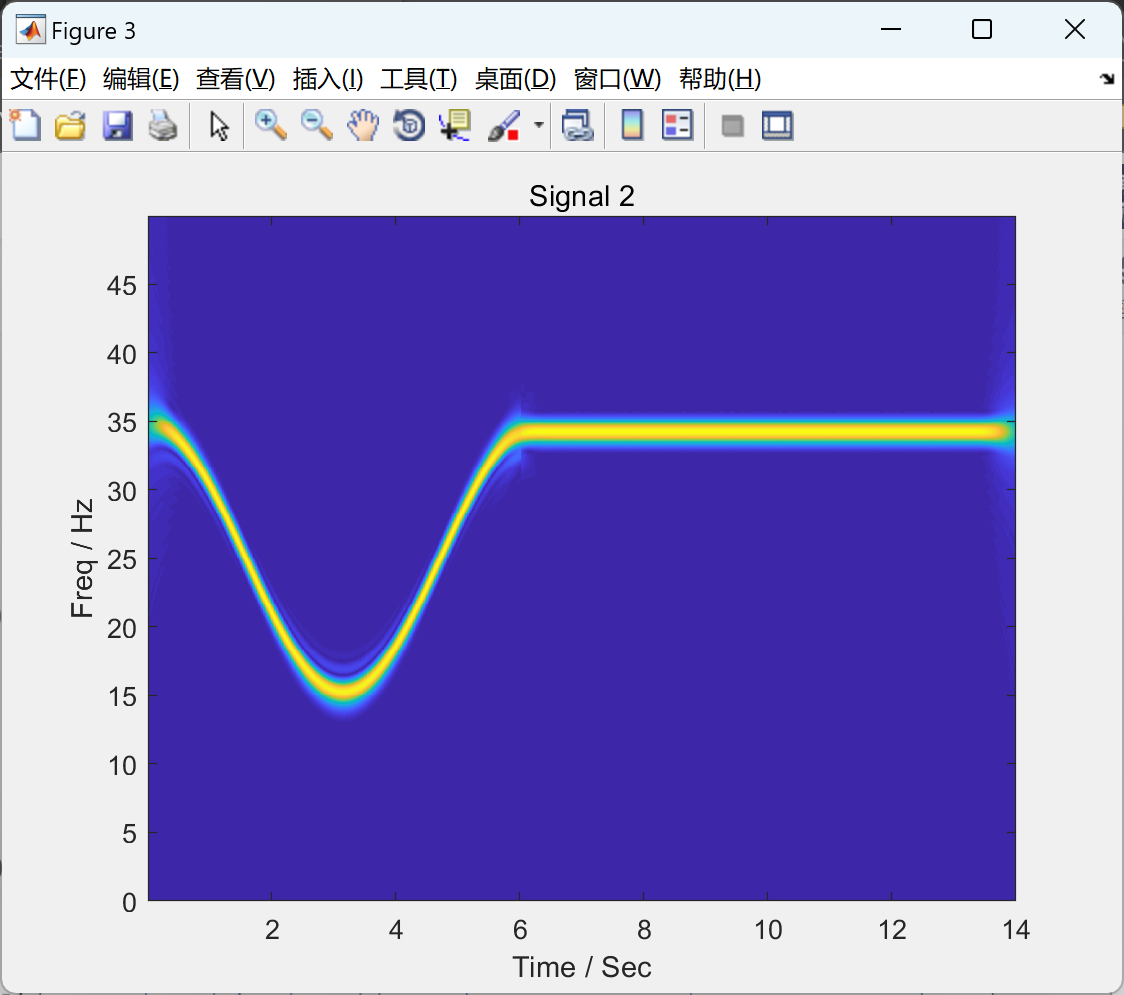

2.2 算例2
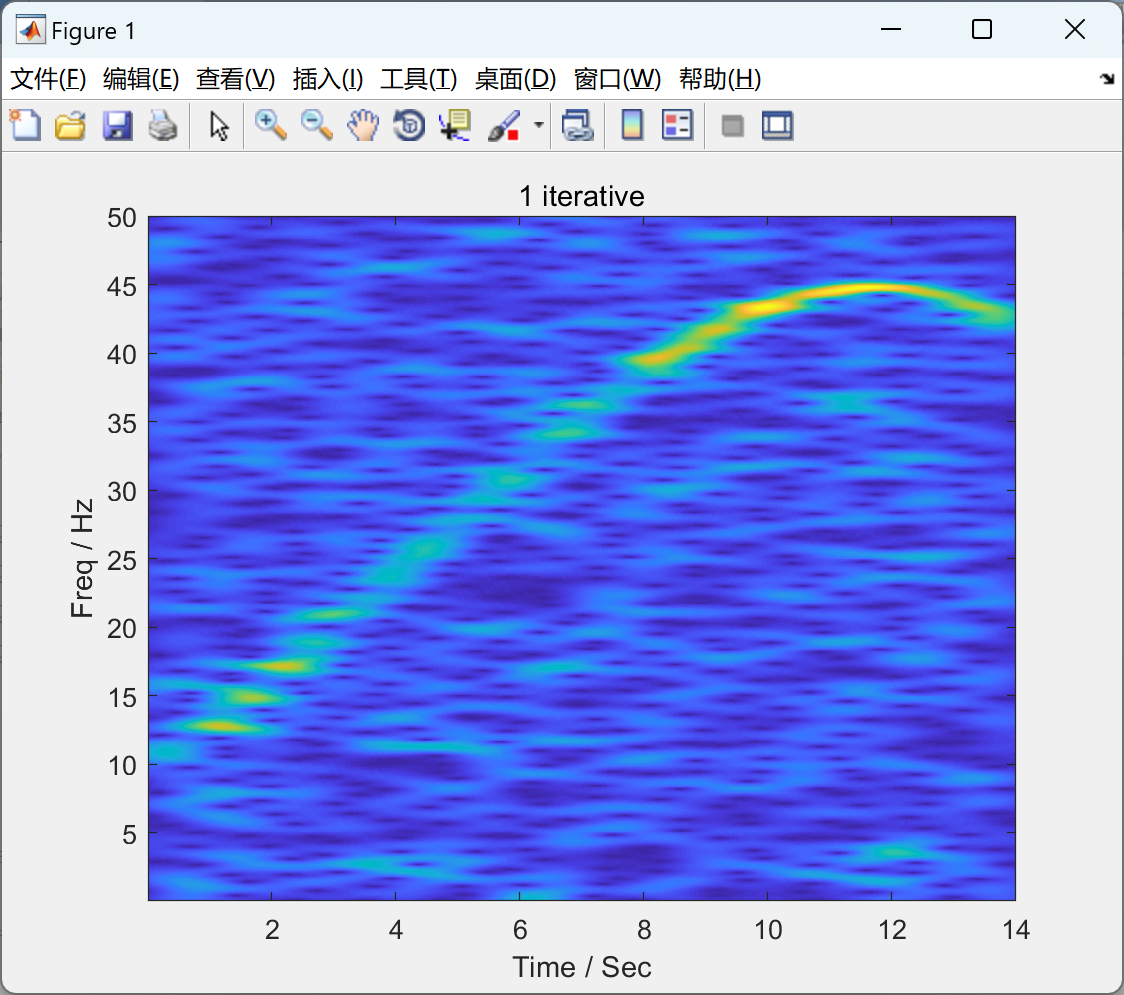
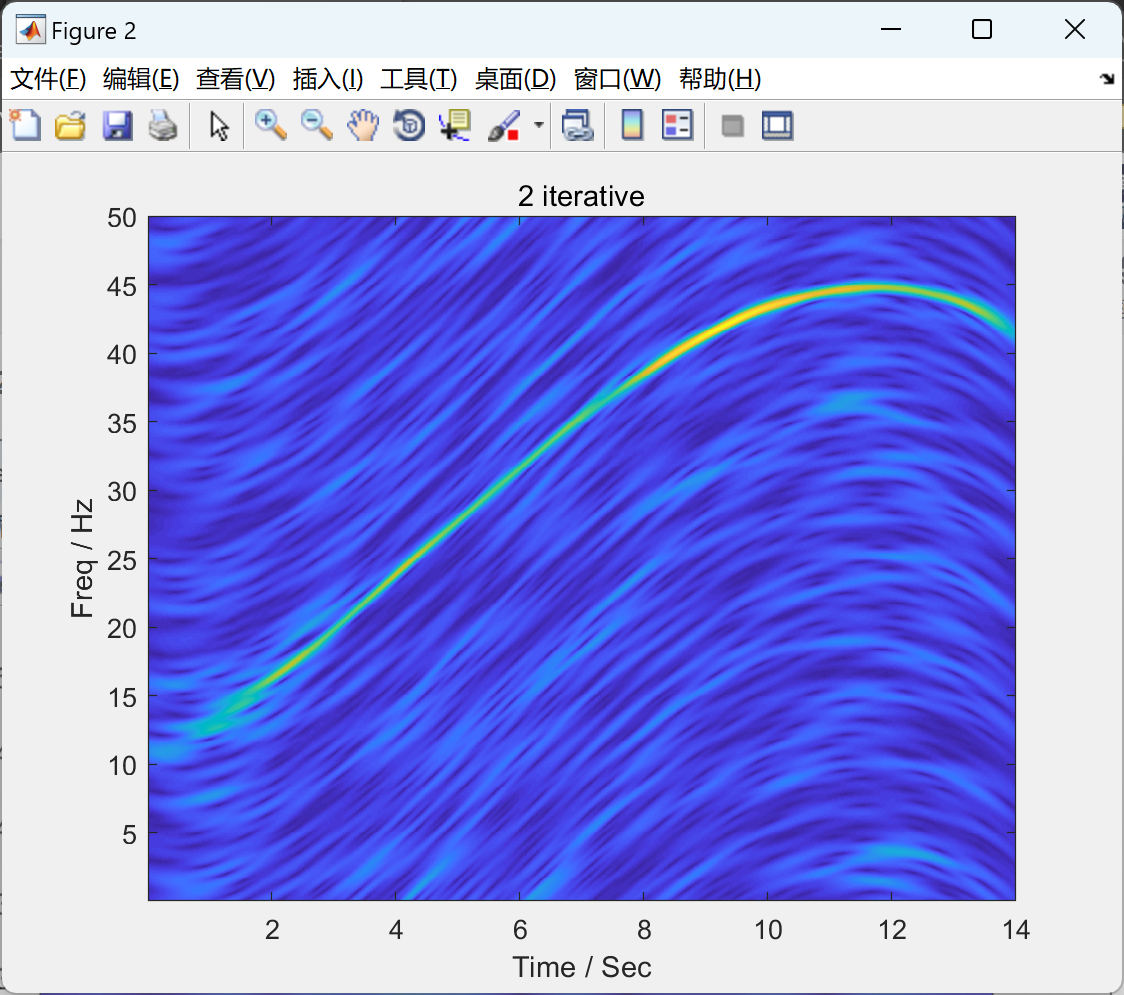
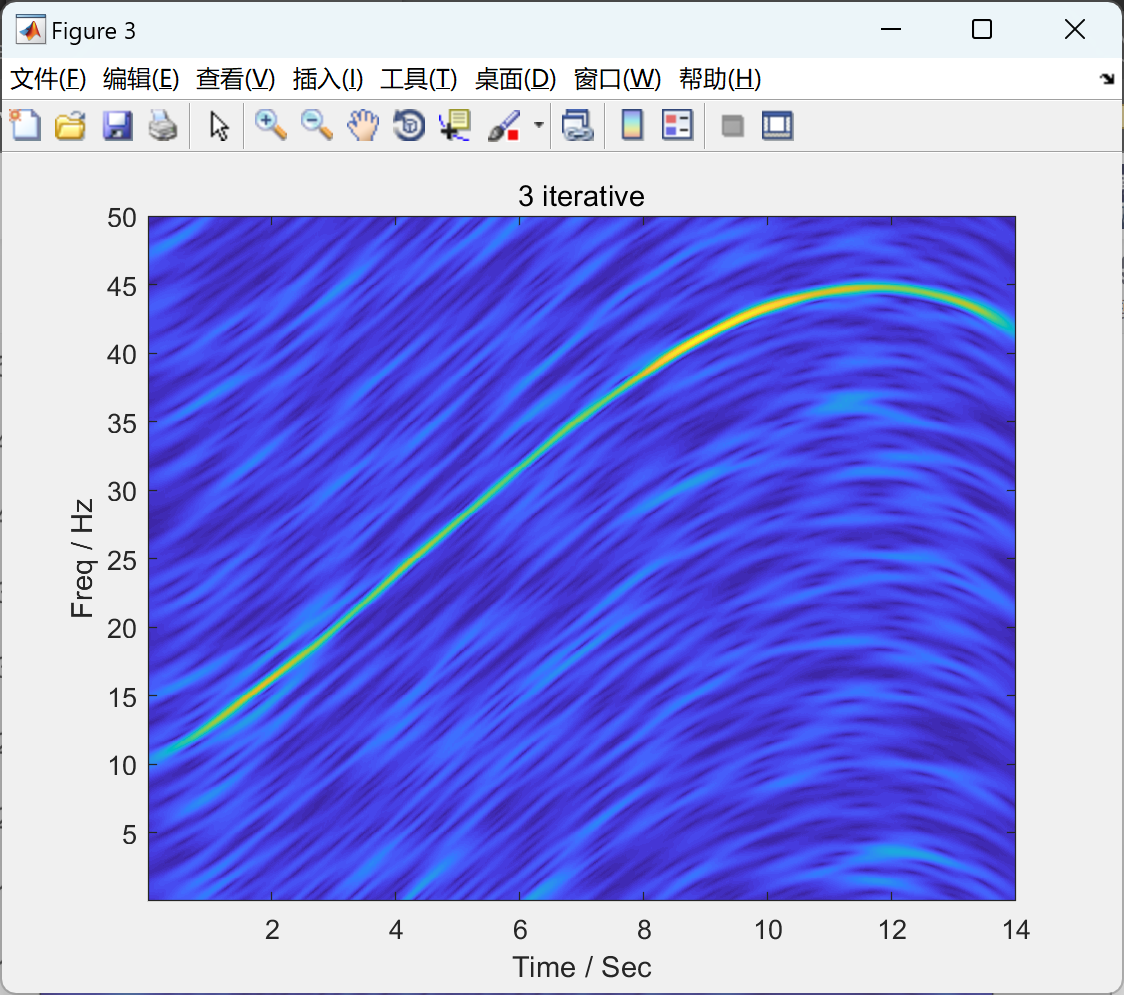
NLSTFT子函数代码:
function tfr = NLSTFT(x,c,fs,hlength);
% Non-linear Short time Fourier transform.
% x : Signal.
% c : First order derivative of signal IF.
% fs : Sample Frequency .
% hlength: Length of window function.
% tfr : Time-Frequency Representation.
%
% This program is free software; you can redistribute it and/or modify
% it according to your requirement.
[xrow,xcol] = size(x);
if (nargin < 3),
error('At least 3 parameter is required');
end;
Siglength=xrow;
if (nargin < 4),
hlength=floor(Siglength/4);
end;
hlength=hlength+1-rem(hlength,2);
h = tftb_window(hlength);
%t=1:xrow;
%[trow,tcol] = size(t);
[hrow,hcol]=size(h); Lh=(hrow-1)/2;
h=h/norm(h);
if (xcol~=1),
error('X must have one column');
end;
N=xrow;
t=1:xrow;
[trow,tcol] = size(t);
tt=(1:N)/fs;
tfr= zeros (N,tcol) ;
for icol=1:tcol,
ti= t(icol); tau=-min([round(N/2)-1,Lh,ti-1]):min([round(N/2)-1,Lh,xrow-ti]);
indices= rem(N+tau,N)+1;
rSig = x(ti+tau,1);
%rSig = Hilbert(real(rSig));
a=Lh+1+tau;
tfr(indices,icol)=rSig.*conj(h(Lh+1+tau)).*exp(j * 2.0 * pi * (c(icol)/2) * (tt(ti+tau)-tt(icol)).^2)';
end;
tfr=fft(tfr);
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]YuGang. Shandong University A Non-linear STFT With Application to Estimation of Instantaneous Frequency.
🌈4 Matlab代码实现
相关文章:

【时频分析,非线性中频】非线性STFT在瞬时频率估计中的应用(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
)
MTK平台关机流程和原因(二)
(1)ShutdownThread 从上一篇可以看到,最终会调用此类的shutdown以及reboot等函数,我们来看一下这些函数的实现。 (A)被调用函数 //frameworks/base/services/core/java/com/android/server/power/Shutdo…...

【Python】pyqt6入门到入土系列,非常详细...
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 一、什么是PyQt6? 简单介绍一下PyQt6 1、基础简介 PyQt6 Digia 公司的 Qt 程序的 Python 中间件。Qt库是最强大的GUI库之一。 PyQt6的官网:www.riverbankcomputing.co.uk/news。 PyQt6是由Riverbank Co…...

TCP socket编程
一、服务端代码 #encoding utf -8 #导入socket库 from socket import * #等待客户端来连接,主机地址为0.0.0.0表示绑定本机所有网络接口ip地址 IP 0.0.0.0 #端口号 PORT 50000 #定义一次从socket缓存区最多读入512个字节数据 BUFLEN 512 #实例化一个socket编程…...

HTTP——一、了解Web及网络基础
HTTP 一、使用HTTP协议访问Web二、HTTP的诞生1、为知识共享而规划Web2、Web成长时代3、驻足不前的HTTP 三、网络基础TCP/IP1、TCP/IP协议族2、TCP/IP的分层管理3、TCP/IP 通信传输流 四、与HTTP关系密切的协议:IP、TCP和DNS1、负责传输的 IP 协议2、确保可靠性的TCP…...

[论文笔记] chatgpt系列 2.6 DeepSpeed-chat 数据集
一、FT数据集 & Reward model数据集 Deepspeed-chat 源代码的数据集: Dahoas/rm-static: 这是一个用于强化学习的静态环境数据集,包含了一个机器人在一个固定环境中的运动轨迹。该数据集旨在用于评估强化学习算法在静态环境下的表现。 Dahoas/full-hh-rlhf: 这是一个用于…...
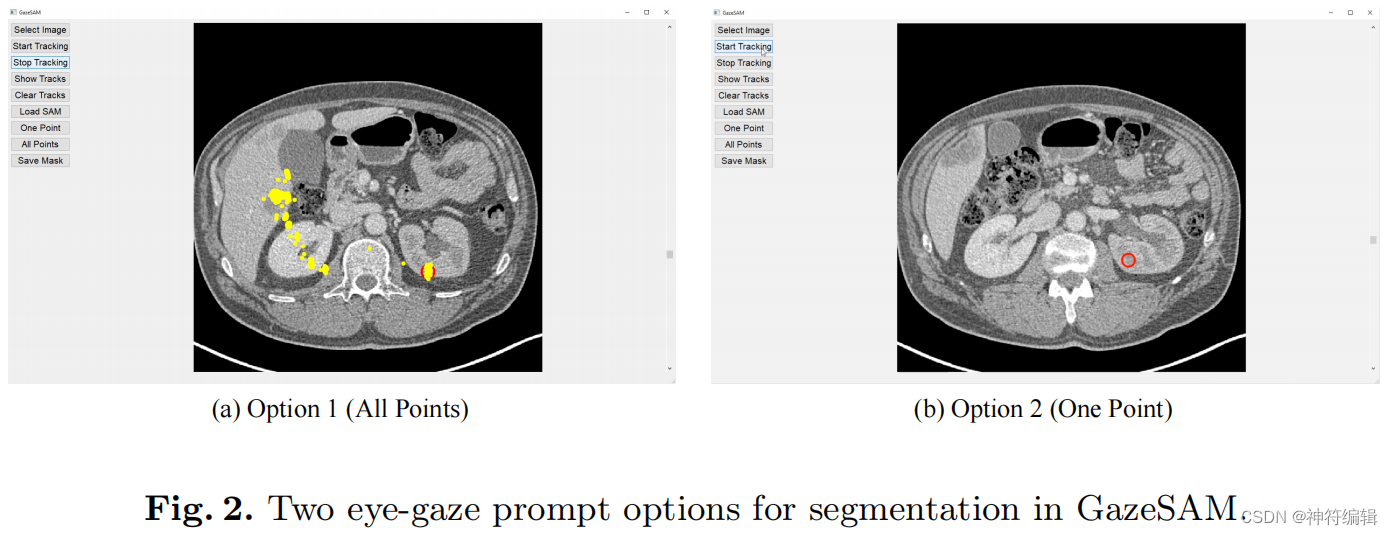
探究SAM和眼球追踪技术在自动医学图像分割的应用(2023+GazeSAM: What You See is What You Segment)
摘要: 本研究探讨眼动追踪技术与SAM的潜力,以设计一个协同的人机交互系统,自动化医学图像分割。提出了GazeSAM系统,使放射科医生能够在图像诊断过程中通过简单地查看感兴趣的区域来收集分割掩模。该系统跟踪放射科医生的眼球运动…...
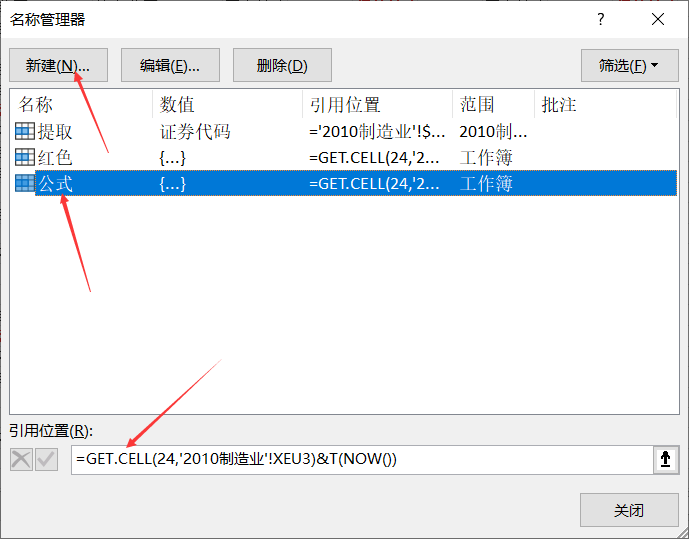
excle中的条件求和SUMIF
问题:将每一行中红色文字的前一个值累计求和到境外总数这一列 使用的公式 自制单元格的格式计算公式:ctrlf3打开格式管理,创建如下公式,其中24是表示获取文字颜色 由于sumif只能直接与第二参数条件比较,所以先使用IF(公…...

python-网络爬虫.Request
Request python中requests库使用方法详解: 一简介: Requests 是Python语言编写,基于urllib, 采用Apache2 Licensed开源协议的 HTTP 库。 与urllib相比,Requests更加方便,处理URL资源特别流畅。 可以节约我…...
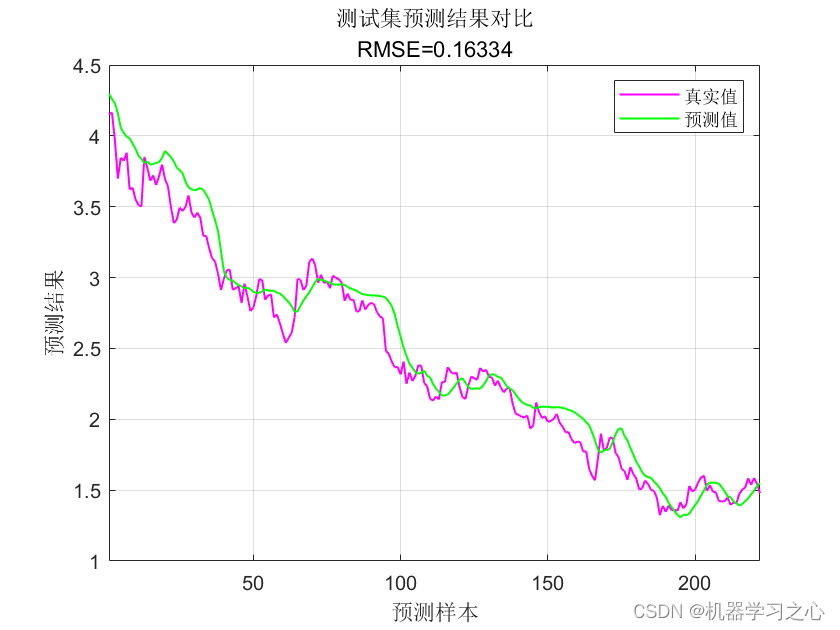
时序预测 | MATLAB实现GRNN广义回归神经网络时间序列预测(多指标,多图)
时序预测 | MATLAB实现GRNN广义回归神经网络时间序列预测(多指标,多图) 目录 时序预测 | MATLAB实现GRNN广义回归神经网络时间序列预测(多指标,多图)效果一览基本介绍程序设计参考资料效果一览 基本介绍 1.MATLAB实现GRNN广义回归神经网络时间序列预测(完整源码和数据) …...
如何看待低级爬虫与高级爬虫?
爬虫之所以分为高级和低级,主要是基于其功能、复杂性和灵活性的差异。根据我总结大概有下面几点原因: 功能和复杂性:高级爬虫通常提供更多功能和扩展性,包括处理复杂页面结构、模拟用户操作、解析和清洗数据等。它们解决了开发者…...

3.分支与循环
一、分支结构 1.概念 一个 CPP 程序默认是按照代码书写顺序,从上到下依次执行下来的。但是,有时我们需要选择性的执行某些语句,来实现更加复杂的逻辑,这时候就需要分支结构语句的功能来实现。选择合适的分支语句可以显著提高程序…...
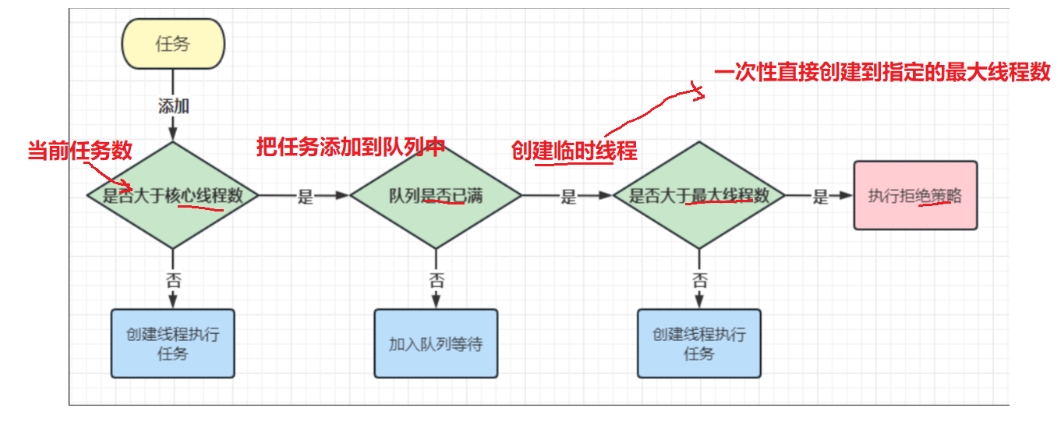
面试之多线程案例(四)
1.单例模式 单例模式是指在内存中只会创建且仅创建一次对象的设计模式。在程序中多次使用同一个对象且作用相同时,为了防止频繁地创建对象使得内存飙升,单例模式可以让程序仅在内存中创建一个对象,让所有需要调用的地方都共享这一单例对象。…...
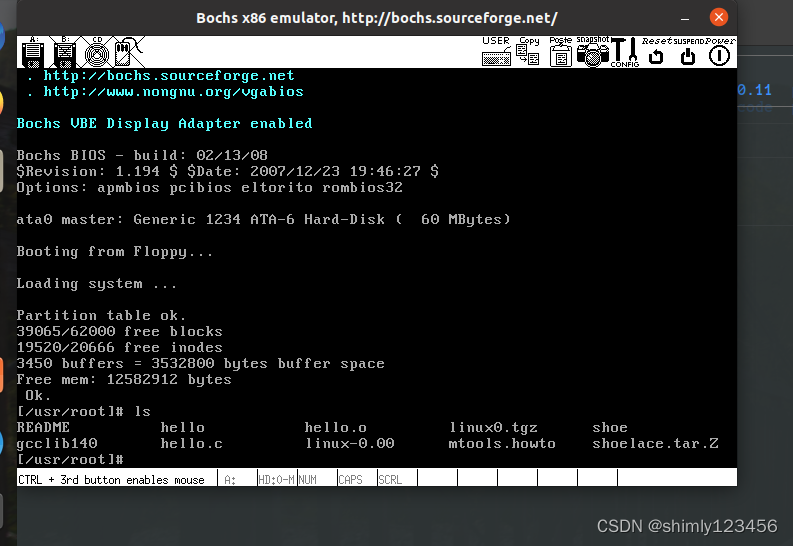
抄写Linux源码(Day1:获取并运行 Linux0.11)
Day1:获取并运行 Linux0.11 参考资料:https://zhuanlan.zhihu.com/p/438577225 这是我参考的一个别人写的 Linux0.11 解读:https://github.com/dibingfa/flash-linux0.11-talk 我获取 Linux-0.11 源码的链接:https://github.com/…...
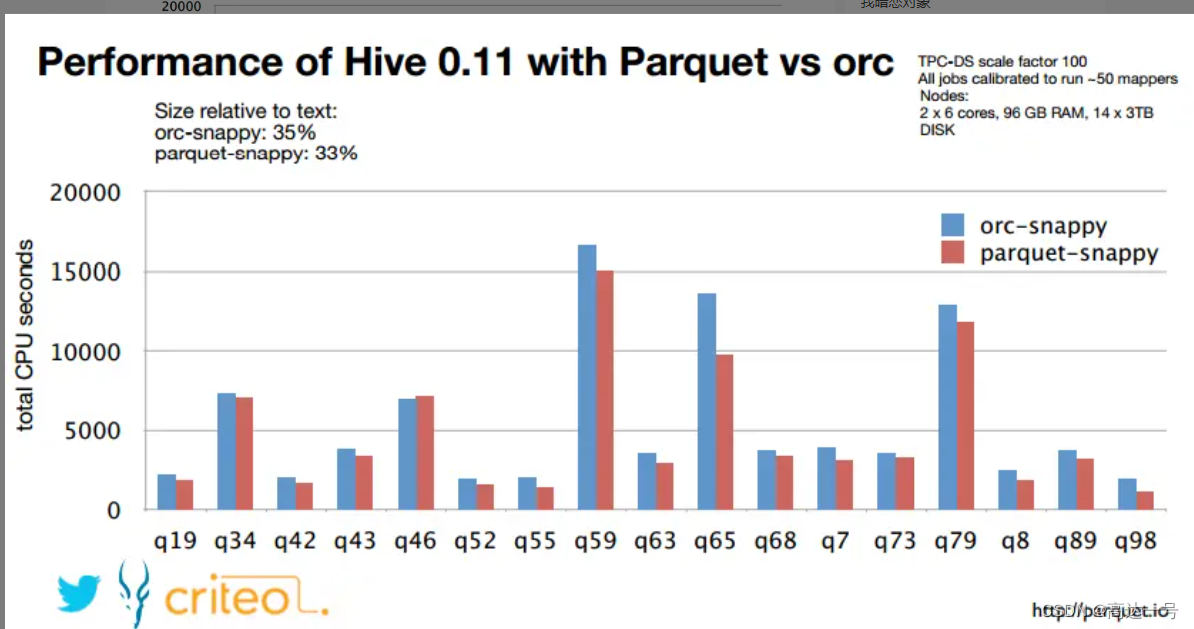
大数据_Hadoop_Parquet数据格式详解
之前有面试官问到了parquet的数据格式,下面对这种格式做一个详细的解读。 参考链接 : 列存储格式Parquet浅析 - 简书 Parquet 文件结构与优势_parquet文件_KK架构的博客-CSDN博客 Parquet文件格式解析_parquet.block.size_davidfantasy的博客-CSDN博…...

Docker的安装和部署
目录 一、Docker的安装部署 (1)关闭防火墙 (2)关闭selinux (3)安装docker引擎 (4)启动docker (5)设置docker自启动 (6)测试doc…...

FPGA项目实现:秒表设计
文章目录 项目要求项目设计 项目要求 设计一个时钟秒表,共六个数码管,前两位显示分钟,中间两位显示时间秒,后两位显示毫秒的高两位,可以通过按键来开始、暂停以及重新开始秒表的计数。 项目设计 为完成此项目共设计…...
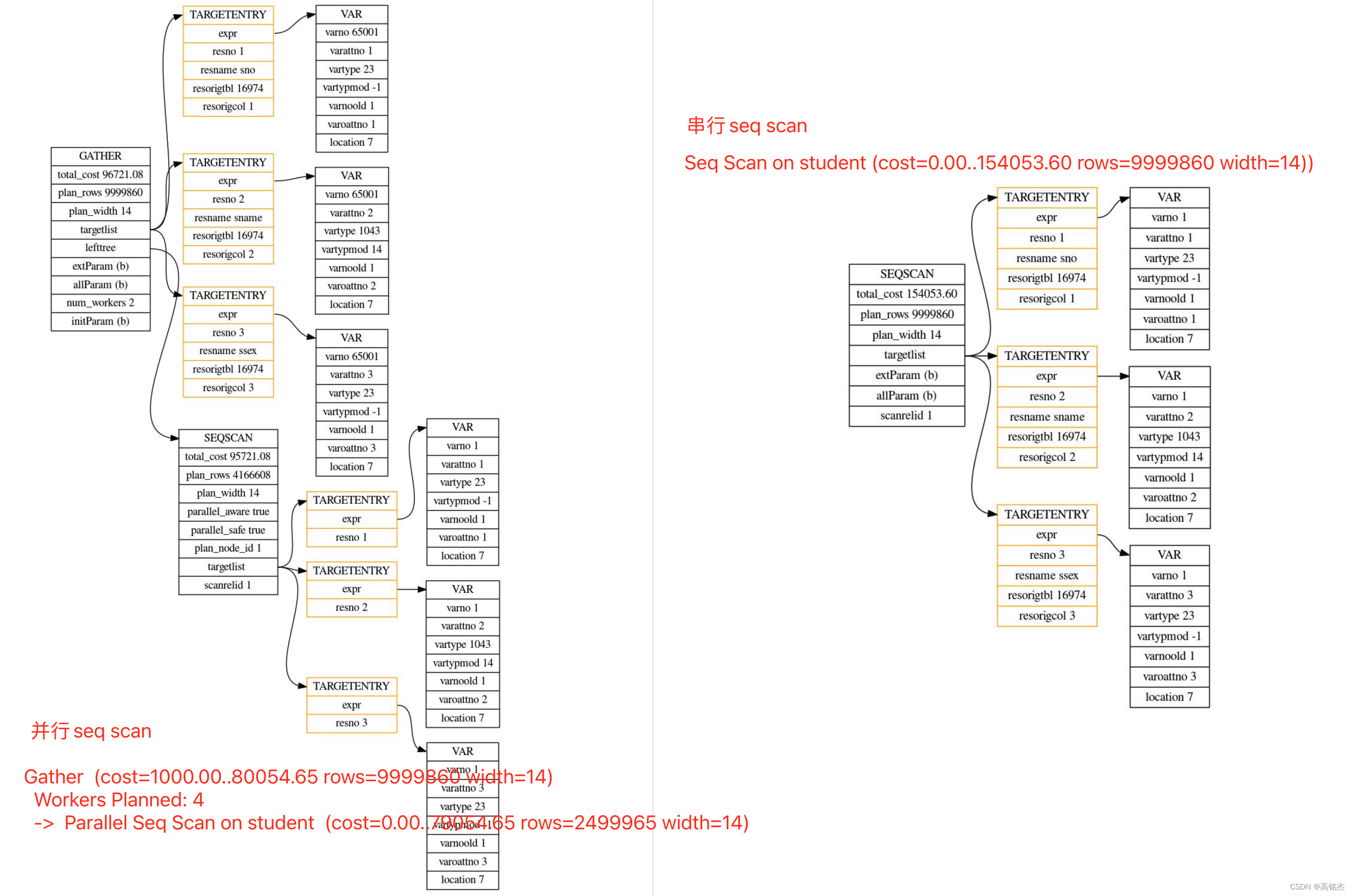
Postgresql源码(109)并行框架实例与分析
1 PostgreSQL并行参数 系统参数 系统总worker限制:max_worker_processes 默认8 系统总并发限制:max_parallel_workers 默认8 单Query限制:max_parallel_workers_per_gather 默认2 表参数限制:parallel_workers alter table tbl …...

ES派生类的prototype方法中,不能访问super的解决方案
1 下面的B.prototype.compile方法中,无法访问super class A {compile() {console.log(A)} }class B extends A {compile() {super.compile()console.log(B)} }B.prototype.compile function() {super.compile() // 报错,不可以在此处使用superconsole.…...

使用adb通过电脑给安卓设备安装apk文件
最近碰到要在开发板上安装软件的问题,由于是开发板上的安卓系统没有解析apk文件的工具,所以无法通过直接打开apk文件来安装软件。因此查询各种资料后发现可以使用adb工具,这样一来可以在电脑上给安卓设备安装软件。 ADB 就是连接 Android 手…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

