杭电多校2023“钉耙编程”中国大学生算法设计超级联赛(5)
| 1006 | Touhou Red Red Blue |
dp
设状态方程为前i个数中,当前第一个包里面的是0/1/2/3状态,第二个包里面是0/1/2/3状态
0代表着还没有颜色,1代表R,2代表G,3代笔B颜色
初始状态都没选择颜色所以都是状态0
没选择颜色只能从后面的字符里面选
细想操作一 a b两个包清空,然后a选择任意颜色,b从后面的选,
换句话说就是a的颜色要取决于后面的颜色,所以不如直接让b变成任意颜色,a状态变成0
后面选择的字符放到a,其实是等效的,且这样遍历
else f[i][b][c]=max(f[i][b][c],f[i-1][a][b]);
我不用另外判断这个条件
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10,mod=998244353;typedef long long LL;
typedef pair<int, int> PII;int n;
int f[N][5][5];
int get(char c){if(c=='R') return 1;else if(c=='G') return 2;else return 3;
}void solve(){memset(f,-0x3f,sizeof(f));string s;cin>>s;n=s.size();s="?"+s;f[0][0][0]=0;for(int i=1;i<=n;i++){int c=get(s[i]);for(int a=0;a<=3;a++){for(int b=0;b<=3;b++){f[i][a][b]=f[i-1][a][b];}}for(int a=0;a<=3;a++){for(int b=0;b<=3;b++){if(a==b&&b==c){for(int d=1;d<=3;d++){f[i][0][d]=max(f[i][0][d],f[i-1][a][b]+1);}}else if(a&&b&&c&&a!=b&&a!=c&&b!=c){for(int d=1;d<=3;d++){for(int e=1;e<=3;e++){f[i][d][e]=max(f[i][d][e],f[i-1][a][b]);}}}else f[i][b][c]=max(f[i][b][c],f[i-1][a][b]);}}}int res=0;for(int a=0;a<=3;a++){for(int b=0;b<=3;b++)res=max(res,f[n][a][b]);}cout<<res<<"\n";
}
signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}| 1012 | Counting Stars |
首先统计度数
k星图可以由
k+1星图选择去掉其中1条边里面的其中一条变成
k+2星图选择去掉其中2条边里面的其中两条变成
...
所以直接统计度数即可
然后每个点暴力枚举2到d[i]的k星图增加个数即可
复杂度是n+m
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10,mod=1e9+7;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
int n,m,k;
int fact[N],infact[N];
int qmi(int a, int k, int p) // 求a^k mod p
{int res = 1 % p;while (k){if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}void init(){fact[0] = infact[0] = 1;for (int i = 1; i < N; i ++ ){fact[i] = (LL)fact[i - 1] * i % mod;infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;}
}
int C(int a,int b){if(b>a) return 0;return ((LL)fact[a] * infact[b] % mod * infact[a - b] % mod);
}
void solve(){int n,m;cin>>n>>m;vector<int> d(n+10,0),ans(n+10,0);for(int i=1;i<=m;i++){int a,b;cin>>a>>b;d[a]++,d[b]++;}for(int i=1;i<=n;i++){long long tmp=d[i]*(d[i]-1)/2%mod;for(int j=2;j<=d[i];j++){ans[j]=(ans[j]+C(d[i],j))%mod;}} long long res=0;for(int i=2;i<=n-1;i++)res^=ans[i];cout<<res<<"\n";
}signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;init();cin>>t;while(t--) solve();
}| 1007 | Expectation (Easy Version) |
直接枚举即可
当前i 贡献是i^m,概率是n场里面选择i场赢,赢i场的概率*输(n-i)场的概率
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;int n;
int a[N],b[N];
int fact[N],infact[N];
int qmi(int a, int k, int p) // 求a^k mod p
{int res = 1 % p;while (k){if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}void init(){fact[0] = infact[0] = 1;for (int i = 1; i < N; i ++ ){fact[i] = (LL)fact[i - 1] * i % mod;infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;}
}
int C(int a,int b){if(b>a) return 0;return ((LL)fact[a] * infact[b] % mod * infact[a - b] % mod);
}
int gcd(int a, int b) // 欧几里得算法
{return b ? gcd(b, a % b) : a;
}
void solve(){int n,m,x,y;cin>>n>>m>>x>>y;int win=x*qmi(y,mod-2,mod)%mod;int sum=0,ans=0;a[0]=b[0]=1;for(int i=1;i<=n;i++) a[i]=a[i-1]*win%mod;for(int i=1;i<=n;i++) b[i]=b[i-1]*(1-win+mod)%mod;for(int i=1;i<=n;i++){sum=(sum+qmi(i,m,mod))%mod;int res=C(n,i)*a[i]%mod*b[n-i]%mod*sum%mod;ans=(ans+res)%mod;}cout<<(ans+mod)%mod<<"\n";
}
signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;init();cin>>t;while(t--) solve();
}| 1003 | String Magic (Easy Version) |
对于每个下标 用合法的起点减去不合法的终点就是答案了,注释在代码里
要用到马拉车算法,求出f[ ]数组就是以i为中心的回文字符串的长度
每个字符串对应一个
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+10,mod=998244353;typedef long long LL;
typedef pair<int, int> PII;
int n;
char ss[N];
int f[N];
int sum[N];
vector<int> V[N];
int tr[N];
int lowbit(int x)
{return x & -x;
}void add(int x, int c) // 位置x加c
{while(x){tr[x]+=c;x-=lowbit(x);}
}int query(int x) // 返回前x个数的和
{int res = 0;while(x<=n+n){res+=tr[x];x+=lowbit(x);}return res;
}void solve(){int ans=0;string s;cin>>s;n=s.size();s="?"+s;ss[0]='?';ss[n+n+2]='^';for(int i=1;i<=n;++i){ss[i+i-1]='*';ss[i+i]=s[i];ss[i+i+1]='*';}for(int i=1;i<=n+n;++i) V[i].clear(),tr[i]=0,f[i]=0;int mr=0,mid=0;for(int i=1;ss[i]!='^';i++){if(i<mr) f[i]=min(mr-i,f[2*mid-i]);else f[i]=1;while(ss[i+f[i]]==ss[i-f[i]]) f[i]++;if(f[i]+i>mr){mr=f[i]+i;mid=i;}}for(int i=1;i<=n+n;i++) f[i]--;//f[i]是求每个点为中心的最长回文串的长度for(int i=3;i<=n+n;++i){if(i%2==0) continue;V[i-1].push_back(i);//有个性质*号的位置如果长度不是1,那么他对应的字符串长度一定是偶数//不是*号的字母回文字符一定包含*号 *a* 所以这是合法对数的起点V[i-(f[i]+1)/2-1].push_back(-i);//i-(f[i]+1)/2-1 的点就已经不在i的回文范围内了}for(int i=1;i<=n+n;++i){add(i+f[i],1);//当前i能扩展到右边的端点位置for(auto v:V[i]){if(v>0) ans+=query(v);else ans-=query(-v);//相当于起点减去终点}}cout<<ans<<"\n";
}
signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}相关文章:
)
杭电多校2023“钉耙编程”中国大学生算法设计超级联赛(5)
1006Touhou Red Red Blue dp 设状态方程为前i个数中,当前第一个包里面的是0/1/2/3状态,第二个包里面是0/1/2/3状态 0代表着还没有颜色,1代表R,2代表G,3代笔B颜色 初始状态都没选择颜色所以都是状态0 没选择颜色只…...
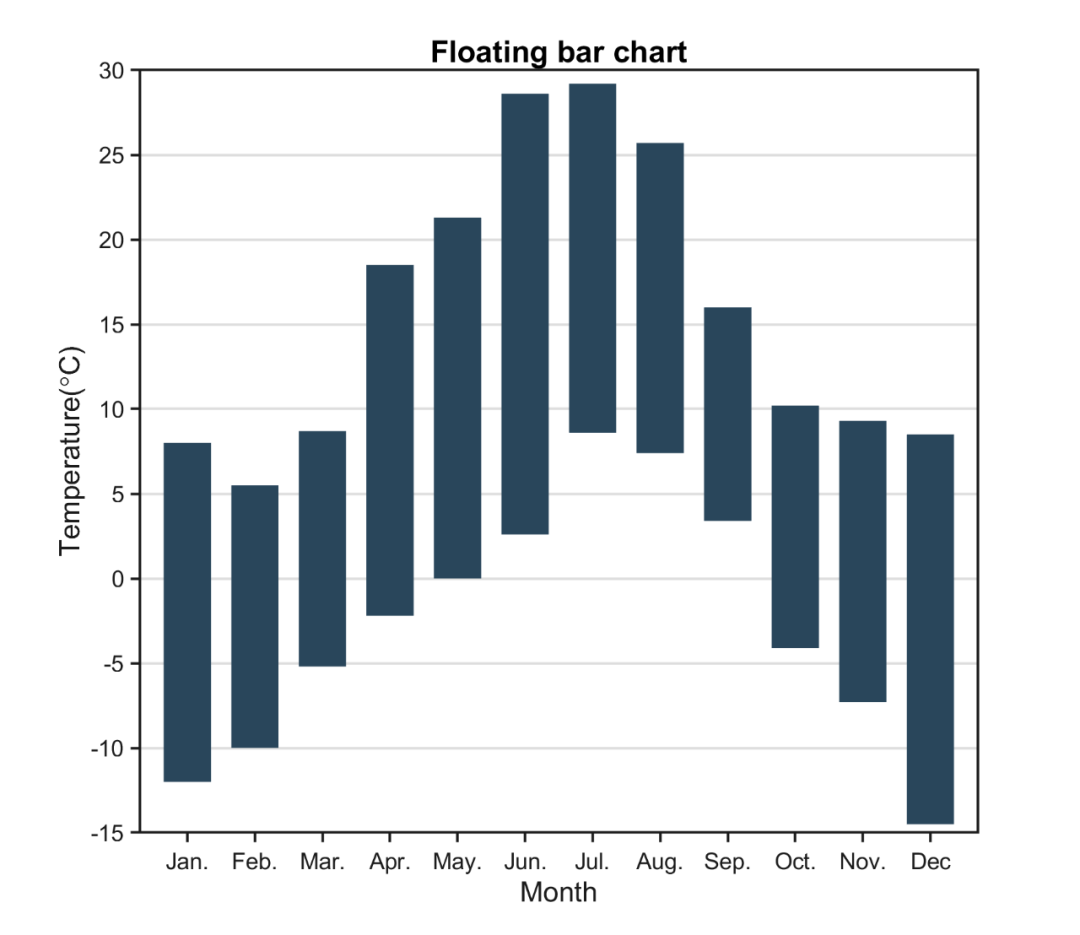
Matlab进阶绘图第24期—悬浮柱状图
悬浮柱状图是一种特殊的柱状图。 与常规柱状图相比,悬浮柱状图可以通过悬浮的矩形展示最小值到最大值的范围(或其他范围表达),因此在多个领域得到应用。 本文使用自己制作的Floatingbar小工具进行悬浮柱状图的绘制,先…...

【题解】链表中倒数最后k个结点、删除链表的倒数第n个节点
文章目录 链表中倒数最后k个结点删除链表的倒数第n个节点 链表中倒数最后k个结点 题目链接:链表中倒数最后k个结点 解题思路1:先找长度再找k对应的节点 首先遍历一遍链表找到链表的长度n 然后比较长度和k的大小关系,如果比k小,…...

网络安全大厂面试题
自我介绍 有没有挖过src? 平时web渗透怎么学的,有实战吗?有过成功发现漏洞的经历吗? 做web渗透时接触过哪些工具 xxe漏洞是什么?ssrf是什么? 打ctf的时候负责什么方向的题 为什么要搞信息安全,对…...

7.事件类型
7.1鼠标事件 案例-轮播图点击切换 需求:当点击左右的按钮,可以切换轮播图 分析: ①右侧按钮点击,变量,如果大于等于8,则复原0 ②左侧按钮点击,变量–,如果小于0,则复原最后一张 ③鼠…...

ts中声明引入未使用的报错——解决方案
在编写ts项目的时候,经常会出现如下报错: 导入声明中的所有导入都未使用 这是因为导入的模块暂时没有使用,ts给的一个提示信息 解决方案: 在ts.config.json中 把noUnusedLocals 设置为false即可 {"compilerOptions"…...
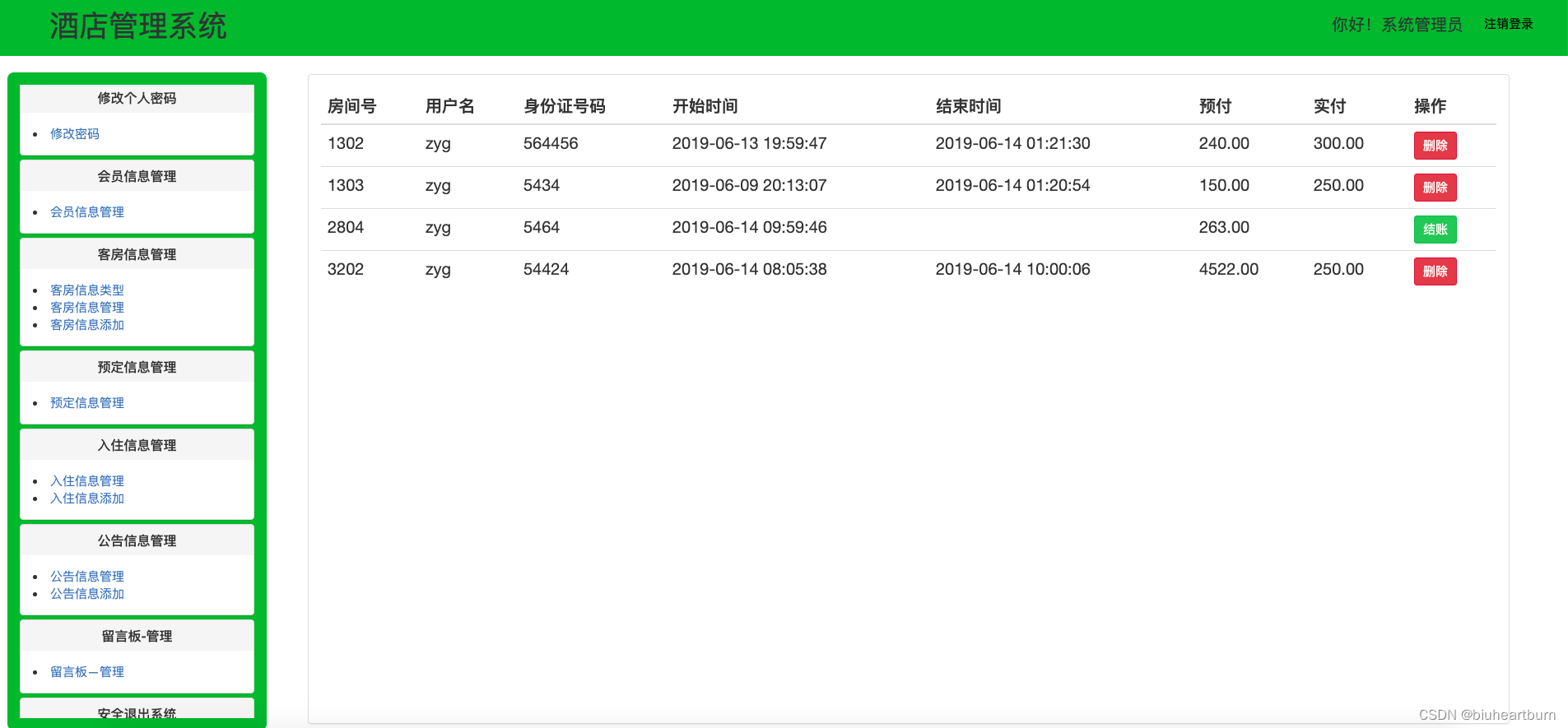
集团MySQL的酒店管理系统
酒店管理系统 概述 基于Spring Spring MVC MyBatis的酒店管理系统,主要实现酒店客房的预定、入住以及结账等功能。使用Maven进行包管理。 用户端主要功能包括: 登录注册、客房预订、客房评论(编写评论和查看评论) 后台管理主要…...
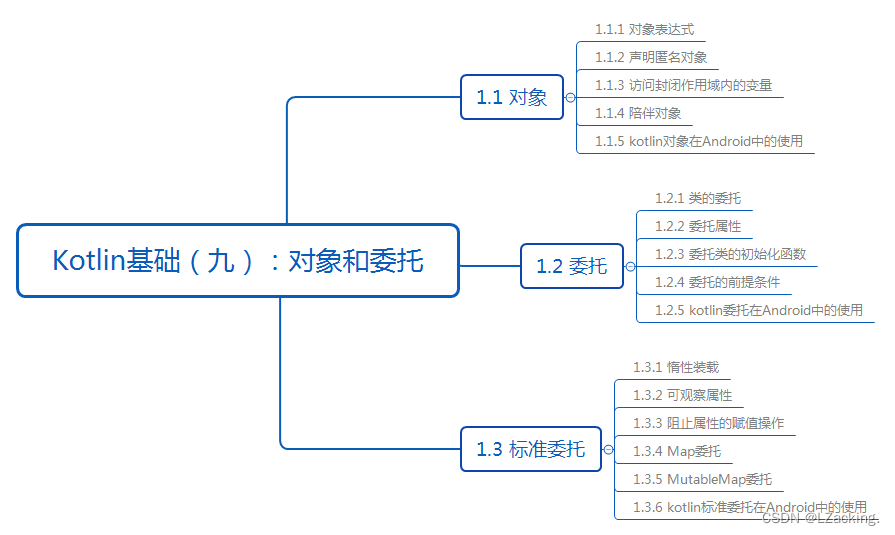
Kotlin基础(九):对象和委托
前言 本文主要讲解kotlin对象和委托。 Kotlin文章列表 Kotlin文章列表: 点击此处跳转查看 目录 1.1 对象 在Kotlin中,对象(Object)是一个具有特殊用途的单例实例。它是一种创建单个实例的方式,确保在整个应用程序中只存在一个特…...

八大排序算法--希尔排序(动图理解)
目录 希尔排序 概念 算法思路 动画演示 代码如下 复杂度分析 时间复杂度测试 运行结果 完整代码 创作不易,如果本篇博客对您有一定的帮助,大家记得留言点赞哦。 希尔排序 概念 希尔排序是插入排序的一种,是对直接插入排序的优化。其…...
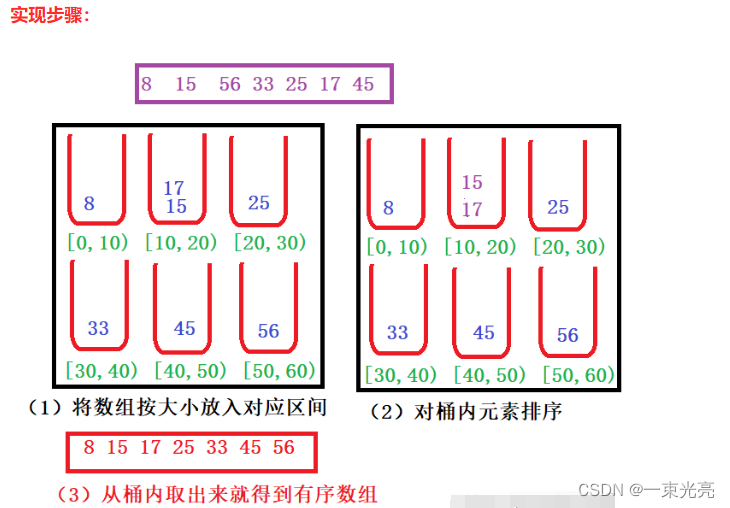
数据结构之常见排序算法
文章目录 1.排序概念2.10种排序比较3.排序算法3.1直接插入排序(元素越有序,越高效)3.2希尔排序序( 缩小增量排序 )3.3直接选择排序3.5堆排序3.6冒泡排序3.8快速排序 递归实现(无序使用最好)3.8.1挖坑法 (建…...
Java版企业电子招标采购系统源代码Spring Boot + 二次开发 + 前后端分离 构建企业电子招采平台之立项流程图
项目说明 随着公司的快速发展,企业人员和经营规模不断壮大,公司对内部招采管理的提升提出了更高的要求。在企业里建立一个公平、公开、公正的采购环境,最大限度控制采购成本至关重要。符合国家电子招投标法律法规及相关规范,以及审…...

2.2 模型与材质基础
一、渲染管线与模型基础 1. 渲染管线 可编程阶段(蓝色区域): 1顶点着色器 2几何着色器 3片元着色器 2. 模型的实现原理 UV:在建模软件中,进行UV展开,UV会放在一个横向为U纵向为V,范围࿰…...

什么是Docker
一 、什么是Docker 1.1 简介 Docker 使用 Google 公司推出的 Go 语言 (opens new window)进行开发实现,基于 Linux 内核的 cgroup (opens new window),namespace (opens new window),以及 OverlayFS (opens new window)类的 Union FS (open…...

1109. 航班预订统计
这里有 n 个航班,它们分别从 1 到 n 进行编号。 有一份航班预订表 bookings ,表中第 i 条预订记录 bookings[i] [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti (包含 firsti 和 lasti )的 每个航班 上预订了 seatsi 个座…...

[SQL挖掘机] - 窗口函数 - 合计: rollup
介绍: rollup 是一种用于在 sql 查询中生成聚合数据的特殊操作。它可以创建包含子总计和总计的结果集,并可用于生成层次化报表或汇总数据。 rollup 操作在 group by 子句中使用,可以在查询结果中生成多级汇总数据。它会根据指定的列进行分组࿰…...

2022年全国硕士研究生入学统一考试管理类专业学位联考写作试题——解析版
四、写作:第56~57小题,共65分。其中论证有效性分析30分,论说文35分。 56.论证有效性分析:分析下述论证中存在的缺陷和漏洞,选择若干要点,写一篇600字左右的文章,对该论证的有效性进…...

元类在测试框架中的运用
元类在测试框架中的运用 书接上回 我们知道了元类的基本用法,也写了一个小demo,接下来我们就尝试运用进我们测试框架。 #一款无需编码且易用于二次开发的接口测试框架。 #我写的我写的我写的我写的 pip install mwj-apitest #这里面就用到了元类&…...

VBA快速交叉分段标记字符颜色
实例需求:A列中有不确定行数的数据,现在需要将数据按照每4位一组间隔标记颜色,如下图所示。 示例代码如下。 Sub Demo()Dim rngCell As RangeDim rngData As RangeDim i, res, intLenSet rngData Range("A1").CurrentRegionrngDa…...

根据Pytorch源码实现的 ResNet18
一,类模块定义: import torch import torch.nn as nn import torch.nn.functional as F from torch import Tensorclass ResBlock(nn.Module):def __init__(self, inchannel, outchannel, stride1) -> None:super(ResBlock, self).__init__()# 这里定义了残差块…...
药品管理系统servlet+jsp+sql医院药店仓库进销存java源代码mysql
本项目为前几天收费帮学妹做的一个项目,Java EE JSP项目,在工作环境中基本使用不到,但是很多学校把这个当作编程入门的项目来做,故分享出本项目供初学者参考。 一、项目描述 药品管理系统servletjspsql 系统有1权限:…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
