DSA之图(4):图的应用
文章目录
- 0 图的应用
- 1 生成树
- 1.1 无向图的生成树
- 1.2 最小生成树
- 1.2.1 构造最小生成树
- 1.2.2 Prim算法构造最小生成树
- 1.2.3 Kruskal算法构造最小生成树
- 1.2.4 两种算法的比较
- 1.3 最短路径
- 1.3.1 两点间最短路径
- 1.3.2 某源点到其他各点最短路径
- 1.3.3 Dijkstra
- 1.3.4 Floyd
- 1.4 拓扑排序
- 1.4.1 有向无环图DAG
- 1.4.2 AOV网
- 1.5 关键路径
- 1.5.1 求解关键路径
0 图的应用

1 生成树
生成树:所有顶点均由边连接在一起,但不存在回路的图。
也就是两个条件,顶点条件和边数条件,顶点都要保持连通,边数达到最少,没有回路。
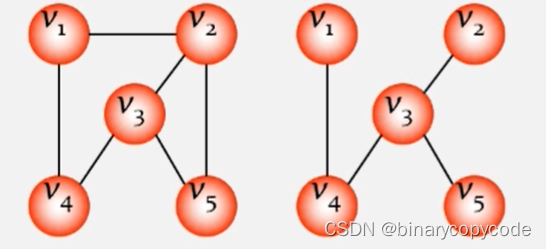
如右边的图,随便再加一条边就有回路了。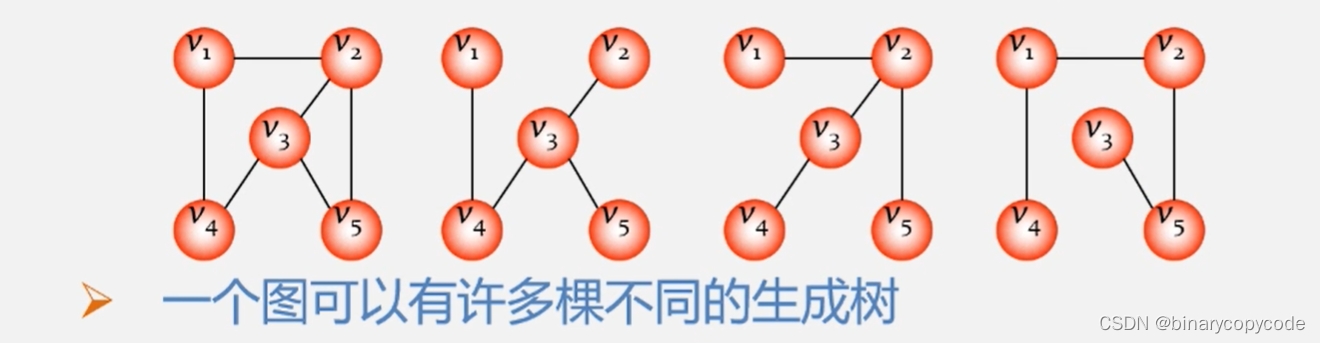
所有生成树都具有以下的共同特点:
- 生成树的顶点个数与图的顶点个数相同;
- 生成树是图的极小连通子图,去掉一条边则非连通;
- 一个有 n n n个顶点的连通图的生成树有 n − 1 n-1 n−1条边;
- 生成树中任意两个顶点间的路径是唯一的;
- 含有 n n n个顶点 n − 1 n-1 n−1条边的图不一定是生成树,如下图所示

因为生成树是连通的,每个顶点都要用边相连,上图是不连通的,有两个连通分量。
1.1 无向图的生成树
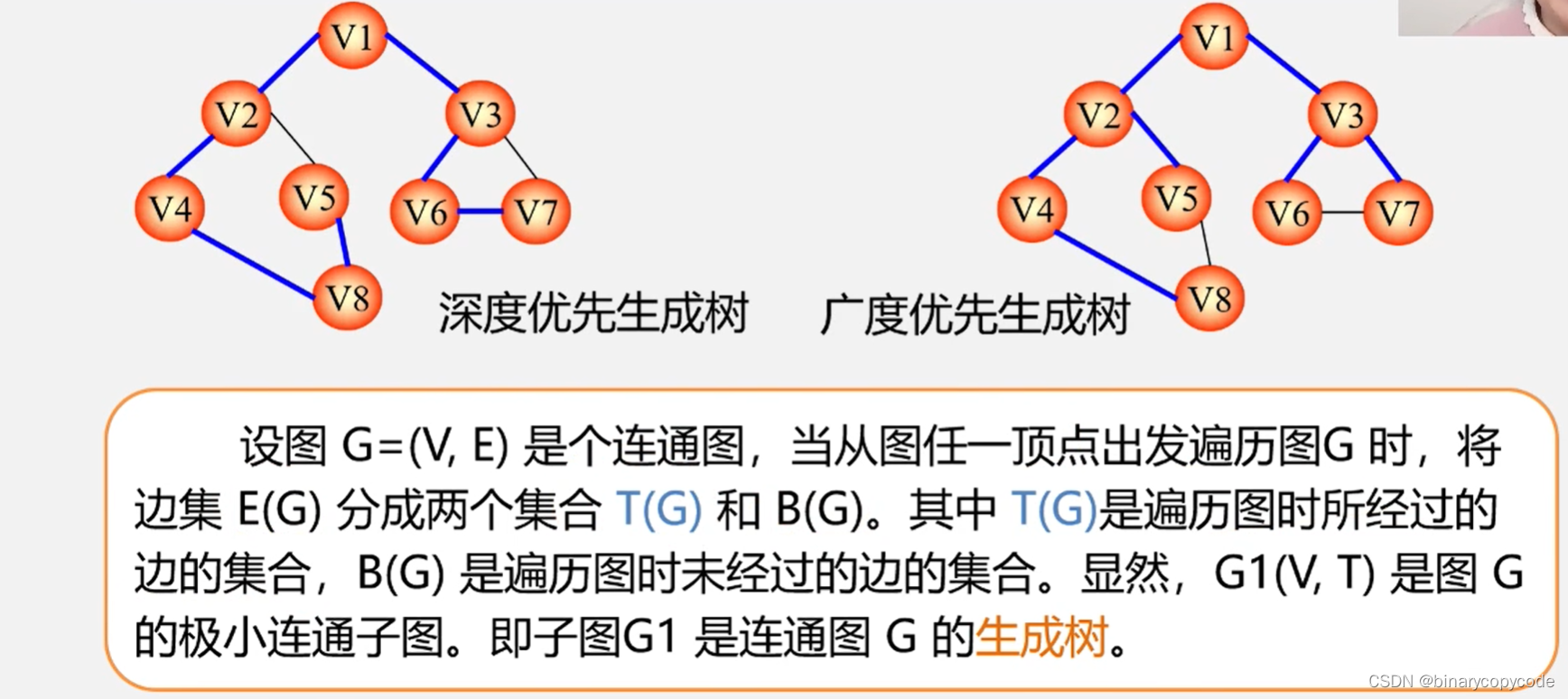
生成树要包含所有顶点,那么对图进行遍历,把走过的边全部加入到图当中。
遍历则采用DFS与BFS都可以。
用DFS生成的生成树就是DFS生成树。
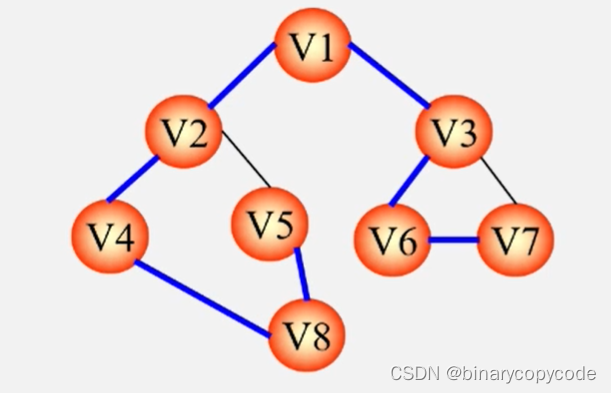
用BFS生成的生成树就是BFS生成树。
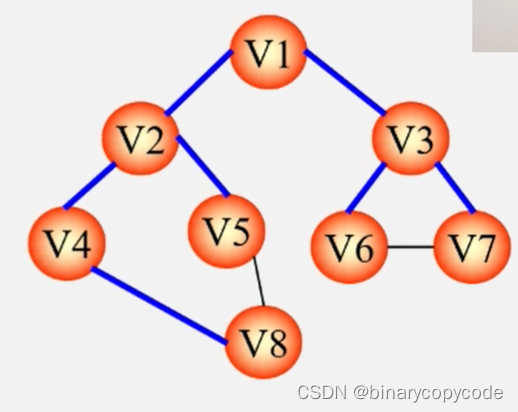
综上
1.2 最小生成树
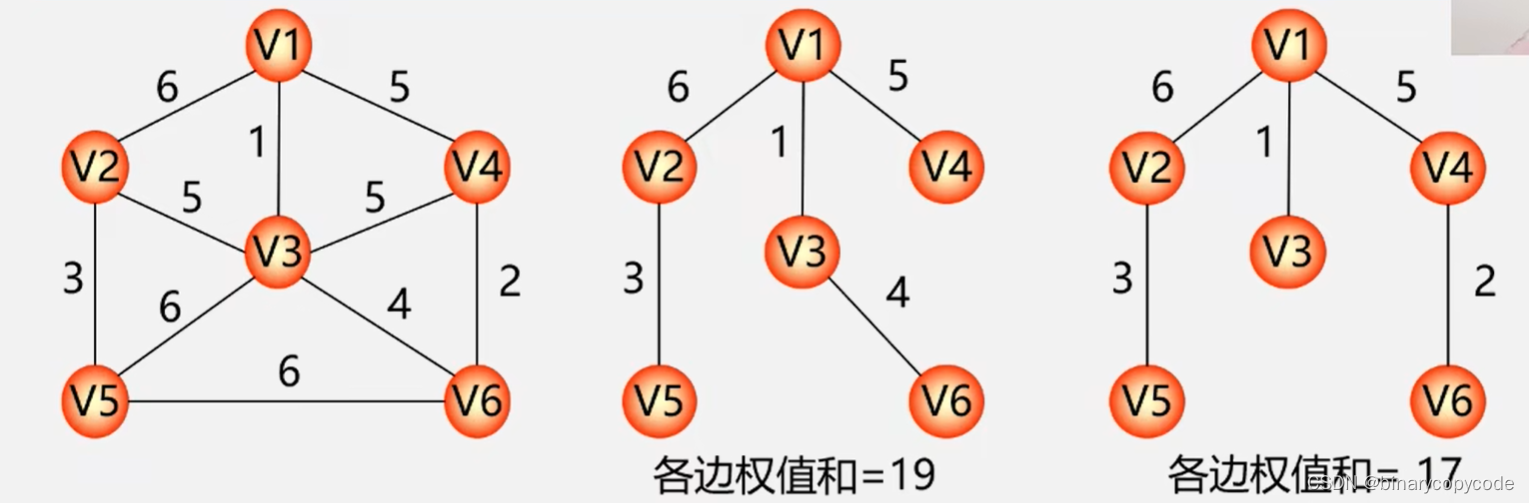
最小生成树:给定一无向网络在该网的所有生成树中,使得各边权值之和最小的那棵生成树称为该网的最小生成树,也叫最小代价生成树。
最小生成树可能是不唯一的。

1.2.1 构造最小生成树
构造最小生成树的算法很多,其中多数算法都利用了MST(Minimum Spanning Tree)的性质。
MST性质:
其实就是贪心算法,不断去找权值最小的边。
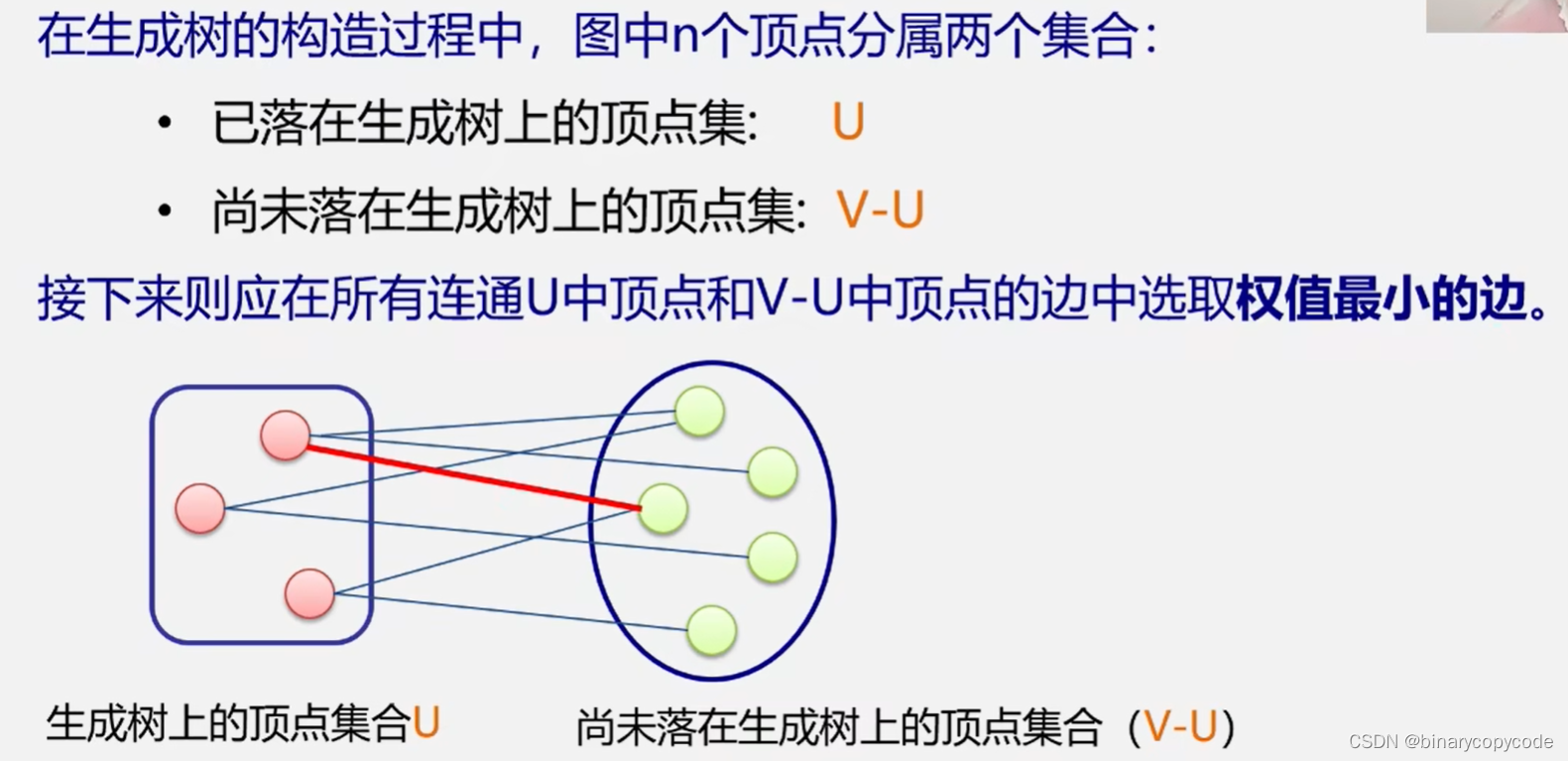
设 N = ( V , E ) N=(V, E) N=(V,E)以目是一个连通网, U U U是顶点集 V V V的一个非空子集。若边 ( u , v ) (u, v) (u,v)是一条具有最小权值的边,其中 u ∈ U , v ∈ V − U u∈U,v∈V-U u∈U,v∈V−U则必存在一棵包含边 ( u , v ) (u,v) (u,v)的最小生成树。
举例

现在 U = { v 1 } U=\{v_1\} U={v1},所以 V − U = { v 2 , v 3 , v 4 , v 5 , v 6 } V-U=\{v_2,v_3,v_4,v_5,v_6\} V−U={v2,v3,v4,v5,v6},所以 u ∈ U , v ∈ V − U u∈U,v∈V-U u∈U,v∈V−U当中,其中从 v 1 v_1 v1到 v 3 v_3 v3是最小的,权值为1,存在这个权值最小的边,这条边一定会包含在某个最下生成树当中。
1.2.2 Prim算法构造最小生成树
算法思想:

1.2.3 Kruskal算法构造最小生成树
相比Prim算法更加贪心,直截了当贪心,前提不成环。这次开始就把所有顶点都加入到最小生成树上面去。不过并不包括边,这时边的集合都是空集,没包含边,彼此之间不连通。

然后直接在边集合当中选权值最小的边,直接加入。
以此类推,选到所有顶点都连通为止(前提不能形成回路)(n个点,n-1条边)。
1.2.4 两种算法的比较

Prim是选择点加入的,而Kruskal是选择边的。选择边的时候和顶点数是没关系的。
1.3 最短路径
1.3.1 两点间最短路径
从起点走向终点,并非要n个节点都包括,也并非要n-1条边。
直到找到路径长度最短的一条路径。
这种最短路径也称为单源的最短路径,采用Dijkstra算法。
1.3.2 某源点到其他各点最短路径
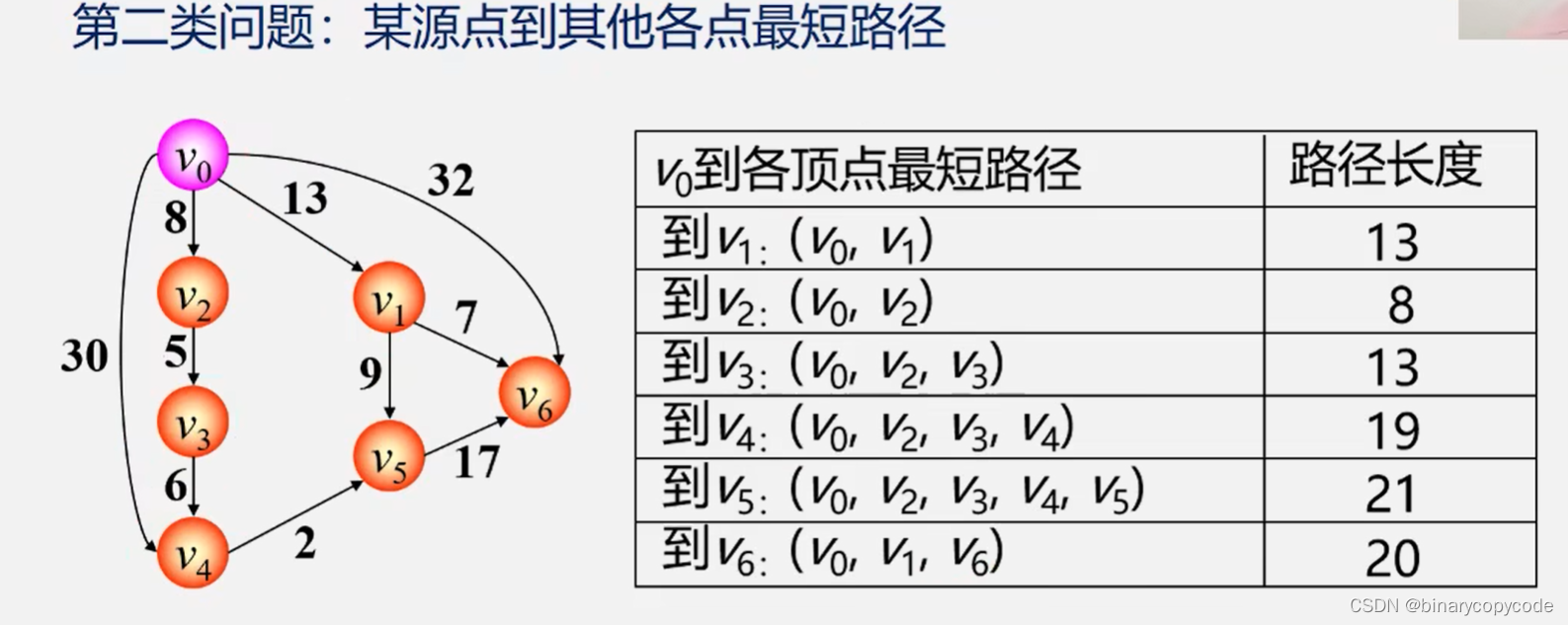
所有顶点的最短路径,统一使用Floyd弗洛伊德算法。
1.3.3 Dijkstra
其时间复杂度为 O ( n 3 ) O(n^3) O(n3)

按照路径长度递增次序产生最短路径,启发式贪心算法。

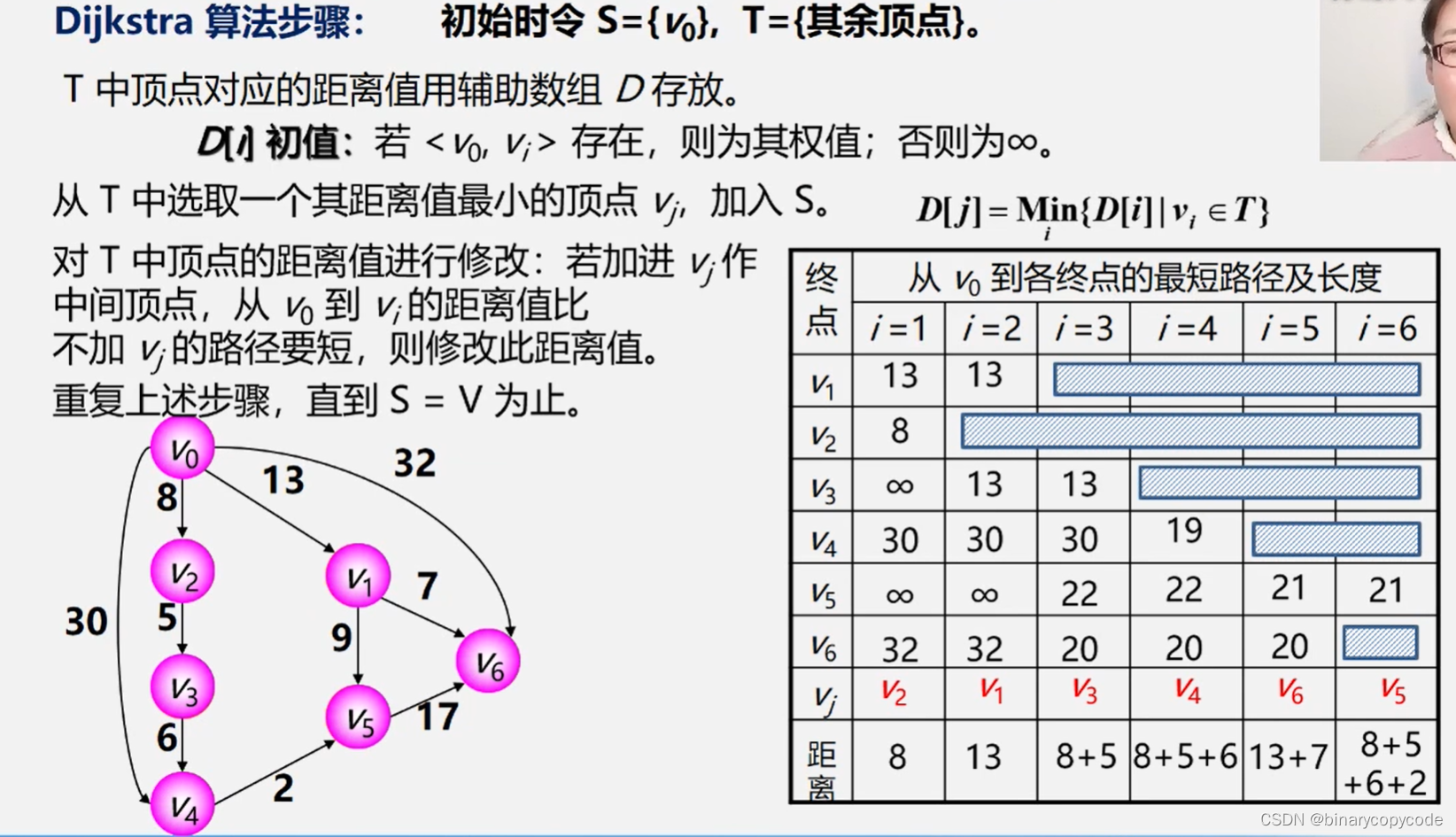
启发式算法,先找最短的,后面再及时更新,具体过程可以看王老师的视频。
1.3.4 Floyd
其时间复杂度为 O ( n 3 ) O(n^3) O(n3)
算法思想:
- 逐个顶点试探
- 从少,到的所有可能存在的路径中
- 选出一条长度最短的路径

求最短路径的步骤:
初始时设置一个 n n n阶方阵,令其对角线元素(到自身的路径)为0,若存在弧 < v i , v j > <v_i, v_j> <vi,vj>,则对应元素为权值;否则为 ∞ ∞ ∞。
逐步试着在原直接路径中增加中间顶点,若加入中间顶点后路径变短,则修改之;否则,维持原值。所有顶点试探完毕,算法结束。

1.4 拓扑排序
1.4.1 有向无环图DAG


AOV网以顶点表示活动;AOE网用弧表示活动(子工程)。
AOV网用来解决拓扑排序,AOE网用来解决关键路径问题。
拓扑排序的一个小例子:
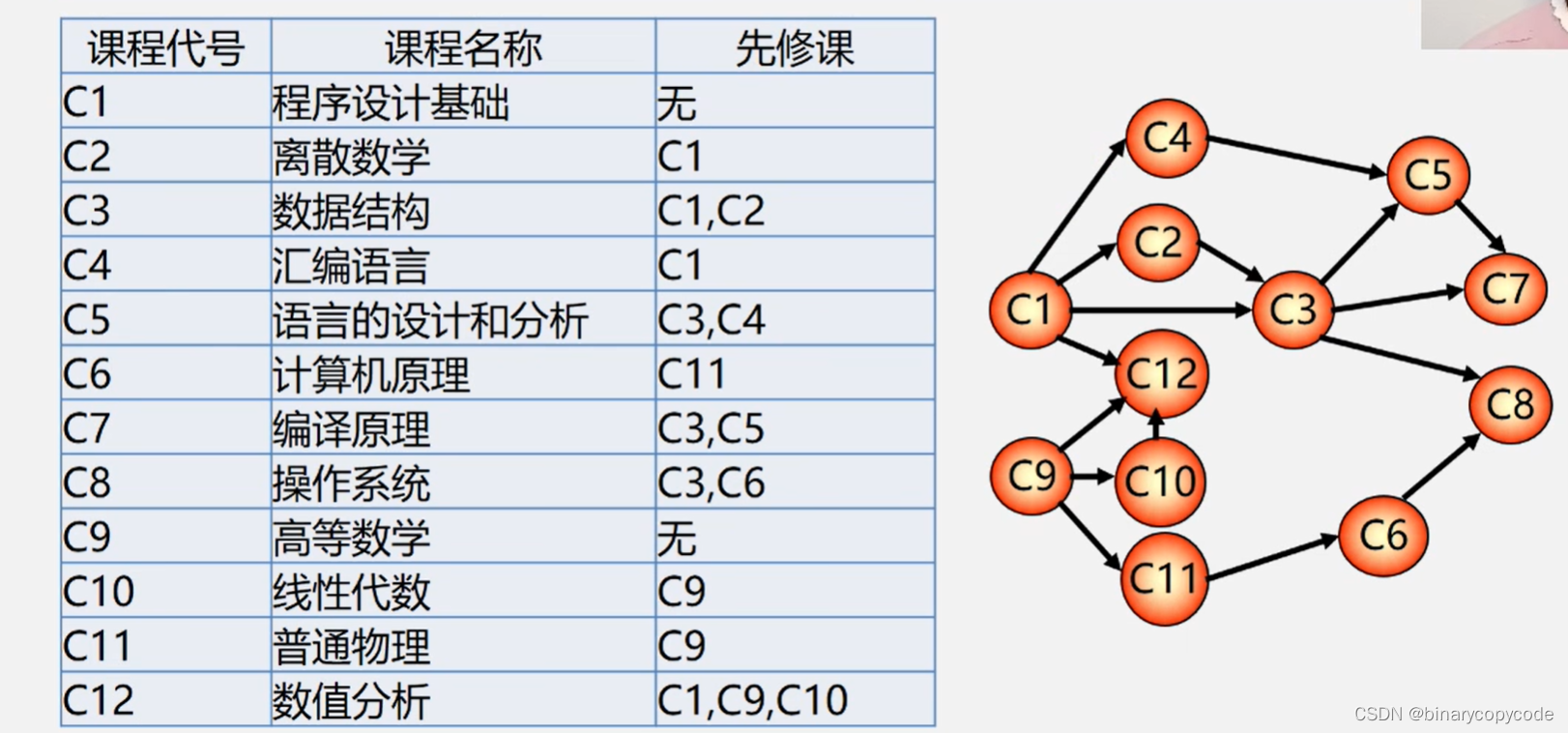
1.4.2 AOV网

问题:如何判断AOV网中是否存在回路?
答:

所有顶点都能加入拓扑排序的话,就一定没有网。
拓扑排序。
将网变成一个线性序列的过程就是拓扑排序。

拓扑排序的步骤:
- 首先构建好AOV网
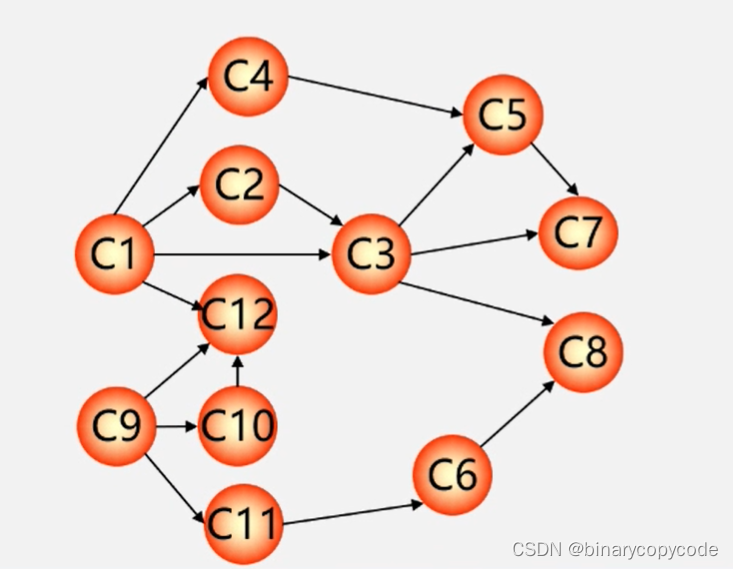
- 在有向图中选一个没有前驱的顶点且输出(例如C1和C9)
- 假设选了C1,在有向图当中删除该顶点和所有以它为尾的弧(C1发出的弧)(即C1与C2,C4,C12的弧)
- 重复上述两步,直至全部顶点均已输出;或者当图中不存在无前驱的顶点为止

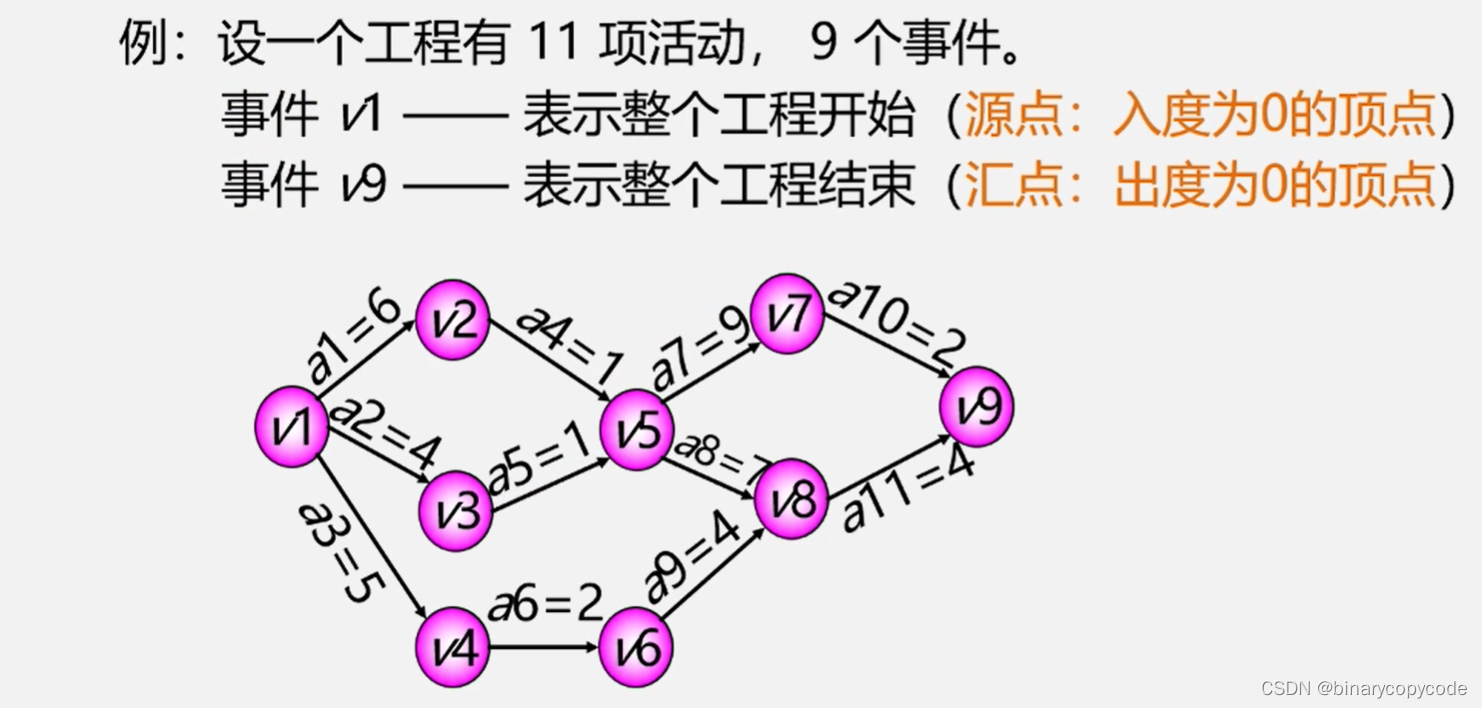
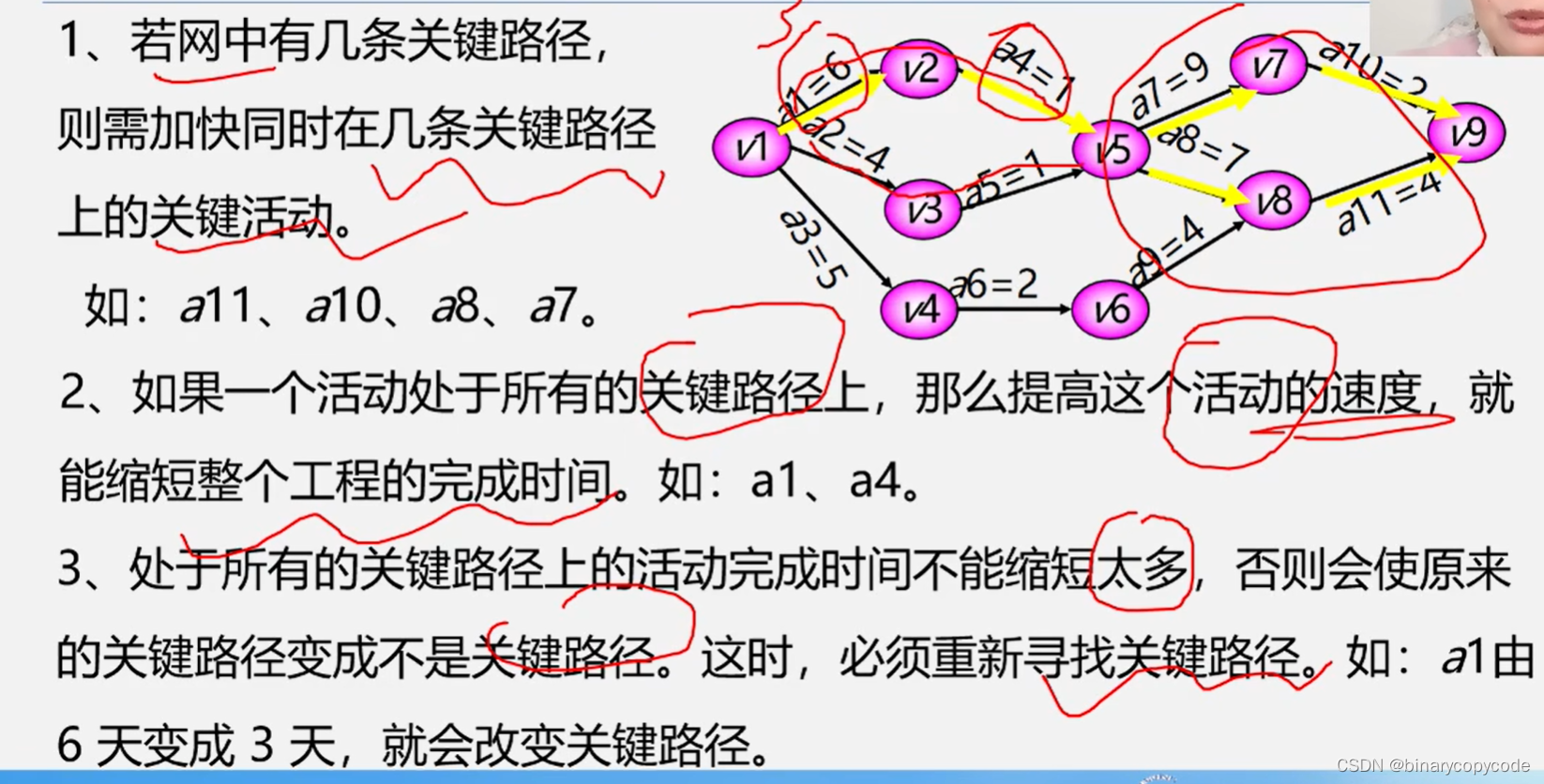
1.5 关键路径
制定计划,查找关键路径。
关键路径就是从源点到汇点路径长度(权值之和)最长(大)的路径。
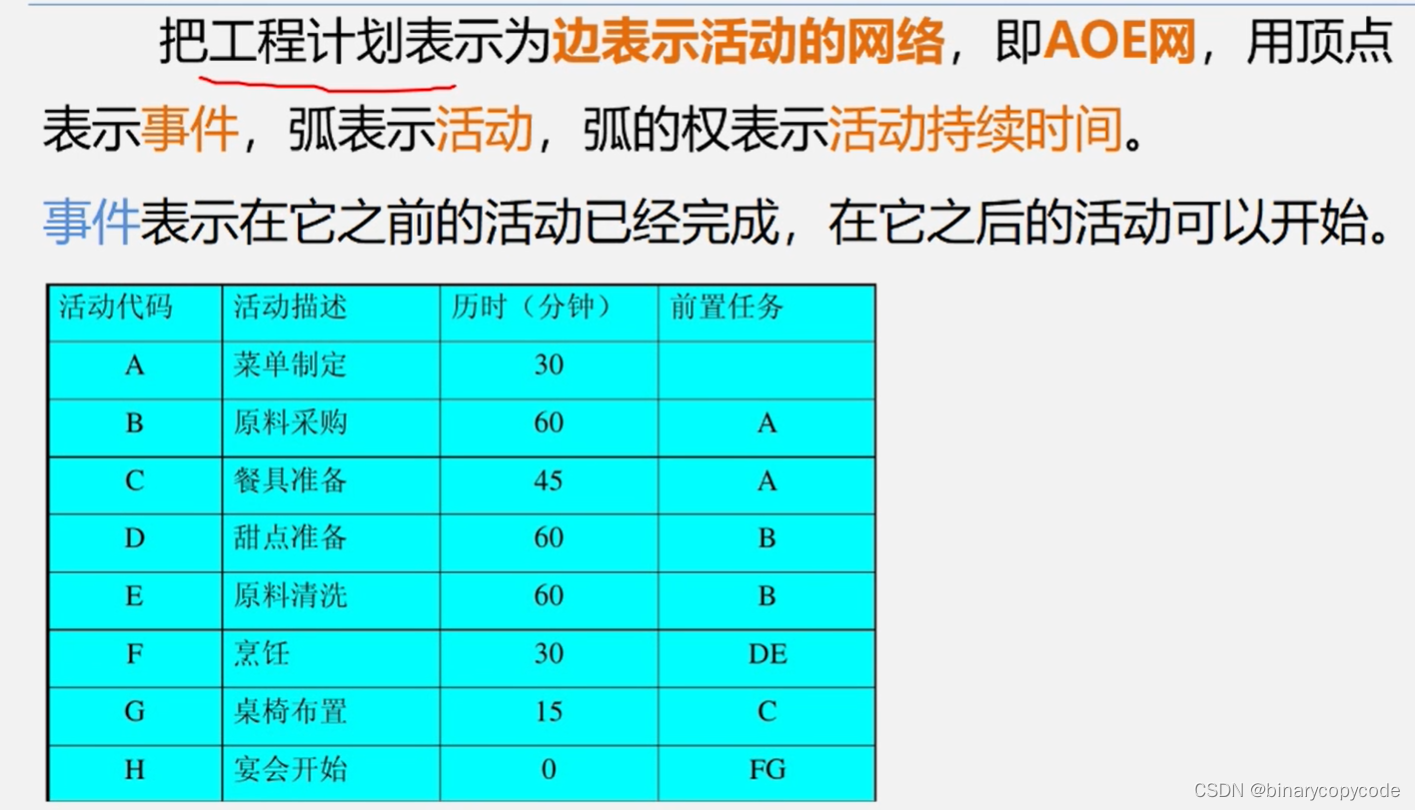
按照任务需求,构建有权图。
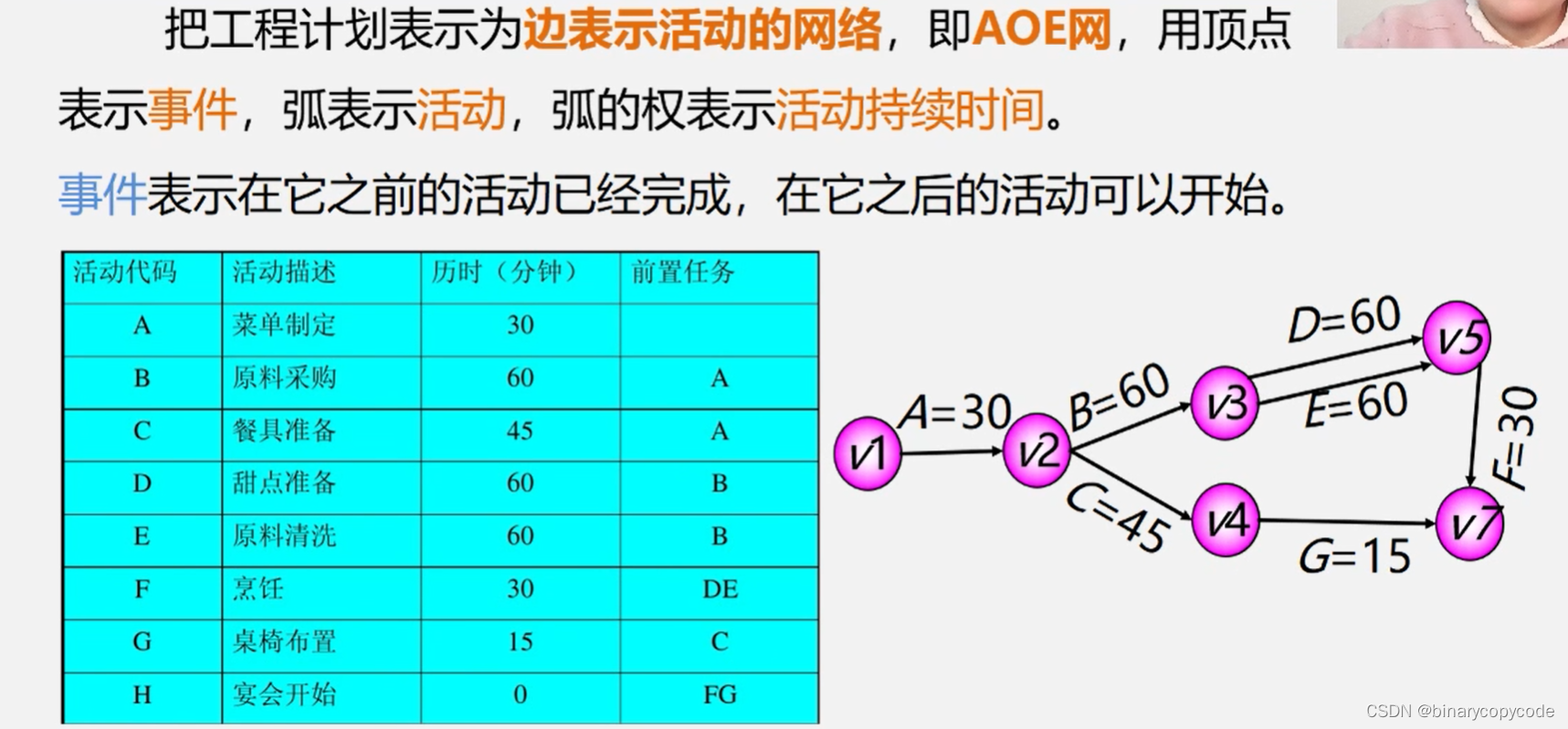
举例:
对于上方AOE网,我们关心两个问题:
- 完成整项女程至少需要多少时间?
- 哪些活动是影响工程进度的关键?
以上答为关键路径与路径长度。
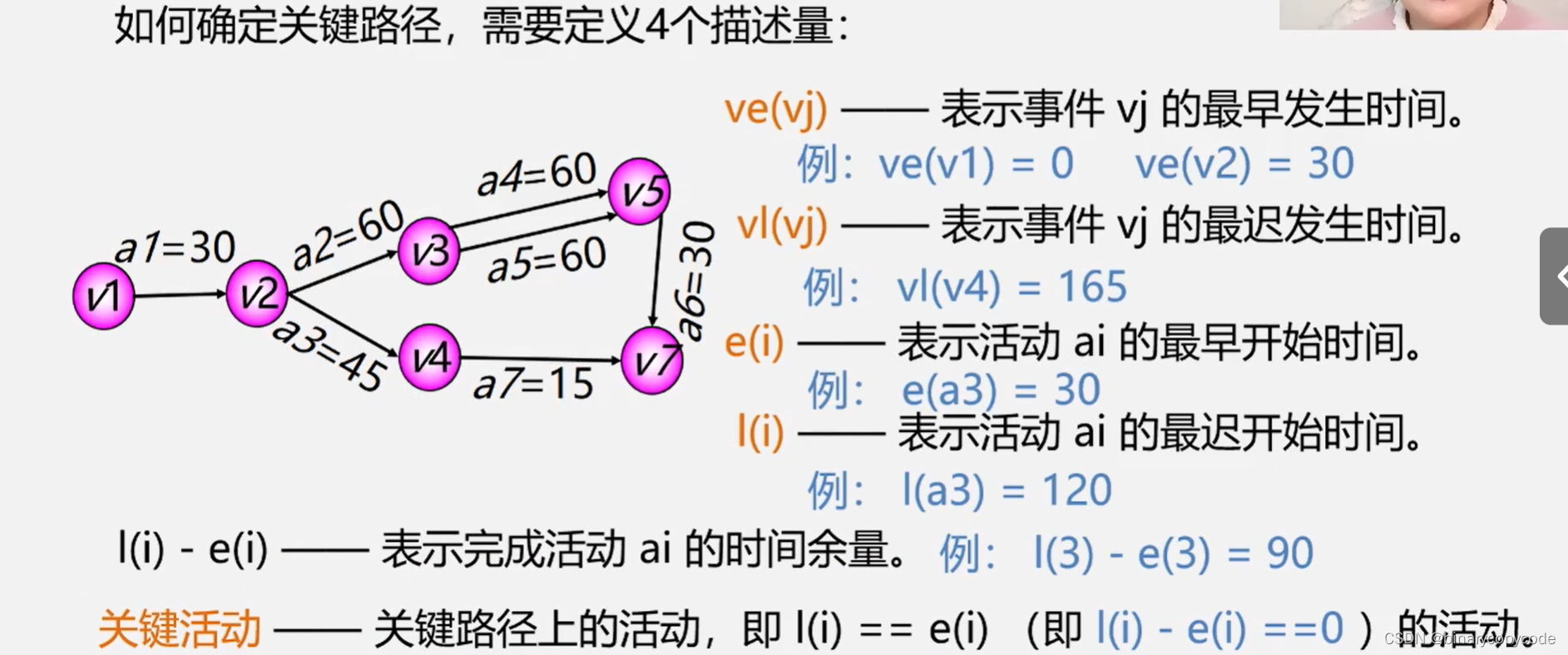
1.5.1 求解关键路径
四个有用的量:


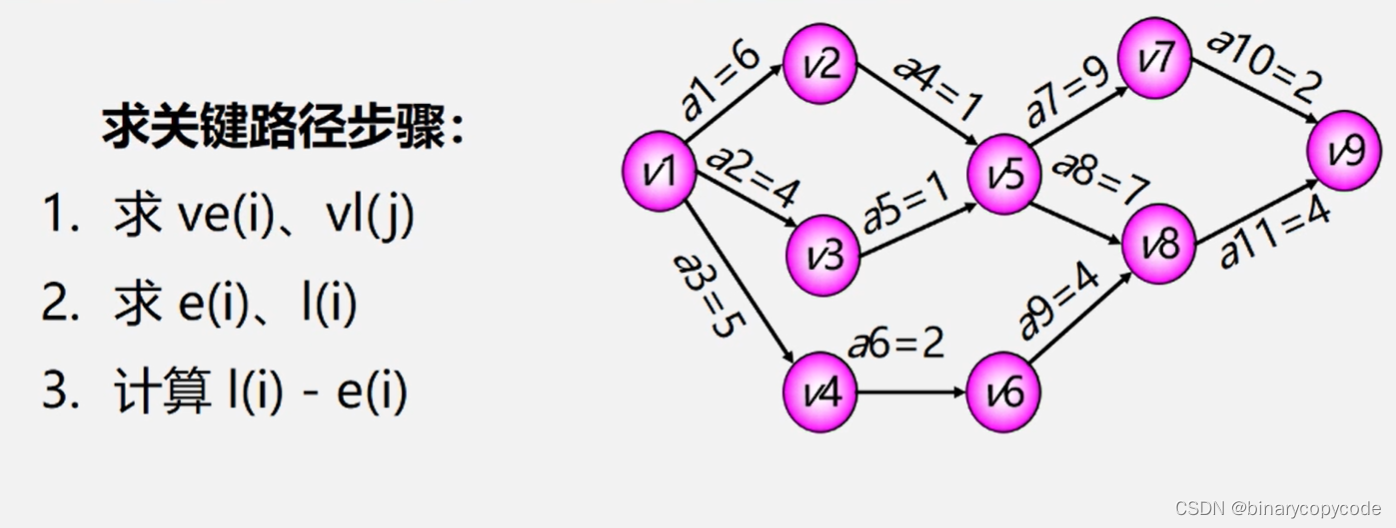
求关键路径的步骤:

相关文章:

DSA之图(4):图的应用
文章目录 0 图的应用1 生成树1.1 无向图的生成树1.2 最小生成树1.2.1 构造最小生成树1.2.2 Prim算法构造最小生成树1.2.3 Kruskal算法构造最小生成树1.2.4 两种算法的比较 1.3 最短路径1.3.1 两点间最短路径1.3.2 某源点到其他各点最短路径1.3.3 Dijkstra1.3.4 Floyd 1.4 拓扑排…...

[SQL挖掘机] - 窗口函数 - row_number
介绍: row_number() 是一种常用的窗口函数,它为结果集中的每一行分配一个唯一的数字。这个数字的分配基于指定的排序顺序,并且不会跳过相同的排名。 用法: row_number() 函数的语法如下: row_number() over ([partition by 列名1, 列名2,…...
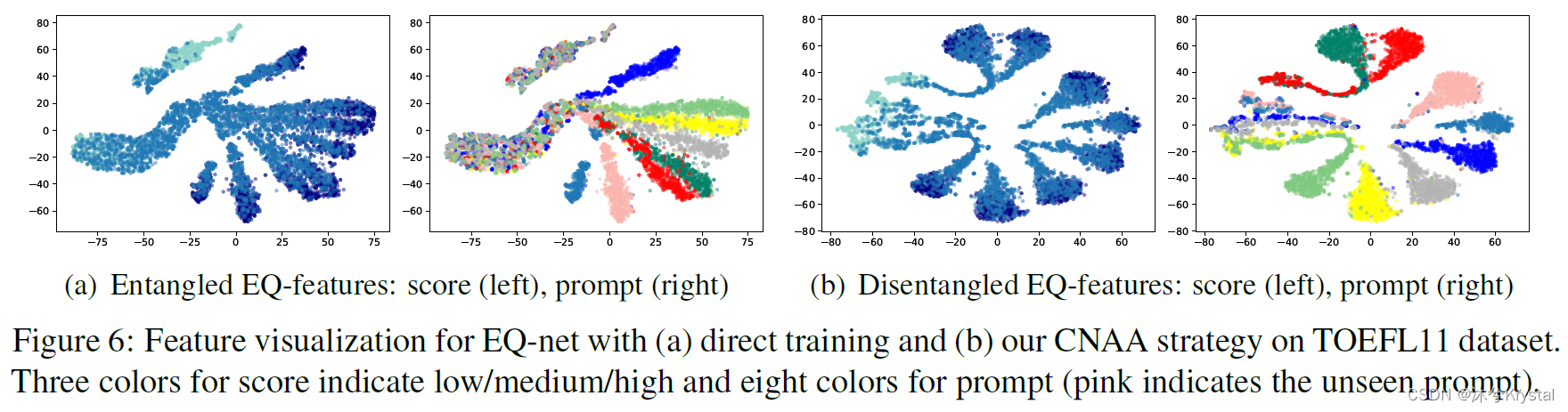
【论文阅读】通过解缠绕表示学习提升领域泛化能力用于主题感知的作文评分
摘要 本文工作聚焦于从领域泛化的视角提升AES模型的泛化能力,在该情况下,目标主题的数据在训练时不能被获得。本文提出了一个主题感知的神经AES模型(PANN)来抽取用于作文评分的综合的表示,包括主题无关(pr…...

二分查找P1873 [COCI2011-2012#5] EKO / 砍树
P1873 [COCI2011-2012#5] EKO / 砍树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 这个题就是给新手练手的,在那个位置上在进行,寻找合适的砍树高度,下面在介绍一个二分查找的模板 int binarySearch(vector<int>& nums, int t…...

【BOOST程序库】正则表达式相关操作
基本概念这里不解释了,代码中详细解释了BOOST程序库中对于正则表达式常用方法的详细用法。 #include <iostream> #include <string>//正则表达式头文件 #include <boost/xpressive/xpressive.hpp>int main() {//声明正则:boost::pres…...

阿里云国际版在使用过程中应该注意什么呢?
为确保系统稳定性,用户不得进行以下操作。否则,阿里云可能无法解决由以下违规操作引起的问题: 1) Windows系统中的PV Drivers 程序不可删除 PV Drivers程序为服务器虚拟化驱动程序,请不要针对该程序进行任何操作,如果删…...

Flutter Provider 共享状态管理
在使用Provider的时候,我们主要关心三个概念: ChangeNotifier:真正数据(状态)存放的地方ChangeNotifierProvider:Widget树中提供数据(状态)的地方,会在其中创建对应的Ch…...

std vector 用法
使用vector,需添加头文件#include,要使用sort或find,则需要添加头文件#include。函数封装在命名空间std中,使用:using namespace std; 1、vector的初始化 std::vector<int> nVec; // 空对象 std::vecto…...

vue vite ts electron ipc addon-napi c arm64
初始化 因网络问题建议使用 cnpm 代替 npm npm init vue # 全选 yes npm i # 进入项目目录后使用 npm i electron electron-builder -D npm i commander -D # 额外组件electron 新建 plugins、src/electron 文件夹 添加 src/electron/background.ts 属于主进程 ipcMain.o…...

机器人科普--AGILOX 叉车
机器人科普--AGILOX 叉车 1 概述2 导航3 驱动轮组4 叉举参考 1 概述 AGILOX 叉车,不需要画地图路径,很厉害。 2 导航 中间路径自由导航,末端规划出轨迹路线,并使用优良的控制器做轨迹追踪。 AGILOX | 10 Min setu…...
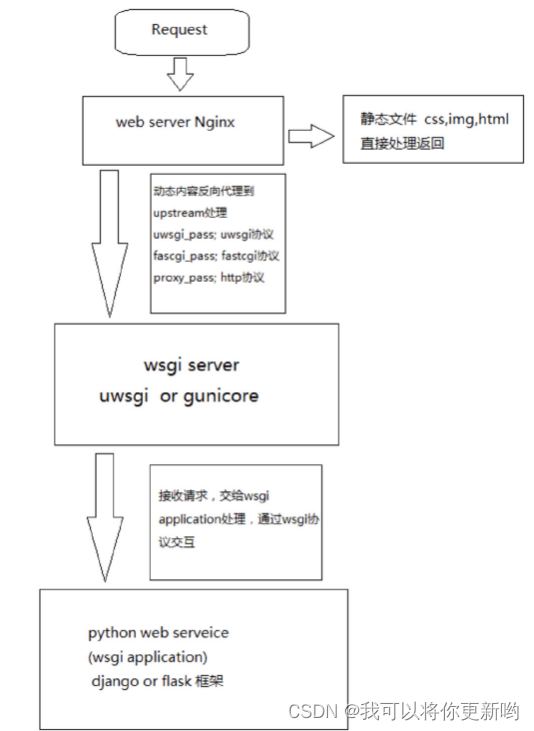
Django的生命周期流程图(补充)、路由层urls.py文件、无名分组和有名分组、反向解析(无名反向解析、有名反向解析)、路由分发、伪静态
一、orm的增删改查方法(补充) 1. 查询resmodels.表名(类名).objects.all()[0]resmodels.表名(类名).objects.filter(usernameusername, passwordpassword).all()res models.表名(类名).objects.first() # 判断,判断数据是否有# res如果查询…...

selenium交互代码
一:selenium交互 用selenium打开网页后,也可以做一系列真人的操作,也就是利用selenium和浏览器进行交互,可利用以下几个函数进行操作: input.send_keys() 传递输入内容给某输入框button.click() 点击某按钮browser.e…...

下载远程服务器文件
业务需求:下载某云盘的视频文件存储到本地 测试代码 RequestMapping("testVideo")public String test() {try {SimpleDateFormat DATE_FORMAT new SimpleDateFormat("yyyy/MM/dd/");//组装本地保存地址StringBuilder filePath new StringBuilder(StoreP…...

[SQL挖掘机] - 索引
介绍: 当你在数据库中进行查询时,索引是一种用于提高查询性能的重要工具。索引是对表中的一列或多列进行排序的数据结构,它可以快速定位到满足特定条件的记录,从而减少了查询所需的时间和资源。 在数据库中使用索引的主要好处包括ÿ…...
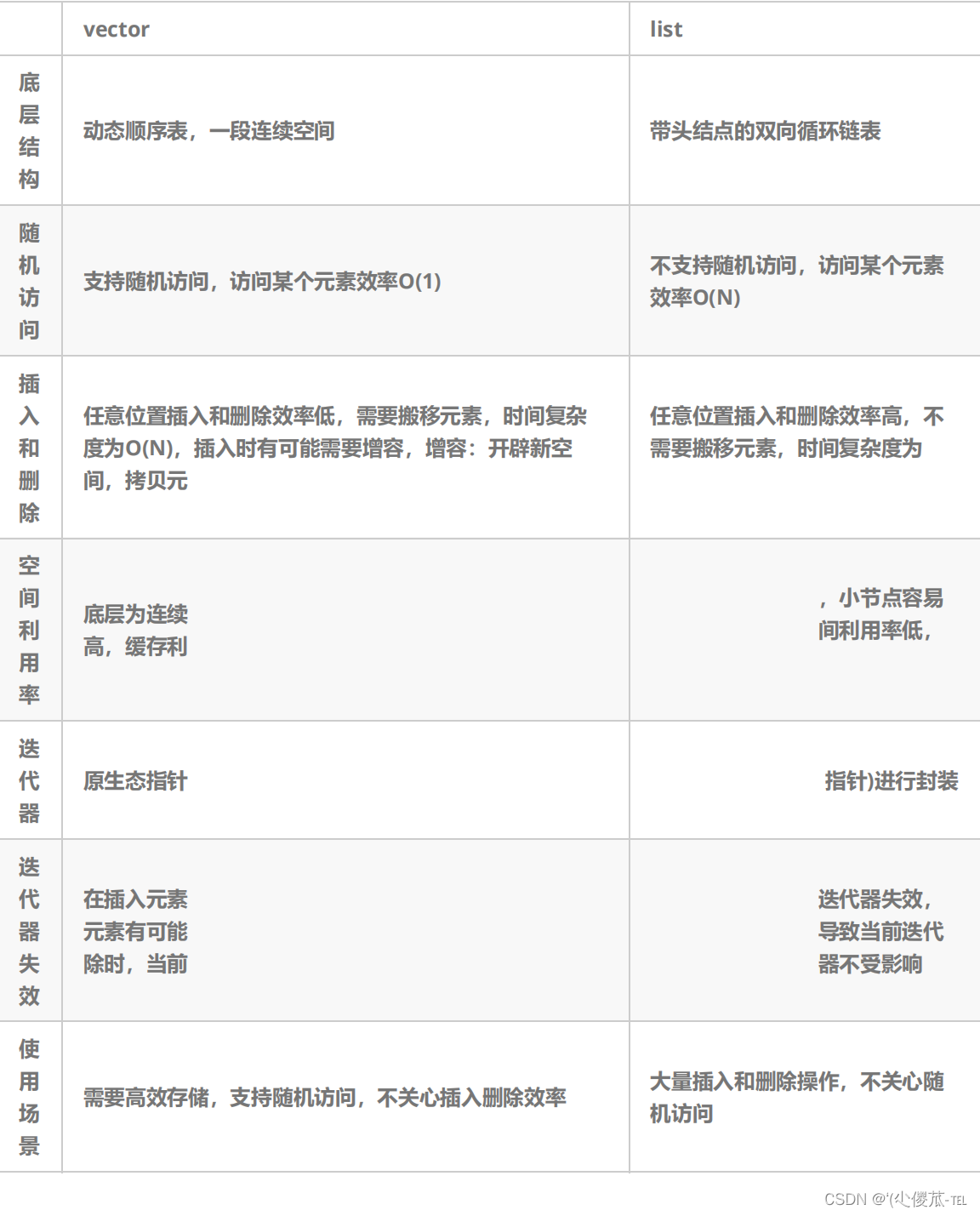
C++STL库中的list
文章目录 list的介绍及使用 list的常用接口 list的模拟实现 list与vector的对比 一、list的介绍及使用 1. list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。 2. list的底层是双向带头循环链表结构,双向带头循…...
【LeetCode 75】第十七题(1493)删掉一个元素以后全为1的最长子数组
目录 题目: 示例: 分析: 代码运行结果: 题目: 示例: 分析: 给一个数组,求删除一个元素以后能得到的连续的最长的全是1的子数组。 我们可以先单独统计出连续为1的子数组分别长度…...
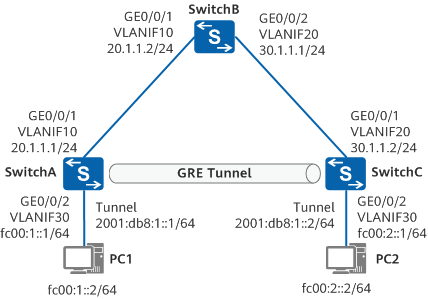
配置IPv6 over IPv4 GRE隧道示例
组网需求 如图1,两个IPv6网络分别通过SwitchA和SwitchC与IPv4公网中的SwitchB连接,客户希望两个IPv6网络中的PC1和PC2实现互通。 其中PC1和PC2上分别指定SwitchA和SwitchC为自己的缺省网关。 图1 配置IPv6 over IPv4 GRE隧道组网图 配置思路 要实现I…...
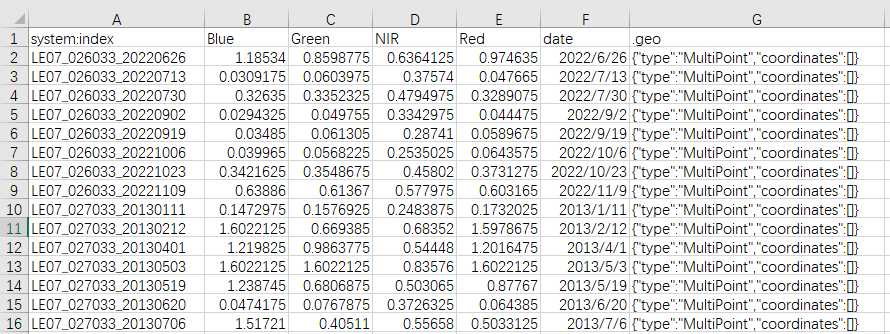
Google Earth Engine谷歌地球引擎提取多波段长期反射率数据后绘制折线图并导出为Excel
本文介绍在谷歌地球引擎GEE中,提取多年遥感影像多个不同波段的反射率数据,在GEE内绘制各波段的长时间序列走势曲线图,并将各波段的反射率数据与其对应的成像日期一起导出为.csv文件的方法。 本文是谷歌地球引擎(Google Earth Engi…...
第三大的数
414、第三大的数 class Solution {public int thirdMax(int[] nums) {Arrays.sort(nums);int tempnums[0];int ansnums[0];int count 0;// if(nums.length<3){// return nums[nums.length-1];// }// else {for(int inums.length-1;i>0;i--){if (nums[i]>nums[i…...

正则表达式中的方括号[]有什么用?
在正则表达式中,方括号 [] 是用于定义字符集合的元字符。它在正则表达式中有以下作用: 匹配字符集合中的任意一个字符:方括号中列出的字符,表示在这个位置可以匹配这些字符中的任意一个。例如,[abc] 将匹配任意一个字符…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
