重新审视MHA与Transformer
本文将基于PyTorch源码重新审视MultiheadAttention与Transformer。事实上,早在一年前博主就已经分别介绍了两者:各种注意力机制的PyTorch实现、从零开始手写一个Transformer,但当时的实现大部分是基于d2l教程的,这次将基于PyTorch源码重新实现一遍。
目录
- 1. MultiheadAttention
- 1.1 思路
- 1.2 源码
- 1.3 极简版MHA(面试用)
- 2. Transformer
- 3. Q&A
- 1. MHA的参数量?FLOPs?时间复杂度?
- 2. Transformer的总参数量?模型占用显存?
- 3. Transformer的FLOPs?
- 4. 参数量、FLOPs、时间复杂度汇总
- Ref
1. MultiheadAttention
1.1 思路
回顾多头注意力,其公式如下:
MHA ( Q , K , V ) = Concat ( head 1 , ⋯ , head h ) W O head i = Attn ( Q W i Q , K W i K , V W i V ) \text{MHA}(Q,K,V)=\text{Concat}(\text{head}_1,\cdots,\text{head}_h)W^O \\ \text{head}_i=\text{Attn}(QW_i^Q,KW_i^K,VW_i^V) MHA(Q,K,V)=Concat(head1,⋯,headh)WOheadi=Attn(QWiQ,KWiK,VWiV)
其中 W i Q ∈ R d m o d e l × d k W_i^Q\in \mathbb{R}^{d_{model}\times d_k} WiQ∈Rdmodel×dk, W i K ∈ R d m o d e l × d k W_i^K\in \mathbb{R}^{d_{model}\times d_k} WiK∈Rdmodel×dk, W i V ∈ R d m o d e l × d v W_i^V\in \mathbb{R}^{d_{model}\times d_v} WiV∈Rdmodel×dv, W O ∈ R h d v × d m o d e l W^O\in \mathbb{R}^{hd_v\times d_{model}} WO∈Rhdv×dmodel,且 d k = d v = d m o d e l / h d_k=d_v=d_{model}/h dk=dv=dmodel/h。
如果记 d h e a d = d m o d e l / h d_{head}=d_{model}/h dhead=dmodel/h,则 W i Q , W i K , W i V W_i^Q,W_i^K,W_i^V WiQ,WiK,WiV 的形状均为 ( d m o d e l , d h e a d ) (d_{model},d_{head}) (dmodel,dhead), W O W^O WO 的形状为 ( d m o d e l , d m o d e l ) (d_{model},d_{model}) (dmodel,dmodel)。
先不考虑batch和mask的情形,在只有一个头的情况下( h = 1 h=1 h=1),MHA的计算方式为
class MHA(nn.Module):def __init__(self, d_model):super().__init__()self.w_q = nn.Parameter(torch.empty(d_model, d_model))self.w_k = nn.Parameter(torch.empty(d_model, d_model))self.w_v = nn.Parameter(torch.empty(d_model, d_model))self.w_o = nn.Parameter(torch.empty(d_model, d_model))self._reset_parameters()def _reset_parameters(self):for p in self.parameters():if p.dim() > 1:nn.init.xavier_uniform_(p)def forward(self, query, key, value):"""Args:query: (n, d_model),n是query的个数,m是key-value的个数key: (m, d_model)value: (m, d_model)"""q = query @ self.w_qk = key @ self.w_kv = value @ self.w_vattn_logits = q @ k.transpose(0, 1) / math.sqrt(q.size(1)) # attn_logits: (n, m)attn_probs = F.softmax(attn_logits, dim=-1)attn_output = attn_probs @ v # attn_output: (n, d_model)return attn_output, attn_probs
现在考虑 h = 2 h=2 h=2 的情形,此时一共需要 3 ⋅ 2 + 1 = 7 3\cdot2+1=7 3⋅2+1=7 个参数矩阵
class MHA(nn.Module):def __init__(self, d_model):super().__init__()self.w_q_1 = nn.Parameter(torch.empty(d_model, d_model // 2))self.w_k_1 = nn.Parameter(torch.empty(d_model, d_model // 2))self.w_v_1 = nn.Parameter(torch.empty(d_model, d_model // 2))self.w_q_2 = nn.Parameter(torch.empty(d_model, d_model // 2))self.w_k_2 = nn.Parameter(torch.empty(d_model, d_model // 2))self.w_v_2 = nn.Parameter(torch.empty(d_model, d_model // 2))self.w_o = nn.Parameter(torch.empty(d_model, d_model))self._reset_parameters()def _reset_parameters(self):for p in self.parameters():if p.dim() > 1:nn.init.xavier_uniform_(p)def forward(self, query, key, value):"""Args:query: (n, d_model),n是query的个数,m是key-value的个数key: (m, d_model)value: (m, d_model)"""q_1 = query @ self.w_q_1k_1 = key @ self.w_k_1v_1 = value @ self.w_v_1q_2 = query @ self.w_q_2k_2 = key @ self.w_k_2v_2 = value @ self.w_v_2attn_logits_1 = q_1 @ k_1.transpose(0, 1) / math.sqrt(q_1.size(1))attn_probs_1 = F.softmax(attn_logits_1, dim=-1)attn_output_1 = attn_probs_1 @ v_1attn_logits_2 = q_2 @ k_2.transpose(0, 1) / math.sqrt(q_2.size(1))attn_probs_2 = F.softmax(attn_logits_2, dim=-1)attn_output_2 = attn_probs_2 @ v_2attn_output = torch.cat([attn_output_1, attn_output_2], dim=-1) @ self.w_o # attn_output: (n, d_model)attn_probs = torch.stack([attn_probs_1, attn_probs_2], dim=0) # attn_probs: (2, n, m),其中2是头数return attn_output, attn_probs
可以看到代码量已经增加了不少,如果扩展到 h h h 个头的情形,则需要 3 h + 1 3h+1 3h+1 个参数矩阵。手动去一个个声明显然不现实,因为 h h h 是动态变化的,而用for循环创建又略显笨拙,有没有更简便的方法呢?
在上面的代码中,我们用小写 q q q 来代表查询 Q Q Q 经过投影后的结果( k , v k,v k,v 同理),即
q i = Q W i Q , i = 1 , 2 , ⋯ , h q_i=QW_i^Q,\quad i =1,2,\cdots,h qi=QWiQ,i=1,2,⋯,h
其中 Q Q Q 的形状为 ( n , d m o d e l ) (n,d_{model}) (n,dmodel), q i q_i qi 的形状为 ( n , d h e a d ) (n,d_{head}) (n,dhead),且有
h e a d i = softmax ( q i k i T d h e a d ) v i head_i=\text{softmax}\left(\frac{q_ik_i^{T}}{\sqrt{d_{head}}}\right)v_i headi=softmax(dheadqikiT)vi
注意到
[ q 1 , q 2 , ⋯ , q h ] = Q [ W 1 Q , W 2 Q , ⋯ , W h Q ] (1) [q_1,q_2,\cdots,q_h]=Q[W_1^Q,W_2^Q,\cdots,W_h^Q]\tag{1} [q1,q2,⋯,qh]=Q[W1Q,W2Q,⋯,WhQ](1)
如果记 q ≜ [ q 1 , q 2 , ⋯ , q h ] q\triangleq [q_1,q_2,\cdots,q_h] q≜[q1,q2,⋯,qh], W Q ≜ [ W 1 Q , W 2 Q , ⋯ , W h Q ] W^Q\triangleq [W_1^Q,W_2^Q,\cdots,W_h^Q] WQ≜[W1Q,W2Q,⋯,WhQ],则 W Q W^Q WQ 的形状为 ( d m o d e l , d m o d e l ) (d_{model},d_{model}) (dmodel,dmodel),与 h h h 无关, q q q 的形状为 ( n , d m o d e l ) (n,d_{model}) (n,dmodel)。这样一来,我们就不需要一个个声明 W i Q W_i^Q WiQ 了,并且可以一次性存储所有的 q i q_i qi。
要计算 h e a d 1 head_1 head1,我们需要能够从 q q q 中取出 q 1 q_1 q1( k , v k,v k,v 同理),所以我们期望 q q q 的形状是 ( h , n , d h e a d ) (h,n,d_{head}) (h,n,dhead),从而 q [ 1 ] q[1] q[1] 就是 q 1 q_1 q1(这里下标从 1 1 1 开始)。
📝 当然也可以是 ( n , h , d h e a d ) (n,h,d_{head}) (n,h,dhead) 等形状,但必须要确保形状里含且只含这三个数字。之所以把 h h h 放在第一个维度是为了方便索引和后续计算。
同理可知 k , v k,v k,v 的形状均为 ( h , m , d h e a d ) (h,m,d_{head}) (h,m,dhead)。我们可以视 h h h 所在的维度为批量维,从而可以执行批量乘法 torch.bmm 来一次性算出 h h h 个头的结果。
q = torch.randn(h, n, d_head)
k = torch.randn(h, m, d_head)
v = torch.randn(h, m, d_head)# @和torch.bmm的效果相同,但写法更简洁
attn_logits = q @ k.transpose(1, 2) / math.sqrt(q.size(2))
attn_probs = F.softmax(attn_logits, dim=-1)
attn_output = attn_probs @ v # attn_output: (h, n, d_head)
h h h 个头的结果存储在形状为 ( h , n , d h e a d ) (h,n,d_{head}) (h,n,dhead) 的张量中,那我们如何把这 h h h 个结果concat在一起呢?注意到我们实际上是将 h h h 个形状为 ( n , d h e a d ) (n,d_{head}) (n,dhead) 的张量横向concat为一个形状为 ( n , d m o d e l ) (n,d_{model}) (n,dmodel) 的张量,因此只需执行如下的形状变换:
( h , n , d h e a d ) → ( n , h , d h e a d ) → ( n , h ⋅ d h e a d ) = ( n , d m o d e l ) (2) (h,n,d_{head})\to(n,h,d_{head})\to(n,h\cdot d_{head})=(n,d_{model}) \tag{2} (h,n,dhead)→(n,h,dhead)→(n,h⋅dhead)=(n,dmodel)(2)
n = attn_output.size(1)
attn_output = attn_output.transpose(0, 1).reshape(n, -1)
⚠️ 注意,切勿直接将 ( h , n , d h e a d ) (h,n,d_{head}) (h,n,dhead) reshape成 ( n , d m o d e l ) (n,d_{model}) (n,dmodel)。
之前我们只讨论了 q q q 的形状应当是 ( h , n , d h e a d ) (h,n,d_{head}) (h,n,dhead),但并没有讨论它是如何变换得来的。这是因为, Q Q Q 在经过投影后得到的 q q q 只具有 ( n , d m o d e l ) (n,d_{model}) (n,dmodel) 的形状,要进行形状变换,一种做法是对 q q q 沿纵向切 h h h 刀再堆叠起来,这样从直观上来看也比较符合公式 ( 1 ) (1) (1)
q = torch.randn(n, d_model)
q = torch.stack(torch.split(q, d_head, dim=-1), dim=0)
但由于 W Q W^Q WQ 初始时是随机的,所以我们不需要严格按照公式 ( 1 ) (1) (1) 那样操作,直接执行 ( 2 ) (2) (2) 的逆变换即可
( n , d m o d e l ) = ( n , h ⋅ d h e a d ) → ( n , h , d h e a d ) → ( h , n , d h e a d ) (n,d_{model})=(n,h\cdot d_{head})\to(n,h,d_{head})\to(h,n,d_{head}) (n,dmodel)=(n,h⋅dhead)→(n,h,dhead)→(h,n,dhead)
现考虑有batch的情形,设批量大小为 b b b,则 Q Q Q 的形状为 ( b , n , d m o d e l ) (b,n,d_{model}) (b,n,dmodel) 或 ( n , b , d m o d e l ) (n,b,d_{model}) (n,b,dmodel),具体是哪一个要看 batch_first 是否为 True。接下来均假设 batch_first = False。
在以上的假设下, q q q 的形状也为 ( n , b , d m o d e l ) (n,b,d_{model}) (n,b,dmodel),我们将 b b b 和 h h h 看成同一维度(都是批量维),从而 ( 2 ) (2) (2) 式改写为
( n , b , d m o d e l ) → ( n , b , h , d h e a d ) → ( n , b ⋅ h , d h e a d ) → ( b ⋅ h , n , d h e a d ) (n,b,d_{model})\to(n,b,h,d_{head})\to(n,b\cdot h,d_{head})\to(b\cdot h,n,d_{head}) (n,b,dmodel)→(n,b,h,dhead)→(n,b⋅h,dhead)→(b⋅h,n,dhead)
关于 key_padding_mask 和 attn_mask 这里不再介绍,如有需要可阅读博主之前的文章,这里主要讲解如何合并两种mask。
前者的形状为 ( b , m ) (b,m) (b,m),用来mask掉key中的 [PAD],防止query注意到它。而后者的形状可以是 ( n , m ) (n,m) (n,m) 也可以是 ( b ⋅ h , n , m ) (b\cdot h,n,m) (b⋅h,n,m)。在实际合并两种mask的时候,我们均需要按照 ( b ⋅ h , n , m ) (b\cdot h,n,m) (b⋅h,n,m) 这个形状去计算。也就是说,如果是 key_padding_mask,我们需要进行形状变换 ( b , m ) → ( b , 1 , 1 , m ) → ( b , h , 1 , m ) → ( b ⋅ h , 1 , m ) (b,m)\to(b,1,1,m)\to(b,h,1,m)\to(b\cdot h,1,m) (b,m)→(b,1,1,m)→(b,h,1,m)→(b⋅h,1,m);如果是 attn_mask,我们需要进行形状变换 ( n , m ) → ( 1 , n , m ) (n,m)\to(1,n,m) (n,m)→(1,n,m)。
1.2 源码
本节将遵循以下记号:
| 记号 | 说明 |
|---|---|
| b b b | batch size |
| h h h | num heads |
| d d d | head dim |
| n n n | num queries |
| m m m | num key-value pairs |
首先实现一个MHA的基类:
class MultiheadAttentionBase_(nn.Module):def __init__(self, embed_dim, num_heads, dropout=0., bias=True):super().__init__()self.embed_dim = embed_dimself.num_heads = num_headsself.dropout = dropoutself.head_dim = embed_dim // num_headsassert self.head_dim * num_heads == embed_dimself.in_proj_weight = nn.Parameter(torch.empty(3 * embed_dim, embed_dim))if bias:self.in_proj_bias = nn.Parameter(torch.empty(3 * embed_dim))else:self.register_parameter('in_proj_bias', None)self.out_proj = nn.Linear(embed_dim, embed_dim, bias=bias)self._reset_parameters()def _reset_parameters(self):nn.init.xavier_uniform_(self.in_proj_weight)if self.in_proj_bias is not None:nn.init.constant_(self.in_proj_bias, 0.)nn.init.constant_(self.out_proj.bias, 0.)def forward(self,query,key,value,key_padding_mask,attn_mask,need_weights=True,):"""Args:query: (n, b, h * d)key: (m, b, h * d)value: (m, b, h * d)key_padding_mask: (b, m), bool typeattn_mask: (n, m) or (b * h, n, m), bool typeReturns:attn_output: (n, b, h * d)attn_weights: (b, h, n, m)"""w_q, w_k, w_v = self.in_proj_weight.chunk(3)if self.in_proj_bias is not None:b_q, b_k, b_v = self.in_proj_bias.chunk(3)else:b_q = b_k = b_v = Noneq = F.linear(query, w_q, b_q)k = F.linear(key, w_k, b_k)v = F.linear(value, w_v, b_v)b, h, d = q.size(1), self.num_heads, self.head_dimq, k, v = map(lambda x: x.reshape(-1, b, h, d), [q, k, v])attn_mask = self.merge_masks(key_padding_mask, attn_mask, q)attn_output, attn_weights = self.attention(q, k, v, attn_mask, out_proj=self.out_proj, dropout=self.dropout, training=self.training)if not need_weights:attn_weights = Nonereturn attn_output, attn_weightsdef merge_masks(self, key_padding_mask, attn_mask, q):"""Args:key_padding_mask: (b, m), bool typeattn_mask: (n, m) or (b * h, n, m), bool typeq: only used to confirm the dtype of attn_maskReturns:attn_mask: (b * h, n, m), float type"""assert key_padding_mask is not None and key_padding_mask.dtype == torch.boolb, m = key_padding_mask.size()key_padding_mask = key_padding_mask.view(b, 1, 1, m).expand(-1, self.num_heads, -1, -1).reshape(b * self.num_heads, 1, m)if attn_mask is not None:assert attn_mask.dtype == torch.boolif attn_mask.dim() == 2:attn_mask = attn_mask.unsqueeze(0)attn_mask = attn_mask.logical_or(key_padding_mask)else:attn_mask = key_padding_maskattn_mask = torch.zeros_like(attn_mask, dtype=q.dtype).masked_fill_(attn_mask, -1e28)return attn_maskdef attention(self, q, k, v, attn_mask, out_proj, dropout, training):"""Args:q: (n, b, h, d)k: (m, b, h, d)v: (m, b, h, d)attn_mask: (b * h, n, m), float typeout_proj: nn.Linear(h * d, h * d)Returns:attn_output: (n, b, h * d), is the result of concating h heads.attn_weights: (b, h, n, m)"""raise NotImplementedError
接下来,只需要重写 attention 方法就可以实现普通版的MHA了
class MultiheadAttention(MultiheadAttentionBase_):def attention(self, q, k, v, attn_mask, out_proj, dropout, training):if not training:dropout = 0n, b, h, d = q.size()q, k, v = map(lambda x: x.reshape(-1, b * h, d).transpose(0, 1), [q, k, v])attn_logits = q @ k.transpose(-2, -1) / math.sqrt(d) + attn_maskattn_probs = F.softmax(attn_logits, dim=-1)attn_weights = F.dropout(attn_probs, p=dropout)attn_output = attn_weights @ vattn_output = attn_output.transpose(0, 1).reshape(n, b, h * d)attn_output = out_proj(attn_output)return attn_output, attn_weights
1.3 极简版MHA(面试用)
不少面试会让现场手写MHA,这里提供了一份模版,略去了很多细节。
相比原版,极简版做了如下改动:
- 略去了参数初始化。
- 去掉了mask
class MultiheadAttention(nn.Module):def __init__(self, embed_dim, num_heads, dropout=0., bias=True):super().__init__()self.embed_dim = embed_dimself.num_heads = num_headsself.dropout = nn.Dropout(dropout)self.head_dim = embed_dim // num_headsassert self.head_dim * num_heads == embed_dimself.in_proj_weight = nn.Parameter(torch.empty(3 * embed_dim, embed_dim))if bias:self.in_proj_bias = nn.Parameter(torch.empty(3 * embed_dim))else:self.register_parameter('in_proj_bias', None)self.out_proj = nn.Linear(embed_dim, embed_dim, bias=bias)def forward(self, query, key, value):"""Args:query: (n, b, h * d)key: (m, b, h * d)value: (m, b, h * d)"""w_q, w_k, w_v = self.in_proj_weight.chunk(3)if self.in_proj_bias is not None:b_q, b_k, b_v = self.in_proj_bias.chunk(3)else:b_q = b_k = b_v = Noneq, k, v = F.linear(query, w_q, b_q), F.linear(key, w_k, b_k), F.linear(value, w_v, b_v)b, h, d = q.size(1), self.num_heads, self.head_dimq, k, v = map(lambda x: x.reshape(-1, b * h, d).transpose(0, 1), [q, k, v])attn_logits = q @ k.transpose(-2, -1) / math.sqrt(d)attn_probs = F.softmax(attn_logits, dim=-1)attn_weights = self.dropout(attn_probs)attn_output = attn_weights @ vattn_output = attn_output.transpose(0, 1).reshape(-1, b, h * d)attn_output = self.out_proj(attn_output)return attn_output, attn_weights
注意,如果尝试直接输出的话,会得到一堆 nan,这是因为没有xavier初始化,需要 _reset_parameters() 一下。
具体需要哪种mask可根据面试官的要求去实现。
2. Transformer
接下来基于PyTorch官方的MHA来实现Transformer。
首先需要实现一个基础函数,它可以用来复制一个 Module N次。
def _get_clones(module, n):return nn.ModuleList([copy.deepcopy(module) for _ in range(n)])
EncoderLayer的实现
class TransformerEncoderLayer(nn.Module):def __init__(self,d_model,n_head,d_ffn,dropout=0.1,activation=F.relu,norm_first=False,):super().__init__()self.self_attn = nn.MultiheadAttention(embed_dim=d_model, num_heads=n_head, dropout=dropout)self.dropout1 = nn.Dropout(dropout)self.linear1 = nn.Linear(d_model, d_ffn)self.activation = activationself.dropout2 = nn.Dropout(dropout)self.linear2 = nn.Linear(d_ffn, d_model)self.dropout3 = nn.Dropout(dropout)self.norm1 = nn.LayerNorm(d_model)self.norm2 = nn.LayerNorm(d_model)self.norm_first = norm_firstdef forward(self, src, src_mask, src_key_padding_mask):x = srcif self.norm_first:x = x + self._sa_block(self.norm1(x), src_mask, src_key_padding_mask)x = x + self._ff_block(self.norm2(x))else:x = self.norm1(x + self._sa_block(x, src_mask, src_key_padding_mask))x = self.norm2(x + self._ff_block(x))return xdef _sa_block(self, x, attn_mask, key_padding_mask):x = self.self_attn(x, x, x, attn_mask=attn_mask, key_padding_mask=key_padding_mask, need_weights=False)[0]return self.dropout1(x)def _ff_block(self, x):x = self.linear2(self.dropout2(self.activation(self.linear1(x))))return self.dropout3(x)
这里的 norm_first 用来决定是Pre-LN还是Post-LN,如下图所示
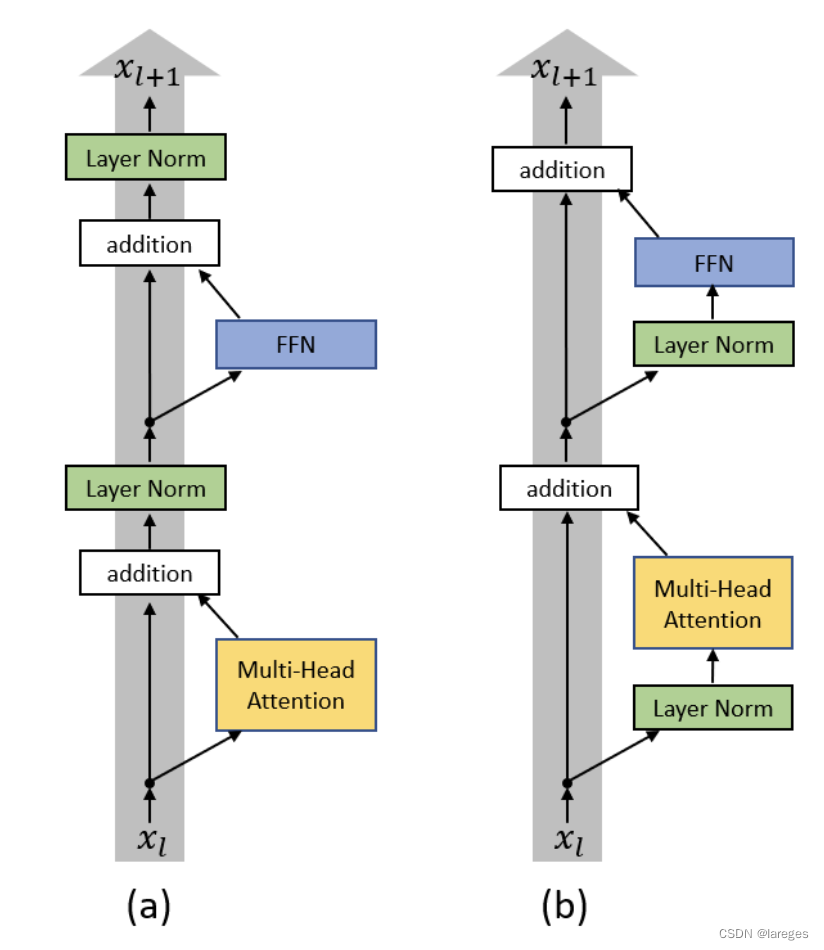
DecoderLayer的实现
class TransformerDecoderLayer(nn.Module):def __init__(self,d_model,n_head,d_ffn,dropout=0.1,activation=F.relu,norm_first=False,):super().__init__()self.self_attn = nn.MultiheadAttention(embed_dim=d_model, num_heads=n_head, dropout=dropout)self.dropout1 = nn.Dropout(dropout)self.cross_attn = nn.MultiheadAttention(embed_dim=d_model, num_heads=n_head, dropout=dropout)self.dropout2 = nn.Dropout(dropout)self.linear1 = nn.Linear(d_model, d_ffn)self.activation = activationself.dropout3 = nn.Dropout(dropout)self.linear2 = nn.Linear(d_ffn, d_model)self.dropout4 = nn.Dropout(dropout)self.norm1 = nn.LayerNorm(d_model)self.norm2 = nn.LayerNorm(d_model)self.norm3 = nn.LayerNorm(d_model)self.norm_first = norm_firstdef forward(self, tgt, memory, tgt_mask, memory_mask, tgt_key_padding_mask, memory_key_padding_mask):x = tgtif self.norm_first:x = x + self._sa_block(self.norm1(x), tgt_mask, tgt_key_padding_mask)x = x + self._ca_block(self.norm2(x), memory, memory_mask, memory_key_padding_mask)x = x + self._ff_block(self.norm3(x))else:x = self.norm1(x + self._sa_block(x, tgt_mask, tgt_key_padding_mask))x = self.norm2(x + self._ca_block(x, memory, memory_mask, memory_key_padding_mask))x = self.norm3(x + self._ff_block(x))return xdef _sa_block(self, x, attn_mask, key_padding_mask):x = self.self_attn(x, x, x, attn_mask=attn_mask, key_padding_mask=key_padding_mask, need_weights=False)[0]return self.dropout1(x)def _ca_block(self, x, mem, attn_mask, key_padding_mask):x = self.cross_attn(x, mem, mem, attn_mask=attn_mask, key_padding_mask=key_padding_mask, need_weights=False)[0]return self.dropout2(x)def _ff_block(self, x):x = self.linear2(self.dropout3(self.activation(self.linear1(x))))return self.dropout4(x)
根据EncoderLayer搭建Encoder。需要注意的是,PyTorch源码中还提供了 encoder_norm 这一参数,即决定是否在Encoder最后放一个LN。
class TransformerEncoder(nn.Module):def __init__(self, encoder_layer, num_layers, encoder_norm=None):super().__init__()self.layers = _get_clones(encoder_layer, num_layers)self.num_layers = num_layersself.encoder_norm = encoder_normdef forward(self, src, src_mask, src_key_padding_mask):output = srcfor mod in self.layers:output = mod(output, src_mask, src_key_padding_mask)if self.encoder_norm is not None:output = self.encoder_norm(output)return output
DecoderLayer同理
class TransformerDecoder(nn.Module):def __init__(self, decoder_layer, num_layers, decoder_norm=None):super().__init__()self.layers = _get_clones(decoder_layer, num_layers)self.num_layers = num_layersself.decoder_norm = decoder_normdef forward(self, tgt, memory, tgt_mask, memory_mask, tgt_key_padding_mask, memory_key_padding_mask):output = tgtfor mod in self.layers:output = mod(output, memory, tgt_mask, memory_mask, tgt_key_padding_mask, memory_key_padding_mask)if self.decoder_norm is not None:output = self.decoder_norm(output)return output
PyTorch官方的Transformer默认添加 encoder_norm 和 decoder_norm,然而这对于Post-LN的情形,无疑是多余的,所以这里我们做个简单修改,即如果是Post-LN情形,就不在最后添加LN了。
class Transformer(nn.Module):def __init__(self,d_model=512,n_head=8,num_encoder_layers=6,num_decoder_layers=6,d_ffn=2048,dropout=0.1,activation=F.relu,norm_first=False,):super().__init__()if norm_first:encoder_norm, decoder_norm = nn.LayerNorm(d_model), nn.LayerNorm(d_model)else:encoder_norm = decoder_norm = Noneencoder_layer = TransformerEncoderLayer(d_model, n_head, d_ffn, dropout, activation, norm_first)self.encoder = TransformerEncoder(encoder_layer, num_encoder_layers, encoder_norm)decoder_layer = TransformerDecoderLayer(d_model, n_head, d_ffn, dropout, activation, norm_first)self.decoder = TransformerDecoder(decoder_layer, num_decoder_layers, decoder_norm)self._reset_parameters()def _reset_parameters(self):for p in self.parameters():if p.dim() > 1:nn.init.xavier_uniform_(p)def forward(self,src,tgt,src_mask=None,tgt_mask=None,memory_mask=None,src_key_padding_mask=None,tgt_key_padding_mask=None,memory_key_padding_mask=None,):memory = self.encoder(src, src_mask, src_key_padding_mask)output = self.decoder(tgt, memory, tgt_mask, memory_mask, tgt_key_padding_mask, memory_key_padding_mask)return output
截止到目前,我们实现的Transfomer并不是完整的,还缺少embedding层和Decoder后面的Linear层,这里只介绍前者,因为后者仅仅是简单的 nn.Linear(d_model, tgt_vocab_size)。
Transformer的embedding层分为token embedding和Positional Encoding,前者是可学习的 nn.Embedding,后者是固定的Sinusoidal编码。
PE的公式为
P [ i , 2 j ] = sin ( i 1000 0 2 j / d m o d e l ) P [ i , 2 j + 1 ] = cos ( i 1000 0 2 j / d m o d e l ) 0 ≤ i < m a x _ l e n , 0 ≤ j < d m o d e l P[i,2j]=\sin\left(\frac{i}{10000^{2j/d_{model}}}\right)\\ P[i,2j+1]=\cos\left(\frac{i}{10000^{2j/d_{model}}}\right) \\ 0\leq i < max\_len,\;0\leq j<d_{model} P[i,2j]=sin(100002j/dmodeli)P[i,2j+1]=cos(100002j/dmodeli)0≤i<max_len,0≤j<dmodel
class PositionalEncoding(nn.Module):def __init__(self, d_model, dropout=0.1, max_len=5000):super().__init__()self.dropout = nn.Dropout(dropout)position = torch.arange(max_len).unsqueeze(1)div_term = torch.exp(torch.arange(0, d_model, 2) * (-math.log(10000.0) / d_model))pe = torch.zeros(max_len, 1, d_model) # 1是batch size维度pe[:, 0, 0::2] = torch.sin(position * div_term)pe[:, 0, 1::2] = torch.cos(position * div_term)self.register_buffer('pe', pe)def forward(self, x):x = x + self.pe[:x.size(0)]return self.dropout(x)
3. Q&A
1. MHA的参数量?FLOPs?时间复杂度?
只考虑自注意力情形。为简便起见,令 h ≜ d m o d e l h\triangleq d_{model} h≜dmodel。
MHA模块一共包含四个参数矩阵: W Q , W K , W V , W O W^Q,W^K,W^V,W^O WQ,WK,WV,WO,形状均为 ( h , h ) (h,h) (h,h),因此weight部分的参数量是 4 ⋅ h 2 4\cdot h^2 4⋅h2。每个参数矩阵都会带有一个长度为 h h h 的bias,因此总共的参数量为 4 h 2 + 4 h 4h^2+4h 4h2+4h。
📝 注意FLOPs和FLOPS的含义不同。前者是floating point operations,指浮点运算数,可以理解为计算量,用来衡量模型/算法的复杂度;后者是floating point operations per second,指每秒浮点运算次数,可以理解为计算速度,用来衡量衡量硬件的性能。
在计算形状为 ( m , n ) (m,n) (m,n) 和 ( n , k ) (n,k) (n,k) 矩阵的乘积时,每计算一次内积都要执行 n n n 次乘法和 n n n 次加法,而最终输出矩阵的形状为 ( m , k ) (m,k) (m,k),所以总共的浮点运算次数为 ( n + n ) ⋅ m ⋅ k = 2 m n k (n+n)\cdot m\cdot k=2mnk (n+n)⋅m⋅k=2mnk。
回到MHA,只考虑矩阵乘法:
- 首先会对形状为 ( l , b , h ) (l,b,h) (l,b,h) 的embedding进行投影,执行的矩阵乘法为 ( l , b , h ) × ( h , h ) → ( l , b , h ) (l,b,h)\times (h, h)\to(l,b,h) (l,b,h)×(h,h)→(l,b,h),这一步的计算量为 2 l b h 2 2lbh^2 2lbh2。由于会分别投影到 Q , K , V Q,K,V Q,K,V 三个矩阵,因此这一步的总计算量为 6 l b h 2 6lbh^2 6lbh2。
- 接下来是 Q K T QK^T QKT 相乘,执行的矩阵乘法为 ( b ⋅ n h , l , h d ) × ( b ⋅ n h , h d , l ) → ( b ⋅ n h , l , l ) (b\cdot nh,l,hd)\times(b\cdot nh,hd,l)\to(b\cdot nh,l,l) (b⋅nh,l,hd)×(b⋅nh,hd,l)→(b⋅nh,l,l),其中 n h nh nh 代表
num_heads, h d hd hd 代表head_dim。计算量为 2 l 2 b h 2l^2bh 2l2bh。 - 然后是对 V V V 进行加权,执行的矩阵乘法为 ( b ⋅ n h , l , l ) × ( b ⋅ n h , l , h d ) → ( b ⋅ n h , l , h d ) (b\cdot nh,l,l)\times(b\cdot nh,l,hd)\to(b\cdot nh,l,hd) (b⋅nh,l,l)×(b⋅nh,l,hd)→(b⋅nh,l,hd),计算量为 2 l 2 b h 2l^2bh 2l2bh。
- 最后的投影中,执行的矩阵乘法为 ( l , b , h ) × ( h , h ) → ( l , b , h ) (l,b,h)\times(h,h)\to(l,b,h) (l,b,h)×(h,h)→(l,b,h),计算量为 2 l b h 2 2lbh^2 2lbh2。
由上述步骤可知,MHA的FLOPs约为 6 l b h 2 + 2 l 2 b h + 2 l 2 b h + 2 l b h 2 = 4 l b h ( 2 h + l ) 6lbh^2+2l^2bh+2l^2bh+2lbh^2=4lbh(2h+l) 6lbh2+2l2bh+2l2bh+2lbh2=4lbh(2h+l)。
再来看MHA的复杂度,依然只考虑矩阵乘法。在计算形状为 ( m , n ) (m,n) (m,n) 和 ( n , k ) (n,k) (n,k) 矩阵的乘积时,计算内积的时间复杂度为 O ( n ) O(n) O(n),而输出矩阵的形状为 ( m , k ) (m,k) (m,k),填满这个矩阵所需要的时间为 O ( m k ) O(mk) O(mk),所以总时间复杂度为 O ( m n k ) O(mnk) O(mnk)。
可以发现一个不严谨的等式(仅针对矩阵乘法场景):
时间复杂度 = O ( FLOPs 2 ) 时间复杂度=O\left(\frac{\text{FLOPs}}{2}\right) 时间复杂度=O(2FLOPs)
由此可得到MHA的时间复杂度为 O ( 2 l b h ( 2 h + l ) ) = O ( l b h 2 + l 2 b h ) O(2lbh(2h+l))=O(lbh^2+l^2bh) O(2lbh(2h+l))=O(lbh2+l2bh)。特别地,当 b = 1 b=1 b=1 时,MHA的时间复杂度退化为 O ( l h 2 + l 2 h ) O(lh^2+l^2h) O(lh2+l2h)。
注意,MHA和SA(Self-Attention)的时间复杂度不同,SA的复杂度为 O ( l 2 h ) O(l^2h) O(l2h)。对于Restricted SA,注意力矩阵的每一行仅有 r r r 个元素需要计算,因此总共需要 r l rl rl 个元素需要计算,而计算每个元素的时间为 O ( h ) O(h) O(h),所以总时间为 O ( r l h ) O(rlh) O(rlh)。
2. Transformer的总参数量?模型占用显存?
此前已经计算出MHA部分的参数量为 4 h 2 + 4 h 4h^2+4h 4h2+4h,接下来看FFN部分。FFN有两个参数矩阵,形状分别为 ( h , 4 h ) (h,4h) (h,4h) 和 ( 4 h , h ) (4h,h) (4h,h),伴随它们的是两个bias,分别为 ( 4 h , ) (4h,) (4h,) 和 ( h , ) (h,) (h,),因此FFN部分的总参数量为 8 h 2 + 5 h 8h^2+5h 8h2+5h。
事实上,LayerNorm模块也有参数量,LN含有两个参数 γ \gamma γ 和 β \beta β,这两个参数均以形状为 ( h , ) (h,) (h,) 的张量进行存储,所以LN总共的参数为 2 h 2h 2h。
截至目前,我们可以做一个小总结:
| 模块 | 参数量 |
|---|---|
| MHA | 4 h 2 + 4 h 4h^2+4h 4h2+4h |
| FFN | 8 h 2 + 5 h 8h^2+5h 8h2+5h |
| LN | 2 h 2h 2h |
下面假设 num_encoder_layers 和 num_decoder_layers 均为 n n n。
一个EncoderLayer包含一个MHA,一个FFN和两个LN,所以一个EncoderLayer的参数量为 4 h 2 + 4 h + 8 h 2 + 5 h + 2 h ⋅ 2 = 12 h 2 + 13 h 4h^2+4h+8h^2+5h+2h\cdot 2=12h^2+13h 4h2+4h+8h2+5h+2h⋅2=12h2+13h,整个Encoder的参数量为 n ( 12 h 2 + 13 h ) n(12h^2+13h) n(12h2+13h)。
一个DecoderLayer包含两个MHA,一个FFN和三个LN,所以一个DecoderLayer的参数量为 8 h 2 + 8 h + 8 h 2 + 5 h + 6 h = 16 h 2 + 19 h 8h^2+8h+8h^2+5h+6h=16h^2+19h 8h2+8h+8h2+5h+6h=16h2+19h,整个Decoder的参数量为 n ( 16 h 2 + 19 h ) n(16h^2+19h) n(16h2+19h)。
由于PyTorch官方实现的Transformer还会默认增加 encoder_norm 和 decoder_norm,所以算上这两个LN,我们可以得到Transformer核心架构的参数量为 n ( 12 h 2 + 13 h ) + n ( 16 h 2 + 19 h ) + 2 h ⋅ 2 = n ( 28 h 2 + 32 h ) + 4 h n(12h^2+13h)+n(16h^2+19h)+2h\cdot 2=n(28h^2+32h)+4h n(12h2+13h)+n(16h2+19h)+2h⋅2=n(28h2+32h)+4h。将 n = 6 , h = 512 n=6,h=512 n=6,h=512 代入可得 6 ( 28 ⋅ 51 2 2 + 32 ⋅ 512 ) + 512 ⋅ 4 = 44140544 6(28\cdot 512^2+32\cdot 512)+512\cdot 4=44140544 6(28⋅5122+32⋅512)+512⋅4=44140544,该结果与下述代码的输出相同,这也验证了我们计算的正确性。
model = torch.nn.Transformer()
print(sum([p.numel() for p in model.parameters()]))
需要注意,上面提到了核心架构四个字,这是因为截至目前我们并没有计算出完整的Transformer的参数量。完整的Transformer除了核心架构外还应当包含Token Embedding和Decoder最后的线性层(即应当包含所有可学习的参数)。
假设Encoder和Decoder共用一个词表,且词表大小为 V V V,那么完整的Transformer的总参数量应当为
n ( 28 h 2 + 32 h ) + 4 h ⏟ 核心架构 + V ⋅ h ⏟ 词嵌入矩阵 + h ⋅ V ⏟ 输出层 = n ( 28 h 2 + 32 h ) + ( 4 + 2 V ) h \underbrace{n(28h^2+32h)+4h}_{核心架构}+\underbrace{V\cdot h}_{词嵌入矩阵}+\underbrace{h\cdot V}_{输出层}=n(28h^2+32h)+(4+2V)h 核心架构 n(28h2+32h)+4h+词嵌入矩阵 V⋅h+输出层 h⋅V=n(28h2+32h)+(4+2V)h
由于 V V V 要根据具体的数据集来确定,所以接下来我们只关心核心架构占用的显存。
PyTorch的Transformer的参数均以float32进行存储,一个浮点数占 4 4 4 个字节,那么核心架构总共占 44140544 ⋅ 4 / 102 4 2 ≈ 168 44140544\cdot4/1024^2\approx168 44140544⋅4/10242≈168 MB。由此可以看出,占用显存的大头其实还是数据,模型本身并不会占用太多。
3. Transformer的FLOPs?
此前已经得出MHA的FLOPs为 4 l b h ( 2 h + l ) 4lbh(2h+l) 4lbh(2h+l),接下来看FFN部分,我们依然只关心矩阵乘法。
显而易见,FFN部分会经历两次矩阵乘法:
- 第一次: ( l , b , h ) × ( h , 4 h ) → ( l , b , 4 h ) (l,b,h)\times(h,4h)\to(l,b,4h) (l,b,h)×(h,4h)→(l,b,4h),这一步的计算量为 8 l b h 2 8lbh^2 8lbh2;
- 第二次: ( l , b , 4 h ) × ( 4 h , h ) → ( l , b , h ) (l,b,4h)\times(4h,h)\to(l,b,h) (l,b,4h)×(4h,h)→(l,b,h),这一步的计算量为 8 l b h 2 8lbh^2 8lbh2;
LN部分不涉及矩阵乘法,Embedding部分仅仅是查表,也不涉及矩阵乘法,最后的输出层(计算logits)会涉及,即 ( l , b , h ) × ( h , V ) → ( l , b , V ) (l,b,h)\times(h,V)\to(l,b,V) (l,b,h)×(h,V)→(l,b,V),计算量 2 l b h V 2lbhV 2lbhV。
截至目前,我们可以做一个小总结:
| 模块 | FLOPs |
|---|---|
| MHA | 4 l b h ( 2 h + l ) 4lbh(2h+l) 4lbh(2h+l) |
| FFN | 16 l b h 2 16lbh^2 16lbh2 |
| Output | 2 l b h V 2lbhV 2lbhV |
由此可知,Encoder部分的FLOPs为 n ( 4 l b h ( 2 h + l ) + 16 l b h 2 ) = 4 n l b h ( 6 h + l ) n(4lbh(2h+l)+16lbh^2)=4nlbh(6h+l) n(4lbh(2h+l)+16lbh2)=4nlbh(6h+l),Decoder部分的FLOPs为 n ( 8 l b h ( 2 h + l ) + 16 l b h 2 ) = 8 n l b h ( 4 h + l ) n(8lbh(2h+l)+16lbh^2)=8nlbh(4h+l) n(8lbh(2h+l)+16lbh2)=8nlbh(4h+l),所以整个Transformer的FLOPs为
4 n l b h ( 6 h + l ) + 8 n l b h ( 4 h + l ) + 2 l b h V = 4 n l b h ( 14 h + 3 l ) + 2 l b h V 4nlbh(6h+l)+8nlbh(4h+l)+2lbhV=4nlbh(14h+3l)+2lbhV 4nlbh(6h+l)+8nlbh(4h+l)+2lbhV=4nlbh(14h+3l)+2lbhV
需要注意的是,虽然Embedding部分没有FLOPs,但仍可以计算它的时间复杂度。初始时,数据的形状为 ( b , l ) (b,l) (b,l),其中的每个元素都对应了token在vocab中的索引,通过该索引查表的时间复杂度为 O ( 1 ) O(1) O(1),因此嵌入过程 ( b , l ) → ( b , l , h ) (b,l)\to(b,l,h) (b,l)→(b,l,h) 的时间复杂度为 O ( l b ) O(lb) O(lb)。
同理可计算LN的时间复杂度。在对形状为 ( l , b , h ) (l,b,h) (l,b,h) 的张量进行LN时,LN会首先计算最后一个维度上的均值和方差,再对最后一个维度进行归一化处理,下面是一个简易版的LN
def layer_norm(x):"""Args:x: (l, b, h)"""x_mean = torch.mean(x, dim=-1, keepdim=True)x_std = torch.std(x, dim=-1, unbiased=False, keepdim=True) # 这里要使用有偏标准差return (x - x_mean) / x_std
显然LN的时间复杂度为 O ( l b h ) O(lbh) O(lbh)。
4. 参数量、FLOPs、时间复杂度汇总
| 模块 | 参数量 | FLOPs(只考虑矩阵乘法) | 时间复杂度(不考虑批量) |
|---|---|---|---|
| MHA | 4 h 2 + 4 h 4h^2+4h 4h2+4h | 4 l b h ( 2 h + l ) 4lbh(2h+l) 4lbh(2h+l) | O ( l h 2 + l 2 h ) O(lh^2+l^2h) O(lh2+l2h) |
| FFN | 8 h 2 + 5 h 8h^2+5h 8h2+5h | 16 l b h 2 16lbh^2 16lbh2 | O ( l h 2 ) O(lh^2) O(lh2) |
| LN | 2 h 2h 2h | —— | O ( l h ) O(lh) O(lh) |
| Encoder | n ( 12 h 2 + 13 h ) n(12h^2+13h) n(12h2+13h) | 4 n l b h ( 6 h + l ) 4nlbh(6h+l) 4nlbh(6h+l) | O ( n ( l h 2 + l 2 h ) ) O(n(lh^2+l^2h)) O(n(lh2+l2h)) |
| Decoder | n ( 16 h 2 + 19 h ) n(16h^2+19h) n(16h2+19h) | 8 n l b h ( 4 h + l ) 8nlbh(4h+l) 8nlbh(4h+l) | O ( n ( l h 2 + l 2 h ) ) O(n(lh^2+l^2h)) O(n(lh2+l2h)) |
| Transformer-Core | n ( 28 h 2 + 32 h ) + 4 h n(28h^2+32h)+4h n(28h2+32h)+4h | 4 n l b h ( 14 h + 3 l ) 4nlbh(14h+3l) 4nlbh(14h+3l) | O ( n ( l h 2 + l 2 h ) ) O(n(lh^2+l^2h)) O(n(lh2+l2h)) |
| Embedding | V h Vh Vh | —— | O ( l ) O(l) O(l) |
| Output | V h Vh Vh | 2 l b h V 2lbhV 2lbhV | O ( l h V ) O(lhV) O(lhV) |
| Transformer-Complete | n ( 28 h 2 + 32 h ) + ( 4 + 2 V ) h n(28h^2+32h)+(4+2V)h n(28h2+32h)+(4+2V)h | 4 n l b h ( 14 h + 3 l ) + 2 l b h V 4nlbh(14h+3l)+2lbhV 4nlbh(14h+3l)+2lbhV | O ( n ( l h 2 + l 2 h ) + l h V ) O(n(lh^2+l^2h)+lhV) O(n(lh2+l2h)+lhV) |
据此,可以总结出:
- 参数量方面: FFN > MHA > LN,且单个FFN的参数量约为单个MHA的两倍。Decoder参数量略大于Encoder的参数量。 在整个Transformer中,FFN占 57.1 % 57.1\% 57.1%,MHA占 42.8 % 42.8\% 42.8%,LN占 0.1 % 0.1\% 0.1%。
- 耗时方面: MHA > FFN > LN,Transformer的计算主要都花在了MHA上。
- 计算量方面: 在整个Transformer的FLOPs中,当 h < 3 2 l h<\frac{3}{2}l h<23l 时,MHA的占比超过FFN,否则相反。
🧑💻 如有错误欢迎在评论区指出!
Ref
[1] https://zhuanlan.zhihu.com/p/264749298
[2] https://zhuanlan.zhihu.com/p/624740065
相关文章:

重新审视MHA与Transformer
本文将基于PyTorch源码重新审视MultiheadAttention与Transformer。事实上,早在一年前博主就已经分别介绍了两者:各种注意力机制的PyTorch实现、从零开始手写一个Transformer,但当时的实现大部分是基于d2l教程的,这次将基于PyTorch…...
Docker 全栈体系(七)
Docker 体系(高级篇) 五、Docker-compose容器编排 1. 是什么 Compose 是 Docker 公司推出的一个工具软件,可以管理多个 Docker 容器组成一个应用。你需要定义一个 YAML 格式的配置文件docker-compose.yml,写好多个容器之间的调…...
【编程范式】聊聊什么是数据类型和范式的本质
什么是编程范式 范式其实就是做事的方式,编程范式可以理解为如何编程,按照什么样的模式或者风格进行编程。 编程范式包含哪些 泛型编程函数式编程面向对象编程编程本质和逻辑编程 虽然有不同的编程范式,但是对于目的来说都是为了解决同一…...
2023-08-01 python根据x轴、y轴坐标(数组)在坐标轴里画出曲线图,python 会调用鼎鼎大名的matlib,用来分析dac 数据
一、python 源码如下 import numpy as np import matplotlib as mpl import matplotlib.pyplot as plt#x[0 ,1,2,3,5,6,10] #y[0,0,3,4,5,7,8]# { 0 , 1 , 0x0003 },// 0 # { 0XFFFF * 1 / 10 , 3006 , 0x0a6b },// 1 # { 0XFFFF * 2 / 10 , 599…...
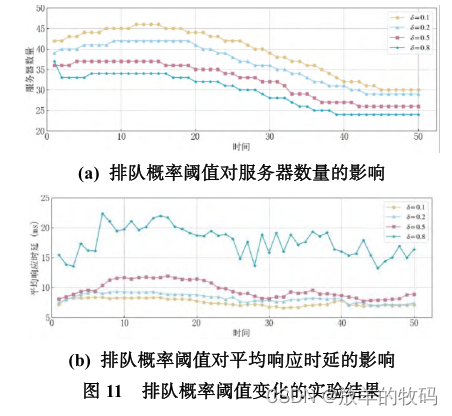
小研究 - 主动式微服务细粒度弹性缩放算法研究(四)
微服务架构已成为云数据中心的基本服务架构。但目前关于微服务系统弹性缩放的研究大多是基于服务或实例级别的水平缩放,忽略了能够充分利用单台服务器资源的细粒度垂直缩放,从而导致资源浪费。为此,本文设计了主动式微服务细粒度弹性缩放算法…...
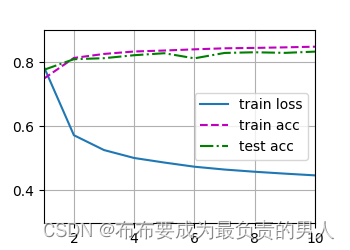
机器学习深度学习——softmax回归的简洁实现
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——softmax回归从零开始实现 📚订阅专栏:机器学习&&深度学习 希望文章对你…...
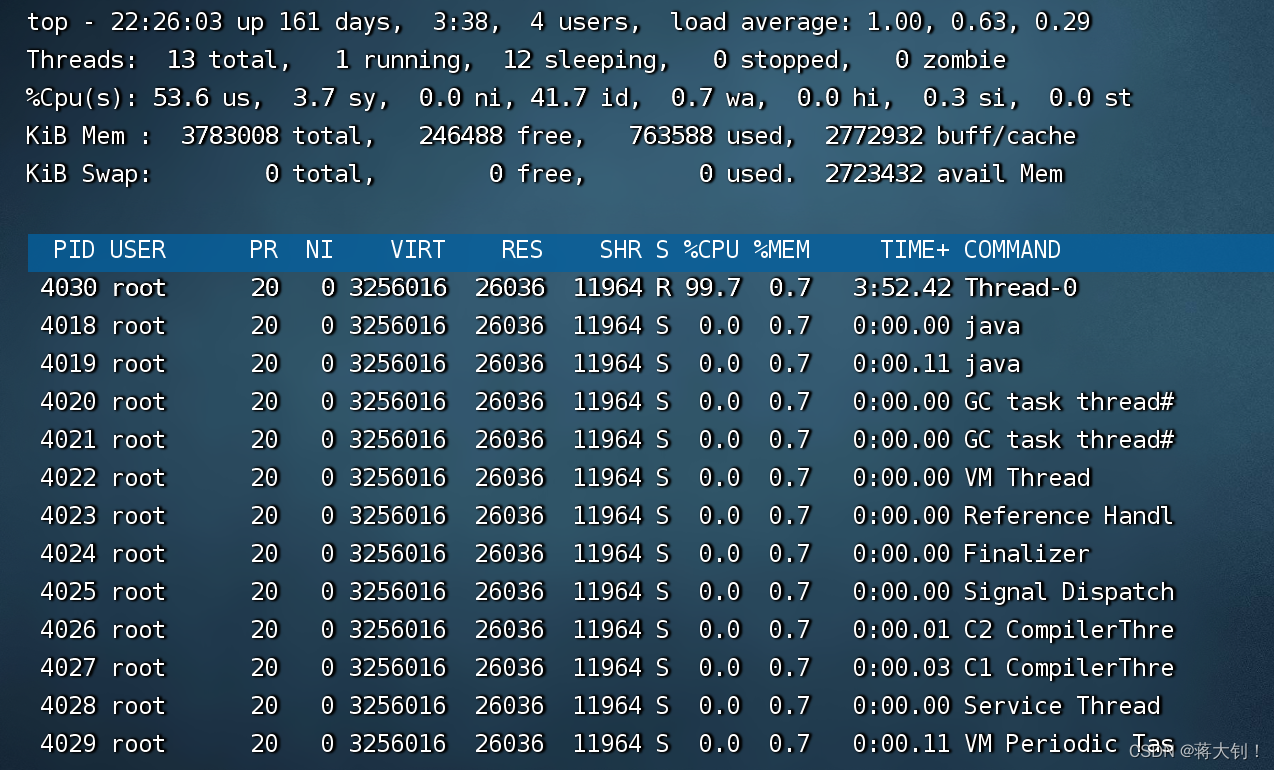
CPU利用率过高解决思路
文章目录 问题场景问题定位问题解决 本文参考: Linux服务器之CPU过高解决思路_linux cpu温度过高_Jeremy_Lee123的博客-CSDN博客 Java程序员必备:jstack命令解析 - 掘金 (juejin.cn) 重点问题!CPU利用率过高排查思路|原创 (qq.…...

Redis(三)—— Redis基本的事务操作、Redis实现乐观锁
一、Redis基本的事务操作 首先声明: redis的单条命令是保证原子性的(回想一下setnx k1 v1 k5 v5命令如果k1已经存在,那么k5也会设置失败)但是redis的事务不保证原子性!见下面“1.2 某条命令有错怎么办?”…...

SQLI_LABS攻击
目录 Less1 首先来爆字段 联合注入 判断注入点 爆数据库名 爆破表名 information_schema information_schmea.tables group_concat() 爆破列名 information_schema.columns 爆值 SQLMAP Less-2 -4 Less -5 布尔 数据库 表名 字段名 爆破值 SQLMAP Less-6 …...

如何查看 Chrome 网站有没有前端 JavaScript 报错?
您可以按照以下步骤在Chrome中查看网站是否存在前端JavaScript报错: 步骤1:打开Chrome浏览器并访问网站 首先,打开Chrome浏览器并访问您想要检查JavaScript报错的网站。 步骤2:打开开发者工具 在Chrome浏览器中,按…...
JS前端读取本地上传的File文件对象内容(包括Base64、text、JSON、Blob、ArrayBuffer等类型文件)
读取base64图片File file2Base64Image(file, cb) {const reader new FileReader();reader.readAsDataURL(file);reader.onload function (e) {cb && cb(e.target.result);//即为base64结果}; }, 读取text、JSON文件File readText(file, { onloadend } {}) {const re…...
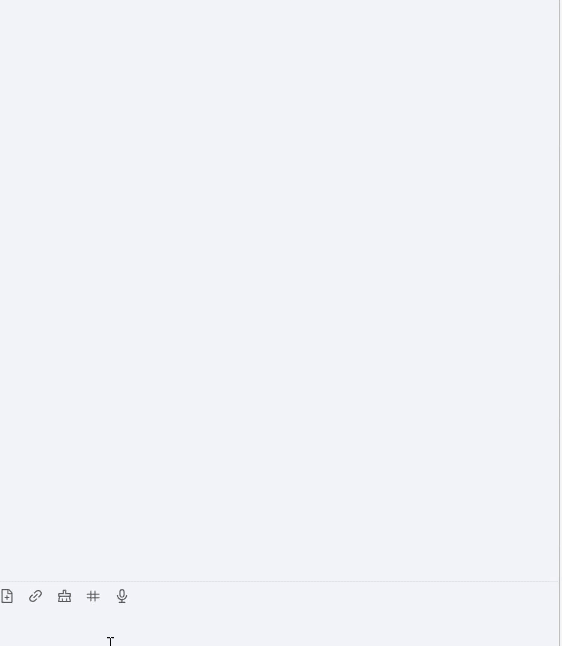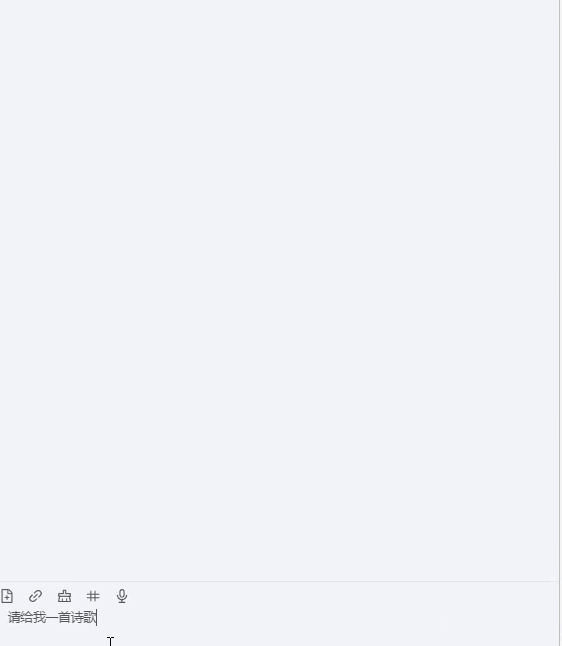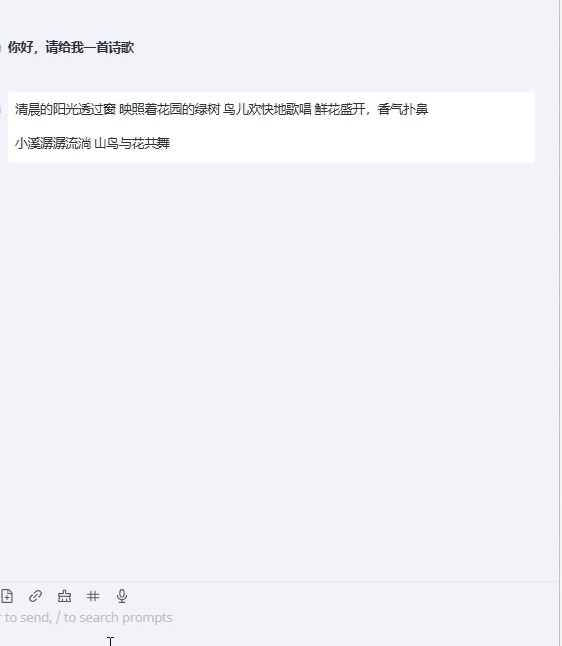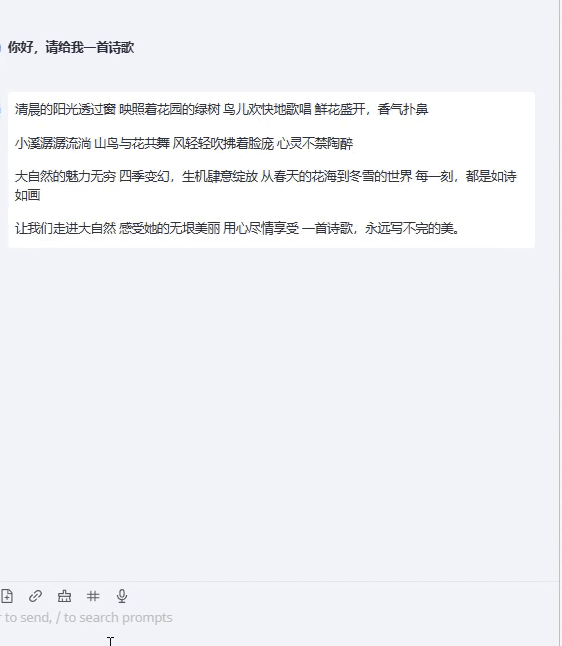
【项目方案】OpenAI流式请求实现方案
文章目录 实现目的效果比对非stream模式stream模式实现方案方案思路总体描述前端方案对比event-source-polyfill代码示例前端实现遇到的问题与解决方法后端参考资料时序图关键代码示例后端实现时遇到的问题与解决方法实现目的 stream是OpenAI API中的一个参数,用于控制请求的…...
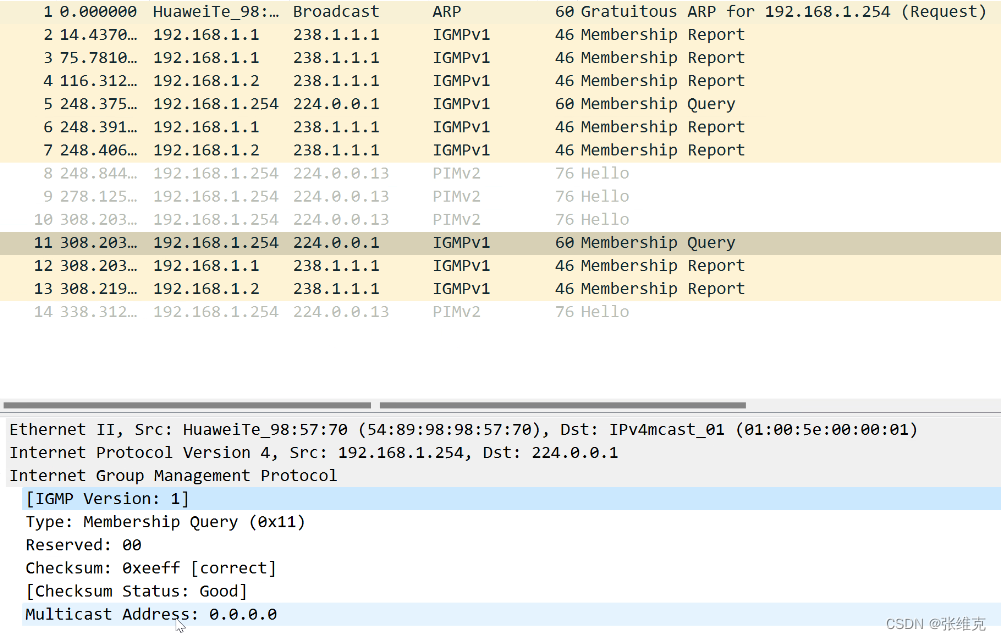
华为数通HCIP-IP组播基础
点到点业务:比如FTP,WEB业务,此类业务主要特点是不同的用户有不同的需求,比如用户A需要下载资料A,用户B需要下载资料B。此类业务一般由单播承载,服务器对于不同用户发送不同的点到点数据流。 ospf、isis…...

STM32 SPI学习
SPI 串行外设设备接口(Serial Peripheral Interface),是一种高速的,全双工,同步的通信总线。 SCK时钟信号由主机发出。 SPI接口主要应用在存储芯片。 SPI相关引脚:MOSI(输出数据线ÿ…...

分布式缓存与数据库的一致性记录
用户更新数据库,需要再去更新redis缓存,否则会造成缓存与数据库数据不一致 一致性的两种方法 1). 双写模式 更新完数据库之后,更新redis缓存数据 问题: 因为请求时间的问题,造成缓存数据不是最新的 数据。 原因:A先修…...

vue3的语法
main.js中写发生变化,并不兼容vue2的写法 //vue3 import { createApp } from vue import ./style.css import App from ./App.vuecreateApp(App).mount(#app)//vue2 import Vue from vue import ./style.css import App from ./App.vueconst vm new Vue({render:h…...

【git合并分支自定义提交消息】
开发分支 dev主分支 master 需求 dev分支开发完后合并到master分支自定义提交信息 通过 git merge dev --squash --no-commit此命令会拉取dev分支代码到当前分支,并不会自动提交,可以自己修改提交信息...
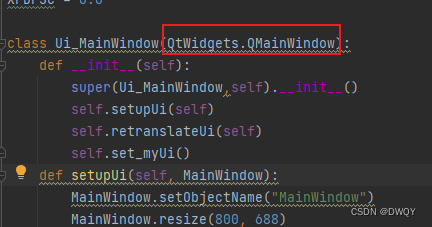
AttributeError: module ‘PyQt5.QtGui‘ has no attribute ‘QMainWindow‘
场景描述: 这个问题是使用PyUIC将ui文件变成py文件后遇到的 解决办法: 改动1:把object改成QtWidgets.QMainWindow 改动2:增加__init__函数,函数结构如下: def __init__(self):super(Ui_MainWindow,self).…...

基于Java+SpringBoot+Vue前后端分离电商项目
晚间lucky为友友们送福利啦~🎁 Tips:有需要毕业设计指导的童鞋一定要认真看哦,文末有彩蛋。 一.项目介绍 该电商项目是一个简单、入门级的电商项目,是基于JavaSpringBootVue前后端分离项目。前端采用两套独立的系统分别完成项目…...
实现思路)
Rpc服务消费者(Rpc服务调用者)实现思路
Rpc服务消费者(Rpc服务调用者)实现思路 前面几节说到Rpc消费者主要通过UserServiceRPc_Stub这个protobuf帮我们生成的类来实现,上代码回顾一下 class UserServiceRpc_Stub : public UserServiceRpc {public:UserServiceRpc_Stub(::PROTOBUF…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...
