java数据算法-汉诺塔
1、有三根相邻的柱子,标号为A,B,C。
2、A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘。
3、现在把所有盘子一个一个移动到柱子C上,并且每次移动同一根柱子上都不能出现大盘子在小盘子上方。
题解步骤
1、当n=1时;
将1号从A移动到C即可
2、当n=2时;
第一步:将1号从A移动到B
第二步:将2号从A移动到C
第三步:将1号从B移动到C
3、当n=3时;
第一步:将1号从A移动到C
第二步:将2号从A移动到B
第三步:将1号从C移动到B
第四步:将3号从A移动到C
第五步:将1号从B移动到A
第六步:将2号从B移动到C
第七步:将1号从A移动到C
......
由上述可以看出,每次都会有将最大的一个从A移动到C的步骤。假如有n(n>1)个需要移动的盘子,我们可以将这些步骤分为3步:
1、将1到n-1的盘子通过C的辅助从A移动到B
2、将第n个盘子移动到C
3、将1到n-1de盘子通过A辅助从B移动到C
由此我们可以想到用递归的方法。
/*** @see [相关类/方法](可选)* @since [产品/模块版本] (可选)*/
public class HanoiTower {public static void hanoi(int n, String a, String b,String c) {if (n == 1) {// 只有一个圆盘时直接从A石柱移动到C石柱move(n, a, c);} else {// 将前n-1个圆盘从石柱A移动到石柱Bhanoi(n - 1, a, c, b);// 将第n号圆盘从石柱A移动到石柱Cmove(n, a, c);// 将前n-1个圆盘从石柱B移动到石柱Chanoi(n - 1, b, a, c);}}public static void move(int n, String i, String j) {System.out.println("第" + n + "个圆盘," + "从" + i + "移动到" + j);}public static void main(String[] args) {hanoi(2,"A","B","C");}
}相关文章:

java数据算法-汉诺塔
1、有三根相邻的柱子,标号为A,B,C。 2、A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘。 3、现在把所有盘子一个一个移动到柱子C上,并且每次移动同一根柱子上都不能出现大盘子在小盘子上方。 题解步骤 1、当n1时; 将1号从A移动到C即…...

[QT编程系列-35]:数据存储 - JSON格式配置数据的存储与通知
目录 1. QJsonObject 2 QJsonDocument 3 JSON本文格式 4. JSON示例 5. JASON配置文件示例 1. QJsonObject QJsonObject 是Qt的类之一,用于表示 JSON 对象。 JSON(JavaScript Object Notation)是一种轻量级的数据交换格式࿰…...

【Spring】Spring 中事务的实现
目录 1.编程式事务(手动编写代码)2.声明式事务(利用注解)2.1 Transactional作用范围2.2 Transactional参数说明2.3 Transactional工作原理 3.Spring 中设置事务隔离级别3.1 事务四大特性ACID3.2 事务的隔离级别3.2 Spring中设置事…...
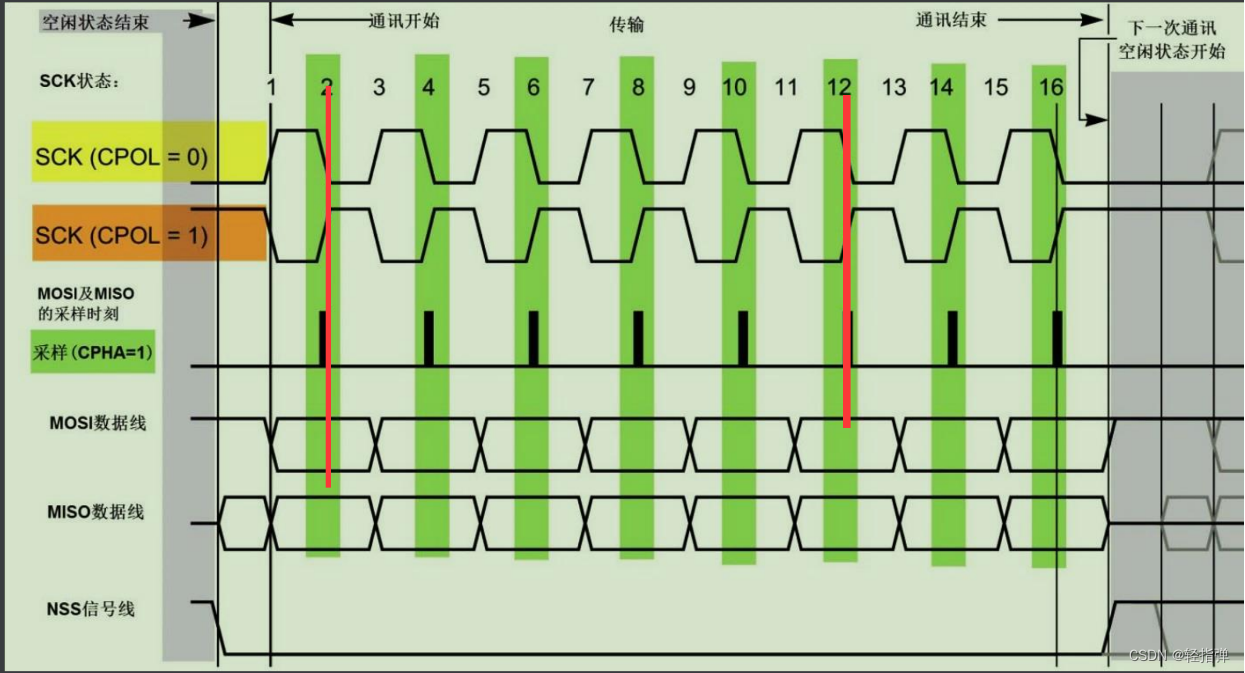
Linux 学习记录60(ARM篇)
Linux 学习记录60(ARM篇) 本文目录 Linux 学习记录60(ARM篇)一、SPI总线1. 概念2. 硬件连接 二、SPI总线协议三、SPI总线通信模式四、对比IIC总线和SPI总线1. 相同点2. 不同点 思维导图 一、SPI总线 1. 概念 1、SPI总结是Motorola首先提出的全双工三线/四线同步串行总线 2、采…...
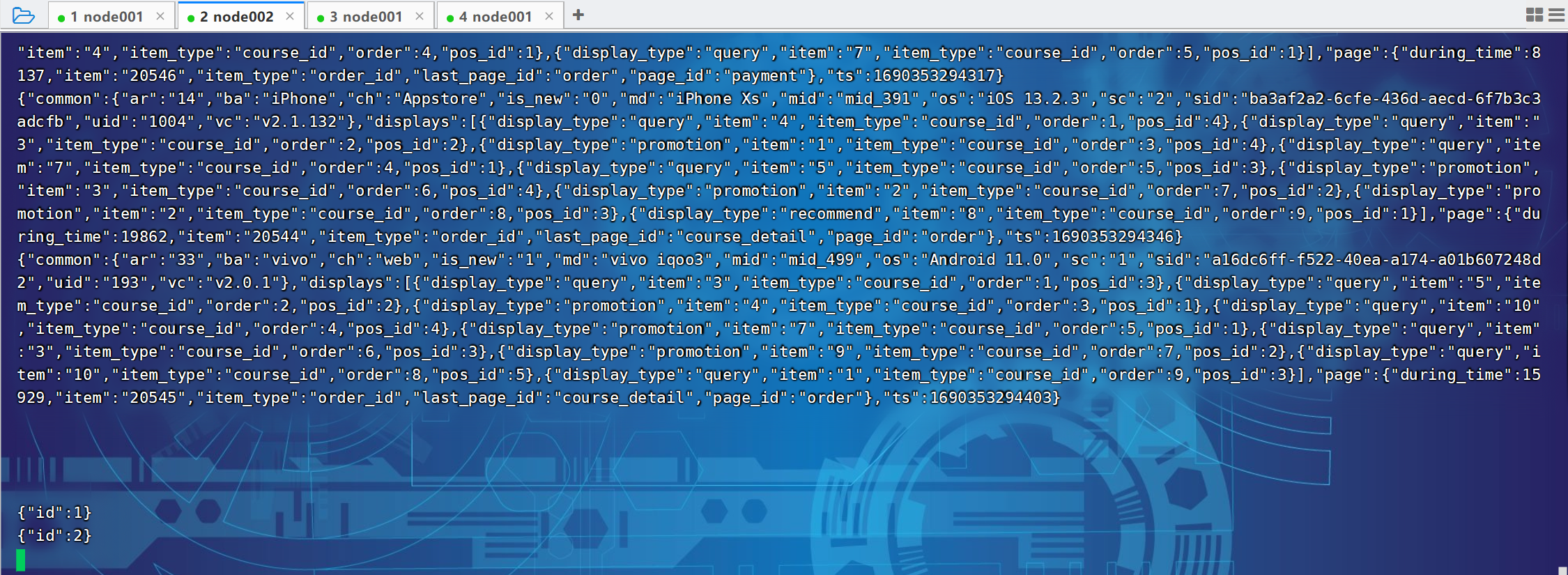
尚硅谷大数据项目《在线教育之采集系统》笔记002
视频地址:尚硅谷大数据项目《在线教育之采集系统》_哔哩哔哩_bilibili 目录 P032 P033 P033 P034 P035 P036 P032 P033 # 1、定义组件,为各组件命名 a1.sources r1 a1.channels c1 a1.sinks - k1# 2、配置sources,描述source a1.sour…...

校园跑腿小程序功能分享
提起校园跑腿小程序大家都不陌生,尤其是对上大学的伙伴们来说,更是熟悉得不能再熟悉了,和我们的生活息息相关,密不可分。 对于现在的年轻人来说,网购是非常简单和方便的一种购物方式,随之快递也会越来越多。在我们国家…...
PHP8的变量-PHP8知识详解
昨天我们讲解了PHP8的常量,今天讲解PHP8的变量。常量有定义常量和预定义常量,变量呢?那就没有定义变量了,那叫给变量赋值,但是还是有预定义变量的。下面就给大家讲解什么是变量、变量赋值及使用及预定义变量。 一、什么…...
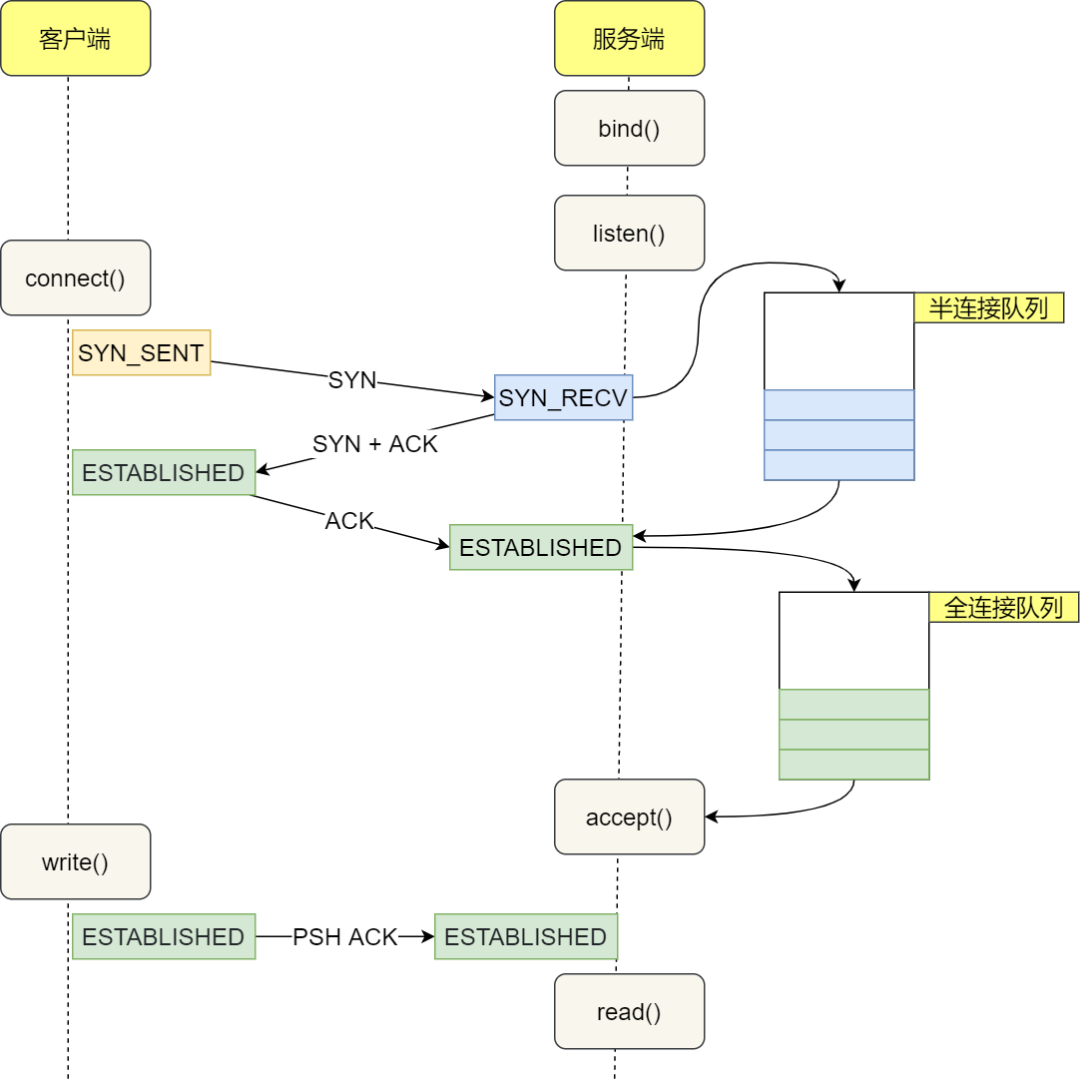
图解TCP 三次握手和四次挥手的高频面试题(2023最新版)
大家好,最近重新整理了一版 TCP 三次握手和四次挥手的面试题(2023最新版)。 ----- 任 TCP 虐我千百遍,我仍待 TCP 如初恋。 巨巨巨巨长的提纲,发车!发车! img TCP 基本认识 TCP 头格式有哪些…...
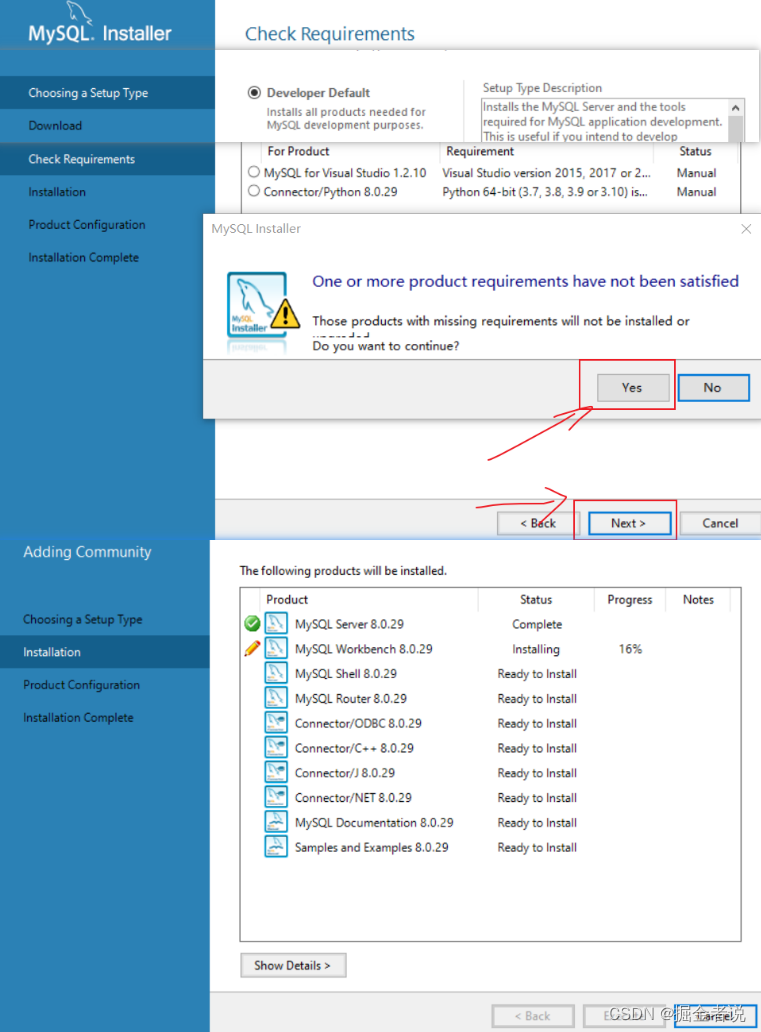
【mysql】Win10安装配置MySQL8.0简要
下载 MySQL官网下载安装包 安装...

SQL SERVER使用发布订阅同步数据库遇到的坑
可能遇到的各种坑 1.在执行 xp_cmdshell 的过程中出错。调用 ‘CreateProcess’ 失败,错误代码: ‘5’ 网上有各种解决办法,包括改本地安全策略,将sql server服务的网络权限改为本机系统,改cmd用户的读写权限,退出360…...
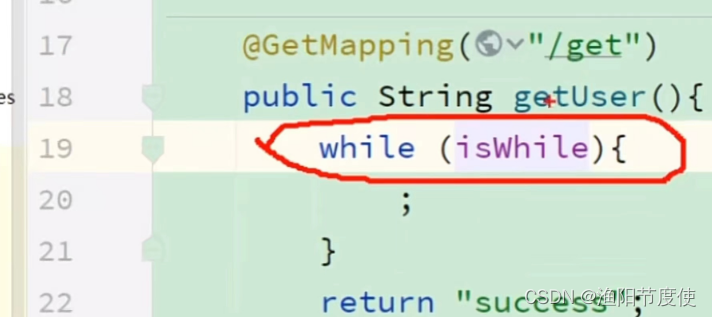
3个命令定位CPU飙高
top 指令找出消耗CPU最厉害的那个进程的pid top -H -p 进程pid 找出耗用CPU资源最多的线程pid printf ‘0x%x\n’ 线程pid 将线程pid转换为16进制 结合jstack 找出哪个代码有问题 jstack 进程pid | grep 16进制的线程pid -A 多少行日志 jstack 进程pid | grep 16进制的线程…...
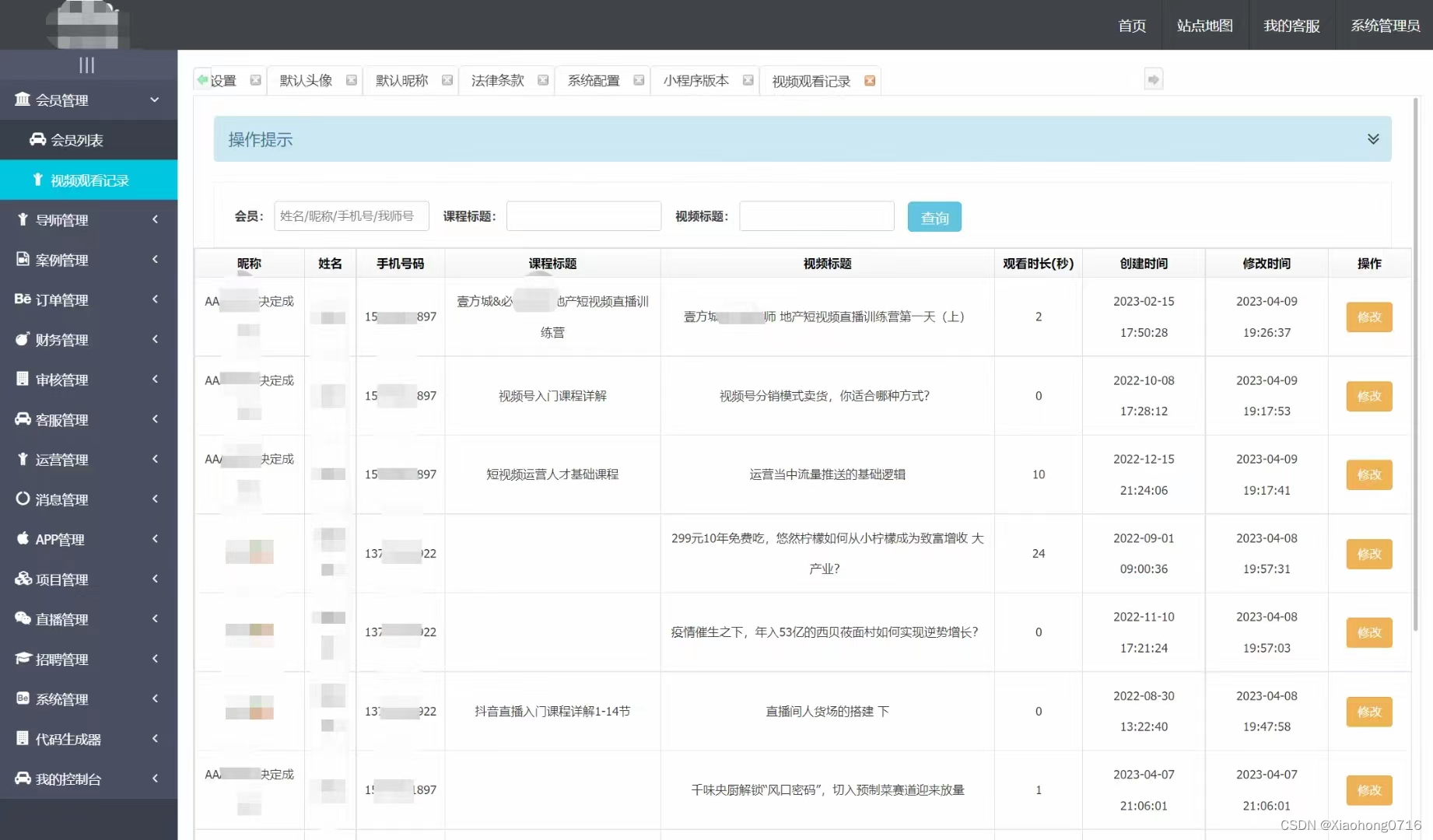
Java版知识付费 Spring Cloud+Spring Boot+Mybatis+uniapp+前后端分离实现知识付费平台免费搭建
提供职业教育、企业培训、知识付费系统搭建服务。系统功能包含:录播课、直播课、题库、营销、公司组织架构、员工入职培训等。 提供私有化部署,免费售后,专业技术指导,支持PC、APP、H5、小程序多终端同步,支持二次开发…...
使用多数据源dynamic-datasource-spring-boot-starter遇到的问题记录
记录使用多数据源dynamic-datasource-spring-boot-starter遇到的问题: 1、工程启动失败 缺少clickhouse连接驱动,引入对应的maven依赖 <!--ck连接驱动--><dependency><groupId>ru.yandex.clickhouse</groupId><artifactId>…...

构建语言模型:BERT 分步实施指南
学习目标 了解 BERT 的架构和组件。了解 BERT 输入所需的预处理步骤以及如何处理不同的输入序列长度。获得使用 TensorFlow 或 PyTorch 等流行机器学习框架实施 BERT 的实践知识。了解如何针对特定下游任务(例如文本分类或命名实体识别)微调 BERT。为什么我们需要 BERT? 正…...
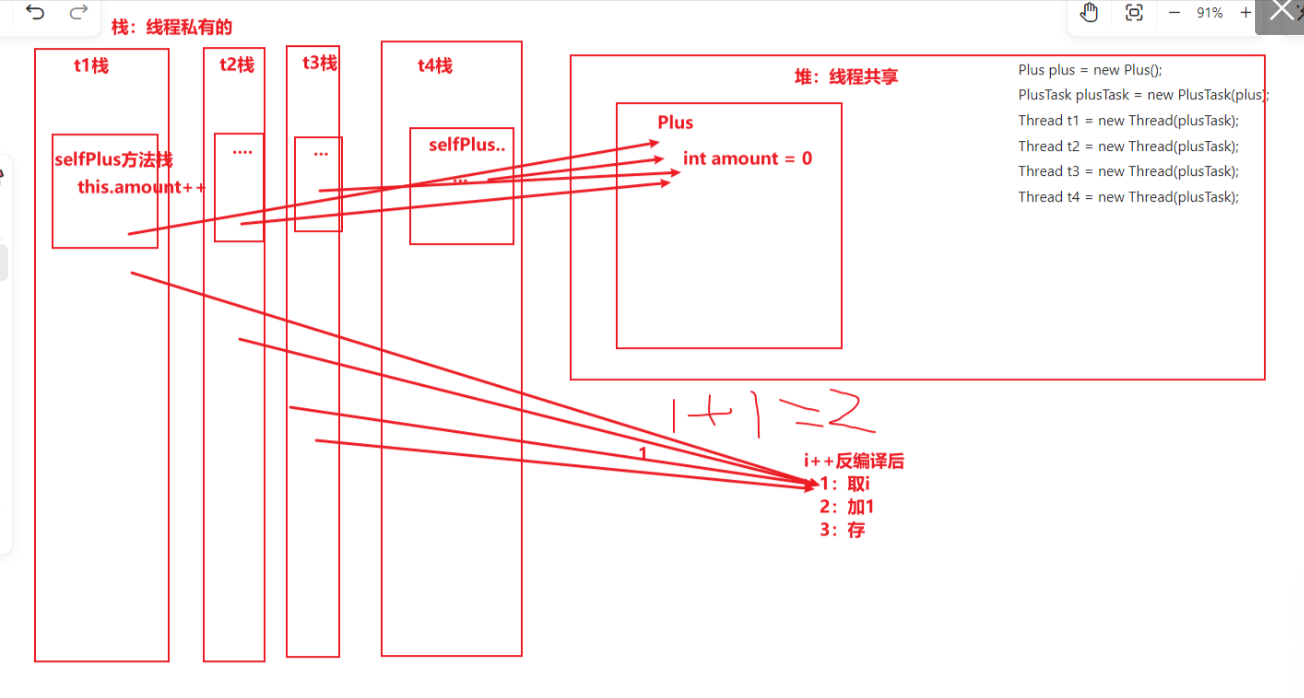
⛳ Java多线程 一,线程基础
线程基础 ⛳ Java多线程 一,线程基础🐾 一,线程基础💭 1.1,什么是程序,进程,线程🏭 1.2,什么是并行和并发👣 1.3,线程使用的场景🎨 1.…...
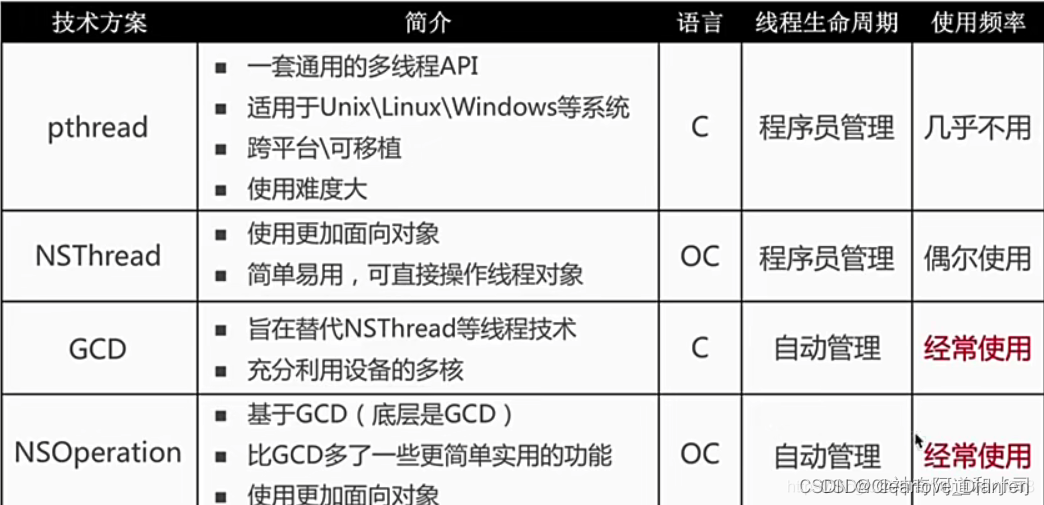
【iOS】多线程 锁问题总结
文章目录 前言1. 你理解的多线程优点缺点 2. atomic 和 nonatomic 的区别及其作用3. GCD的队列类型 - 三种队列类型4. GCD的死锁问题5. 多线程之间的区别和联系6. 进程和线程?进程间的通信方式线程间的通信方式 6. iOS的线程安全手段如何保证 前言 iOS 锁和多线程的…...

Pytorch深度学习-----神经网络之池化层用法详解及其最大池化的使用
系列文章目录 PyTorch深度学习——Anaconda和PyTorch安装 Pytorch深度学习-----数据模块Dataset类 Pytorch深度学习------TensorBoard的使用 Pytorch深度学习------Torchvision中Transforms的使用(ToTensor,Normalize,Resize ,Co…...
Docker啥是数据持久化?
文章目录 数据持久化数据卷相关命令创建读写数据卷创建只读数据卷数据卷共享数据卷容器实现数据卷共享nginx实现数据卷共享nfs总结 Dockerfile持久化Dockerfile方式docker run总结 数据持久化 在容器层的 UnionFS(联合文件系统)中对文件/目录的任何修…...
)
CGAL 线段简化算法(2D)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 线段简化是指:在减少一组折线中顶点数量的同时,尽可能保持整体形状的过程。CGAL中提供了一种迭代算法:通过从一条折线上移除顶点 q q q,迭代地将边 ( p , q...
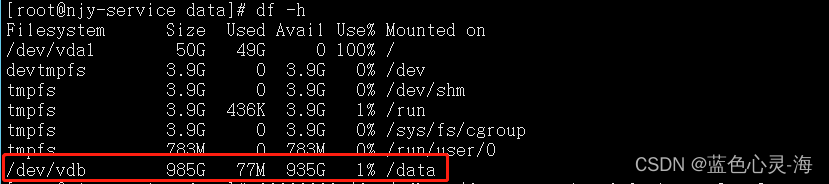
在CentOS 7上挂载硬盘到系统的步骤及操作
目录 1:查询未挂载硬盘2:创建挂载目录3:检查磁盘是否被分区4:格式化硬盘5:挂载目录6:检查挂载状态7:设置开机自动挂载总结: 本文介绍了在CentOS 7上挂载硬盘到系统的详细步骤。通过确…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
