力扣 343. 整数拆分
题目来源:https://leetcode.cn/problems/integer-break/description/
C++题解1:动态规划。dp[i] 代表数字i拆分后得到的最大乘积。递归公式为拆分后两个数的最大乘积相乘,即 dp[i] = max(dp[i], dp[j] * dp[i-j])。对于n=2或3需要另外讨论。
class Solution {
public:int integerBreak(int n) {if(n == 2) return 1;else if(n == 3) return 2;vector<int> dp(n+1, 0);dp[1] = 1;dp[2] = 2;dp[3] = 3;for(int i = 2; i <= n; i++) {for(int j = 1; j < i; j++){dp[i] = max(dp[i], dp[j] * dp[i-j]);}}return dp[n];}
};C++题解2(来源代码随想录):动规五部曲。
- 确定dp数组(dp table)以及下标的含义。dp[i]:分拆数字i,可以得到的最大乘积为dp[i]。
- 确定递推公式。 dp[i]最大乘积是怎么得到的呢?其实可以从1遍历j,然后有两种渠道得到dp[i]。一个是j * (i - j) 直接相乘;另一个是j * dp[i - j],相当于是拆分(i - j),对这个拆分不理解的话,可以回想dp数组的定义。那有同学问了,j怎么就不拆分呢?j是从1开始遍历,拆分j的情况,在遍历j的过程中其实都计算过了。那么从1遍历j,比较(i - j) * j和dp[i - j] * j 取最大的。递推公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));也可以这么理解,j * (i - j) 是单纯的把整数拆分为两个数相乘,而j * dp[i - j]是拆分成两个以及两个以上的个数相乘。
- dp的初始化。初始化dp[2] = 1。
- 确定遍历顺序。先来看看递归公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j))。dp[i] 是依靠 dp[i - j]的状态,所以遍历i一定是从前向后遍历,先有dp[i - j]再有dp[i]。
- 举例推导dp数组
class Solution {
public:int integerBreak(int n) {vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}
};C++题解3(来源代码随想录):贪心算法。“拆分一个数n 使之乘积最大,那么一定是拆分成m个近似相同的子数相乘才是最大的”。每次拆成n个3,如果剩下是4,则保留4,然后相乘,但是这个结论需要数学证明其合理性!
class Solution {
public:int integerBreak(int n) {if (n == 2) return 1;if (n == 3) return 2;if (n == 4) return 4;int result = 1;while (n > 4) {result *= 3;n -= 3;}result *= n;return result;}
};相关文章:

力扣 343. 整数拆分
题目来源:https://leetcode.cn/problems/integer-break/description/ C题解1:动态规划。dp[i] 代表数字i拆分后得到的最大乘积。递归公式为拆分后两个数的最大乘积相乘,即 dp[i] max(dp[i], dp[j] * dp[i-j])。对于n2或3需要另外讨论。 cla…...
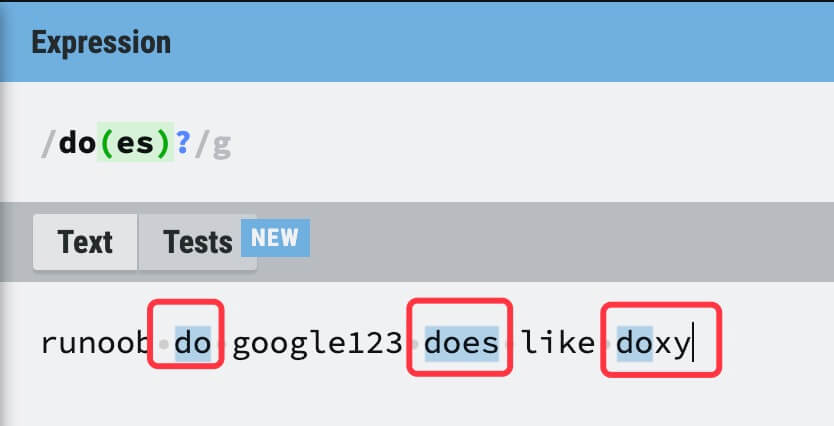
【JavaWeb】正则表达式
🎄欢迎来到边境矢梦的csdn博文,本文主要讲解Java 中正则表达式 的相关知识🎄 🌈我是边境矢梦,一个正在为秋招和算法竞赛做准备的学生🌈 🎆喜欢的朋友可以关注一下🫰🫰&am…...

Vue中常用到的标签和指令
一、标签 在 Vue 中,并没有特定的标签是属于 Vue 的,因为 Vue 是一个用于构建用户界面的框架,可以与 HTML 标签一起使用。Vue 中可以使用的标签和元素基本上与 HTML 标准一致。 以下是一些常见的HTML标签,也可以在 Vue 中使用&a…...

C++设计模式之访问者模式
C访问者设计模式 文章目录 C访问者设计模式什么是设计模式什么是访问者设计模式该模式有什么优缺点优点缺点 如何使用 什么是设计模式 设计模式是一种通用的解决方案,用于解决特定的一类问题。它是一种经过验证的代码组织方式,可以帮助开发人员更快地实…...

Java8的stream常用的操作
记录一下常用的用法 定义测试对象 Datapublic class Employee {//idprivate Integer id;//姓名private String name;//年龄private Integer age;//身高private Double height;//存款private BigDecimal deposit;public Employee(Integer id, String name, Integer age, Double…...

传统计算机视觉
传统计算机视觉 计算机视觉难点图像分割基于主动轮廓的图像分割基于水平集的图像分割交互式图像分割基于模型的运动分割 目标跟踪基于光流的点目标跟踪基于均值漂移的块目标跟踪基于粒子滤波的目标跟踪基于核相关滤波的目标跟踪 目标检测一般目标检测识别之特征一般目标检测识别…...

13-3_Qt 5.9 C++开发指南_基于QReadWriteLock 的线程同步
使用互斥量时存在一个问题: 每次只能有一个线程获得互斥量的权限。如果在一个程序中有多个线程读取某个变量,使用互斥量时也必须排队。而实际上若只是读取一个变量,是可以让多个线程同时访问的,这样互斥量就会降低程序的性能。 例如…...

opencv04-掩膜
opencv04-掩膜 抠图 #include <iostream> #include <opencv2/highgui/highgui.hpp> #include <opencv2/opencv.hpp> #include <vector> #include <array> #include <algorithm>using namespace std; using namespace cv;int main() {str…...

python解析帆软cpt及frm文件(xml)获取源数据表及下游依赖表
#!/user/bin/evn python import os,re,openpyxl 输入:帆软脚本文件路径输出:帆软文件检查结果Excel#获取来源表 def table_scan(sql_str):# remove the /* */ commentsq re.sub(r"/\*[^*]*\*(?:[^*/][^*]*\*)*/", "", sql_str)# r…...

TypeScript
TypeScript 简称: TS ,是 JavaScript 的超集 ,简单来说就是: JS 有的 TS 都有 TypeScript Type JavaScript (在 JS 基础之上, 为 JS 添加了类型支持 ) TypeScript 是 微软 开发…...

解决启动vue前端报错:npm ERR! Missing script: “serve“
目录 一、遇到问题 二、出现报错的两个原因 三、解决办法 一、遇到问题 npm ERR! Missing script: "serve" npm ERR! npm ERR! To see a list of scripts, run: npm ERR! npm run npm ERR! A complet...

数据结构 | 线性数据结构——列表
目录 一、无序列表抽象数据类型 二、实现无序列表:链表 2.1 Node类 2.2 UnorderedList类 三、有序列表抽象数据类型 四、实现有序列表 列表是元素的集合,其中每一个元素都有一个相对于其他元素的位置。更具体地说,这种列表成为无序列表…...
, orr(位或), eor(异或)】)
【ARM 常见汇编指令学习 6 - bic(位清除), orr(位或), eor(异或)】
文章目录 BIC 指令ORR 位或指令EOR 异或指令 上篇文章:ARM 常见汇编指令学习 5 – arm64汇编指令 wzr 和 xzr 下篇文章:ARM 常见汇编指令学习 7 - LDR 指令与LDR伪指令及 mov指令 BIC 指令 指令格式 bic{条件}{S} Rd,Rn,operan…...
)
在CSDN学Golang场景化解决方案(EFK分布式日志系统方案)
一,ElasticSearch 分布式集群部署 在 Golang EFK 分布式日志系统方案中,ElasticSearch 是一个分布式搜索引擎和数据存储库,它可以用于存储和搜索大量的日志数据。以下是 ElasticSearch 分布式集群部署的步骤: 下载 ElasticSearc…...
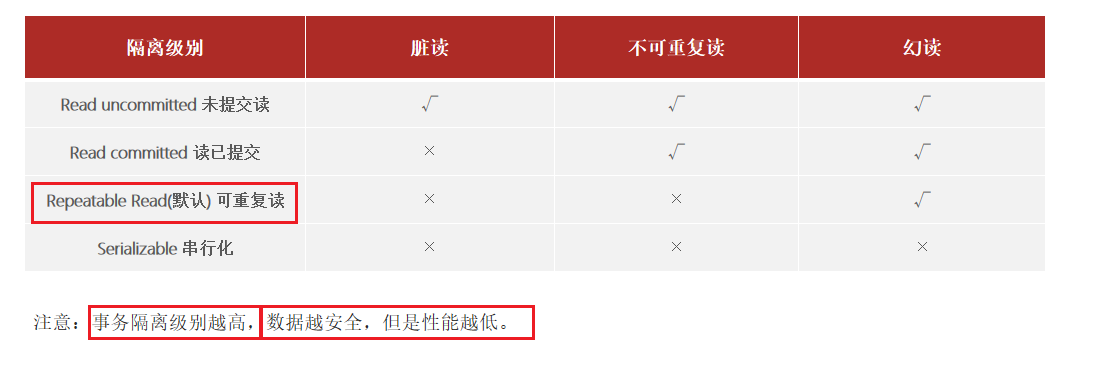
MySQL篇
文章目录 一、MySQL-优化1、在MySQL中,如何定位慢查询?2、SQL语句执行很慢, 如何分析呢?3、了解过索引吗?(什么是索引)4、索引的底层数据结构了解过嘛 ?5、什么是聚簇索引什么是非聚簇索引 ?6、知道什么是回表查询嘛…...

图数据库Neo4j学习四——Spring Data NEO
1配置 1.1Maven依赖 <!--neo4j --> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-neo4j</artifactId> </dependency>1.2yml配置 spring:data:neo4j:uri: bolt://localhost:76…...
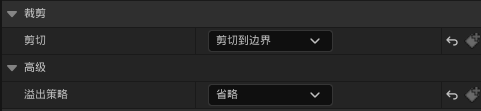
UE虚幻引擎 UTextBlock UMG文本控件超过边界区域以后显示省略号
版本 5.2.1 裁剪 - 剪切 - 剪切到边界 裁剪 - 高级 - 溢出策略 - 省略...

Spring Boot实践五 --异步任务线程池
一、使用Async实现异步调用 在Spring Boot中,我们只需要通过使用Async注解就能简单的将原来的同步函数变为异步函数,Task类实现如下: package com.example.demospringboot;import lombok.extern.slf4j.Slf4j; import org.springframework.s…...
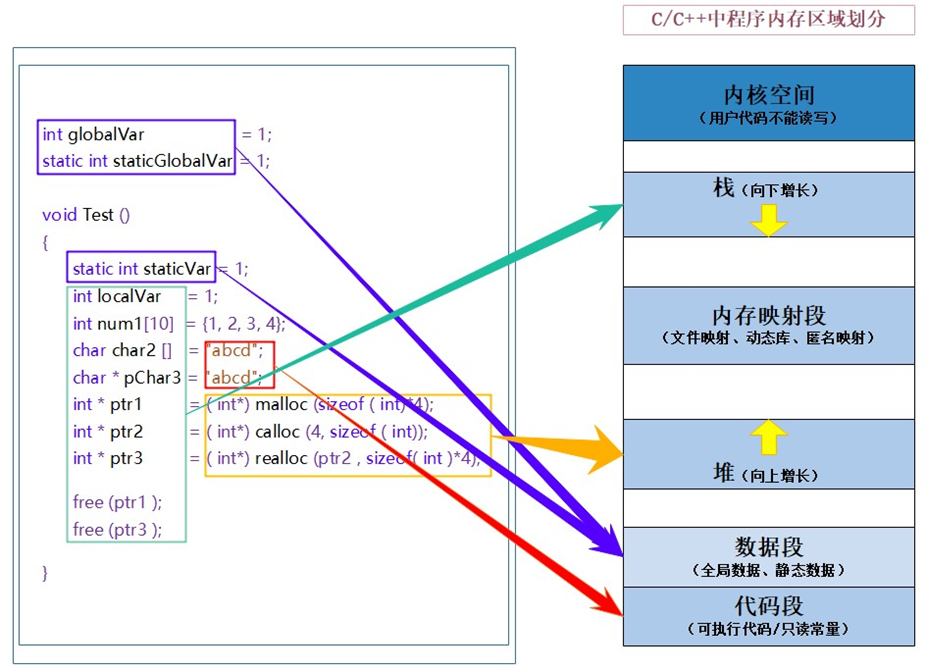
<C语言> 动态内存管理
1.动态内存函数 为什么存在动态内存分配? int main(){int num 10; //向栈空间申请4个字节int arr[10]; //向栈空间申请了40个字节return 0; }上述的开辟空间的方式有两个特点: 空间开辟大小是固定的。数组在声明的时候,必须指定数组的…...

【ASPICE】:学习记录
学习记录 ASPICE中文资料什么是ASPICE过程参考模型 ASPICE全称“Automotive Software Process Improvement and Capability dEtermination”,即“汽车软件过程改进及能力评定”模型框架 ASPICE中文资料 主要资料来源 什么是ASPICE 过程参考模型...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
