哈工大计算机网络课程网络安全基本原理详解之:密钥分发中心与公钥认证中心
哈工大计算机网络课程网络安全基本原理详解之:密钥分发中心与公钥认证中心
在介绍密钥分发中心的概念前,先来回顾一下之前介绍的身份认证协议AP4.0:利用随机数R来避免“回放攻击”,并借助于对称加密算法来保证R的加密传输和解密,从而实现身份认证的协议过程。
共享密钥问题与解决方案
我们知道对称加密算法在发送方/接收方使用的是同一共享密钥,用该密钥加密,同时也需要用该密钥解密。**因此,这里涉及到的一个问题就是,发送方和接收方如何实现密钥的共享,即两个实体在网上如何建立共享密钥。**如果这个问题不能得到很好解决的话,那么共享密钥在网络环境下实施起来就存在很大障碍和安全隐患。
解决方案
比较有代表性的解决方案,就是利用可信任的密钥分发中心(Key Distribution Center-KDC)作为实体间的中介(intermediary)
引入密钥分发中心KDC,就是以它作为中介,实现通信实体之间的共享密钥的分发。
密钥分发中心(KDC)
接下来,我们就看一下作为密钥分发中心,是什么样一个形式,发挥什么样的作用。
我们仍然假设一个通信场景,并以此为基础来介绍KDC在两个实体间通信时的作用机理。
仍然以Alice和Bob两个实体间的通信为例:
-
Alice和Bob间通信需要使用共享对称密钥进行加密,如何获取彼此的密钥呢?
-
引入KDC:一个服务器
- 每个注册用户(很多用户)共享其与KDC的秘密密钥。也就是说,每个用户如果需要使用密钥的话,都需要在KDC上注册一个密钥,该密钥只有用户自己和KDC知道。

- 每个注册用户(很多用户)共享其与KDC的秘密密钥。也就是说,每个用户如果需要使用密钥的话,都需要在KDC上注册一个密钥,该密钥只有用户自己和KDC知道。
-
Alice在KDC上注册一个只有Alice和KDC知道的密钥KA-KDC。
-
Bob在KDC上注册一个只有Bob和KDC知道的密钥KB-KDC。
-
Alice和Bob只知道自己与KDC之间的对称密钥,用于分别与KDC进行秘密通信。
-
Alice在与Bob进行通信时,为了把自己的密钥告知Bob,就需要借助KDC来完成。
Q:KDC如何支持Bob和Alice确定用于彼此通信的共享对称密钥呢?
- Alice利用其与KDC之间共享的密钥KA-KDC,将Alice和Bob的身份信息加密,得到KA-KDC(A,B),然后发送给KDC。
- KDC利用与Alice间的共享密钥对该信息进行解密,并且知道Alice期望与Bob进行通信。为此,KDC为Alice和Bob这次通信生成一个随机数R1。
- KDC将R1和Alice本身的身份标识利用KDC与Bob之间的密钥KB-KDC进行加密,得到KB-KDC(A, R1),之后再将其与R1拼接后,再次利用KA-KDC进行加密,得到KA-KDC(R1,KB-KDC(A, R1))。将该加密的结果发送给Alice。
- Alice收到该加密信息后,利用KA-KDC密钥解密得到随机数R1,该随机数R1就可以作为这次与Bob之间通信所使用的会话密钥。
- 对于KB-KDC(A, R1)这个加密内容,Alice是无法解开的。因为她本次的目的通信对象是Bob,因为在获得这个加密内容后,她会转发给Bob。
- Bob在收到KB-KDC(A, R1)后,可以利用他与KDC共享的密钥KB-KDC解密,从而得到这个随机数R1。
- 此时Bob可以获知Alice的身份认证,并且这次通信的会话使用的秘密的对称密钥就是R1。
- 接下里作为Alice和Bob之间就可以为这次的秘密通信使用R1作为会话密钥(session key),用于共享对称加密。

总结
以上就是KDC在Alice和Bob之间通信过程中,所起的作用和原理。实际上可以看出,KDC的角色相当于是作为一个大家都可以信任的权威机构,每个通信方都需要向其注册申请自己的密钥。在对称加密中,由于需要通信双方共享对称密钥,但实际上,通信双方本身的密钥是不直接利用网络传输给对方的,而是借助于KDC中介,生成一个临时的共享密钥。由这个临时共享密钥来实现通信双发本次会话的对称加密。
公钥认证中心
上面我们介绍了对称密钥在实际应用中,需要借助KDC来实现密钥分发的基本原理和过程。在这一节中,我们针对上述对称密钥方法中存在的问题,来介绍一种公钥会使用的机制:认证中心(CA)。
在之前介绍的身份认证协议AP5.0中,我们介绍了在Alice和Bob间使用对称密钥加密通信时,会存在中间人攻击的问题。事实上,使用公开密钥除了存在这种问题外,还有一个典型的场景就是:比萨恶作剧。
比萨恶作剧
同样以Alice和Bob间的通信为例,看看Trudy(第三方入侵者)可以在通信过程中实施怎样的比萨恶作剧。
-
Ttudy创建邮件订单:Dear Pizza Store: Please deliver to me four pepperon pizzas. Thank you Bob.
上述邮件订单的意思就是,以Bob的名字,向Pizza店订购了4个pizza。
-
为了实现上述恶作剧,Trudy会利用她的私钥签名订单。
-
Trudy向比萨店发送订单。
-
当比萨店索要Bob的公钥时,Trudy向比萨店发送她自己的公钥,但是她声称这是Bob的公钥。
-
由于没有其他机制来验证该公钥是不是真的属于Bob,比萨店只能利用收到的公钥尝试去解密收到的以为是“Bob"发送的签名订单。当然这是能解密的(因为这是一对Trudy的私钥和公钥),因此,基于非对称加密算法,比萨店由于用该公钥解开了之前以为是真实Bob的私钥加密的订单,所以认定该公钥就是属于Bob的。
-
比萨店核实签名,然后向Bob配送了4个比萨。
-
然而可能Bob根本就不喜欢吃比萨,所以这也称为比萨恶作剧。
事实上,我们分析一下,无论是之前的中间人攻击还是比萨恶作剧也好,问题的发生就在于公钥这样一个系统存在一个主要的问题。接下来,我们详细对该问题进行探讨。
公钥问题
核心问题其实上面在讲比萨恶作剧时也提到了,实际上就是,当Alice或者比萨店,当其获得了Bob的公钥时(通过网站,e-mail,磁盘等),她应该如何确定这是真的Bob的公钥,而不是另一个第三方的公钥?
上面的中间人攻击和比萨恶作剧,事实上发生问题的原因,都在于第三方使用了假的公钥来欺骗了接收方。这个问题也就是公钥的主要问题。
如何解决?
同样的,我们可以借助第三方权威认证机构:可信任的认证中心(Certification Authority - CA)。
可信任的认证中心
可信任的认证中心跟我们上面介绍的密钥分发中心KDC类似,它也是一个服务器形式的基础设施,它的主要目的是实现:将网络中通信的实体与其真正的公钥进行绑定。
因此,作为我们在网络通信中要使用公钥的每个人、路由器等,都需要在CA上注册其公钥。
- 每个网络通信实体向CA提供“身份证明”
- CA利用其自己的私钥,对通信实体的公钥进行签名,进而创建绑定通信实体及其公钥的证书(certificate)
- 证书包含了由CA签名的通信实体的公钥—CA声明:这是**的公钥

有了证书之后,将来任何实体需要获取Bob的公钥时,就不会把一个“欺骗性”的密钥当作Bob的密钥,因为它会核实这个密钥的证书是否由权威认证颁发的。
就像大学毕业出去找工作,用人单位不会只听信你自己说:我是***名牌大学毕业的,而是会看你的毕业证书,因为证书是由教育部权威机构颁发的。上面的CA颁发证书也是类似的道理。
有了CA认证中心后,公钥系统就可以比较安全的来运行和实施了。
此时,当Alice想要Bob的公钥时:
- 首先获取Bob的公钥证书(从Bob或其他地方)。
- 应用CA的公钥,解密证书中签名的公钥,从而获得Bob的实际公钥。

公钥证书的主要内容

在示例中包含这样几部分:
- 序列号,认证中心会为每个证书编号,是一个唯一的序列号。
- 证书持有者信息,即对哪个实体的证书进行签名的。包括算法和密钥值。
- 证书发行者信息
- 证书有效期
- 发行者的数字签名
总结:公钥认证中心CA是现在网络公钥系统得以正常运行的重要保障!
相关文章:

哈工大计算机网络课程网络安全基本原理详解之:密钥分发中心与公钥认证中心
哈工大计算机网络课程网络安全基本原理详解之:密钥分发中心与公钥认证中心 在介绍密钥分发中心的概念前,先来回顾一下之前介绍的身份认证协议AP4.0:利用随机数R来避免“回放攻击”,并借助于对称加密算法来保证R的加密传输和解密&…...

md5sum
概念作用及原理 md5sum是一种常用的哈希算法,用于计算数据的MD5哈希值。MD5(Message Digest Algorithm 5)是一种广泛使用的加密散列函数,用于将任意长度的数据映射为固定长度的哈希值(通常是128位)。这个哈…...

图文档数字化:实现高效管理的几大步骤
在当今数字化时代,企业越来越意识到数字化管理对于图文档的重要性。传统的纸质文件管理往往效率低下,容易出现丢失和混乱的情况。为了提高工作效率、降低成本并确保数据安全,许多企业选择采用PDM(产品数据管理)系统来实…...

服务器磁盘占用过高分析
使用命令 du -sh查看出占用较大的目录,如下: 目录大小处理办法/usr/local/mysql/data16G转移部分文件/usr/local/nacos2.1G维持现状/logs4.4G删除部分文件/var1.9G删除部分文件 du -sh命令使用示例: du -sh /* 查看根目录各文件(夹)占用大小…...
【C语言】通讯录3.0 (文件存储版)
前言 通讯录是一种记录联系人信息的工具,包括姓名、电话号码、电子邮件地址、住址等。 文章的一二三章均于上一篇相同,可以直接看第四章改造内容。 此通讯录是基于通讯录2.0(动态增长版)的基础上进行增加文件操作功能,…...

【C#常用操作】
excel相关操作 using Excel Microsoft.Office.Interop.Excel;public Excel.Application app; public Excel.Workbooks wbs; public Excel.Workbook wb; public Excel.Worksheets wss; public Excel.Worksheet ws;/// <summary> /// 取得打开excel句柄 /// </summary…...
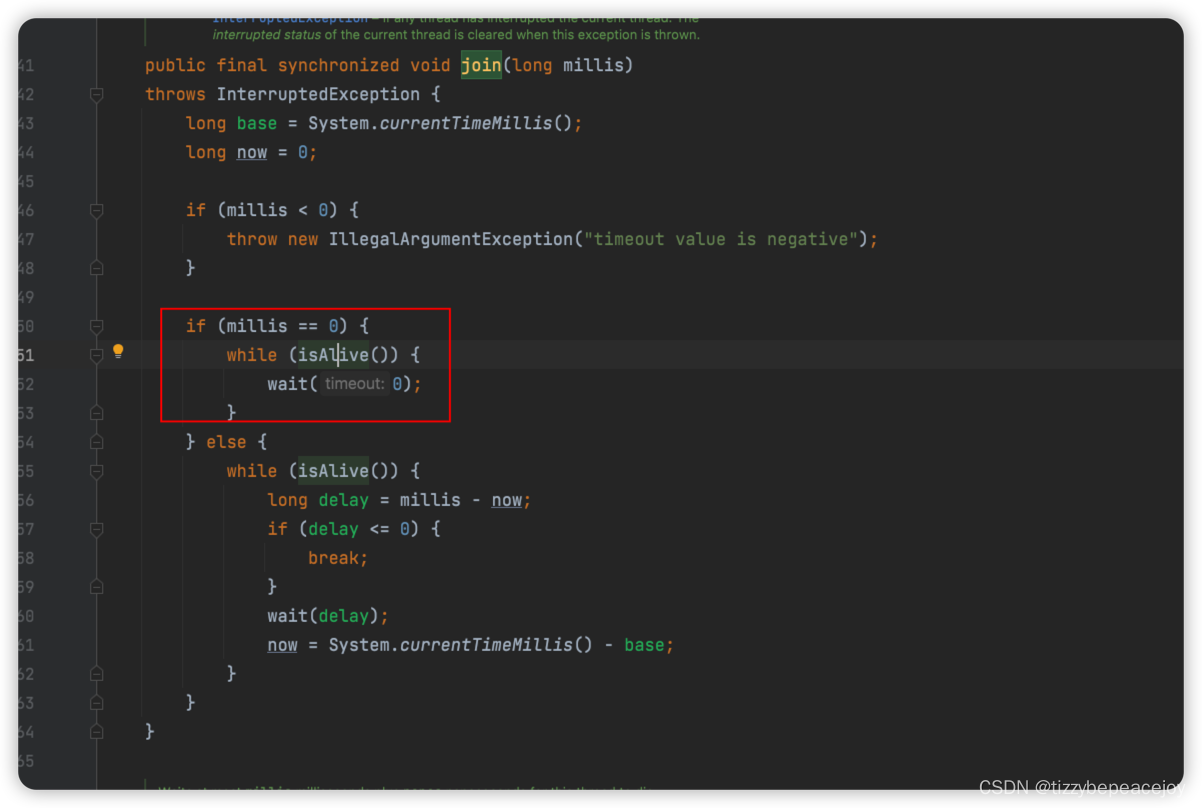
深入理解CountDownLatch计数器
入理解CountDownLatch计数器 其他知识点 Java 多线程基础 深入理解aqs ReentrantLock用法详解 深入理解信号量Semaphore 深入理解并发三大特性 并发编程之深入理解CAS 深入理解CountDownLatch Java 线程池 使用用法 CountDownLatch用法详解 CountDownLatch实现原理 下面例子来…...

从SQL注入绕过最新安全狗WAF中学习fuzz
前言 SQL注入并不是很精通,通过实战绕过WAF来进行加强SQL注入能力,希望对正在学习的师傅能有一丝帮助。 安装 安装前言 我是本地搭建的环境进行测试的 环境是windows11phpstudy2018sqli-labs phpstudy的安装我不再复述,这里简单说一下安全…...

C语言每日一题:12《数据结构》相交链表。
题目: 题目链接 思路一: 1.如果最后一个节点相同说明一定有交点。 2.使用两个循环获取一下长度,同时可以获取到尾节点。 3。注意初始化lenA和lenB为1,判断下一个节点是空是可以保留尾节点的。长度会少一个,尾节点没有…...

【Spring框架】SpringMVC
目录 什么是Spring MVC实现客户端和程序之间的“连接”1.1 RequestMapping1.2GetMapping1.3PostMapping 获取参数2.1.1 获取单个参数2.1.2 获取多个参数2.1.3 获取对象2.2 后端参数重命名2.3 RequestBody 接收JSON对象2.4 获取URL中参数PathVariable2.5 上传⽂件RequestPart2.6…...

HDFS中namenode安全模式
HDFS中namenode安全模式 安全模式的现象探究step1step2step3step4 安全模式的概述控制进入时间和离开条件安全模式自动进入离开安全模式手动进入离开 安全模式的现象探究 step1 HDFS集群在停机状态下,使用hdfs -daemon命令逐个进程启动集群,观察现象首…...
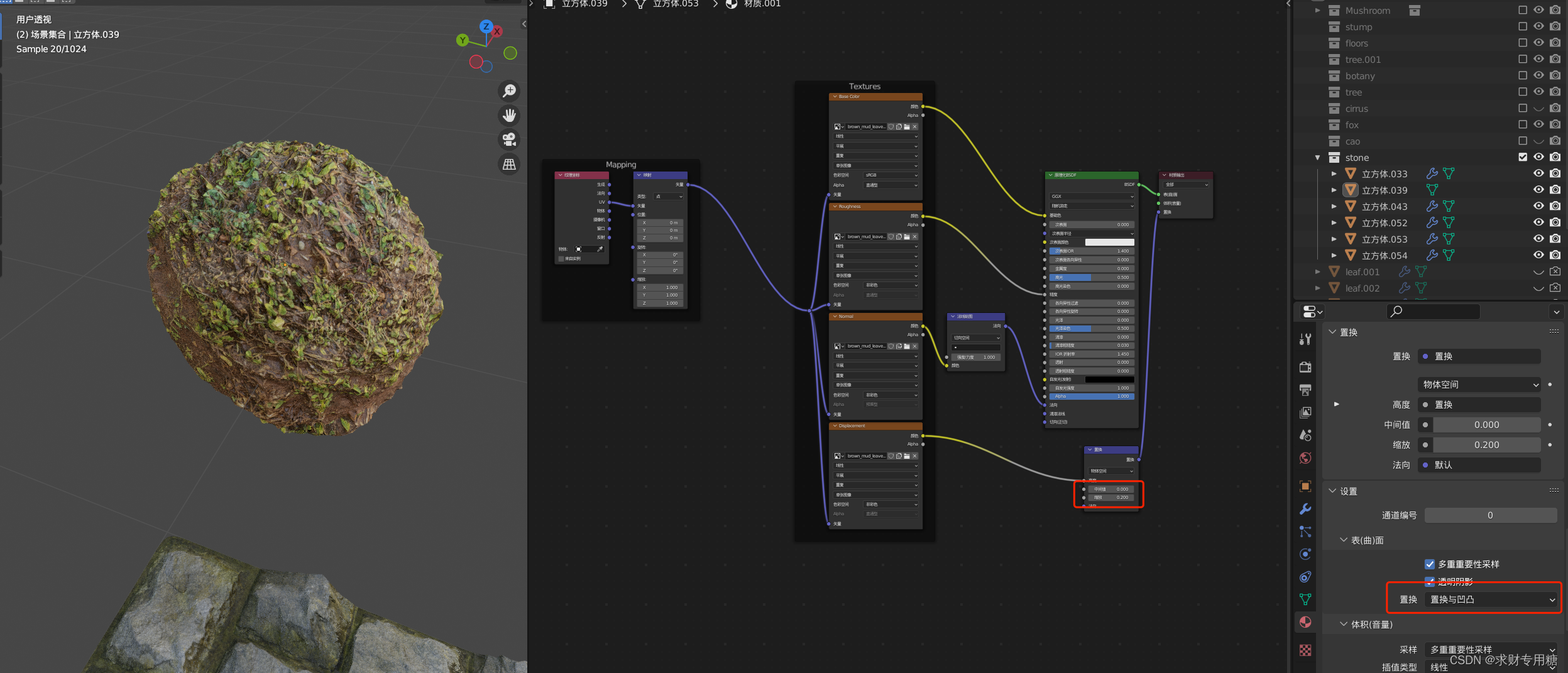
blender凹凸感和置换形变
一、怎么做出凹凸感 需要三个部分的内容: 1、一个基础的纹理:告诉计算机需要用一个什么样的纹理做凹凸,纹理一般采用黑白,在计算机里面,从 0 - 1之间的值可以用从黑到白之间不同的灰度来表示因此,有一张黑白…...
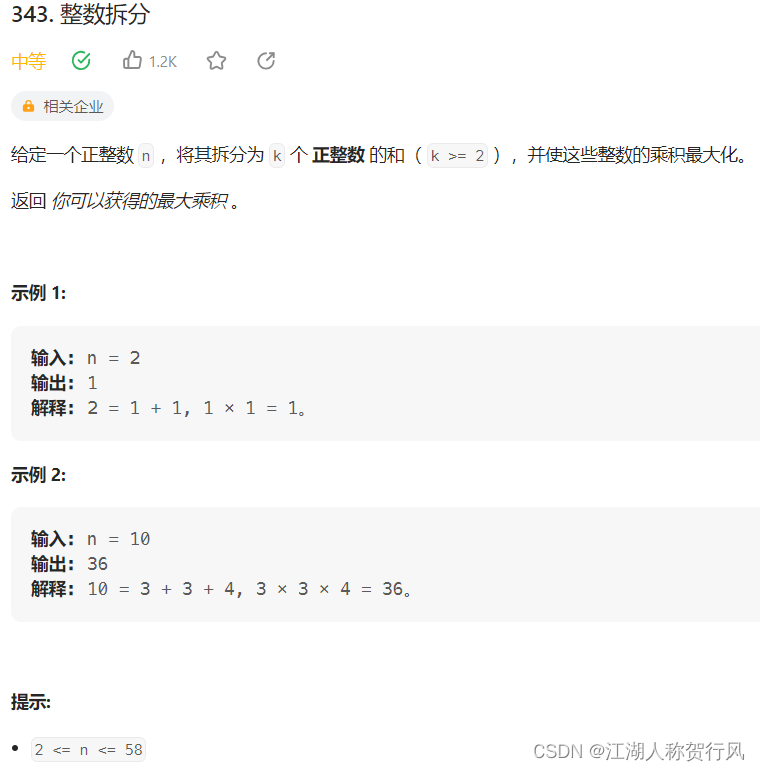
力扣 343. 整数拆分
题目来源:https://leetcode.cn/problems/integer-break/description/ C题解1:动态规划。dp[i] 代表数字i拆分后得到的最大乘积。递归公式为拆分后两个数的最大乘积相乘,即 dp[i] max(dp[i], dp[j] * dp[i-j])。对于n2或3需要另外讨论。 cla…...
【JavaWeb】正则表达式
🎄欢迎来到边境矢梦的csdn博文,本文主要讲解Java 中正则表达式 的相关知识🎄 🌈我是边境矢梦,一个正在为秋招和算法竞赛做准备的学生🌈 🎆喜欢的朋友可以关注一下🫰🫰&am…...

Vue中常用到的标签和指令
一、标签 在 Vue 中,并没有特定的标签是属于 Vue 的,因为 Vue 是一个用于构建用户界面的框架,可以与 HTML 标签一起使用。Vue 中可以使用的标签和元素基本上与 HTML 标准一致。 以下是一些常见的HTML标签,也可以在 Vue 中使用&a…...

C++设计模式之访问者模式
C访问者设计模式 文章目录 C访问者设计模式什么是设计模式什么是访问者设计模式该模式有什么优缺点优点缺点 如何使用 什么是设计模式 设计模式是一种通用的解决方案,用于解决特定的一类问题。它是一种经过验证的代码组织方式,可以帮助开发人员更快地实…...

Java8的stream常用的操作
记录一下常用的用法 定义测试对象 Datapublic class Employee {//idprivate Integer id;//姓名private String name;//年龄private Integer age;//身高private Double height;//存款private BigDecimal deposit;public Employee(Integer id, String name, Integer age, Double…...

传统计算机视觉
传统计算机视觉 计算机视觉难点图像分割基于主动轮廓的图像分割基于水平集的图像分割交互式图像分割基于模型的运动分割 目标跟踪基于光流的点目标跟踪基于均值漂移的块目标跟踪基于粒子滤波的目标跟踪基于核相关滤波的目标跟踪 目标检测一般目标检测识别之特征一般目标检测识别…...

13-3_Qt 5.9 C++开发指南_基于QReadWriteLock 的线程同步
使用互斥量时存在一个问题: 每次只能有一个线程获得互斥量的权限。如果在一个程序中有多个线程读取某个变量,使用互斥量时也必须排队。而实际上若只是读取一个变量,是可以让多个线程同时访问的,这样互斥量就会降低程序的性能。 例如…...

opencv04-掩膜
opencv04-掩膜 抠图 #include <iostream> #include <opencv2/highgui/highgui.hpp> #include <opencv2/opencv.hpp> #include <vector> #include <array> #include <algorithm>using namespace std; using namespace cv;int main() {str…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
