时间复杂度为O(nlogn)的两种排序算法
1.归并排序
归并排序的核心思想:如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
归并排序使用的就是分治思想。分治,顾名思义,就是分而治之,将一个大问题分解成小的子问题来解决。小的子问题解决了,大的问题也就解决了。

public class MergeSort {public static void main(String[] args) {int[] arr = new int[] {7,4,2,8,9,5};mergeSort(arr,0,arr.length-1);System.out.println(Arrays.toString(arr));}/*** 归并排序* 原地排序:否 * 稳定排序:是* 空间复杂度:O(n)* 时间复杂度:最好O(nlogn)——最坏O(nlogn)——平均O(nlogn)* @param arr 要排序数组* @param start 数组起始位* @param last 数组结束位* @return*/public static int[] mergeSort(int[] arr,int start,int last) {//也可以是(start+last)/2,这样写是为了防止数组长度很大造成两个相加大于int范围,导致溢出int mid = (last-start)/2+start;if(start<last) {mergeSort(arr,start,mid);//左数组排序mergeSort(arr,mid+1,last);//右数组排序merge(arr,start,mid,last);//合并两数组}return arr;}//合并数组public static int[] merge(int arr[],int start,int mid,int last) {int i=start;//左边数组下标int j=mid+1;//右边数组下标int[] tempArr = new int[last-start+1];//定义临时数组int k=0;while(i<=mid && j<=last) {if(arr[i]<arr[j]) {tempArr[k++] = arr[i++];}else {tempArr[k++] = arr[j++];}}while(i<=mid) {//将左边剩余元素移入到临时数组中tempArr[k++]=arr[i++];}while(j<=last) {//将右边剩余元素移入到临时数组中tempArr[k++]=arr[j++];}//把临时数组中的数据合并到新数组中for(int z=0;z<tempArr.length;z++) {arr[start+z] = tempArr[z];}return arr;}
}
2.快速排序
假设被排序的无序区间为[A[i],…,A[j]]
一、基准元素选取:选择其中的一个记录的关键字 v 作为基准元素(控制关键字);
二、划分:通过基准元素 v 把无序区间 A[I]…A[j] 划分为左右两部分,使得左边的各记录的关键字都小于 v;右边的各记录的关键字都大于等于 v;(如何划分?)
三、递归求解:重复上面的一、二步骤,分别对左边和右边两部分递归进行快速排序。
四、组合:左、右两部分均有序,那么整个序列都有序。上面的第 三、四步不用多说,主要是第一步怎么选取关键字,从而实现第二步的划分?
划分的过程涉及到三个关键字:“基准元素”、“左游标”、“右游标”
基准元素:它是将数组划分为两个子数组的过程中,用于界定大小的值,以它为判断标准,将小于它的数组元素“划分”到一个“小数值的数组”中,而将大于它的数组元素“划分”到一个“大数值的数组”中,这样,我们就将数组分割为两个子数组,而其中一个子数组的元素恒小于另一个子数组里的元素。
左游标:它一开始指向待分割数组最左侧的数组元素,在排序的过程中,它将向右移动。找大于基准值的数。
右游标:它一开始指向待分割数组最右侧的数组元素,在排序的过程中,它将向左移动。找小于基准值的数。
**注意:**上面描述的基准元素/右游标/左游标都是针对单趟排序过程的, 也就是说,在整体排序过程的多趟排序中,各趟排序取得的基准元素/右游标/左游标一般都是不同的。对于基准元素的选取,原则上是任意的。但是一般我们选取数组中第一个元素为基准元素(假设数组是随机分布的)

/*** 快速排序* 原地排序:是* 稳定排序:否* 空间复杂度:O(1)* 时间复杂度:最好O(nlogn)——最坏O(n^2)——平均O(nlogn)*/
public class QuickSort {public static void main(String[] args) {int[] arr = new int[] {6,1,2,7,9,3,4,5,10,8};reQuickSort(arr,0,arr.length-1);System.out.println(Arrays.toString(arr));}public static void swap(int[] arr,int i,int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}public static void reQuickSort(int[] arr,int left,int right) {if(right<=left) {return;//终止递归}else {int partition = partitionIt(arr,left,right);reQuickSort(arr,left,partition-1);//基准元素左边元素进行排序reQuickSort(arr,partition+1,right);//基准元素右边元素进行排序}}public static int partitionIt(int[] arr,int left,int right) {//为什么 j加一个1,而i没有加1,是因为下面的循环判断是从‐‐j和++i开始的.//而基准元素选的array[left],即第一个元素,所以左游标从第二个元素开始比较int i=left;int j=right+1;int pivot = arr[left];// pivot 为选取的基准元素(头元素)while(true) {while(j>left&&arr[--j]>pivot) {}while(i<right&&arr[++i]<pivot) {}if(i>=j) {break;//左右游标相遇时候停止, 所以跳出外部while循环}else {swap(arr,i,j);//左右游标未相遇时停止, 交换各自所指元素,循环继续}}swap(arr,left,j);//基准元素和游标相遇时所指元素交换,为最后一次交换return j;//一趟排序完成, 返回基准元素位置(注意这里基准元素已经交换位置了)}
}
相关文章:

时间复杂度为O(nlogn)的两种排序算法
1.归并排序 归并排序的核心思想:如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。 归并排序使用的就是分治思想。分治&#x…...

java调用onnx模型,支持yolov5和yolov7
不点star不给解答问题 可直接运行主文件:ObjectDetection_1_25200_n.java 或者 ObjectDetection_n_7.java 都可以直接运行两个可以运行的主文件是为了支持不用网络结构的模型,即使是onnx模型,输出的结果参数也不一样,支持以下两种…...
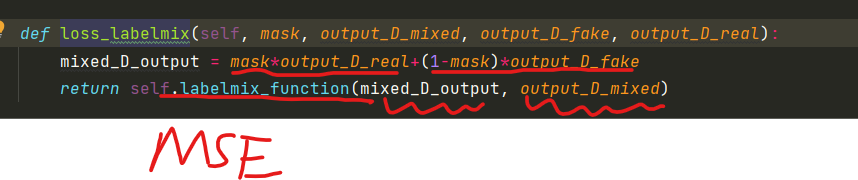
DP-GAN损失
在前面我们看了生成器和判别器的组成。 生成器损失公式: 首先将fake image 和真实的 image输入到判别器中: 接着看第一个损失:参数分别为fake image经过判别器的输出mask,和真实的label进行损失计算。对应于: 其中l…...

自监督去噪:Noise2Void原理和调用(Tensorflow)
文章原文: https://arxiv.org/abs/1811.10980 N2V源代码: https://github.com/juglab/n2v 参考博客: https://zhuanlan.zhihu.com/p/445840211https://zhuanlan.zhihu.com/p/133961768https://zhuanlan.zhihu.com/p/563746026 文章目录 1. 方法原理1.1 Noise2Noise回…...
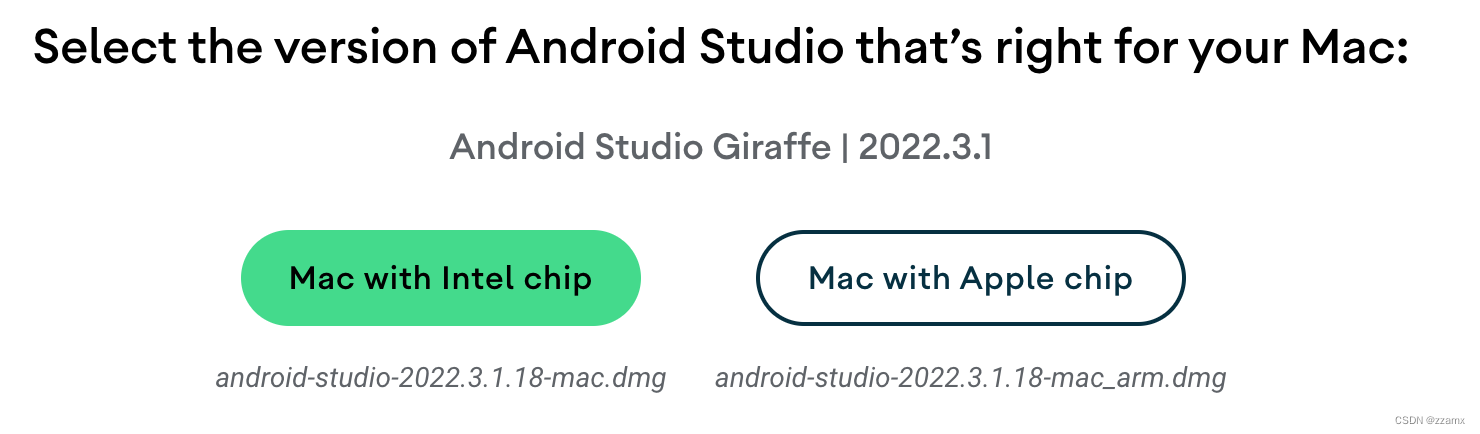
Mac 安装配置adb命令环境(详细步骤)
一、注意:前提要安装java环境。 因为android sdk里边开发的一些包都是依赖java语言的,所以,首先要确保已经配置了java环境。 二、在Mac下配置android adb命令环境,配置方式如下: 1、下载并安装IDE (andr…...
 GDALRasterBand篇 代码示例 翻译 自学)
GDAL C++ API 学习之路 (2) GDALRasterBand篇 代码示例 翻译 自学
GDALRasterBand Class <gdal_priv.h> GDALRasterBand是GDAL中用于表示栅格数据集中一个波段的类。栅格数据集通常由多个波段组成,每个波段包含了特定的数据信息,例如高程、红、绿、蓝色等, 用于表示影像的不同特征。提供了许…...

springboot对静态资源的支持
1、spring boot默认静态路径支持 Spring Boot 默认将 / 所有访问映射到以下目录:** classpath:/static classpath:/public classpath:/resources classpath:/META-INF/resources也就是说什么也不用配置,通过浏览器可以直接访问这几个目录下的文件。 1…...

WPF实战学习笔记27-全局通知
新建消息事件 添加文件:Mytodo.Common.Events.MessageModel.cs using Prism.Events; using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; using System.Windows.Diagnostics;namespace Mytod…...

openSUSE安装虚拟化 qemu kvm
1) 第一种:图形界面yast安装虚拟化 左下角开始菜单搜索yast 点一下就能安装,是不是很简单呢 2)第二种: 命令行安装 网上关于openSUSE安装qemu kvm的教程比较少,可以搜索centos7 安装qemu kvm的教程,然后…...
基于linux下的高并发服务器开发(第四章)- 多进程实现并发服务器(回射服务器)
1. socket // 套接字通信分两部分: - 服务器端:被动接受连接,一般不会主动发起连接 - 客户端:主动向服务器发起连接 2.字节序转换函数 当格式化的数据在两台使用不同字节序的主机之间直接传递时,接收端必然错误…...

【程序分析】符号执行
符号执行入门 参考:https://zhuanlan.zhihu.com/p/26927127 给定一个结果,求解对应的程序输入。 经典符号执行与动态符号执行 参考:https://p1kk.github.io/2021/04/04/others/%E7%AC%A6%E5%8F%B7%E6%89%A7%E8%A1%8C&%E6%B1%A1%E7%82…...

实验笔记之——Windows下的Android环境开发搭建
好久一段时间没有进行Android开发了,最新在用的电脑也没有了Android studio了。为此,本博文记录一下最近重新搭建Android开发的过程。本博文仅为本人学习记录用(**别看) 之前博客也对配置Android做过记录 Android学习笔记之——A…...

#rust taur运行报错#
场景:在window11系统上运行 tauri桌面莹应用,提示错误。 Visual Studio 2022 生成工具 安装的sdk11 , rust运行模式是stable-x86_64-pc-window-gnu, 运行npm run tauir dev 一致失败,失败信息如下 原因:1:在window11系…...

学习购药系统源码:从前端到后端的技术探索
本文将带领读者探索购药系统源码,从前端到后端逐步深入,了解其核心功能和实现方式。我们将使用常见的Web技术,包括HTML、CSS、JavaScript、以及Python的Django框架,展示购药系统的技术奥秘。 前端技术探索 HTML结构搭建 购药系…...

第九次CCF计算机软件认证
第一题:中间数 在一个整数序列 a1,a2,…,an 中,如果存在某个数,大于它的整数数量等于小于它的整数数量,则称其为中间数。 在一个序列中,可能存在多个下标不相同的中间数,这些中间数的值是相同的。 给定一个…...

【计算机网络】传输层协议 -- TCP协议
文章目录 1. TCP协议的引入2. TCP协议的特点3. TCP协议格式3.1 序号与确认序号3.2 发送缓冲区与接收缓冲区3.3 窗口大小3.4 六个标志位 4. 确认应答机制5. 超时重传机制6. 连接管理机制6.1 三次握手6.2 四次挥手 7. 流量控制8. 滑动窗口9. 拥塞控制10. 延迟应答11. 捎带应答12.…...
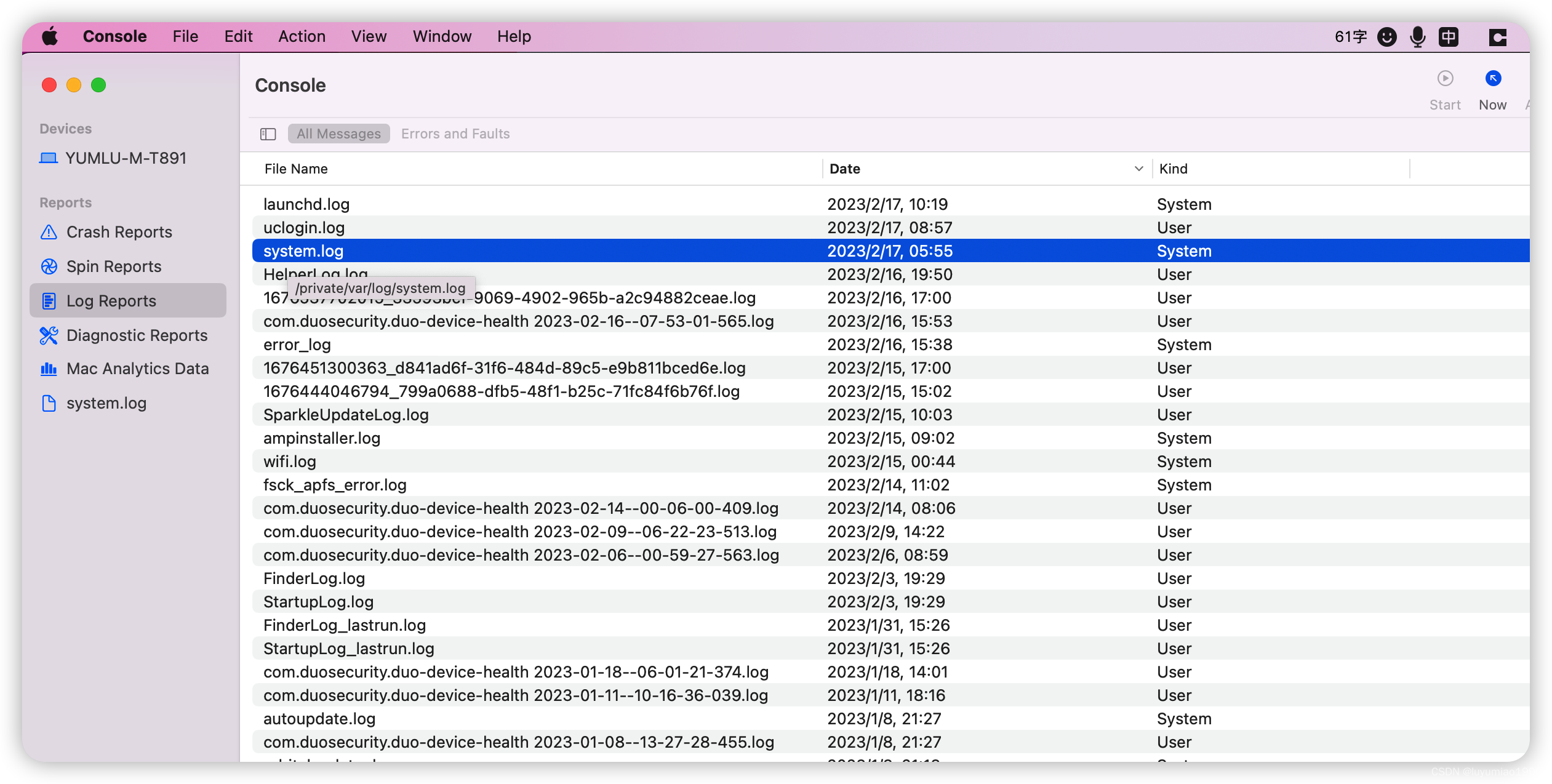
Mac上命令
1. block端口: sudo cp /etc/pf.conf /etc/pf443.conf 编辑pf443.conf,vim /etc/pf443.conf,如 block on en0 proto udp from any to any port 9000 # block UDP port 9000 block on en0 proto tcp from any to any port 5004 # bloc…...

软件安全测试和渗透测试的区别在哪?安全测试报告有什么作用?
软件安全测试和渗透测试在软件开发过程中扮演着不同的角色,同时也有不同的特点和目标。了解这些区别对于软件开发和测试人员来说非常重要。本文将介绍软件安全测试和渗透测试的区别,以及安全测试报告在软件开发和测试过程中的作用。 一、 软件安全测试和…...

Android 从LibVLC-android到自编译ijkplayer播放H265 RTSP
概述 ijkplayer: Android/iOS video player based on FFmpeg n3.4, with MediaCodec, VideoToolbox support. 官方的描述就这么简单的一句话,但丝毫都不影响它的强大。 从LibVLC 到 ijkplayer 截止到2023.7.20 LibVLC-Android 最大的问题在与OOM,测试了…...

如何提升等保水平,减少数据泄露率
如何提升等保水平,减少数据泄露率?随着互联网的发展和数据的普及,数据泄露已经成为了企业面临的重要安全风险之一。为了保障企业的数据安全,国家制定了《网络安全法》和《信息安全等级保护管理办法》,要求企业提升等保…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
