LeetCode343. 整数拆分
343. 整数拆分
文章目录
- [343. 整数拆分](https://leetcode.cn/problems/integer-break/)
- 一、题目
- 二、题解
- 方法一:动态规划
- 方法改良
一、题目
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
提示:
2 <= n <= 58
二、题解
方法一:动态规划
好的,让我们按照动态规划的五个步骤来解决这道题目:
步骤一:确认dp数组以及下标的含义
- dp[i] 表示正整数 i 拆分后可以获得的最大乘积。
步骤二:确认递推公式
- 对于正整数 i,我们可以把它拆分成两个正整数 j 和 i-j,其中 1 <= j < i。
- 那么,对于拆分的两个正整数 j 和 i-j,可以计算它们的乘积 max(j * (i-j))。
- 但我们还需要考虑 j 和 i-j 是否继续拆分,因此递推公式为 dp[i] = max(max(j * (i-j), j * dp[i-j]), max(dp[j] * (i-j), dp[j] * dp[i-j]))。
步骤三:数组初始化
- dp[1] 和 dp[2] 的值分别为 0 和 1,因为它们都不能再拆分。
步骤四:确定遍历顺序
- 我们从小到大遍历正整数 i,从 3 开始遍历到 n,依次计算 dp[i] 的值。
步骤五:举例推导dp数组
让我们通过一个示例来推导 dp 数组。假设输入 n = 6:
进行推导:
- 初始化 dp 数组:
dp = [0, 1]
- 计算 dp[3]:
dp[3] = max(max(1*(3-1), 1*dp[3-1]), max(dp[1]*(3-1), dp[1]*dp[3-1])) = max(max(1*2, 1*1), max(0*2, 0*1)) = 2
- 计算 dp[4]:
dp[4] = 4
- 计算 dp[5]:
dp[5] = 6
- 计算 dp[6]:
dp[6] = 9
最终返回 dp[n],即 dp[6] = 9,表示将正整数 6 拆分后可以获得的最大乘积为 9。
class Solution {
public:int integerBreak(int n) {vector<int> dp(n+1);dp[1] = 0;dp[2] = 1;for(int i = 3; i <= n; i++){int maxm = 1;//i/2是一个改善措施,因为当j>i/2后所有的情况之前都已经产生过了for(int j = 1; j <= i/2; j++){int k = i-j;int temp = max(max(j*k,dp[j]*k),max(dp[k]*j,dp[j]*dp[k]));if(maxm < temp) maxm = temp;}dp[i] = maxm;}return dp[n];}
};
方法改良
在递推公式的计算部分,我们可以将递推公式简化为 dp[i] = max(j * k, j * dp[k]),并且不再计算 dp[j] * dp[k] 部分。
改良的原因:
- 在原始的递推公式中,我们考虑了 j 和 k 是否继续拆分,计算了 dp[j] * dp[k] 部分,但实际上,这部分是在之前的状态中已经计算过的,而且不会再参与当前状态的计算。
- 因此,我们可以直接在递推公式中计算 j * dp[k] 部分,而不再重复计算之前已经得到的 dp[j]。
改良后的代码如下:
cppCopy codeclass Solution {
public:int integerBreak(int n) {vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n; i++) {int maxm = 1;for (int j = 1; j <= i / 2; j++) {int k = i - j;int temp = max(j * k, j * dp[k]);if (maxm < temp) maxm = temp;}dp[i] = maxm;}return dp[n];}
};
相关文章:

LeetCode343. 整数拆分
343. 整数拆分 文章目录 [343. 整数拆分](https://leetcode.cn/problems/integer-break/)一、题目二、题解方法一:动态规划方法改良 一、题目 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整…...

单机,集群和分布式概念
单机的局限性: 1.受限于硬件资源,单机所能承受的用户并发量太少; 2.一个系统有多个模块,任意模块的修改都会导致整个项目代码重新编译、部署; 3.系统中,有些模块是CPU密集型,有些模块是I/O密…...

小目标检测(1)——大恒(DaHeng)相机操作与控制编程
文章目录 引言正文相关开发库的介绍编程准备配置引用头文件GalaxyIncludes.h配置lib文件 具体编程过程初始化和反初始化枚举设备开关设备 属性控制属性控制器种类 图像采集控制和图像处理采单帧回调采集图像处理流对象属性控制 获取设备事件获取掉线事件通知 样例程序分析补充&…...

异步实现邮件发送
目录 问题描述: 问题分析: 问题解决: 分析总结: 问题描述: 在写接口的时候,遇到一个问题,前端要求直接返回结果再去运行其他代码。 问题分析: 因为经费紧张,本次使用…...

【Redis】内存数据库Redis进阶(Redis分片集群)
目录 分布式缓存 Redis 四大问题搭建Redis分片集群分片原理散列插槽(插槽原理)集群伸缩需求设定配置集群伸缩 故障转移自动故障转移手动故障转移 RedisTemplate访问分片集群 分布式缓存 Redis 四大问题 基于 Redis 集群解决单机 Redis 存在的四大问题&a…...

替代LT8711龙讯替代RTD2172 CS5265中文规格书4K60HZ转接线 设计Type-C转HDMI2.0高清投屏方案
龙迅LT8711是一款Type-C/DP1.2 to HDMI2.0方案芯片,北京集睿致远(ASL)推出的CS5265可以完全代替LT8711UX,封装尺寸比LT8711UX小的同时,CS5265的芯片集成度高,内置MCU,内置lLDO等,CS5…...
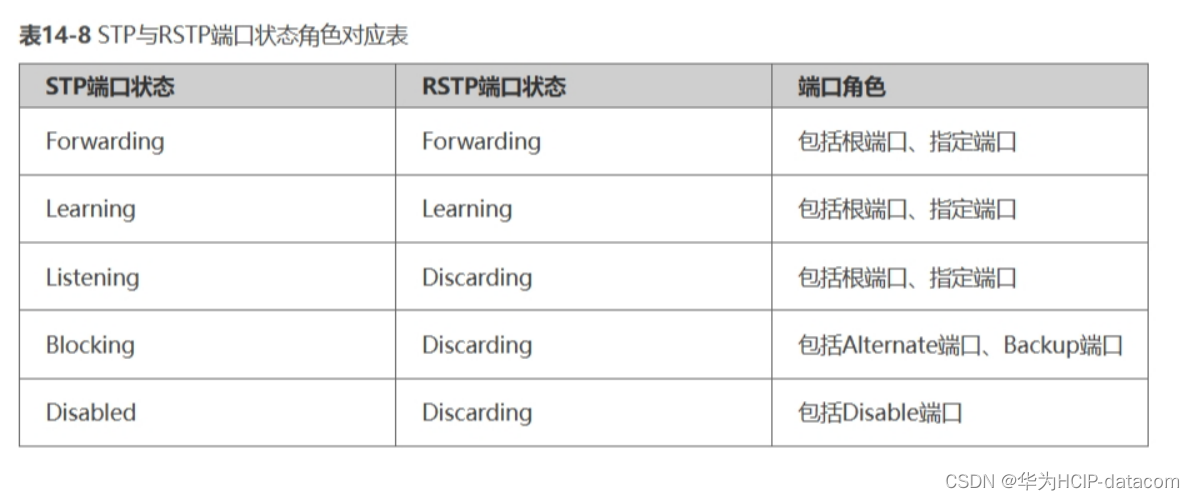
HCIA-datacom数通题库和录播视频资料
HCIA-Datacom,是华为数通认证的初级考试,培训与认证具备数通基础通用知识和技能水平的工程师,只是入门了解数通的一些基础通用知识,适用于小白了解和学习数通知识点起点。 个人建议还是有必要考的,如果在企业考试考试…...

优思学院|质量工程师应具备什么能力?
质量工程师是一个需要耐心、细心、坚持态度、沟通能力、协调能力的工作,更需要持续学习强化自身的专业知识。 质量工程师负责审核、客户投诉的调查、过程的改进以达到质量之提升,他們也必须要预警生产线风险、质量异常,并且协调不同的部門一…...
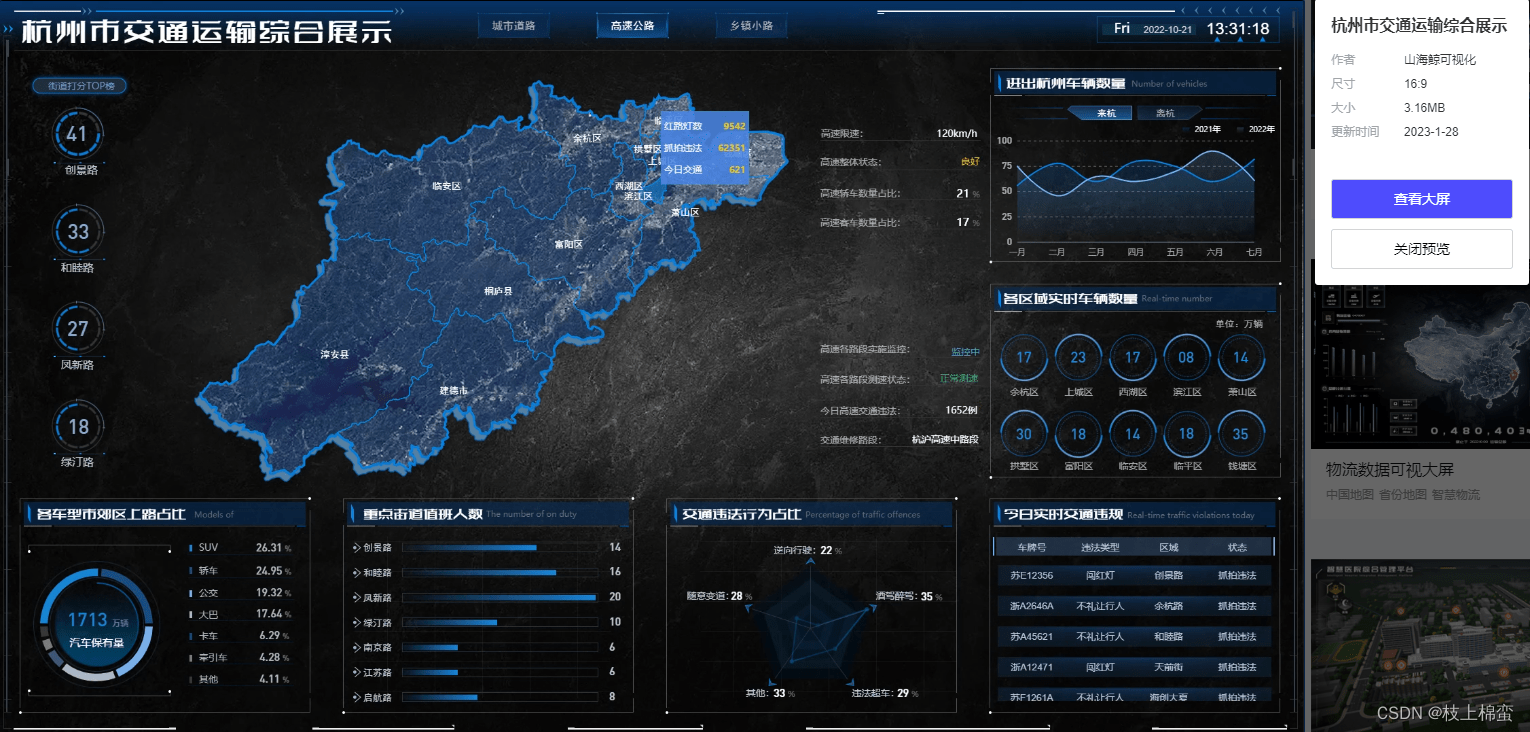
数据分析 VS 数据可视化:决战时刻
数据分析和数据可视化是数据科学领域中两个重要的组成部分,很多人不明白两者之间的关系,会误认为是一个东西,其实不然。本文就带大家简单了解一下它们的区别与联系吧! 数据分析是指通过收集、处理和解释数据来获取有关特定问题或…...

Vue3中无法为el-tree-select设置反选问题分析
环境:Vue3.2、Element Plus 问题:子组件 setting.vue > 弹窗组件 Dialog > 树选择组件el-tree-select ,无法设置默认选中项 default-checked-keys 场景:在一个后台系统的列表页,选中一行数据,点击设置…...

Redis - 缓存持久化
Redis 的缓存持久化有两种技术 : RDB 和 AOF RDB Redis 的数据快照 简单说就是将缓存中的所有数据都记录到磁盘中,当Redis发生故障的时候,只需读取快照文件,就可恢复数据 相应的命令是 save 和 bgsave ,这两个命名…...
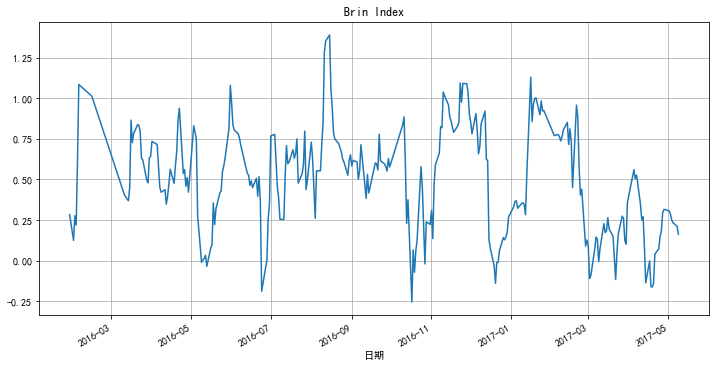
Pandas进阶修炼120题-第三期(金融数据处理,51-80题)
目录 往期内容:第一期:Pandas基础(1-20题)第二期:Pandas数据处理(21-50题) 第三期 金融数据处理51.使用绝对路径读取本地Excel数据方法一:双反斜杠绝对路径方法二:r 拓展…...
3、HAproxy高级配置
基于cookie的会话保持 在 HAProxy 中,可以通过使用 cookie 配置来实现基于 Cookie 的会话保持。cookie 配置用于配置与会话保持相关的选项,允许您定义要在HTTP响应中插入或重写的Cookie以及其他与Cookie会话保持相关的参数。 以下是一些常用的 cookie 配…...

tcpdump网络抓包工具的使用
tcpdump 是一款用在linux系统上的网络抓包工具 1、 基本语法 tcpdump 的常用参数如下: tcpdump -i eth0 -nn -s0 -v port 80-i : 选择要捕获的接口,通常是以太网卡或无线网卡,也可以是 vlan 或其他特殊接口。如果该系统上只有一个网络接口&…...

AMEYA360旗下品牌:日本SUSUMU推出RGV系列贴片电阻器新产品
电动汽车、机器人、精密测量仪器——在上述三例应用领域中,具有高精度、坚固性和长期稳定性的组件是必不可少的。对于这些和类似的应用,RGV系列精密电阻器是理想的选择。 RGV系列电阻器 RGV系列金属薄膜贴片电阻器的电阻值范围为120kΩ至3MΩ(…...
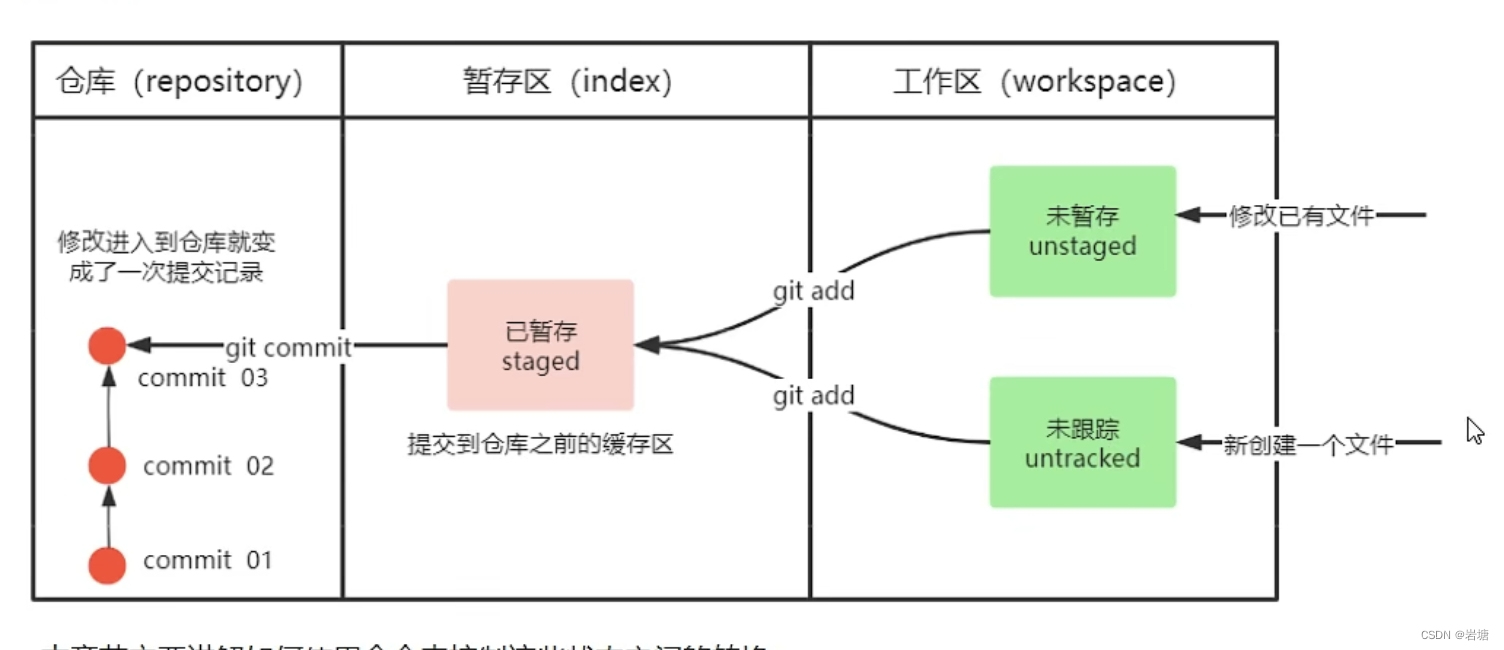
git-版本控制器
集中式版本控制工具(不常用) 版本库集中于中央服务器,team要联网才能工作(下载代码) SVN CVS 分布式版本控制工具 每个电脑上都有一个完整的版本库,工作时无需联网,可以把修改推送给其他人来…...
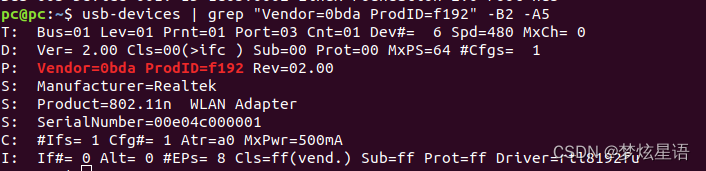
台式机/工控机通过网线共享笔记本电脑无线网络linux系统下 usb网卡的驱动安装
一、台式机/工控机通过网线共享笔记本电脑无线网络 1、 将台式机通过网线和笔记本连接。 2、 将笔记本的“本地连接”和“无线网络连接”的ipv4均设置为自动获取。 4.修改台式机的IP地址为如下(对应笔记本信息) IP地址为192.168.XXX.12 子网掩码为255.2…...

kotlin 编写一个简单的天气预报app(五)增加forcast接口并显示
参考资料 OpenWeatherMap提供了一个/forecast接口,用于获取未来几天的天气预报。你可以使用HTTP GET请求访问该接口,并根据你所在的城市或地理坐标获取相应的天气数据。 以下是一个示例请求的URL和一些常用的参数: URL: http://api.openwe…...
vs调试引发了异常:读取访问权限冲突,argv是0x7
vs2019写了几句小代码,结果报错: 引发了异常:读取访问权限冲突,argv是0x7 查了一堆是什么数组越界了,空指针异常了啥的。 只好都注释掉只留下主函数,结果还是报错,定睛一看才发现原因:main函数忘写第一…...

【电影推荐系统】实时推荐
概览 技术方案: 日志采集服务:通过利用Flume-ng对业务平台中用户对于电影的一次评分行为进行采集,实时发送到Kafka集群。消息缓冲服务:项目采用Kafka作为流式数据的缓存组件,接受来自Flume的数据采集请求。并将数据推…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
