【LeetCode】446. 等差数列划分II -- 子序列
题目链接
文章目录
- 1. 思路讲解
- 1.1 dp表的创建
- 1.2 状态转移方程
- 1.3 使用哈希表找到k
- 1.4 初始化
- 1.5 返回值
- 1.6 该题坑爹的一点
- 2. 代码编写
1. 思路讲解
我们要知道以某个位置为结尾的子序列的数量,可以通过它的以上一位置的为结尾的子序列的数量得知,也就是说,这是一个dp问题。
1.1 dp表的创建
dp问题我们需要创建dp表,如果我们单纯使用dp[i]来表示以 i 位置为结尾的子序列的数量是完全不够的。因为我们不知道以 i-1 位置为结尾的等差数列是怎样的,它的公差是几我们是不知道的。也就是说,我们不确定 i 位置的元素是否能跟到以 i - 1 位置为结尾的数列的后面。
但是,如果知道了数列的后两个元素,也就是知道了 i - 1 位置以及数列中上一个位置的元素,就能知道数列的公差了,也就能知道 i 位置的元素是否能跟到后面了,所以我们需要用两个元素来表示每个dp位置。
创建二维dp表,dp[i][j]表示以 i 位置的元素为数列倒数第二个元素,以 j 位置的元素为数列倒数第一个元素,为结尾的数列数量有多少。(我们人为规定i < j)
1.2 状态转移方程
nums[j] - nums[i]可以得到公差,再由 num[i] - 公差 可以得到上一项的值,记为 a,我们需要知道这个 a 值在nums中是否存在且是否在 i 位置的前面,两个条件都满足才符合题意。
记 a 在nums中的下标为k(至于怎么找到这个k下面会说),我们要找到以 i 和 j 位置为结尾的等差数列的个数,其实找到所有 k 和 i 位置元素结尾的等差数列的个数相加即可(a元素在nums中的位置不只一个,那么k可能就不只一个)。并且也需额外加上一个数列,就是 k,i ,j,本身所构成的等差数列。
那么状态转移方程就为:dp[i][j] += dp[k][i] + 1
1.3 使用哈希表找到k
我们写代码的时候,遍历所有 i 和 j 的组合,时间复杂度就已经到达 N^2 了,如果此时再在数组中去寻找 k ,那么时间复杂度就 N^3了,这大概率是会超时的。
我们可以在dp之前,使用哈希表去将<所有元素,数组下标>绑定在一起,放在哈希表中,这样我们得到了 a 之后,就可以使用哈希表很快地查找到 k 了。
1.4 初始化
刚开始,以 i,j 位置为结尾,只有两个元素,不符合题目中的等差数列,可以记为 0 ,所以我们初始化的时候将dp表中所有的值初始化为 0 即可。又因为,vector会默认初始化为0,所以我们不用手动初始化了。
1.5 返回值
我们要求的是所有的等差数列,所以我们要将所有符合题意的dp[i][j]都加起来然后返回。
1.6 该题坑爹的一点
虽然题目已经说了,返回值以及各个元素的值都在int范围内,但是我们求a的时候,a的值可能会超出int的范围从而出错,所以我们将a的类型要设置为long long。然后用a查找k用的是hash,所以hash的第一个类型也要为long long。
2. 代码编写

class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();// 创建哈希表,便于很快地找到k// 因为k不只一个,所以用vector来存储unordered_map<long long, vector<int>> hash;for (int i = 0; i < n; i++) hash[nums[i]].push_back(i);// 创建二维dp表,第一维为数列的倒数第二个元素,第二维为数列的倒数第一个元素vector<vector<int>> dp(n, vector<int>(n));int ret = 0; // 所有数组的数量// i为nums第0个位置时,不管j为几,dp[0][j]都为0,因为只有两个元素// 所以从第1个位置开始填表即可,且i一定不为nums最后一个元素for (int i = 1; i < n - 1; ++i){// j从i+1开始,一直到最后一个位置,寻找符合题意的情况for (int j = i + 1; j < n; ++j){long long a = (long long)2*nums[i] - nums[j];if (hash.count(a)) // 看a是否存在于hash中{// 如果存在,遍历a对应的vectorfor (auto k : hash[a]){// k需要小于iif (k < i) dp[i][j] += dp[k][i] + 1;}} ret += dp[i][j];}}return ret;}
};
相关文章:

【LeetCode】446. 等差数列划分II -- 子序列
题目链接 文章目录 1. 思路讲解1.1 dp表的创建1.2 状态转移方程1.3 使用哈希表找到k1.4 初始化1.5 返回值1.6 该题坑爹的一点 2. 代码编写 1. 思路讲解 我们要知道以某个位置为结尾的子序列的数量,可以通过它的以上一位置的为结尾的子序列的数量得知,也…...

几个似非而是的注释问题
C 语言的注释可以出现在 C 语言代码的任何地方。这句话对不对?这是我当学生时我 老师问的一个问题。我当时回答是不对。好,那我们就看看下面的例子: A ), int/*...*/i; B ), char* s"…...

【设计模式|上】创建型模式
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 设计模式(上): 简单工厂模式工厂模式抽象工厂模式建造者模式单例模式 1. 正文 1.1 创建型(Creational Patterns) …...

【JS】类 class
【JS】类 class 定义类类的方法类继承静态方法 类(class)是用于创建对象的模板。 我们使用 class 关键字来创建一个类,类体在一对大括号 {} 中,我们可以在大括号 {} 中定义类成员的位置,如方法或构造函数。 每个类中…...
Ubuntu安装harbor(http模式)并随便上传一个
Ubuntu安装harbor(http模式) docker和harbor的介绍就免了,都不知道啥东西,还安装搞毛 先安装docker环境 不要问,软件源之类的配置,挨个梭就行 sudo apt update sudo apt install apt-transport-https ca…...

《向量数据库指南》——腾讯云向量数据库Tencent Cloud Vector DB正式上线公测!提供10亿级向量检索能力
8月1日,腾讯云向量数据库(Tencent Cloud Vector DB)已正式上线公测。在腾讯云官网上搜索“向量数据库”,就可以正式体验该产品。 腾讯云向量数据库不仅能为大模型提供外部知识库,提高大模型回答的准确性,还可广泛应用于推荐系统、文本图像检索、自然语言处理等 AI 领域。…...
1分钟解决github push/pull报错443
1.打开https://www.ipaddress.com/ 2.复制如图IP地址 3.文件夹打开C:\Windows\System32\drivers\etc,复制hosts文件,粘贴到桌面 4.在桌面用记事本打开复制过来的hosts 5.在末尾加上一行,IP写刚才复制的 6.复制桌面的hosts,粘贴回C:\Window…...

vue3学习-ref引用
模板引用 使用特殊的 refattribute 允许再特定的Dom或组件被挂在后,获取他的直接引用。 import { ref } form vue const input ref(null) <input ref"input"/>注意:只可以在组件挂载后才能访问模板引用 #如果你需要侦听一个模板引用 r…...
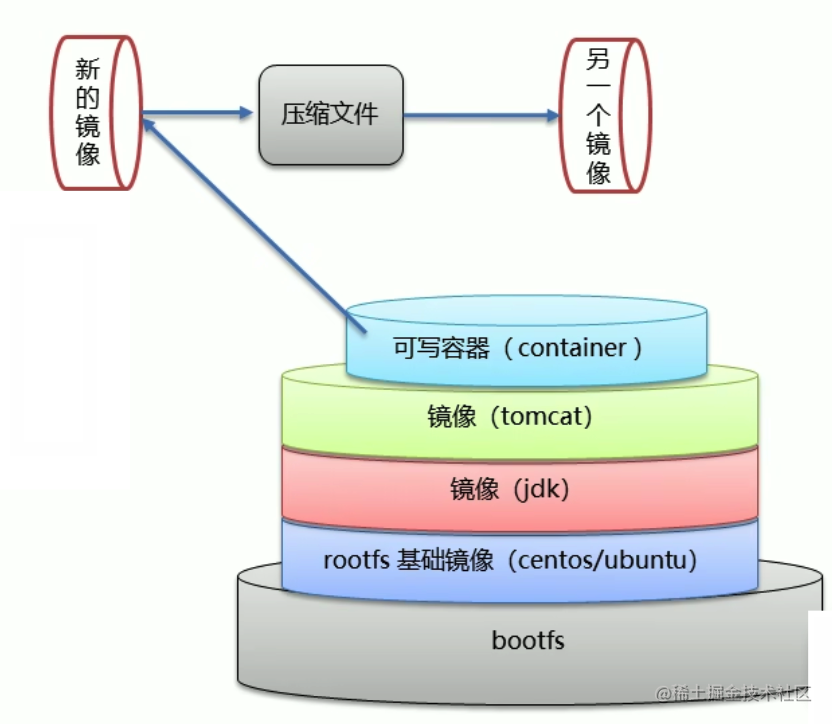
Docker 容器转为镜像
# 容器转成镜像并指定镜像名称与版本号 # commit 时原有容器挂载的目录是不会被写入到新的镜像中去的,数据卷相关的都不会生效 # 但是 root 目录下新建的内容会写入到新的镜像中去 $ docker commit 容器ID 新镜像名称:版本号 $ docker commit -m"描述信息"…...
阿里云服务器免费试用及搭建WordPress网站
文章目录 前言一、免费试用1、选择使用产品2、进行产品配置3、远程连接阿里云服务器①、重置实例密码②、SecureCRT 远程链接③、Workbench 远程链接二、搭建 WordPress 网站1、开放搭建 WordPress 需要的端口2、搭建 LAMP 环境①、Linux 系统升级和更新源②、安装 Apache2③、…...
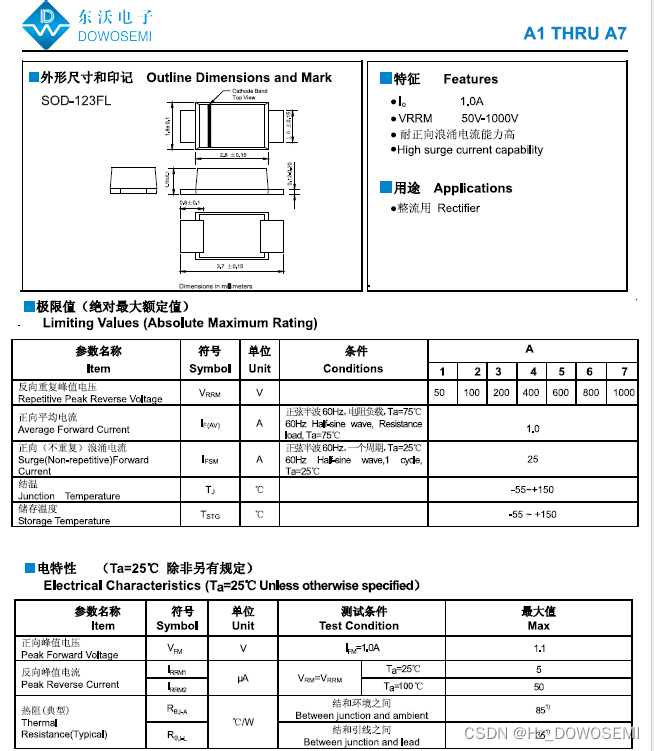
整流二极管型号汇总,超齐全
整流二极管是什么二极管?查看资料可知,整流二极管是一种将交流电能转变为直流电能的半导体器件,可见整流二极管的作用重在“整流”。整流二极管主要用于各种低频半波整流电路,如需达到全波整流需连成整流桥使用。近日,…...

MongoDB 操作命令
创建database 有就切换没有创建 useMydatabase 显示数据库:show dbs显示该database下的 bson对象 show collections 显示该bson下的具体内容**mydatabase.mycollection.find()**查询该bson对象内容**且查询****mydatabase.mycollection.find({a:,b:})****或查询****…...

markdown高级写作技巧汇总
文章目录 1 代码diff2 待办事项3 图片设置宽高4 折叠5 锚点链接实现方式① Markdown 原始写法 [名称](#id)② HTML 语法 名称 6 目录树7 换行 1 代码diff 如果你做过代码 Code Review,对下面这种效果肯定很熟悉 // 数组去重 const unique (arr)>{ - return A…...

SpringBoot自动配置原理入门级理解
简单理解 spring中,我们配置一个bean有两种方式,一种是xml标签的形式,一种是通过java类的形式。那么自动装配就是通过java类的形式来配置bean。 不同的是,springboot将这些我们需要的bean提前配置好了以java类的形式存放在META-I…...

2023 08.02 小记与展望
碎碎念系列更新 算是坚持的第一个月(每个月更新一次,上次是6.29) 主要对上月工作进行总结,并对后续学习内容进行规划。 一、关于工作 7月工作主要涉及以下方面: 1、公司自研APP维护(主要是接口更新和修改…...

MaxPatrol SIEM 增加了一套检测供应链攻击的专业技术
我们为 MaxPatrol SIEM 信息安全事件监控系统增加了一套新的专业技术。 该产品可帮助企业防范与供应链攻击相关的威胁。 此类攻击正成为攻击者的首要目标:它们以软件开发商和供应商为目标,网络犯罪分子通过他们的产品进入最终目标的基础设施。 因此&a…...
!!!)
蓝桥杯上岸每日N题 第六期(求阶乘)!!!
蓝桥杯上岸每日N题第六期 ❗️ ❗️ ❗️ 同步收录 👇 蓝桥杯上岸必背!!!(持续更新中~) 大家好 我是寸铁💪 冲刺蓝桥杯省一模板大全来啦 🔥 蓝桥杯4月8号就要开始了 🙏 距离蓝桥杯省赛倒数…...
Codeforces Round 889 (Div. 2)(视频讲解A——D)
文章目录 A Dalton the TeacherB Longest Divisors IntervalC2 Dual (hard Version)D Earn or Unlock Codeforces Round 889 (Div. 2)(视频讲解A——D) A Dalton the Teacher #include<bits/stdc.h> #define endl \n #define INF 0x3f3f3f3f us…...

K8s安全配置:CIS基准与kube-bench工具
01、概述 K8s集群往往会因为配置不当导致存在入侵风险,如K8S组件的未授权访问、容器逃逸和横向攻击等。为了保护K8s集群的安全,我们必须仔细检查安全配置。 CIS Kubernetes基准提供了集群安全配置的最佳实践,主要聚焦在两个方面:主…...
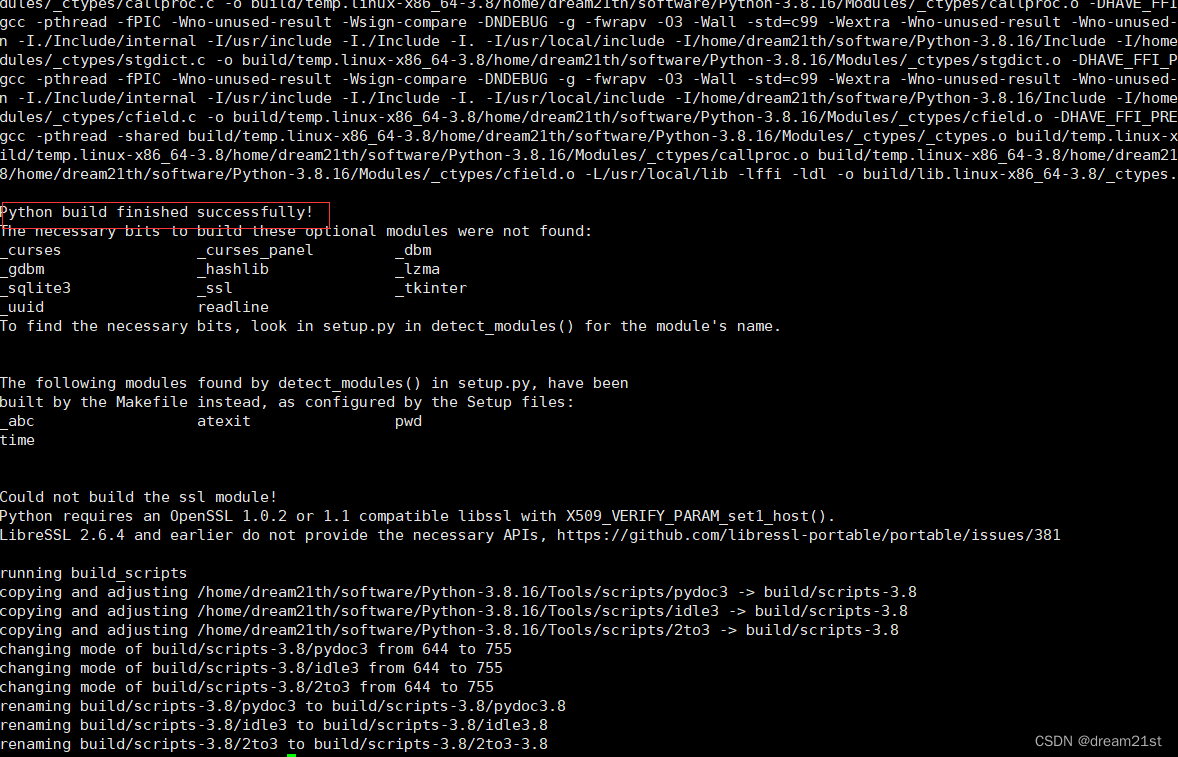
linux安装python和部署Django项目
文章目录 1 python安装2 Django项目部署 1 python安装 官网地址:https://www.python.org/ 本次下载的python安装包地址:https://www.python.org/ftp/python/3.8.16/Python-3.8.16.tgz 解压下载的python压缩包 [rootlocalhost software]# tar -zxvf P…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
