如何停止/重启/启动Redis服务
一、命令行直接启动/停止/重启redis
可以直接通过下面的命令启动/停止/重启redis
/etc/init.d/redis-server start 启动redis服务
/etc/init.d/redis-server stop 停止redis服务
/etc/init.d/redis-server restart 重启redis服务
1、启动redis服务及验证
示例如图:

2、停止redis服务及验证
示例如图:

3、重启redis服务及验证
示例如图:

二、通过redis的相关配置信息关闭/启动redis
还可以通过redis的客户端程序redis-cli的shutdown命令来重启redis

2.启动redis服务及验证
redis-server 默认配置文件启动
redis-server 配置文件路径 指定配置文件启动
例如:
redis-server /etc/redis/redis.conf

相关文章:

如何停止/重启/启动Redis服务
一、命令行直接启动/停止/重启redis 可以直接通过下面的命令启动/停止/重启redis /etc/init.d/redis-server start 启动redis服务 /etc/init.d/redis-server stop 停止redis服务 /etc/init.d/redis-server restart 重启redis服务1、启动redis服务…...
python 的selenium自动操控浏览器教程(2)
人生苦短,我用py 文章目录人生苦短,我用py关于部分网页无法找到元素的问题1方案1方案2关于部分网页无法找到元素的问题2解决方案被网站检查出来我们使用了selenium了怎么办?如何实现前进后退当使用py删除文件时报禁止访问怎么办怎么使用py实现…...

【Deformable Convolution】可变形卷积记录
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 可变形卷积记录 1. 正文 预印版: Deformable Convolutional Networks v1 Deformable ConvNets v2: More Deformable, Better Results 发表版…...

Oracle-Mysql 函数转换
Oracle-Mysql 函数转换limit <> ROWNUMcast <> TO_NUMBERcast as signedcast as unsignedregexp a_\\d <> REGEXP_LIKEschema() <> SELECT USER FROM DUALinformation_schema.COLUMNS表 <> ALL_TAB_COLUMNS表unix_timestampfrom_unixtime <&g…...
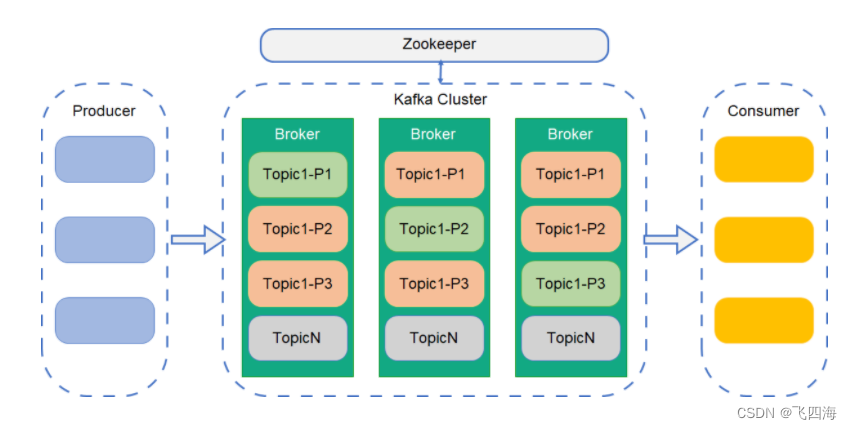
【Kafka】一.认识Kafka
kafka是一个分布式消息队列。由 Scala 开发的高性能跨语言分布式消息队列,单机吞吐量可以到达 10w 级,消息延迟在 ms 级。具有高性能、持久化、多副本备份、横向扩展能力。 生产者往队列里写消息,消费者从队列里取消息进行业务逻辑。 一般在…...

Linux软件管理YUM
目录 yum配置文件 创建仓库 yum查询功能 yum安装与升级功能 yum删除功能 yum仓库产生的问题和解决之道 yum与dnf 网络源 YUM就是通过分析RPM的标头数据后,根据各软件的相关性制作出属性依赖时的解决方案,然后可以自动处理软件的依赖属性问题&…...
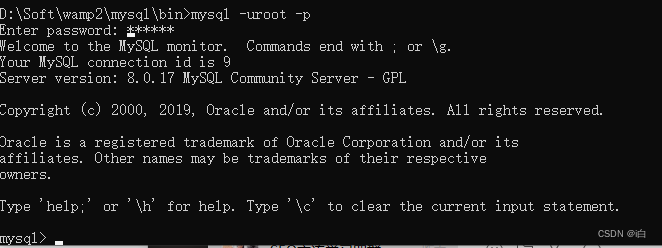
【自学MYSQL】MySQL Windows安装
MySQL Windows安装 MySQL Windows下载 首先,我们打开 MySQL 的官网,网址如下: https://dev.mysql.com/downloads/mysql/在官网的主页,我们首先根据我们的操作系统,选择对应的系统,这里我们选择 Windows&…...

Linux c编程之常用技巧
一、说明 在Linux C的实际编程应用中,有很多有用的实践技巧,编程中掌握这些知识,会对编程有事半功倍的效果。 二、常用技巧 2.1 if 变量条件的写法 main.c: #include <stdio.h>int main(int argc, char *argv[]) {int a =...
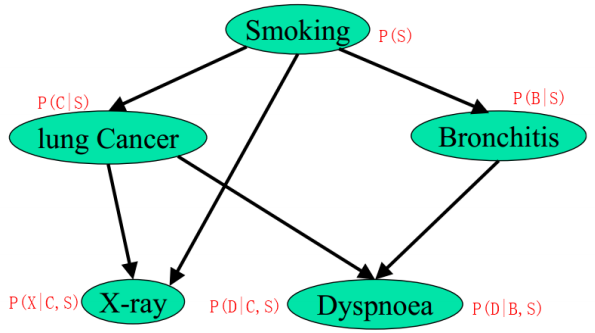
21- 朴素贝叶斯 (NLP自然语言算法) (算法)
朴素贝叶斯要点 概率图模型算法往往应用于NLP自然语言处理领域。根据文本内容判定 分类 。 概率密度公式: 高斯朴素贝叶斯算法: from sklearn.naive_bayes import GaussianNB model GaussianNB() model.fit(X_train,y_train) 伯努利分布朴素贝叶斯算法 fro…...
设计模式第七讲-外观模式、适配器模式、模板方法模式详解
一. 外观模式 1. 背景 在现实生活中,常常存在办事较复杂的例子,如办房产证或注册一家公司,有时要同多个部门联系,这时要是有一个综合部门能解决一切手续问题就好了。 软件设计也是这样,当一个系统的功能越来越强&…...
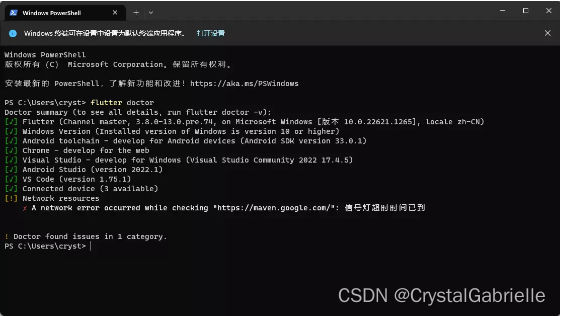
flutter-第1章-配置环境
flutter-第1章-配置环境 本文针对Windows系统。 一、安装Android Studio 从Android Studio官网下载最新版本,一直默认安装就行。 安装完成要下载SDK,可能会需要科学上网。 打开AS,随便创建一个新项目。 点击右上角的SDK Manager 找到SDK…...
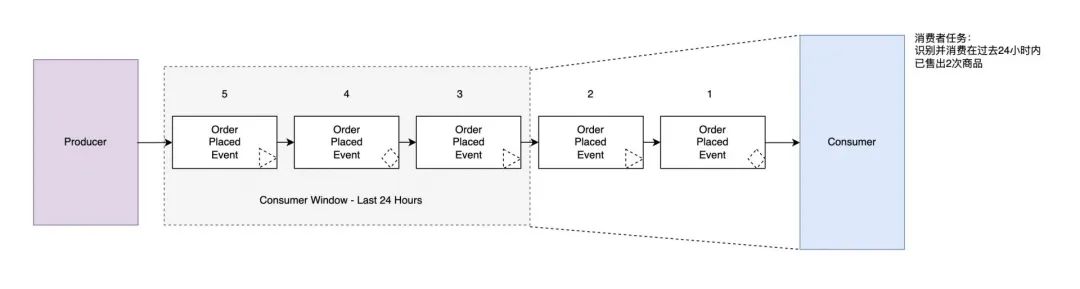
“消息驱动、事件驱动、流 ”的消息模型
文章目录背景消息驱动 Message-Driven事件驱动 Event-Driven流 Streaming事件规范标准简介: 本文旨在帮助大家对近期消息领域的高频词“消息驱动(Message-Driven),事件驱动(Event-Driven)和流(S…...

量化股票配对交易可以用Python语言实现吗?
量化股票配对交易可以用Python语言实现吗?Python 是一种流行的编程语言,可用于所有类型的领域,包括数据科学。有大量软件包可以帮助您实现目标,许多公司使用 Python 来开发与金融界相关的以数据为中心的应用程序和科学计算。 最重…...

机器学习洞察 | 一文带你“讲透” JAX
在上篇文章中,我们详细分享了 JAX 这一新兴的机器学习模型的发展和优势,本文我们将通过 Amazon SageMaker 示例展示如何部署并使用 JAX。JAX 的工作机制JAX 的完整工作机制可以用下面这幅图详细解释:图片来源:“Intro to JAX” video on YouT…...
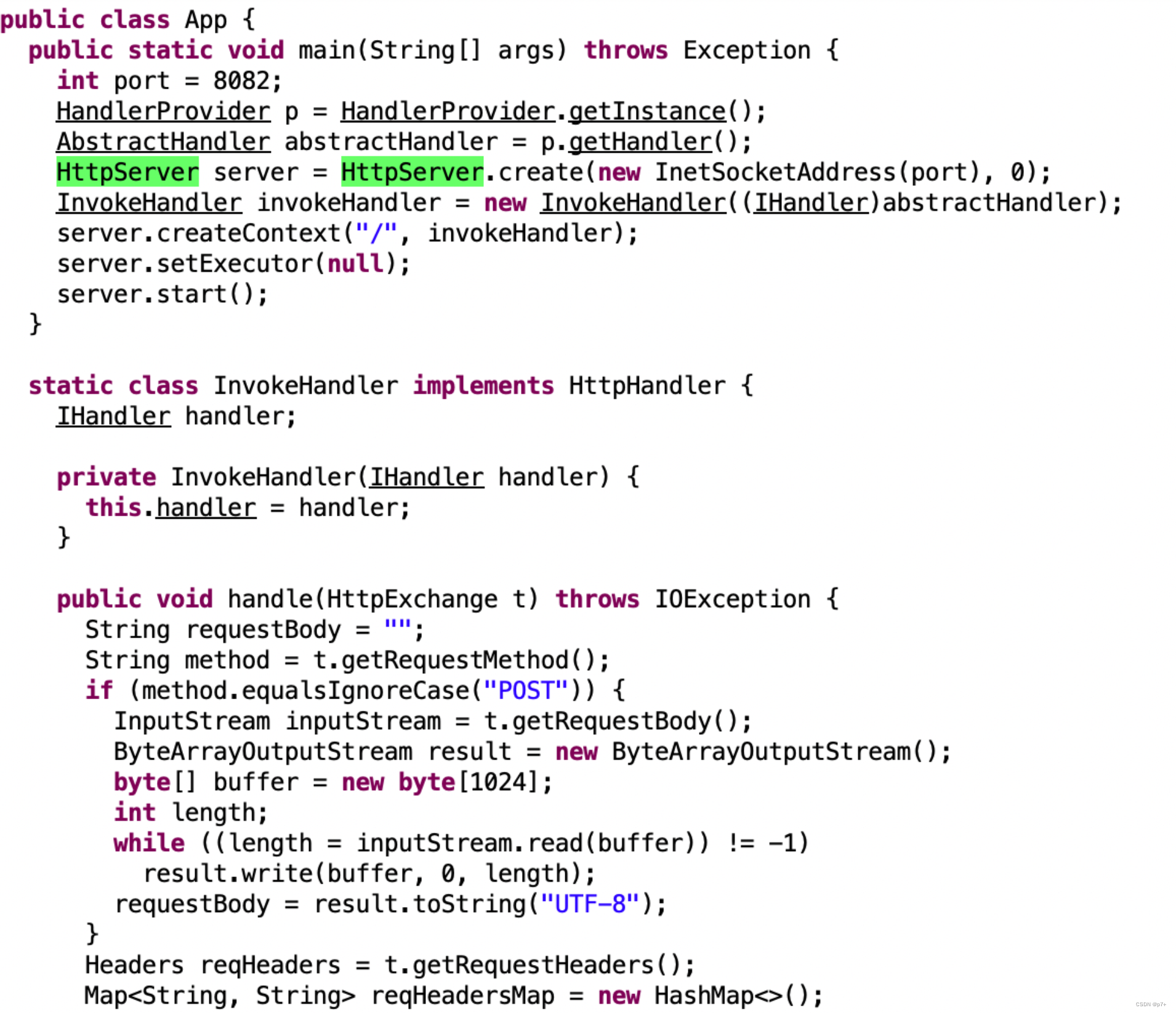
OpenFaaS介绍
FaaS 云计算时代出现了大量XaaS形式的概念,从IaaS(Infrastructure as a Service)、PaaS(Platform as a Service)、SaaS(Software as a Service)到容器云引领的CaaS(Containers as a Service),再到火热的微服务架构,它们都在试着将各种软、硬…...

【算法设计与分析】STL容器、递归算法、分治法、蛮力法、回溯法、分支限界法、贪心法、动态规划;各类算法代码汇总
文章目录前言一、STL容器二、递归算法三、分治法四、蛮力法五、回溯法六、分支限界法七、贪心法八、动态规划前言 本篇共为8类算法(STL容器、递归算法、分治法、蛮力法、回溯法、分支限界法、贪心法、动态规划),则各取每类算法中的几例经典示例进行展示。 一、STL容…...
vue初识
第一次接触vue,前端的html,css,jquery,js学习也有段时间了,就照着B站的视频简单看了一些,了解了一些简单的用法,这边做一个记录。 官网 工具:使用VSCode以及Live Server插件(能够实时预览) 第…...

火山引擎入选《2022 爱分析 · DataOps 厂商全景报告》,旗下 DataLeap 产品能力获认可
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,回复【1】进入官方交流群 2 月 9 日,国内领先的数字化市场研究与咨询机构爱分析发布了《2022 爱分析DataOps 厂商全景报告》(以下简称报告),报…...

java-spring_bean的生命周期
生命周期:从创建到消亡的完整过程初始化容器 1. 创建对象(内存分配 ) 2. 执行构造方法 3. 执行属性注入(set操作) 4. 执行bean初始化方法 使用bean 执行业务操作 关闭/销毁容器 1.执行bean销毁方法 bean销毁时机 容…...
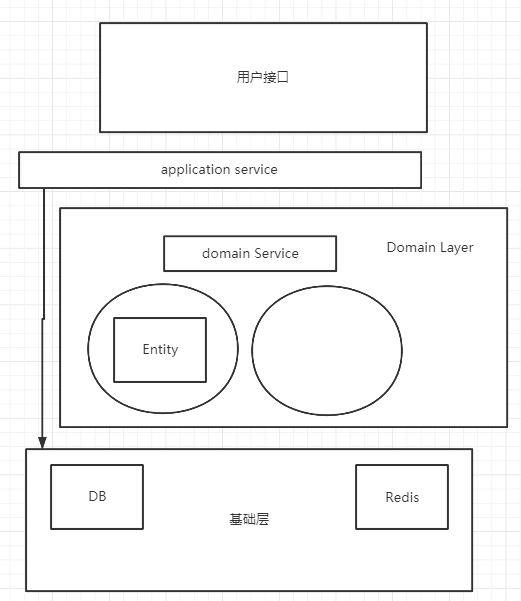
微服务相关概念
一、谈谈你对微服务的理解,微服务有哪些优缺点?微服务是由Martin Fowler大师提出的。微服务是一种架构风格,通过将大型的单体应用划分为比较小的服务单元,从而降低整个系统的复杂度。优点:1、服务部署更灵活࿱…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...
