matplotlib绘制方波圆周分解动画
1 方波的圆周分解
在学习傅里叶变换的时候,有一个经典的示例是方波的分解。我们知道,方波可以分解为无数个正弦波的叠加。而正弦波,又可以看作是圆周运动在一条直线上的投影。当时为了理解这个事情,恐怕大家也花了不少时间。
学习了matplotlib之后,出于学以致用的考虑,我们能不能绘制出动画,来描述上述分解,便于我们来理解呢?
先上动图:

前面学习中已经掌握了matplotlib如何制作动画,以及如何绘制子图。在这个例子中我们将看到以下内容的实战:
- 分割画布为子图
- 绘制圆和波形图
- 调整图像的轴比例
- 隐藏图像的刻度轴
- 设置线型和颜色
- 生成和保存动画
2. 绘图源码
# -*- coding: utf-8 -*-import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np# 把半径放大3倍 画大一些
radius = 4 / np.pi * 3
t = np.deg2rad(list(range(0, 360, 1)))
tc = [tt + 8 for tt in t]# 一级圆
x = np.cos(t) * radius
y = np.sin(t) * radius# 二级圆
x1 = np.cos(3*t) * radius / 3
y1 = np.sin(3*t) * radius / 3# 三级圆
x2 = np.cos(5*t) * radius / 5
y2 = np.sin(5*t) * radius / 5# 四级圆
x3 = np.cos(7*t) * radius / 7
y3 = np.sin(7*t) * radius / 7# 子图的切割
fig, ax = plt.subplots(4, 1)
fig.set_size_inches(5, 8)
fig.tight_layout()
ax[0].set(xlim=(-2, 10), ylim=(-6, 6))#设置横纵坐标等比例且根据轴范围自适应
ax[0].set_aspect("equal", adjustable='datalim')
ax[0].set_axis_off() # 隐藏轴刻度线
# 绘制固定的那个圆
ax[0].plot(x, y, 'b-', linewidth=1)ax[1].set(xlim=(-2, 10), ylim=(-6, 6))
ax[1].set_aspect("equal", adjustable='datalim')
ax[1].set_axis_off()
ax[1].plot(x, y, 'b-', linewidth=1)ax[2].set(xlim=(-2, 10), ylim=(-6, 6))
ax[2].set_aspect("equal", adjustable='datalim')
ax[2].set_axis_off()
ax[2].plot(x, y, 'b-', linewidth=1)ax[3].set(xlim=(-2, 10), ylim=(-6, 6))
ax[3].set_aspect("equal", adjustable='datalim')
ax[3].set_axis_off()
ax[3].plot(x, y, 'b-', linewidth=1)# 动画准备
artists = []
for i in range(0, len(t)):# container用来存储每帧要绘制的内容,通过+=叠加container = []container += ax[0].plot([0, x[i]], [0, y[i]], 'b-', linewidth=1)yy = list(y[i:len(y)])yy.extend(y[0:i])container += ax[0].plot(tc, yy, color='blue', linewidth=1)container += ax[0].plot([x[i], tc[0]], [y[i], yy[0]], 'b--', linewidth=1)container += ax[1].plot([0, x[i]], [0, y[i]], 'b-', linewidth=1)container += ax[1].plot([x1i + x[i] for x1i in x1], [y1i + y[i] for y1i in y1], 'r-', linewidth=1)y_y1 = y+y1yy1 = list(y_y1[i:len(y_y1)])yy1.extend(y_y1[0:i])container += ax[1].plot([x[i], x[i]+x1[i]], [y[i], y[i]+y1[i]], 'r-', linewidth=1)container += ax[1].plot(tc, yy1, color='red', linewidth=1)container += ax[1].plot([x[i]+x1[i], tc[0]], [y[i]+y1[i], yy1[0]], 'r--', linewidth=1)container += ax[2].plot([0, x[i]], [0, y[i]], 'b-', linewidth=1)container += ax[2].plot([x1i + x[i] for x1i in x1], [y1i + y[i] for y1i in y1], 'r-', linewidth=1)container += ax[2].plot([x[i], x[i] + x1[i]], [y[i], y[i] + y1[i]], 'r-', linewidth=1)container += ax[2].plot([x2i + x1[i] + x[i] for x2i in x2], [y2i + y1[i] + y[i] for y2i in y2], 'g-', linewidth=1)container += ax[2].plot([x[i] + x1[i], x[i] + x1[i] + x2[i]], [y[i] + y1[i], y[i] + y1[i] + y2[i]], 'g-',linewidth=1)y_y2 = y + y1 + y2yy2 = list(y_y2[i:len(y_y2)])yy2.extend(y_y2[0:i])container += ax[2].plot(tc, yy2, color='green', linewidth=1)container += ax[2].plot([x[i] + x1[i] + x2[i], tc[0]], [y[i] + y1[i] + y2[i], yy2[0]], 'g--',linewidth=1)container += ax[3].plot([0, x[i]], [0, y[i]], 'b-', linewidth=1)container += ax[3].plot([x1i + x[i] for x1i in x1], [y1i + y[i] for y1i in y1], 'r-', linewidth=1)container += ax[3].plot([x[i], x[i] + x1[i]], [y[i], y[i] + y1[i]], 'r-', linewidth=1)container += ax[3].plot([x2i + x1[i] + x[i] for x2i in x2], [y2i + y1[i] + y[i] for y2i in y2], 'g-', linewidth=1)container += ax[3].plot([x[i] + x1[i], x[i] + x1[i] + x2[i]], [y[i] + y1[i], y[i] + y1[i] + y2[i]], 'g-',linewidth=1)container += ax[3].plot([x3i + x2[i] + x1[i] + x[i] for x3i in x3], [y3i + y2[i] + y1[i] + y[i] for y3i in y3],'c-', linewidth=1)container += ax[3].plot([x[i] + x1[i] + x2[i], x[i] + x1[i] + x2[i] + x3[i]],[y[i] + y1[i] + y2[i], y[i] + y1[i] + y2[i] + y3[i]], 'c-', linewidth=1)y_y3 = y + y1 + y2 + y3yy3 = list(y_y3[i:len(y_y3)])yy3.extend(y_y3[0:i])container += ax[3].plot(tc, yy3, color='cyan', linewidth=1)container += ax[3].plot([x[i] + x1[i] + x2[i] + x3[i], tc[0]], [y[i] + y1[i] + y2[i] + y3[i], yy3[0]],'c--', linewidth=1)artists.append(container)# 生成并保存动图
ani = animation.ArtistAnimation(fig=fig, artists=artists, interval=40)
ani.save(filename="c:/users/admin/desktop/fourier.gif", writer="pillow")
plt.show()这里还有一些优化空间,例如还没有为这幅图加上文字说明(涉及 LaTeX \LaTeX LATEX输入),以及也没有绘制出方波本身。作为一个练习,小白觉得主体的内容已经足够,留待后续优化。

相关文章:

matplotlib绘制方波圆周分解动画
1 方波的圆周分解 在学习傅里叶变换的时候,有一个经典的示例是方波的分解。我们知道,方波可以分解为无数个正弦波的叠加。而正弦波,又可以看作是圆周运动在一条直线上的投影。当时为了理解这个事情,恐怕大家也花了不少时间。 学…...

vue3+ts 实现枚举
首先 index.ts 中定义枚举 export const fruit [{key:1,name:苹果,},{key:11,name:草莓},{key:5,name:香蕉,},{key:51,name:葡萄,},{key:6,name:橙子},{key:7,name:哈密瓜},{key:10,name:西瓜}, ]; 接口返给的数据是一个对象 feeMap{ 1:200, 2&…...

【Python】5分钟了解11个最佳的Python编译器和解释器
11个最佳Python编译器和解释器 1. Brython2. Pyjs3. WinPython4. Skulpt5. Shed Skin6. Active Python7. Transcrypt8. Nutika9. Jython10. CPython11. IronPython结论原文链接 Python是一门初学者的编程语言。它是一种高级语言,非常灵活、解释性和面向对象的语言。…...
如何安装、部署、启动Jenkins
一、测试环境 Linux系统 Centos 7 二、安装步骤: 1、安装jdk 我安装的是jdk8,此处就不多说了,自己百度哈,很简单 2、安装jenkins 首先依次执行如下三个命令: 2.1、导入镜像: [rootcentos7 ~]# sudo …...

sqlalchemy flask长时间未使用 导致数据库连接失效
临时解决方案:在正式运行定时任务之前,先跑一个session.query(),相当于唤醒连接。 参考 https://blog.csdn.net/sinat_42483341/article/details/103723691...

Ubuntu 20.04 系统或图像界面卡死或完全无响应处理方法
Ubuntu 20.04 系统或图像界面卡死或完全无响应处理方法 问题背景无需重启方法安全重启方法 问题背景 Ubuntu 20.04在安装驱动程序时系统突然无响应,终端也无法运行;考虑到尽量不破坏系统,不希望强制上下电重启机器,以免损坏文件系…...
Linux编辑器 - vim使用
1.vim的基本概念 Vim是一个广泛使用的文本编辑器,它是在Unix和Linux系统中常用的命令行文本编辑器之一。 vim的主要三种模式 ( 其实有好多模式,目前掌握这 3 种即可 ), 分别是 命令模式 ( command mode )、 插入模式 ࿰…...

【Windows】磁盘快捷修复
【Windows】磁盘快捷修复 1、背景2、关于Chkdsk3、示例 1、背景 前段时间使用U盘拷贝文件过程中,突然发现U盘无法读取了,U盘里面存储的数据也无法获取。 然后使用windows系统的chkdsk命令进行修复。 chkdsk全称:checkdisk,即磁盘…...
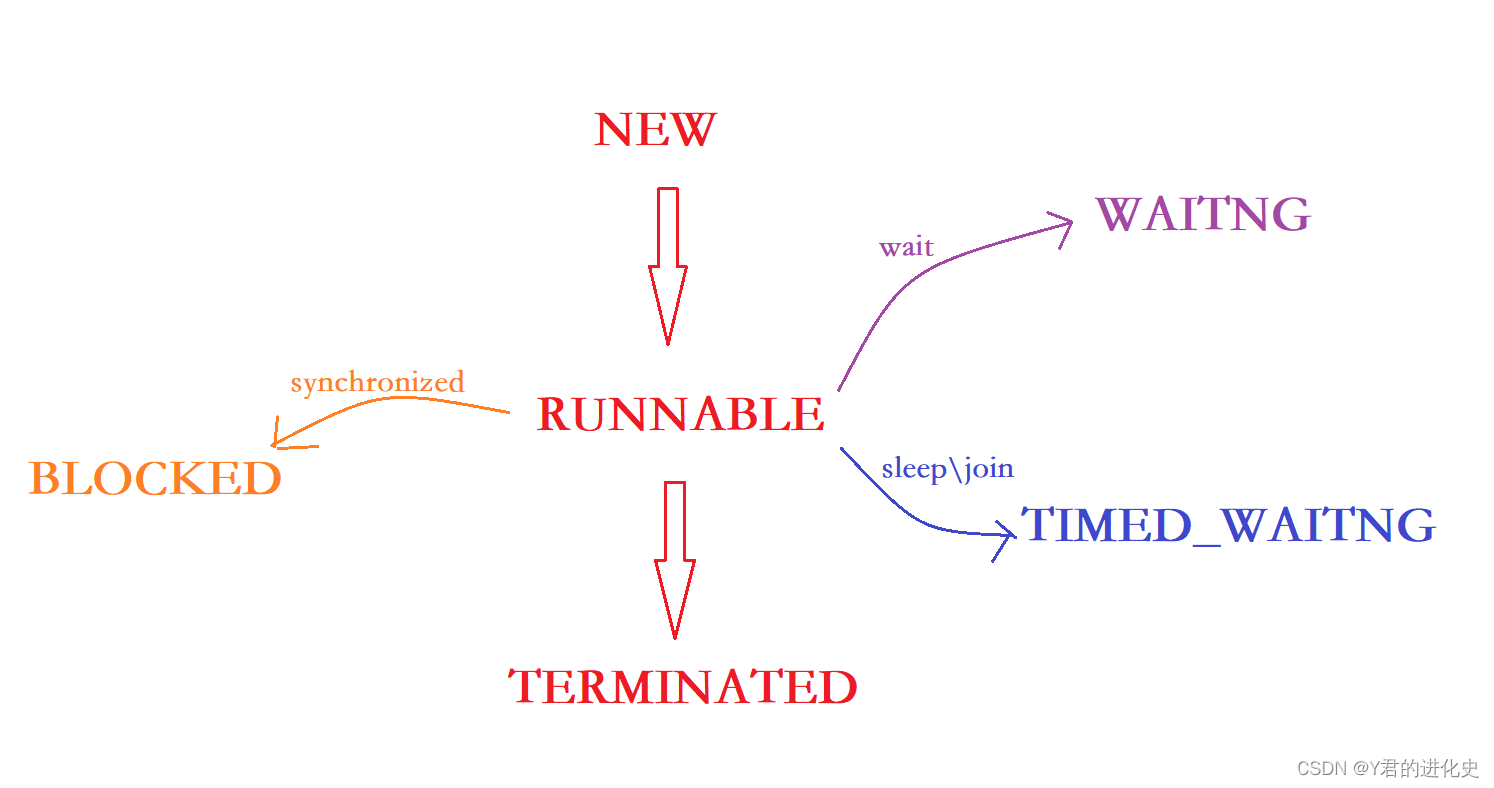
Java 线程的多种状态
前言 在前文中详细介绍了线程的启动、中断、休眠、等待。本文详细介绍线程的多种状态。 获取线程的当前状态代码是: 线程对象.getState(); 目录 前言 一、NEW 二、RUNNABLE 三、BLOCKED 四、WAITNG 五、TIMED_WAITNG 六、TERMINATED 结语 一、NEW Thread 对…...

AI绘画| 迪士尼风格|可爱头像【附Midjourney提示词】
Midjourney案例分享 图片预览 迪士尼风格|可爱头像 高清原图及关键词Prompt已经放在文末网盘,需要的自取 在数字艺术的新时代,人工智能绘画已经迅速崭露头角。作为最先进的技术之一,AI绘画结合了艺术和科学,开启了一…...

【浪费了我两个小时时间】Microsoft store无法加载页面0x80131500
绕的圈,踩的坑 谷歌搜索, newbing搜索都叫我清理缓存,重新安装等方法。 还被这篇文章误导了一下:微软应用商店错误代码0x80072EFD怎么办?(已解决) 加上重启电脑各种试不行。 最后想到要去改代…...

【动态规划】子序列系列
文章目录 动态规划(子序列系列)1. 最长递增子序列2. 摆动序列3. 最长递增子序列的个数4. 最长数对链5. 最长定差子序列6. 最长的斐波那契子序列的长度7. 最长等差数列8. 等差数列划分 || - 子序列 动态规划(子序列系列) 1. 最长递…...

URL存储解锁数据管理的新思路,重新定义数据传输与共享(@vue/repl)
Thinking系列,旨在利用10分钟的时间传达一种可落地的编程思想。 近日,在了解 vue/repl 相关内容,其通过 URL 进行数据存储,感觉思路惊奇,打开了新方式。 首先,通过 URL 存储最大的便利是:无需服…...

matlab程序中文乱码
不同版本的matlab共存在GBK(即,ANSI)和UTF-8两种编码方式,因此可能会出现乱码问题。 第一步:在matlab的命令行窗口输入指令,查看当前编码方式 feature(locale) 第二步:用Notepad打开文件&…...
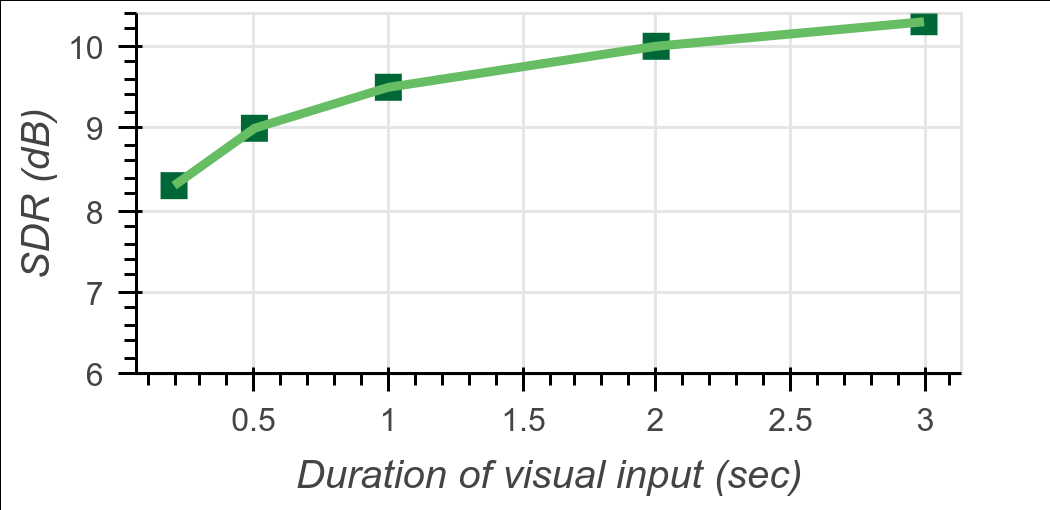
【计算机视觉|语音分离】期望在嘈杂环境中聆听:一个用于语音分离的不依赖于讲话者的“音频-视觉模型”
本系列博文为深度学习/计算机视觉论文笔记,转载请注明出处 标题:Looking to Listen at the Cocktail Party: A Speaker-Independent Audio-Visual Model for Speech Separation 链接:Looking to listen at the cocktail party: a speaker-in…...

curl 介绍和使用
文章目录 一、介绍1.1 curl 介绍1.2 curl 参数介绍1.3 类似Curl的工具和库 二、使用2.1 curl 下载2.2 curl 示例用法2.3 curl命令使用digest方式验证用户 一、介绍 1.1 curl 介绍 官网:https://curl.se/GitHub源码:https://github.com/curl/curl Curl…...

5、VMWARE安装、MobaXterm SSH连接 、Ubuntu xrdp安装使用
以下是在VMware中安装Ubuntu 22.04的详细步骤: 下载Ubuntu 22.04镜像文件: 前往Ubuntu官方网站或其他可信来源,下载Ubuntu 22.04的镜像文件(.iso格式)。 创建虚拟机: 打开VMware Workstation软件…...

Docker dockerfile 案例:centos 支持 vim
创建一个 centos 容器,容器内默认是不支持使用 vim 指令的,只能使用 vi 指令。(附:Dockerfile 语法与指令) 但想在创建 centos 容器后就支持 vim 指令,需要自定义 centos,编写 dockerfile&…...

Git忽略已经提交过一次的文件 Git忽略文件
1、从未提交过的文件可以用.gitignore 也就是添加之后从来没有提交(commit)过的文件,可以使用.gitignore忽略该文件 该文件只能作用于未跟踪的文件(Untracked Files),也就是那些从来没有被 git 记录过…...

Scala项目找不到或无法加载主类
目录 1,出错背景2,分析与解决 1,出错背景 Scala项目无法创建scale和Java文件。项目没有报错,但执行时项目总是找不到项目下的类,报错信息如下所示: 错误: 找不到或无法加载主类 com.my.memTestCheck但该类…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...

python读取SQLite表个并生成pdf文件
代码用于创建含50列的SQLite数据库并插入500行随机浮点数据,随后读取数据,通过ReportLab生成横向PDF表格,包含格式化(两位小数)及表头、网格线等美观样式。 # 导入所需库 import sqlite3 # 用于操作…...
