两行CSS让页面提升渲染性能
content-visibility是CSS新增的属性,主要用来提高页面渲染性能,它可以控制一个元素是否渲染其内容,并且允许浏览器跳过这些元素的布局与渲染。
content-visibility: hidden的效果与display: none类似其区别在于:
- content-visibility: hidden 只是隐藏了子元素,自身不会被隐藏
- content-visibility: hidden 隐藏内容的渲染状态会被缓存,所以当它被移除或者设为可见时,浏览器不会重新渲染,而是会应用缓存,所以对于需要频繁切换显示隐藏的元素,这个属性能够极大地提高渲染性能。
contain-intrinsic-size 可以为元素指定以下一个或两个值。如果指定了两个值,则第一个值适用于宽度,第二个值适用于高度。如果指定单个值,则它适用于宽度和高度。
contain-intrinsic-widthcontain-intrinsic-height
<template><div class="card_item"><div class="card_inner"><img :src="book.bookCover" class="book_cover" /><div class="card_item_right"><div class="book_title">{{ `${book.bookName}${index + 1}` }}</div><div class="book_author">{{ book.catlog }}</div><div class="book_tags"><div class="book_tag" v-for="(item, index) in book.tags" :key="index">{{ item }}</div></div><div class="book_desc">{{ book.desc }}</div></div></div></div>
</template><script setup lang="ts">
import { toRefs } from "vue";const props = defineProps<{book: any;index: any;
}>();
const { book, index } = toRefs(props);
</script><style lang="less" scoped>
.card_item {margin: 20px auto;content-visibility: auto;contain-intrinsic-size: 200px;
}
</style>
相关文章:

两行CSS让页面提升渲染性能
content-visibility是CSS新增的属性,主要用来提高页面渲染性能,它可以控制一个元素是否渲染其内容,并且允许浏览器跳过这些元素的布局与渲染。 content-visibility: hidden的效果与display: none类似其区别在于: content-visibi…...
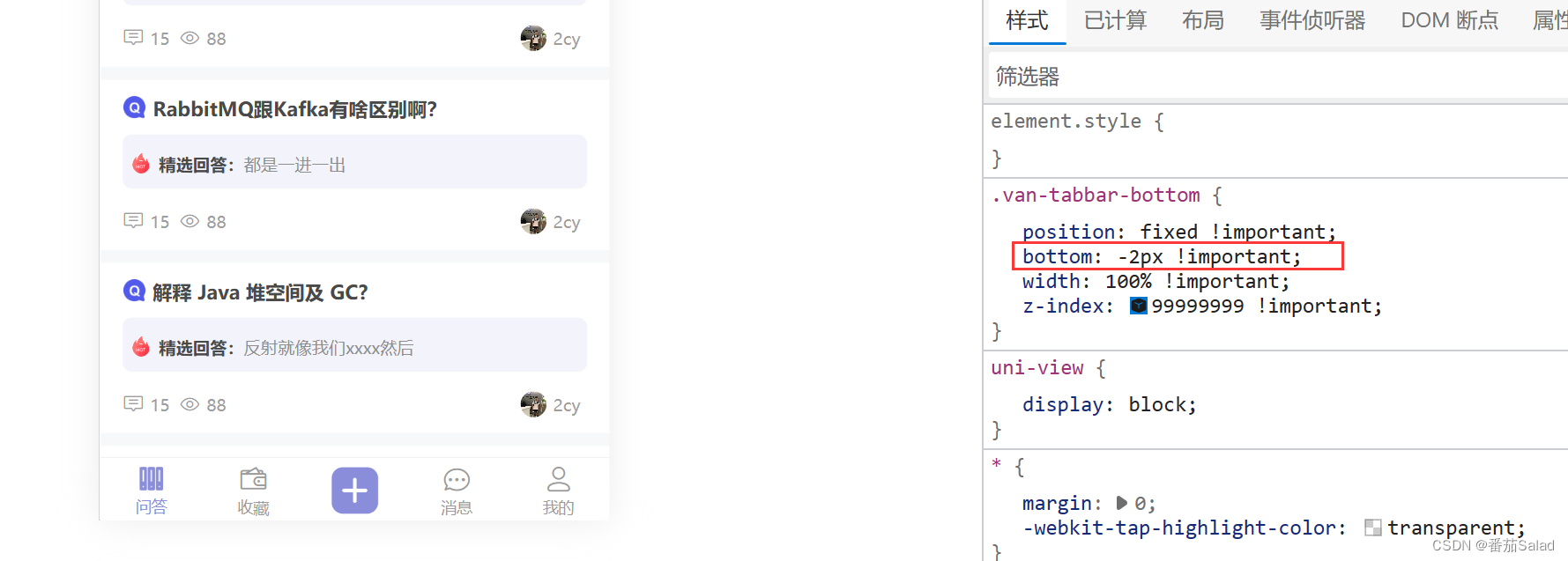
UniApp中tabbar设置了position: fixed以及bottom:0后出现一条缝隙,看到了后面的内容
问题描述 解决方法 直接将bottom设置成-2px即可...

设计模式行为型——责任链模式
目录 什么是责任链模式 责任链模式的实现 责任链模式角色 责任链模式类图 责任链模式举例 责任链模式代码实现 责任链模式的特点 优点 缺点 使用场景 注意事项 实际应用 什么是责任链模式 责任链模式(Chain of Responsibility Pattern)又叫职…...

Xamarin.Android中Intent的使用
目录 1、说明2、使用方法2.1 常用方法2.2 调用系统应用 3、参考资料 1、说明 在Android开发中常常会用到Intent进行不同活动启动,整理资料如下 2、使用方法 2.1 常用方法 1、一般情况而言,都是使用如下的方式进行调用 Intent intent new Intent(th…...

matplotlib绘制方波圆周分解动画
1 方波的圆周分解 在学习傅里叶变换的时候,有一个经典的示例是方波的分解。我们知道,方波可以分解为无数个正弦波的叠加。而正弦波,又可以看作是圆周运动在一条直线上的投影。当时为了理解这个事情,恐怕大家也花了不少时间。 学…...

vue3+ts 实现枚举
首先 index.ts 中定义枚举 export const fruit [{key:1,name:苹果,},{key:11,name:草莓},{key:5,name:香蕉,},{key:51,name:葡萄,},{key:6,name:橙子},{key:7,name:哈密瓜},{key:10,name:西瓜}, ]; 接口返给的数据是一个对象 feeMap{ 1:200, 2&…...

【Python】5分钟了解11个最佳的Python编译器和解释器
11个最佳Python编译器和解释器 1. Brython2. Pyjs3. WinPython4. Skulpt5. Shed Skin6. Active Python7. Transcrypt8. Nutika9. Jython10. CPython11. IronPython结论原文链接 Python是一门初学者的编程语言。它是一种高级语言,非常灵活、解释性和面向对象的语言。…...
如何安装、部署、启动Jenkins
一、测试环境 Linux系统 Centos 7 二、安装步骤: 1、安装jdk 我安装的是jdk8,此处就不多说了,自己百度哈,很简单 2、安装jenkins 首先依次执行如下三个命令: 2.1、导入镜像: [rootcentos7 ~]# sudo …...

sqlalchemy flask长时间未使用 导致数据库连接失效
临时解决方案:在正式运行定时任务之前,先跑一个session.query(),相当于唤醒连接。 参考 https://blog.csdn.net/sinat_42483341/article/details/103723691...

Ubuntu 20.04 系统或图像界面卡死或完全无响应处理方法
Ubuntu 20.04 系统或图像界面卡死或完全无响应处理方法 问题背景无需重启方法安全重启方法 问题背景 Ubuntu 20.04在安装驱动程序时系统突然无响应,终端也无法运行;考虑到尽量不破坏系统,不希望强制上下电重启机器,以免损坏文件系…...
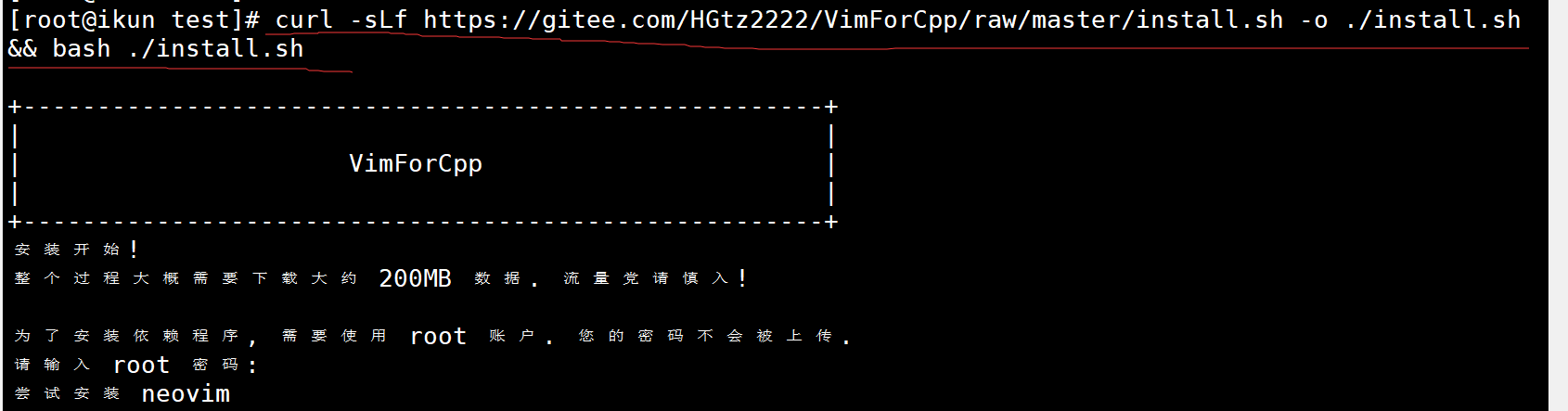
Linux编辑器 - vim使用
1.vim的基本概念 Vim是一个广泛使用的文本编辑器,它是在Unix和Linux系统中常用的命令行文本编辑器之一。 vim的主要三种模式 ( 其实有好多模式,目前掌握这 3 种即可 ), 分别是 命令模式 ( command mode )、 插入模式 ࿰…...

【Windows】磁盘快捷修复
【Windows】磁盘快捷修复 1、背景2、关于Chkdsk3、示例 1、背景 前段时间使用U盘拷贝文件过程中,突然发现U盘无法读取了,U盘里面存储的数据也无法获取。 然后使用windows系统的chkdsk命令进行修复。 chkdsk全称:checkdisk,即磁盘…...
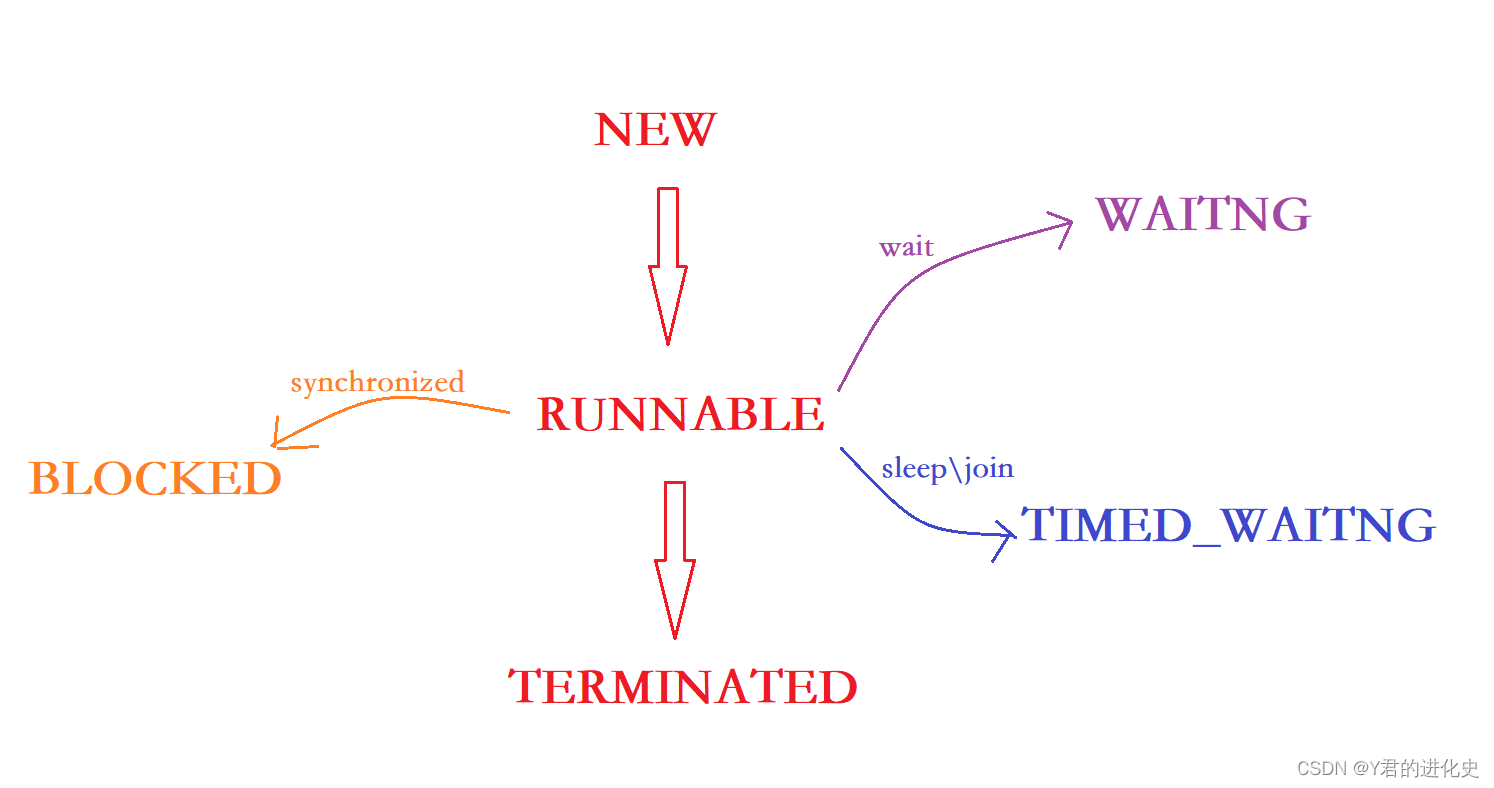
Java 线程的多种状态
前言 在前文中详细介绍了线程的启动、中断、休眠、等待。本文详细介绍线程的多种状态。 获取线程的当前状态代码是: 线程对象.getState(); 目录 前言 一、NEW 二、RUNNABLE 三、BLOCKED 四、WAITNG 五、TIMED_WAITNG 六、TERMINATED 结语 一、NEW Thread 对…...

AI绘画| 迪士尼风格|可爱头像【附Midjourney提示词】
Midjourney案例分享 图片预览 迪士尼风格|可爱头像 高清原图及关键词Prompt已经放在文末网盘,需要的自取 在数字艺术的新时代,人工智能绘画已经迅速崭露头角。作为最先进的技术之一,AI绘画结合了艺术和科学,开启了一…...

【浪费了我两个小时时间】Microsoft store无法加载页面0x80131500
绕的圈,踩的坑 谷歌搜索, newbing搜索都叫我清理缓存,重新安装等方法。 还被这篇文章误导了一下:微软应用商店错误代码0x80072EFD怎么办?(已解决) 加上重启电脑各种试不行。 最后想到要去改代…...

【动态规划】子序列系列
文章目录 动态规划(子序列系列)1. 最长递增子序列2. 摆动序列3. 最长递增子序列的个数4. 最长数对链5. 最长定差子序列6. 最长的斐波那契子序列的长度7. 最长等差数列8. 等差数列划分 || - 子序列 动态规划(子序列系列) 1. 最长递…...

URL存储解锁数据管理的新思路,重新定义数据传输与共享(@vue/repl)
Thinking系列,旨在利用10分钟的时间传达一种可落地的编程思想。 近日,在了解 vue/repl 相关内容,其通过 URL 进行数据存储,感觉思路惊奇,打开了新方式。 首先,通过 URL 存储最大的便利是:无需服…...

matlab程序中文乱码
不同版本的matlab共存在GBK(即,ANSI)和UTF-8两种编码方式,因此可能会出现乱码问题。 第一步:在matlab的命令行窗口输入指令,查看当前编码方式 feature(locale) 第二步:用Notepad打开文件&…...
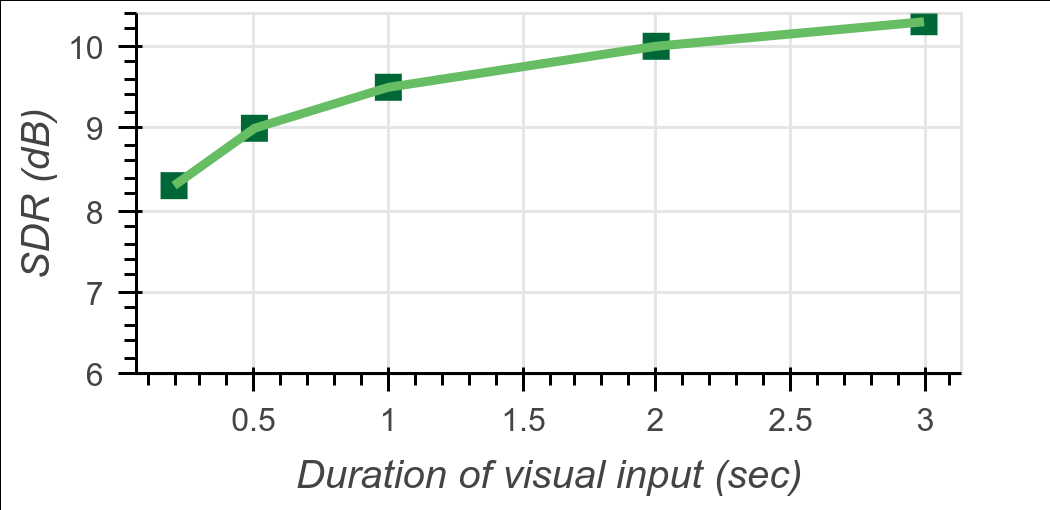
【计算机视觉|语音分离】期望在嘈杂环境中聆听:一个用于语音分离的不依赖于讲话者的“音频-视觉模型”
本系列博文为深度学习/计算机视觉论文笔记,转载请注明出处 标题:Looking to Listen at the Cocktail Party: A Speaker-Independent Audio-Visual Model for Speech Separation 链接:Looking to listen at the cocktail party: a speaker-in…...

curl 介绍和使用
文章目录 一、介绍1.1 curl 介绍1.2 curl 参数介绍1.3 类似Curl的工具和库 二、使用2.1 curl 下载2.2 curl 示例用法2.3 curl命令使用digest方式验证用户 一、介绍 1.1 curl 介绍 官网:https://curl.se/GitHub源码:https://github.com/curl/curl Curl…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...
