05-向量的意义_n维欧式空间
线性代数
什么是向量?究竟为什么引入向量?
-
为什么线性代数这么重要?从研究一个数拓展到研究一组数
-
一组数的基本表示方法——向量(Vector)
-
向量是线性代数研究的基本元素
-
e.g. 一个数: 666, 一组数(6, 66, 666)
-
一组数有什么用?最基本的出发点:表示方向, 这也是向量中为什么包含“向”这个字
-
比如:
-

-
我们从同一个起始点出发同样走了5000米, 我们的方向有偏差,所以最终得到的终止点是不一样的, 三维空间更是同理, 在物理中, 位移, 速度, 加速度, 力。。。 都是有方向这个概念的, 我们只看它的大小是不够的, 是片面的, 我们为了准确的看到这些物理量它所表示的真实的物理含义, 我们必须要考虑它的方向。
-

-
在坐标系中我们一般以0点为原点, 不同起始点之间, 其实对于两个不同起始点来说,它们的区别在于坐标系的不同。换句话说, 这两个过程的不同只在于我们到底认为哪里是原点的不同。
-
向量只表征从一个点到另外的一个点,相应的这样的一个结果而不区分。这个过程是从哪一个起始点出发的,所以为了研究方便, 我们的这个起始点统一都是理解成从原点开始的。
-
在这里提醒一点,对于向量来说,由于它是由多个数字来表示,这多个数字的顺序是重要的,这非常好理解。很显然,(4, 3)这两个数字。所表示的这个向量和(3, 4)是截然不同的,换句话说,向量它也是一组有序的,向量顺序不同,所代表的向量就不同,
-
如果只是表示方向, 最多三个维度就够了
我们之所以引入向量这个概念,换句话说,我们之所以要用一组数来表达我们真实世界中的一些事物,正是因为具有方向这个概念,但是如果我们真的只是表达物理世界中的方向,这个概念的话。其实我们最多使用三个维度就够了,这是因为我们的世界在我们人类自己的感知中是一个三维的空间的世界,任何一个有形的方向最多。都只能在三维的空间中,但是为了扩大我们的研究范围,同时呢,也是为了增强向量这样的一个数学概念,它的能力我们完全可以更加抽象的用向量来描述n维的世界,也就是引入所谓n维向量这样的一个概念。
- 更加抽象的描述n维向量
- 举个栗子:

- 在这里呢?同志们应该明确一个概念,我们是无法直观的感知四维空间或者五维空间它是什么样子的,我们是看不见,也画不出来这样的一个空间的,我们只能去抽象的理解它。
- 但其实我们抽象的用高维的空间来表达一个事物这并不是一个什么特别罕见的,特别稀有的事情。实际上,我们经常这么做,我们在刻画一个事情的时候,经常说我们要从不同的角度来刻画这个事物,那么在这里我们日常用语中所谓的不同的角度,其实就是不同的维度。比如说我们刻画一个房子,我们就可以从这些角度来刻画它,它的面积有多大呀?它有多少个卧室啊?多少个卫生间啊?那么这个房子它具体的地点离最近的地铁站有多远呀?有多少干米?包括这个房子最终的价格到底是多少万元?那么这里每一个数字其实都是一个维度。同志们,我们可以想象不同的房子,相应的对应这些数字就不同,所以我们的每个房子就都可以使用这样的五个数字来表示。换句话说,我们使用了一个五个维度的向量来刻画一个个的房屋,那么这就是一个五维的向量。在这种情况下。显然,向量它其实就是一组数。
- 在这里同志们注意向量所表达的这一组数,它依然是有序的。我们调换一下数字的顺序,它所表达的这个房子的特性就完全不一样,比如说我把这里最后这两个数2和666调换一下,那么它其实就变成了表示有一个房子依然是120平米,三个卧室,两个卫生间,但是距离最近的地铁站有666干米,它的售价呢?仅为两万元,这样的一个房子和这里的这个房子是截然不同的。那么当然了,向量就是一组数, 这组数的含义本身其实是由使用者来定义的。
- 其实同志们想象一下,我们之前所介绍的我们用向量来表示方向。其实两个维度也好,三个维度也好,每一个维度代表哪个方向也是由我们使用者来定义的,只不过通常呢,我们就直接使用xyz这样的顺序来定义它而已,那么不管怎样,我们可以看出来,向量都是一组有序的数字,我们可以用两个视角来看待它,一个视角,我们就把它看作是一个方向。
- 当然在这里,我只说方向稍有不准确,其实这个方向的背后也蕴含了大小,因为(4, 3)和(8, 6)。其实它们指向的是同一方向,但是大小不同
- 两个视角看似不同, 但可以互相转换
- 一个方向, 就是一个点
- 空间中的一个点, 可以看做从原点指向这个点的一个方向。
- 下面来说一下另外一个视角, 另外一个视角呢?看起来它似乎不是表示一个方向,仅仅是一组有序的数字,那么对于这一组有序的数字,我们可以把它理解成是一个在高维空间中的数据点,
- 换句话说,大家可以想象一下,对于这个五维向量,我们可以想象成有个拥有五个维度坐标轴的这样的一个空间。那么,每个维度的坐标轴的取值都可以从负无穷到正无穷,在这之间呢,进行任意的取值,那么我们当前的这个房子就对应这五个维度,分别是取这些值所对应的一个点,那么一旦我们使用这样的视角来看待以后。其实这两个视角儿就可以互相转换了,这是因为一个方向和一个点是一一对应的,我们在之前介绍方向的时候。
- 就已经提出这一点了,由于在我们线性代数的世界中考虑方向这个概念,它的起始点并不重要,都是从原点出发的。所以对于空间中的任何一个点来说,我们都可以把它直接看作成一个从原点指向这个点的一个方向。也就是说,对于这个五维向量(120, 3, 2, 2, 666)来说,我们可以把它看作是从5个零,也就是五维空间中的那个坐标原点。指向这样的一个点的一个方向,当然了,同理对于这个从(0, 0)到(4, 3)的这个方向来说,我们也可以非常简单的只用(4, 3)这一个坐标点来进行表示。这二者呢, 其实是等价的
向量与其运算
向量是线性代数里面最基本的概念,它其实就是一维数组,由 N 个数构成的, X=(X1, X2…Xn)
向量的维度可以是任意正整数,可以表示在 n 维空间中的位置或方向。向量本身是一维的, 但向量所处的空间是n维的
向量的几何意义就是空间中的点,物理意义速度或者力这样的矢量,

向量的分量数我们称之为向量的维度(也可以称为特征Feature),n 维向量集合的全体就构成了 n 维欧式空间, R^n
向量的分量数也称为向量的维度。在数学中,一个向量的维度是指向量在空间中的自由度或维数。一个 n 维向量表示在 n 维空间中的一个点或位置,它可以用 n 个分量来表示,分别对应该向量在每个坐标轴上的投影。
例如,在二维空间中,一个向量有两个分量,分别表示在 x 轴和 y 轴上的投影,因此称为二维向量。在三维空间中,一个向量有三个分量,分别表示在 x 轴、y 轴和 z 轴上的投影,因此称为三维向量。以此类推,向量的维度可以是任意正整数。
向量的维度决定了向量的空间位置和方向的自由度,也决定了向量在数学运算中的规则和特性。不同维度的向量在运算和表示上会有一些差异,但它们都符合向量的基本定义和性质。
如果一个向量是 (2, 3),那么它的分量就是两个值:2 和 3。在二维空间中,一个向量有两个分量,分别对应它在 x 轴和 y 轴上的投影。
在这个例子中,向量 (2, 3) 表示在 x 轴方向上有一个分量为 2 的投影,在 y 轴方向上有一个分量为 3 的投影。这样的向量可以用来表示平面上的一个点或位置。在笛卡尔坐标系中,向量 (2, 3) 从原点出发,沿着 x 轴方向移动 2 个单位,然后沿着 y 轴方向移动 3 个单位,最终到达点 (2, 3)。
需要注意的是,向量的分量的顺序通常是按照笛卡尔坐标系的顺序排列,即先是 x 轴方向的分量,然后是 y 轴方向的分量。因此,(2, 3) 表示的是 x 轴方向的分量为 2,y 轴方向的分量为 3。
- 在学习初始, 使用方向的视角, 更直观, 更形象
- 我们在实际的使用线性代数的过程中,我个人认为我们更多的是倾向于使用第二个视角来看待向量,也就是把每一个向量看作是空间中的一个点,但是在我们学习向量的基本性质的时候,很多时候我们使用方向这样的一个视角去看待,会更加的容易,这是因为我们可以直接在二维的世界中,或者三维的世界中绘制出这个向量来,然后非常直观的看到。这个向量具体是什么样子的?相应的一些运算对于这个向量会产生什么样的影响?那么通过这样的一个直观的学习之后,我们可以把我们学到的这些运算也好,性质也好。也好推广到更高维的维度向量空间中去,这本身呢,也是我们在学习线性代数的过程中的一个非常基本的学习方法。
- 那么,在这里,同志们要注意的是,不管这两种视角使用哪个视角,在这里,向量其实都并不是简单的一组数而已,它并不是把这些数字扔在那里排列起来,我们在看待向量的时候,是把它和空间联系起来的。对于第一个视角儿,我们说。向量是具有方向的,其实我们把它看成了一个有向的线段,而对于第二个视角儿,我们把它看成了是空间中的一个点。这两个视角儿都具有一定的几何意义,而不仅仅是数学上数字的堆叠而已。对于此,我希望同志们有所理解,在我们的学习中,一旦同志们认为。某一些概念太抽象了的话,其实我们就可以去尝试着把这个概念进行具象化,比如说就看在三维空间中,甚至是二维空间中。在这样的一个几何空间中。它到底意味着什么?这将非常有助于同志们理解线性代数中的很多计算的过程,甚至是非常复杂的概念。
相关文章:

05-向量的意义_n维欧式空间
线性代数 什么是向量?究竟为什么引入向量? 为什么线性代数这么重要?从研究一个数拓展到研究一组数 一组数的基本表示方法——向量(Vector) 向量是线性代数研究的基本元素 e.g. 一个数: 666,…...

交通运输安全大数据分析解决方案
当前运输市场竞争激烈,道路运输企业受传统经营观念影响,企业管理者安全意识淡薄,从业人员规范化、流程化的管理水平较低,导致制度规范在落实过程中未能有效监督与管理,执行过程中出现较严重的偏差,其营运车…...
)
vimrc 配置 (持续跟新中)
vimrc 配置 #显示行号 set nu #自动换行 set autoindent #设置tab键 宽度为四个空格 set tabstop4 set shiftwidth4 set expandtab更多文章,详见我的博客网站...

【集成学习介绍】
1. 引言 在机器学习领域,集成学习(Ensemble Learning)是一种强大的技术,通过将多个弱学习器组合成一个更强大的集成模型,来提升模型的鲁棒性和性能。 2. 集成学习的原理 集成学习的核心思想是“三个臭皮匠ÿ…...

动画制作选择Blender还是Maya
Blender和Maya是两种最广泛使用的 3D 建模和动画应用程序。许多经验丰富的用户表示,Blender 在雕刻工具方面远远领先于 Maya,并且在 3D 建模方面达到了相同的质量水平。对于刚接触动画行业的人来说,您可能会问“我应该使用 Blender 还是 Maya…...
215. 数组中的第K个最大元素
题目链接:力扣 解题思路: 方法一:基于快速排序 因为题目中只需要找到第k大的元素,而快速排序中,每一趟排序都可以确定一个最终元素的位置。 当使用快速排序对数组进行降序排序时,那么如果有一趟排序过程…...

NLP From Scratch: 生成名称与字符级RNN
NLP From Scratch: 生成名称与字符级RNN 这是我们关于“NLP From Scratch”的三个教程中的第二个。 在<cite>第一个教程< / intermediate / char_rnn_classification_tutorial ></cite> 中,我们使用了 RNN 将名称分类为来源语言。 这次ÿ…...

Spring MVC程序开发
目录 1.什么是Spring MVC? 1.1MVC定义 1.2MVC和Spring MVC的关系 2.为什么要学习Spring MVC? 3.怎么学Spring MVC? 3.1Spring MVC的创建和连接 3.1.1创建Spring MVC项目 3.1.2RequestMapping 注解介绍 3.1.3 RequestMapping 是 post 还是 get 请求? …...
医疗知识图谱问答——文本分类解析
前言 Neo4j的数据库构建完成后,现在就是要实现医疗知识的解答功能了。因为是初版,这里的问题解答不会涉及深度学习,目前只是一个条件查询的过程。而这个过程包括对问题的关键词拆解分类,然后提取词语和类型去图数据库查询…...

JS关于多张图片上传显示报错不影响后面图片上传方法
关于多张图片上传或者下载显示报错后会程序会终止执行,从而影响后面图片上传。 解决方法: /*能正常访问的图片*/ const url https://2vimg.hitv.com/100/2308/0109/5359/dqKIZ7d4cnHL/81Vu0c.jpg?x-oss-processimage/format,webp; /*不能正常下载的图…...

MySQL踩坑之sql_mode的用法
目录 定义 报错重现 编辑 原因分析 sql_mode值说明 查看当前sql_mode 设置sql_mode 定义 什么是sql_mode?玩了这么久的MySQL语句...
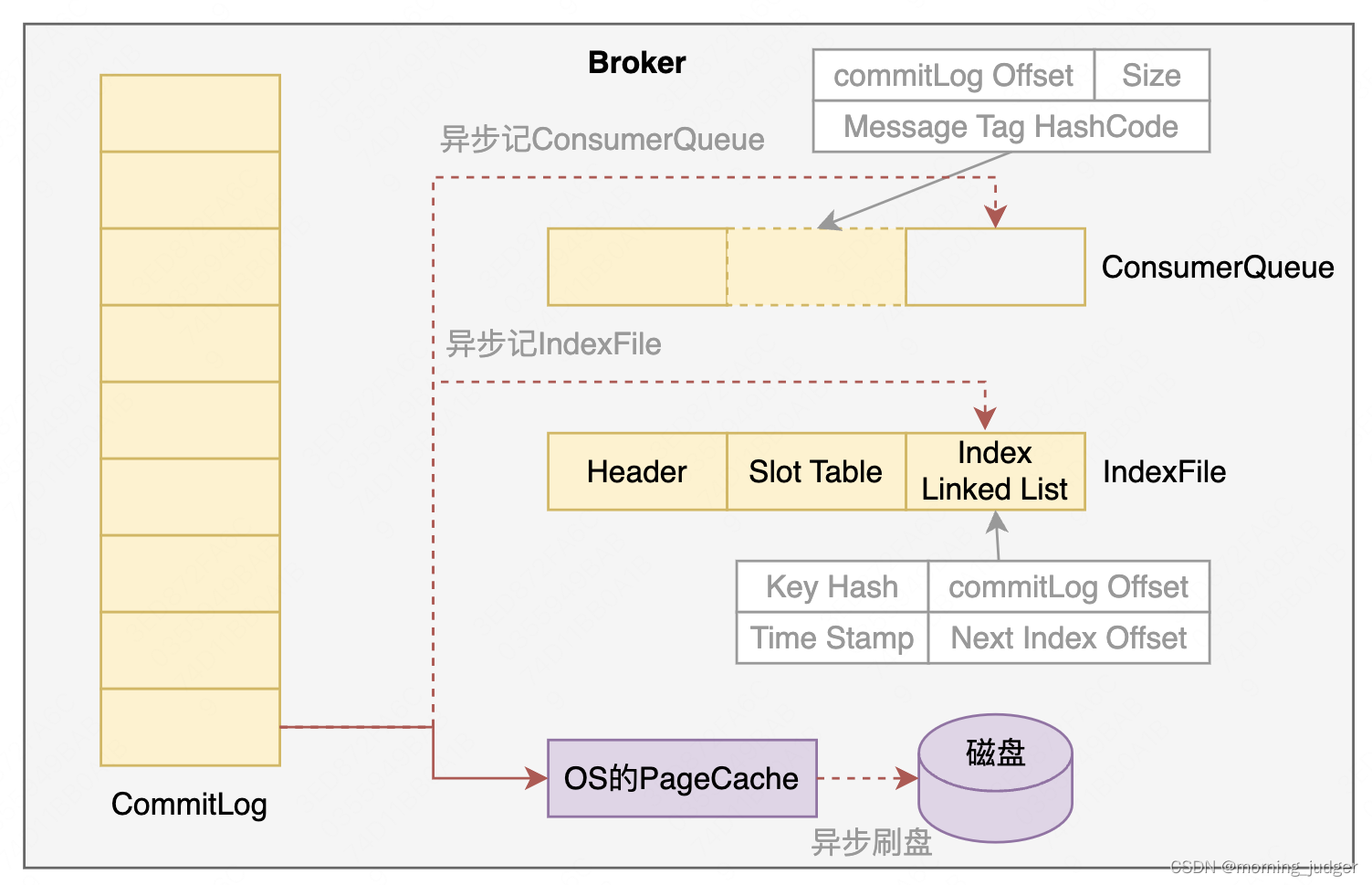
消息队列总结(4)- RabbitMQ Kafka RocketMQ高性能方案
1.RabbitMQ的高性能解决方案 1.1 发布确认机制 RabbitMQ提供了3种生产者发布确认的模式: 简单模式(Simple Mode):生产者发送消息后,等待服务器确认消息已经被接收。这种模式下,生产者发送消息后会阻塞&am…...
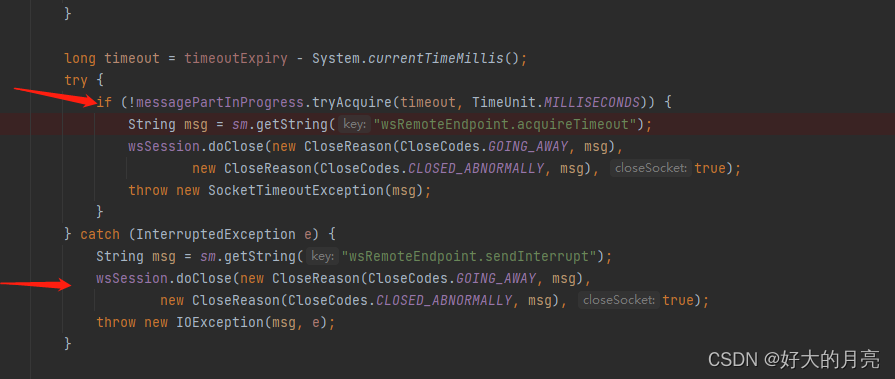
websocket服务端大报文发送连接自动断开分析
概述 当前springboot版本:2.7.4 使用依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dependency>现象概述: 客户端和服务端已经有心跳…...
想写几个上位机,是选择学c#还是 c++ qt呢?
C#基本也就上位机开发开发,另外做做日常用的小工具很方便。 结合PLC,以太网做上位机,这个基本上控制这块都比较有需求。 另外我们用C#也做一些工具的二次开发,感觉还行。 C用qt框架其实学习起来可能稍微复杂些,但是…...

JavaScript 简单实现观察者模式和发布-订阅模式
JavaScript 简单实现观察者模式和发布-订阅模式 1. 观察者模式1.1 什么是观察者模式1.2 代码实现 2. 发布-订阅模式2.1 什么是发布-订阅模式2.2 代码实现2.2.1 基础版2.2.2 取消订阅2.2.3 订阅一次 1. 观察者模式 1.1 什么是观察者模式 概念:观察者模式定义对象间…...
java集成短信服务 测试版 qq邮箱简单思路
java集成短信服务 注册一个帐号 使用的是容联云,百度搜一下官网 用手机注册一个帐号就行,免费体验不需要认证 注册后会有八块钱送,可以使用免费的给自己设置三个固定手机号发送短信,不需要认证。 此页面的 三个信息需要在代码中…...
#P0994. [NOIP2004普及组] 花生采摘
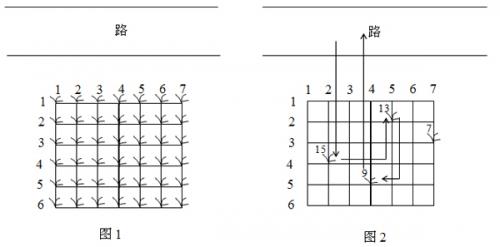
题目描述 鲁宾逊先生有一只宠物猴,名叫多多。这天,他们两个正沿着乡间小路散步,突然发现路边的告示牌上贴着一张小小的纸条:“欢迎免费品尝我种的花生!――熊字”。 鲁宾逊先生和多多都很开心,因为花生正…...
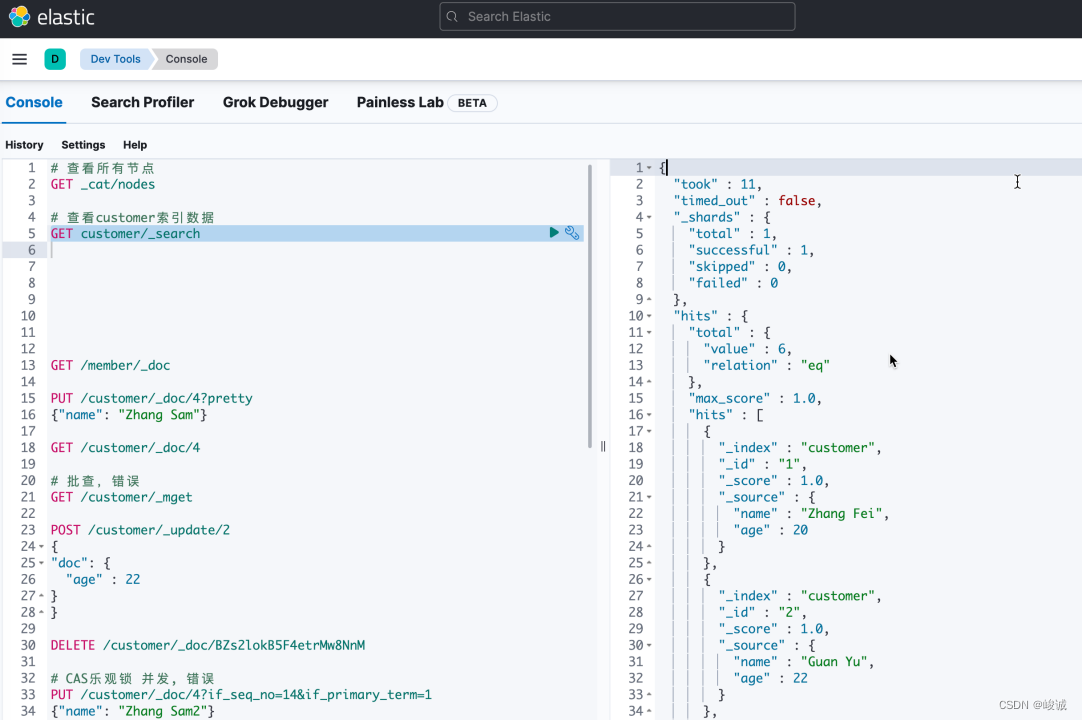
Elasticsearch和Kibana的安装及验证
金翅大鹏盖世英,展翅金鹏盖世雄。 穿云燕子锡今鸽,踏雪无痕花云平。 ---------------- 2023.7.31.101 ----------------- 本文密钥:365 Elasticsearch 是一个分布式的 RESTful 风格的搜索和数据分析引擎,常用来进行全文检索、…...
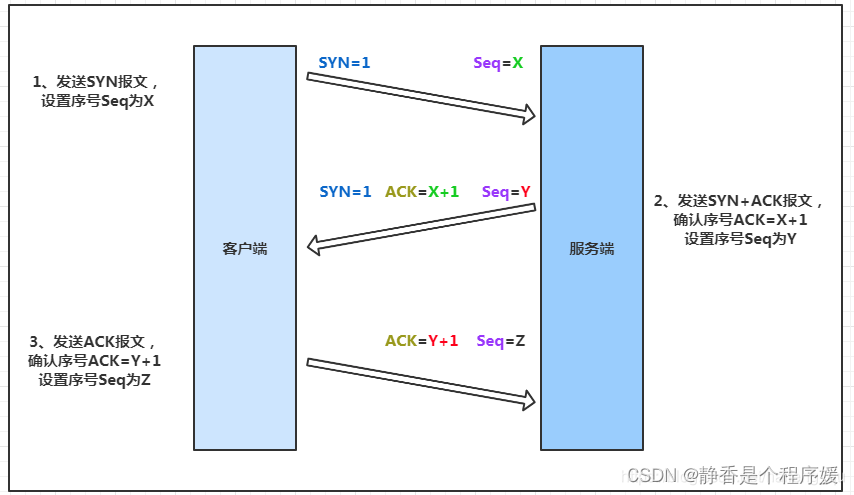
细讲TCP三次握手四次挥手(一)
计算机网络体系结构 在计算机网络的基本概念中,分层次的体系结构是最基本的。计算机网络体系结构的抽象概念较多,在学习时要多思考。这些概念对后面的学习很有帮助。 网络协议是什么? 在计算机网络要做到有条不紊地交换数据,就必…...

【linux-zabbix】zabbix-agent启动报错:Daemon never wrote its PID file. Failing.
背景: 发现有部分的agent失联,排查发现机器正常,agent没起来。 排查日志发现: # journalctl -xe -- Support: http://lists.freedesktop.org/mailman/listinfo/systemd-devel -- -- Unit zabbix-agent.service has begun start…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
