雅利安人覆灭了世界三大文明,为何单单在商朝被斩首两万?
转自:雅利安人覆灭了世界三大文明,为何单单在商朝被斩首两万? (baidu.com)
在公元前3000年至1000年的广大时间内,是世界四大文明古国大放光彩的时候,古印度文明、古巴比伦文明、古埃及文明以及我们的古华夏,他们都为世界留下了一笔非常丰富的宝贵财富。
然而也正是在这一段时间之内,曾经大方光芒的四大文明居然接二连三的消失,最后只剩下了一个中华文明一直持续绽放光芒,时至今日,中华文明成为了华夏的宝藏。
不过在当时真的可是千钧一发,因为世界三大文明的消失都和一个古老的民族有关,这个民族叫:雅利安。
雅利安人是个什么存在?
雅利安人是一群什么人,现在的历史始终不能解答疑惑,不过大部分人的认知是雅利安人是生活在俄罗斯乌拉尔山脉草原上的一个古老游牧民族,在当时经过大规模迁徙然后到达了阿姆河和锡尔河之间,这群人被称为雅利安—旁遮普人。
在公元前14世纪的时候,旁遮普人大举南下进入了南亚次大陆,在这里他们创造了吠陀文化和建立了种姓制度,而到这我们就知道这里是哪里了。
那么我们到这就要问了,雅利安人本来在那块土地上生存的挺好的,每天小酒喝着,小日子过着,就算是以游牧为生的牧民也不会这样大规模的流动,相反他们都是有固定草场的,每到一个季节就会流动到下一个草场去,怎么会经过长达数千里的跋山涉水呢?

而这就要提及当时的一段历史了:公元前3000年左右,世界历史进入了小冰河时期,全球气温骤然下降,严寒的恶劣天气让生活变得更加艰难。
雅利安人原本是靠放牧生活的,可是突如其来的严寒让他们不得不放弃原有的生活,而且雅利安的居住地本身就靠近北极圈附近,所以比起其他地方更加的艰难。
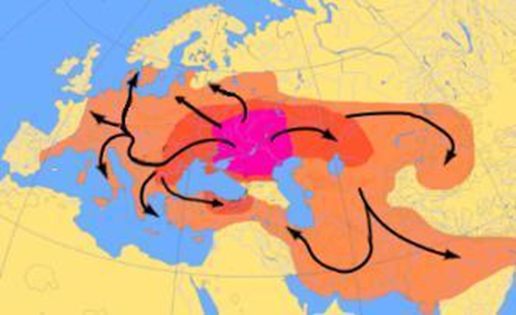
在经历了这次“小冰河时代”之后,雅利安人发现原来的地方已经不适合自己居住了,因此在当时不得不进行大规模的迁徙,而雅利安的这个举动一不小心就改变了历史。

雅利安人覆灭三大文明
在当时人们还没有“融合”这个概念,很多的民族都是在自己的一亩三分地上各自繁衍生息,可以说当时的人都是很“排外的”,因此雅利安人在迁徙的过程之中也遇到了不小的阻力。
雅利安人在迁徙的过程之中也并非都往一个地方,其中他们有一支进入了伊朗高原,迁徙到这里的雅利安人和当地的米底人在经过了一番相爱相杀之后便进行了融合,而这个地方后来产生了一个强大的国家:古波斯帝国。
在波斯帝国的旁边,当时有着一个“古巴比伦王国”,波斯帝国在对外扩张的过程之中不免和古巴比伦王国相遇,久而久之两个国家之间就有了摩擦,最后这就成为了不可磨灭的仇恨,两方之间开始大打出手。
波斯帝国的第一代首领居鲁士在生前就已经大大打击了古巴比伦王国的有生力量,而到了他的儿子居鲁士二代,波斯帝国继续在对外扩张,最终古巴比伦王国被雅利安踩在脚下。
在征服古巴比伦文明之后,居鲁士二世还来不及征服古埃及文明就死了,在他死后,他的儿子就将目光对准了当时地中海对面的古埃及文明。
当时古埃及境内,法老虽然是名义上的统治者,可是当时古埃及境内真正的权贵是古埃及的僧侣们,他们在当时掌握着大量的财富,而面对代表着雅利安文明的波斯人的进攻,法老甚至没有多余的军费来抵抗雅利安,最终古埃及文明落幕,现在埃及的土地上只留下了一座座的“金字塔”,不过是不是那时候建造的就不知道了。

而另外一支雅利安部族则更往南,就如同上文所说其迁徙到了南亚次大陆,同化了原来生活在这里的原住民,并建立了人们熟知的吠陀文明和种姓制度。
至此世界四大文明以灭其三,只剩下中华文明还继续在如今的这片土地之上。
雅利安人曾入侵商朝
其实当时雅利安也曾经想要入侵华夏文明,这一点我们在很多的文献典籍之上都可以看到,可是在当时雅利安最终失败了,那么这是为何呢?
我们华夏人打仗讲究的是天时地利人和,而当时我们地利人和占据优势,雅利安岂有不败之理?
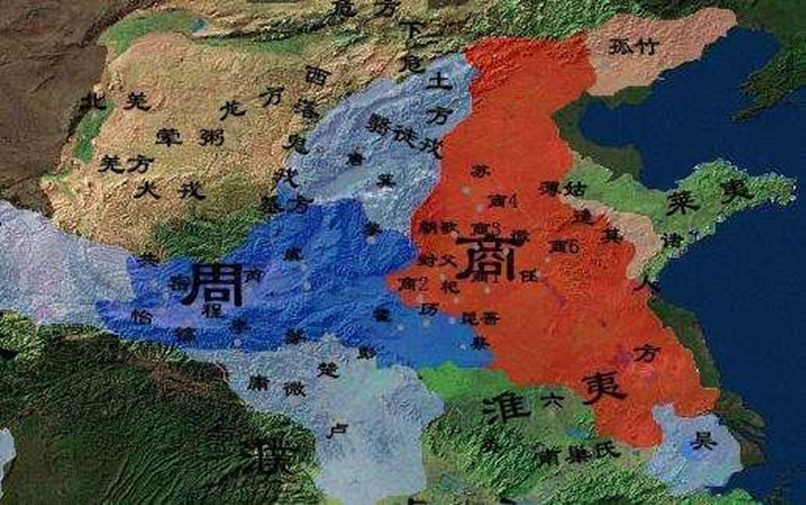
首先我们就说说地利方面吧,我们华夏的地形图很怪,我们拥有960万平方公里的土地,可是却有很多人会说我们的可耕面积还不如旁边一个比我们面积小的国家。
事实上的确是如此,可是如果细看地利会发现,我们的地理具有多么大的优势,在冷兵器时代,西边被喜马拉雅山脉阻隔,在当时人们的认知所限,还没有能力能够翻越那座山,因此那个地方帮助我们阻挡了北方的入侵者。

南面十万大山,十万群山阻隔,外加上各种毒蛇瘴气丛生,对于当地不熟悉的人很容易在这十万大山的瘴气之中全军覆没。
而东边则是一望无际的大海,在大航海时代开启前,人们对于大海的认知是有限的,因此这又阻绝了东边的敌人。
因此在华夏古代,很多时候人们都是将目标放在了北边,因为北边一望无际的戈壁沙漠虽然气候恶劣,可是对于游牧民族来说也是战斗的主场。
因此这特殊的地理位置让华夏文明在很长时间内斗可以免受外来力量的入侵,虽然这地形奇怪,可正是这奇奇怪怪的地理位置孕育了华夏文明。
而除了地利之外,人和也是一个要素,现在我们夸耀一个民族比较能打,我们会以“战斗民族”来称呼他,可是殊不知我们自己更适合用“战斗民族”。

华夏有将近五千年的历史,除了几个大统一王朝之外,华夏的历史还有将近长达2500年的乱世,这其中有一半时间都在打仗。
当时雅利安入侵其他民族的时候,对于雅利安人这种奇奇怪怪的打法很不适应,外加上那些地方大多是平原为主,更是雅利安人的主场。
然而在这片土地上和华夏人玩骑兵战术,那么我们称第二,还真没人敢称第一。
华夏五十六个民族除之中有一半民族都曾经属于游牧民族,骑兵作战是行家里手,更不用说在古代以骑马射猎为生了。
雅利安的骑兵部队来无影去无踪的打法确实是让很多国家叫苦不迭,可是在这里我们还真不怵。

更悲催的是,雅利安入侵时候正好碰上了商朝最强盛的时期武丁时期,他在位期间商朝的国力到达了鼎盛时期,而且当时他还有一位好老婆妇好。
平时武丁在家治国理政,妇好就率领商朝大军外出征战,在当时商朝周边也有不少的游牧民族,比如鬼方、羌方、土方等,这些部族平常也都是靠游牧为生,而妇好常年和他们打仗,因此对付游牧民族对她来说简直就是小菜一碟。
因此这部分入侵商朝的雅利安人在这之后就非常悲剧,直接被妇好打败然后拉去当了奴隶,妇好死后,这部分人直接被拉去殉葬,所以后世我们打开妇好墓的时候发现这里面有一部分人的头骨和我们不同。
相关文章:

雅利安人覆灭了世界三大文明,为何单单在商朝被斩首两万?
转自:雅利安人覆灭了世界三大文明,为何单单在商朝被斩首两万? (baidu.com)在公元前3000年至1000年的广大时间内,是世界四大文明古国大放光彩的时候,古印度文明、古巴比伦文明、古埃及文明以及我们的古华夏,…...

Windows 系统上查询 GPU / CPU 对 Vulkan 的支持信息
Windows 系统上查询 GPU / CPU 对 Vulkan 的支持信息1. TechPowerUp GPU-Z https://www.techpowerup.com/gpuz/ GPU-Z is a lightweight system utility designed to provide vital information about your video card and graphics processor. GPU-Z 是一款显卡识别工具&…...

python3 字节与数字、字符等互转的方法。int、struct库等方法
文章目录int 与 bytes转换int 转 bytesbytes 转 intstr 与 bytes互转其他格式转字节格式说明转字节字节转其他字节在存储的时候根据存储的格式不同,可能会有大端小端之分,如果是数字,还有有符号无符号的区分,所以在自己处理的时候…...
人脸检测的5种方式
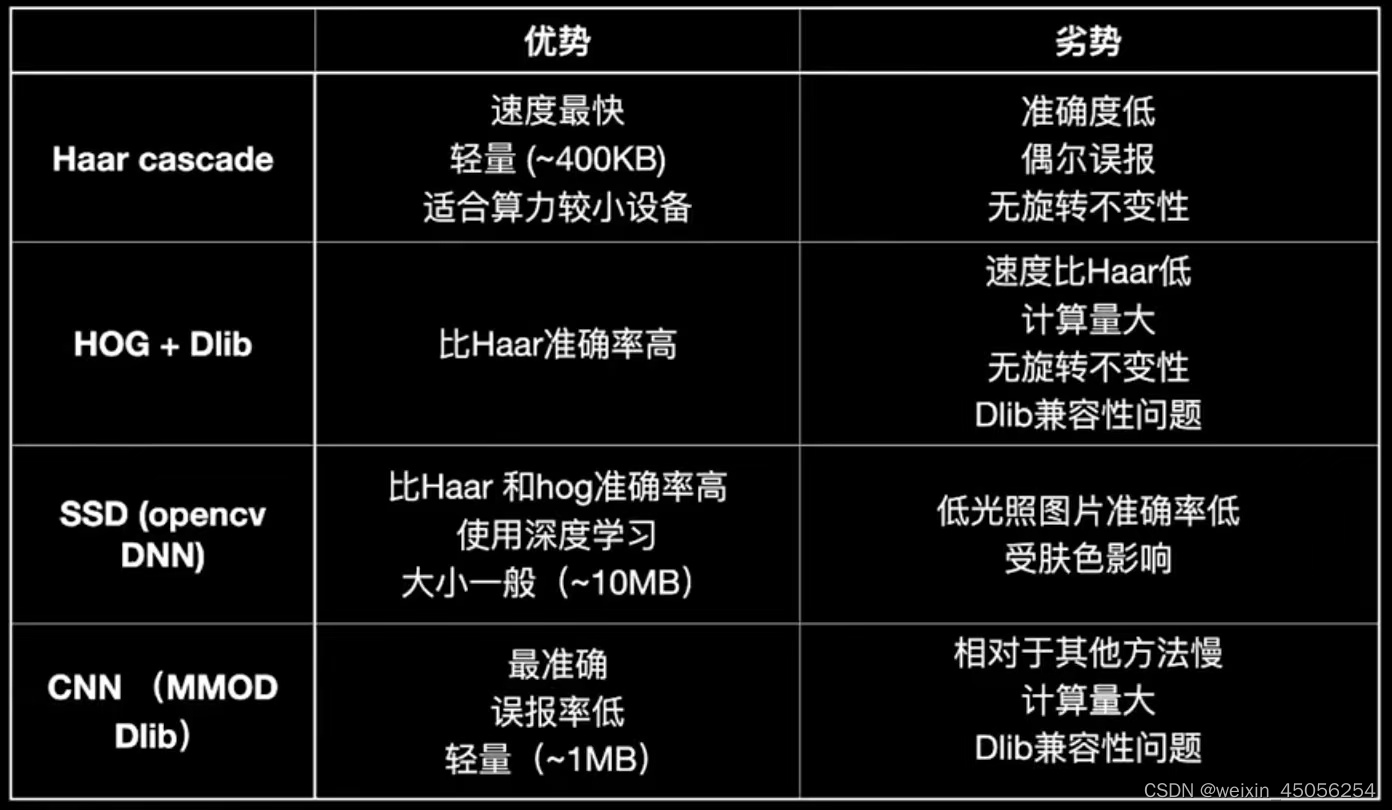
文章内容: 1)人脸检测的5种方法 1. Haar cascade opencv 2. HOG Dlib 3. CNN Dlib 4. SSD 5. MTCNN 一。人脸检测的5种方法实现 1. Haar cascade opencv Haar是专门用来检测边缘特征的。基本流程如下: 第1步,读取图片 img …...
)
华为OD机试 - 乘积最大值(Python)
乘积最大值 题目 给定一个元素类型为小写字符串的数组 请计算两个没有相同字符的元素长度乘积的最大值 如果没有符合条件的两个元素返回0 输入 输入为一个半角逗号分割的小写字符串数组 2 <= 数组长度 <= 100 0 < 字符串长度 <= 50 输出 两个没有相同字符的元…...
【CMU15-445数据库】bustub Project #2:B+ Tree(上)
(最近两个月学校项目有亿点忙,鸽得有点久,先来把 Project 2 补上) 本节实验文档地址:Project #2 - BTree Project 2 要实现的是数据结构课上都会讲的一个经典结构 B 树,但是相信大多数的同学(…...

功率放大器在lamb波方向算法的损伤定位中的应用
实验名称:基于PZT结Lamb波方向算法的损伤定位方法研究方向:损伤定位测试目的:Lamb波是在具有自由边界的固体板或层状结构中传输的一种弹性导波,由于其本身的传播特性,如沿传播路径衰减小,能量损失小&#x…...
时的科技迎1亿融资,这辆“空中的士”能否实现真正飞行?
近期,进行载人eVTOL的研发、生产和销售的时的科技宣布完成1亿元Pre-A轮融资,成立不到两年,这已是时的科技的第三轮融资,此前,时的科技已获得蓝驰创投和德迅投资千万美元种子轮投资。在不少人看来,时的科技所…...

idea 折叠代码块技巧 关于<editor-fold>
最近在使用delombok插件的时候,发现了一个有意思的小技巧 以前用VSstudio写代码的时候。经常使用代码块折叠的方法。但是在写java的时候,没怎么使用过 VSStudio中的写法 即 #region xxx ... your great coding #endregion这样在浏览的时候,…...
python|第五章考试题及练习题
本篇文章是对北京理工大学嵩天老师的《Python语言程序设计》第五章考试题及练习题的学习记录。 一、考试题 1、随机密码生成 问题描述: 描述 补充编程模板中代码,完成如下功能:…...

DIY生日蛋糕笔记
自制6寸生日蛋糕笔记 实验环境: 长帝CRTF32PD搪瓷烤箱32升, 九阳电动打蛋器, 裱花盘一套 蛋糕盒子 称重器 硅胶刀 两个大碗1号和2号。 材料: 参考: https://www.bilibili.com/video/BV1t34y1Z7mL/?spm_id_from333…...
)
MybatisPlus------常用注解和逻辑删除以及设置统一前缀以及主键生成策略(六)
MybatisPlus------常用注解以及设置统一前缀以及主键生成策略(六) 在使用MybatisPlus的过程中时,实力类的Mapper继承BaseMapper,此时不要添加TableName注解也能够对表数据实现增删改查。 // mybatispuls 提供了接口实现单表的增…...

JQuery工具框架
JQuery工具框架 直接使用js编程比较麻烦,而且还必须考虑浏览器的差异性。 为了简化javascript的开发,一些javascript库诞生了。当今流行的javascript库有:jQuery诞生于2005 年,Dojo、 EXT_JS、DWR、YUI… jQuery是John Resig在…...

同一个整型常量怎样在不同进制间之间转换?
整型常量可以分别用二进制、八进制、十进制和十六进制表示,不同的进制并不影响数据本身的大小,同一个整型常量可以在不同进制之间转换,具体转换方式如下。1.十进制和二进制之间的转换(1)十进制转二进制。十进制转换成二进制就是一个除以2取余…...
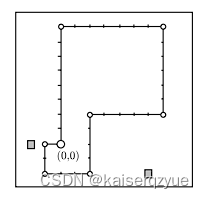
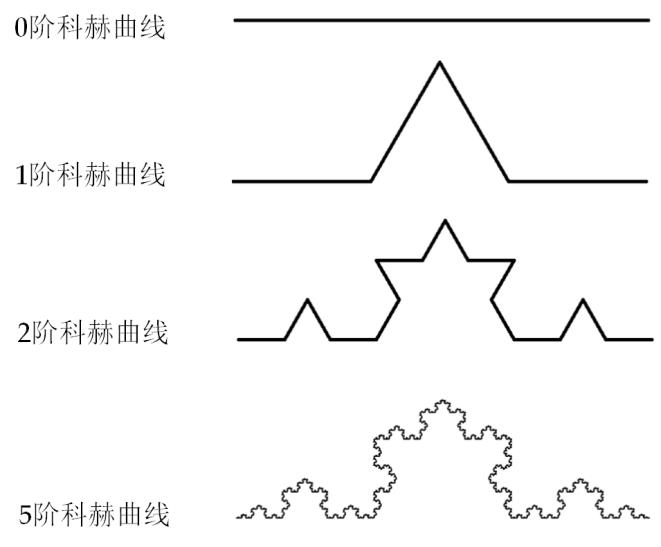
UVa 225 Golygons 黄金图形 暴力搜索 剪枝 状态判断
题目链接:Golygons 题目描述: 给定nnn和kkk个障碍物的坐标,你需要走nnn次,第一次走一个单位距离,第二次走二个单位距离,…,第nnn次走nnn个单位距离。走得过程中不能穿过或者到达障碍物所在的点&…...

PowerShell中的对象是神马?
在PowerShell中,无处不在体现出一个概念,这个概念是什么呢?就是对象,对象是面向对象的语言中非常重要的概念,PowerShell的底层是.net,也是面向对象的语言,因此它也继承了面向对象的语言的语法特性。但是很多人在使用PowerShell 语言的时候会觉得有些疑惑,到底什么是Pow…...
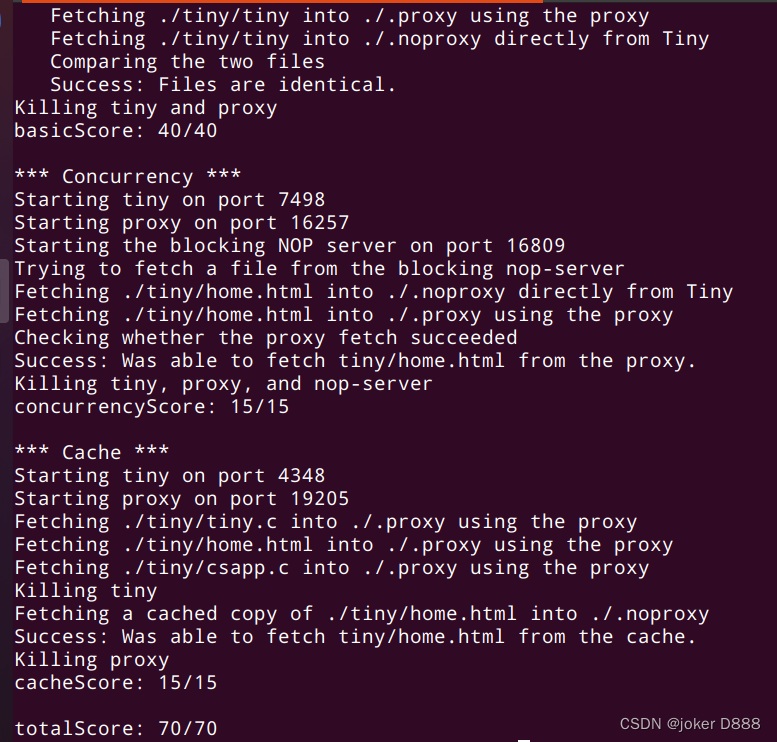
Proxy lab
CSAPP Proxy Lab 本实验需要实现一个web代理服务器,实现逐步从迭代到并发,到最终的具有缓存功能的并发代理服务器。 Web 代理是充当 Web 浏览器和终端服务器之间的中间人的程序。浏览器不是直接联系终端服务器获取网页,而是联系代理&#x…...

【机器学习】Sklearn 集成学习-投票分类器(VoteClassifier)
前言 在【机器学习】集成学习基础概念介绍中有提到过,集成学习的结合策略包括: 平均法、投票法和学习法。sklearn.ensemble库中的包含投票分类器(Voting Classifier) 和投票回归器(Voting Regressor),分别对回归任务和分类任务的…...

Day892.MySql读写分离过期读问题 -MySQL实战
MySql读写分离过期读问题 Hi,我是阿昌,今天学习记录的是关于MySql读写分离过期读问题的内容。 一主多从架构的应用场景:读写分离,以及怎么处理主备延迟导致的读写分离问题。 一主多从的结构,其实就是读写分离的基本…...

无线蓝牙耳机哪个品牌音质好?性价比高音质好的蓝牙耳机排行榜
其实蓝牙耳机购买者最担忧的就是音质问题,怕拿到手的蓝牙耳机低频过重又闷又糊,听歌闷耳的问题,但从2021年蓝牙技术开始突飞猛进后,蓝牙耳机的音质、连接甚至是功能都发生了很大的变化,下面我分享几款性价比高音质的蓝…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...
