二叉搜索树(BST)的模拟实现
序言:
构造一棵二叉排序树的目的并不是为了排序,而是为了提高查找效率、插入和删除关键字的速度,同时二叉搜索树的这种非线性结构也有利于插入和删除的实现。
目录
(一)BST的定义
(二)二叉搜索树操作
1、BST的查找
2、BST的插入
3、BST的删除
(三)二叉排序树的实现(非递归)
1、查找实现
2、插入实现
3、删除实现
(四)二叉排序树的实现(递归)
1、查找操作
2、插入操作
3、删除操作
(五)其他操作
1、析构
2、构造和拷贝构造
3、赋值重载
(六)总结
(一)BST的定义
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树

(二)二叉搜索树操作
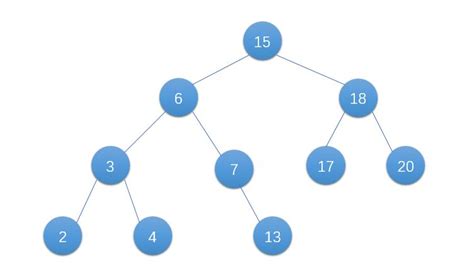
我以下图这棵二叉树为例,给大家进行有关二叉树操作的讲解:

1、BST的查找
思想:
- 二叉搜索树的查找是从根节点开始的,沿某个分支逐层的向下比较的过程;
- 若二叉排序树非空,先将给定值与根节点的关键字进行比较,若相等则查找成功;
- 若不等,如果小于根节点的关键字,则在根节点的左子树上进行查找;
- 否则,就在根节点的右侧进行查找。这显然是一个递归的过程!!
举例:
- 例如,对于上述二叉树我想要查找值为【6】的结点。
- 首先 6 与根节点 8 进行比较,由于 6<8 ,因此需要在根节点8的左子树中继续查找;
- 由于 3<6,因此在结点 3 的右子树中进行查找,最后查询成功。
2、BST的插入
二叉排序树作为一种动态树表,其特点是树的结构通常不是一次生成的,而是在查找过程中存在关键字值等于给定值的结点时再进行插入的。
插入结点的过程如下:
- 若原二叉排序树为空,则直接插入;
- 否则,若关键字 k 小于根结点值左子树;
- 若关键字 k 大于根结点值,则插入到右子树;
插入的结点一定是一个新添加且是查找失败时的查找路径上访问的最后一个结点的左孩子或右孩子。
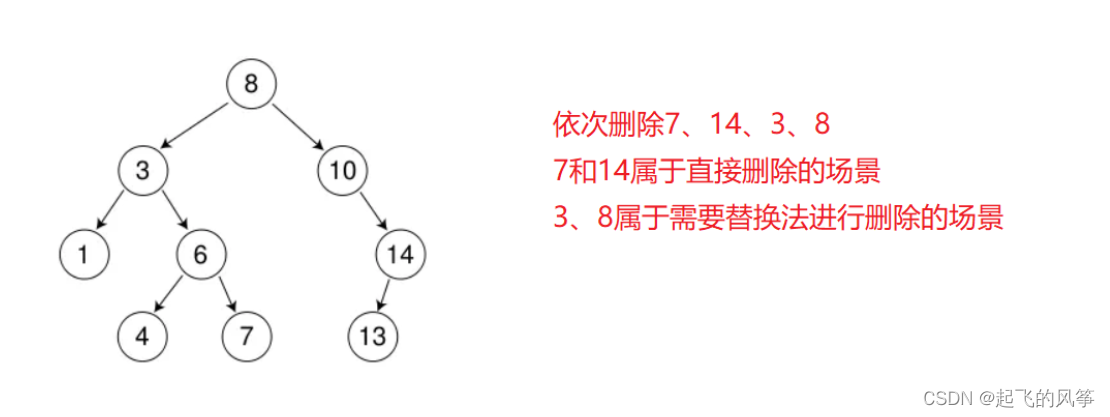
3、BST的删除
在二叉排序树中删除一个结点时,不能把以该结点为根的子树上的结点都删除,必须先删除结点从存储二叉排序树的链表上摘下,将因删除结点而断开的二叉链表重新链接起来,确保二叉排序树的性质不会丢失。
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情
况:
- a.要删除的结点无孩子结点
- b. 要删除的结点只有左孩子结点
- c. 要删除的结点只有右孩子结点
- d. 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来,因此真正的删除过程
如下
- 情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点--直接删除
- 情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点--直接删除
- 情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题--替换法删除
(三)二叉排序树的实现(非递归)
1、查找实现
代码如下:
//查找操作bool Find(const K& key){Newnode* cur = _root;while (cur){if (cur->_key < key) {cur = cur->_right;}else if (cur->_key > key) {cur = cur->left;}else {return true;}}return false;}2、插入实现
代码如下:
//插入操作bool Insert(const K& key){if (_root == nullptr){_root = new Newnode(key);return true;}Newnode* parent = nullptr;Newnode* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}//进行链接操作cur = new Newnode(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}3、删除实现
代码如下:
//删除操作bool Erase(const K& key){Newnode* parent = nullptr;Newnode* cur = _root;while (cur){//存在左右结点的情况if (cur->_key < key) {parent = cur;cur = cur->_right;}else if (cur->_key > key) {parent = cur;cur = cur->_left;}else {//不存在左if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}//不存在右else if (cur->_right == nullptr) {if (cur == _root){_root = cur->_left;}else {if (parent->_left = cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}//左右均存在else {// 找右树最小节点替代,也可以是左树最大节点替代Newnode* pminRight = cur;Newnode* minRight = cur->_right;while (minRight->_left){pminRight = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;if (pminRight->_left == minRight) {pminRight->_left = minRight->_right;}else {pminRight->_right = minRight->_right;}delete minRight;}return true;}}return false;}(四)二叉排序树的实现(递归)
递归实现都比较容易,只要大家掌握到了思想,我相信实现起来就是很容易的。
1、查找操作
//查找操作bool _FindR(Newnode* root, const K& key){if (root == nullptr)return false;if (root->_key == key)return true;if (root->_key < key)return _FindR(root->_right, key);elsereturn _FindR(root->_left, key);}2、插入操作
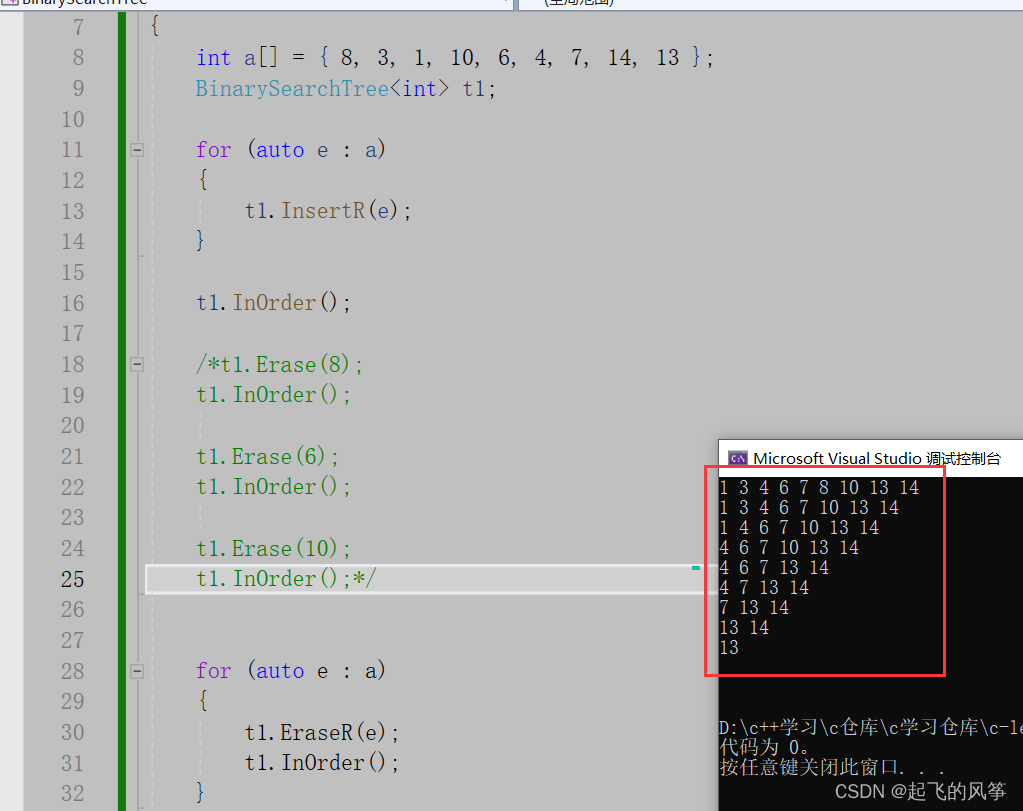
//插入操作bool _InsertR(Newnode*& root, const K& key){if (root == nullptr) {root = new Newnode(key);//root = new BSTree<K>(key);return true;}if (root->_key < key) {return _InsertR(root->_right, key);}else if (root->_key > key) {return _InsertR(root->_left, key);}else {return false;}}验证操作:

3、删除操作
//删除操作bool _EraseR(Newnode*& root,const K& key){if (root == nullptr) {root = new Newnode(key);return true;}if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Newnode* del = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{Newnode* maxleft = root->_left;while (maxleft->_left){maxleft = maxleft->_right;}swap(root->_key, maxleft->_key);return _EraseR(root->_left, key);}delete del;return true;}}验证操作:
(五)其他操作
1、析构
析构同样的使用递归来进行解决(当然也可以使用循环)。具体如下
代码实现:
//销毁操作void Destroy(Newnode*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}2、构造和拷贝构造
首先如果我想在搜索二叉树的对象进行拷贝构造能够实现吗?具体如下:

【说明】
- 我们发现是可以的,虽然我们没写;
- 这是因为拷贝构造属于默认成员函数,编译器会自动生成(注意;默认生成是属于浅拷贝)
【注意】
- 需要注意:当我们写了析构函数之后程序就会出问题;
- 因为搜索二叉树涉及资源申请,如果是浅拷贝,在析构的时候就会对一块空间析构两次
所以此时就需要写一个深拷贝的拷贝构造函数(递归版本)
Newnode* Copy(Newnode* root)
{if (root == nullptr)return nullptr;Newnode* newRoot = new Newnode(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;
}此时因为有了拷贝构造,编译器就不会生成默认的构造函数了,就需要我们自己写(C++11提供了一个关键字——default,可以强制编译器生成默认构造)
BinarySearchTree() = default; // 制定强制生成默认构造此时,它就会走初始列表用缺省值去初始化:

3、赋值重载
- 最后实现一下赋值重载的操作:
BinarySearchTree<K>& operator=(BinarySearchTree<K> t)
{swap(_root, t._root);return *this;
}代码演示:

【代码总结】
- BSTree.h:
#pragma oncetemplate<class K>struct BSTree{BSTree<K>* _left;BSTree<K>* _right;K _key;BSTree(const K& key): _left(nullptr), _right(nullptr), _key(key){}};template<class K>class BinarySearchTree{typedef BSTree<K> Newnode;public:BinarySearchTree() = default; // 制定强制生成默认构造BinarySearchTree<K>& operator=(BinarySearchTree<K> t){swap(_root, t._root);return *this;}BinarySearchTree(const BinarySearchTree<K>& t){_root = Copy(t._root);}~BinarySearchTree(){Destroy(_root);}//插入操作bool Insert(const K& key){if (_root == nullptr){_root = new Newnode(key);return true;}Newnode* parent = nullptr;Newnode* cur = _root;while (cur){if (cur->_key < key) {parent = cur;cur = cur->_right;}else if (cur->_key > key) {parent = cur;cur = cur->_left;}else {return false;}}//进行链接操作cur = new Newnode(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}//查找操作bool Find(const K& key){Newnode* cur = _root;while (cur){if (cur->_key < key) {cur = cur->_right;}else if (cur->_key > key) {cur = cur->left;}else {return true;}}return false;}//删除操作bool Erase(const K& key){Newnode* parent = nullptr;Newnode* cur = _root;while (cur){//存在左右结点的情况if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else {//不存在左if (cur->_left == nullptr) {if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}//不存在右else if (cur->_right == nullptr) {if (cur == _root){_root = cur->_left;}else {if (parent->_left = cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}//左右均存在else {// 找右树最小节点替代,也可以是左树最大节点替代Newnode* pminRight = cur;Newnode* minRight = cur->_right;while (minRight->_left){pminRight = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;if (pminRight->_left == minRight) {pminRight->_left = minRight->_right;}else {pminRight->_right = minRight->_right;}delete minRight;}return true;}}return false;}///// 递归版本bool FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key){return _InsertR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}void InOrder(){_Inorder(_root);cout << endl;}protected:Newnode* Copy(Newnode* root){if (root == nullptr)return nullptr;Newnode* newRoot = new Newnode(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}//销毁操作void Destroy(Newnode*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}//查找操作bool _FindR(Newnode* root, const K& key){if (root == nullptr)return false;if (root->_key == key)return true;if (root->_key < key)return _FindR(root->_right, key);elsereturn _FindR(root->_left, key);}//插入操作bool _InsertR(Newnode*& root, const K& key){if (root == nullptr) {root = new Newnode(key);return true;}if (root->_key < key) {return _InsertR(root->_right, key);}else if (root->_key > key) {return _InsertR(root->_left, key);}else {return false;}}//删除操作bool _EraseR(Newnode*& root, const K& key){if (root == nullptr) {root = new Newnode(key);return true;}if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Newnode* del = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{Newnode* maxleft = root->_left;while (maxleft->_left){maxleft = maxleft->_right;}swap(root->_key, maxleft->_key);return _EraseR(root->_left, key);}delete del;return true;}}//中序遍历void _Inorder(Newnode* root){if (root == nullptr) {return;}_Inorder(root->_left);cout << root->_key << " ";_Inorder(root->_right);}private:Newnode* _root = nullptr;};
(六)总结
以上便是关于二叉搜索树的模拟实现。感谢大家的观看与支持!!!

相关文章:

二叉搜索树(BST)的模拟实现
序言: 构造一棵二叉排序树的目的并不是为了排序,而是为了提高查找效率、插入和删除关键字的速度,同时二叉搜索树的这种非线性结构也有利于插入和删除的实现。 目录 (一)BST的定义 (二)二叉搜…...

【MFC】01.MFC框架-笔记
基本概念 MFC Microsoft Fundation class 微软基础类库 框架 基于Win32 SDK进行的封装 属性:缓解库关闭 属性->C/C/代码生成/运行库/MTD 属性->常规->MFC的使用:在静态库中使用MFC,默认是使用的共享DLL,运行时库 SD…...

基于ArcGIS污染物浓度及风险的时空分布
在GIS发展的早期,专业人士主要关注于数据编辑或者集中于应用工程,以及主要把精力花费在创建GIS数据库并构造地理信息和知识。慢慢的,GIS的专业人士开始在大量的GIS应用中使用这些知识信息库。用户应用功能全面的GIS工作站来编辑地理数据集&am…...

【项目开发计划制定工作经验之谈】
一、背景介绍 随着信息技术的发展,项目管理越来越受到企业和组织的重视。项目管理是一项旨在规划、组织、管理和控制项目的活动,以达到特定目标的过程。项目开发计划是项目管理的一个重要组成部分,它是指定项目目标、工作范围、进度、质量、…...

基于STM32的格力空调红外控制
基于STM32的格力空调红外控制 1.红外线简介 在光谱中波长自760nm至400um的电磁波称为红外线,它是一种不可见光。目前几乎所有的视频和音频设备都可以通过红外遥控的方式进行遥控,比如电视机、空调、影碟机等,都可以见到红外遥控的影子。这种技…...

rust中thiserror怎么使用呢?
thiserror 是一个Rust库,可以帮助你更方便地定义自己的错误类型。它提供了一个类似于 macro_rules 的宏,可以帮助你快速地定义错误类型,并为错误添加上下文信息。下面是一个使用 thiserror 的示例: 首先,在你的Rust项…...

ceph tier和bcache区别
作者:吴业亮 博客:wuyeliang.blog.csdn.net Ceph tier(SSD POOL HDD POOL)不推荐的原因: 数据在两个资源池之间迁移代价太大,存在粒度问题(对象级别),且需要进行write…...

Idea 2023.2 maven 打包时提示 waring 问题解决
Version idea 2023.2 问题 使用 Maven 打包 ,控制台输出 Waring 信息 [WARNING] [WARNING] Plugin validation issues were detected in 7 plugin(s) [WARNING] [WARNING] * org.apache.maven.plugins:maven-dependency-plugin:3.3.0 [WARNING] * org.apache.…...
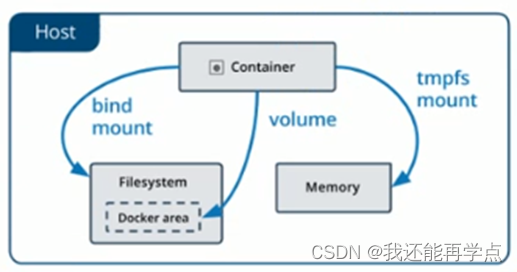
docker数据持久化
在Docker中若要想实现容器数据的持久化(所谓的数据持久化即数据不随着Container的结束而销毁),需要将数据从宿主机挂载到容器中。目前Docker提供了三种不同的方式将数据从宿主机挂载到容器中。 (1)Volumes:…...

安全防护,保障企业图文档安全的有效方法
随着企业现在数据量的不断增加和数据泄露事件的频发,图文档的安全性成为了企业必须高度关注的问题。传统的纸质文件存储方式已不适应现代企业的需求,而在线图文档管理成为了更加安全可靠的数字化解决方案。那么在在线图文档管理中,如何采取有…...

Open3D (C++) 基于拟合平面的点云地面点提取
目录 一、算法原理1、原理概述2、参考文献二、代码实现三、结果展示1、原始点云2、提取结果四、相关链接本文由CSDN点云侠原创,原文链接。爬虫网站自重,把自己当个人,爬些不完整的误导别人有意思吗???? 一、算法原理...
 - OneForAll 简单应用)
【Linux】Kali Linux 渗透安全学习笔记(2) - OneForAll 简单应用
OneForAll (以下简称“OFA”)是一个非常好用的子域收集工具,可以通过一级域名找到旗下的所有层级域名,通过递归的方式我们很容易就能够知道此域名下的所有域名层级结构,对于进一步通过域名推测站点功能起到非常重要的作…...
DAY56:单调栈(二)下一个最大元素Ⅱ(环形数组处理思路)
文章目录 思路写法1完整版环形数组处理:i取模,遍历两遍写法2完整版(环形数组推荐写法)debug测试:逻辑运算符短路特性result数组在栈口取元素,是否会覆盖原有数值? 给定一个循环数组 nums &#…...

kafka简介
kafka是什么? Kafka最初采用Scala语言开发的一个多分区、多副本并且基于ZooKeeper协调的分布式消息系统。目前Kafka已经定位为一个分布式流式处理平台,它的特性有高吞吐、可持久化、可水平扩展、支持流处理。 Apache Kafka是一个分布式的发布-订阅消息系…...
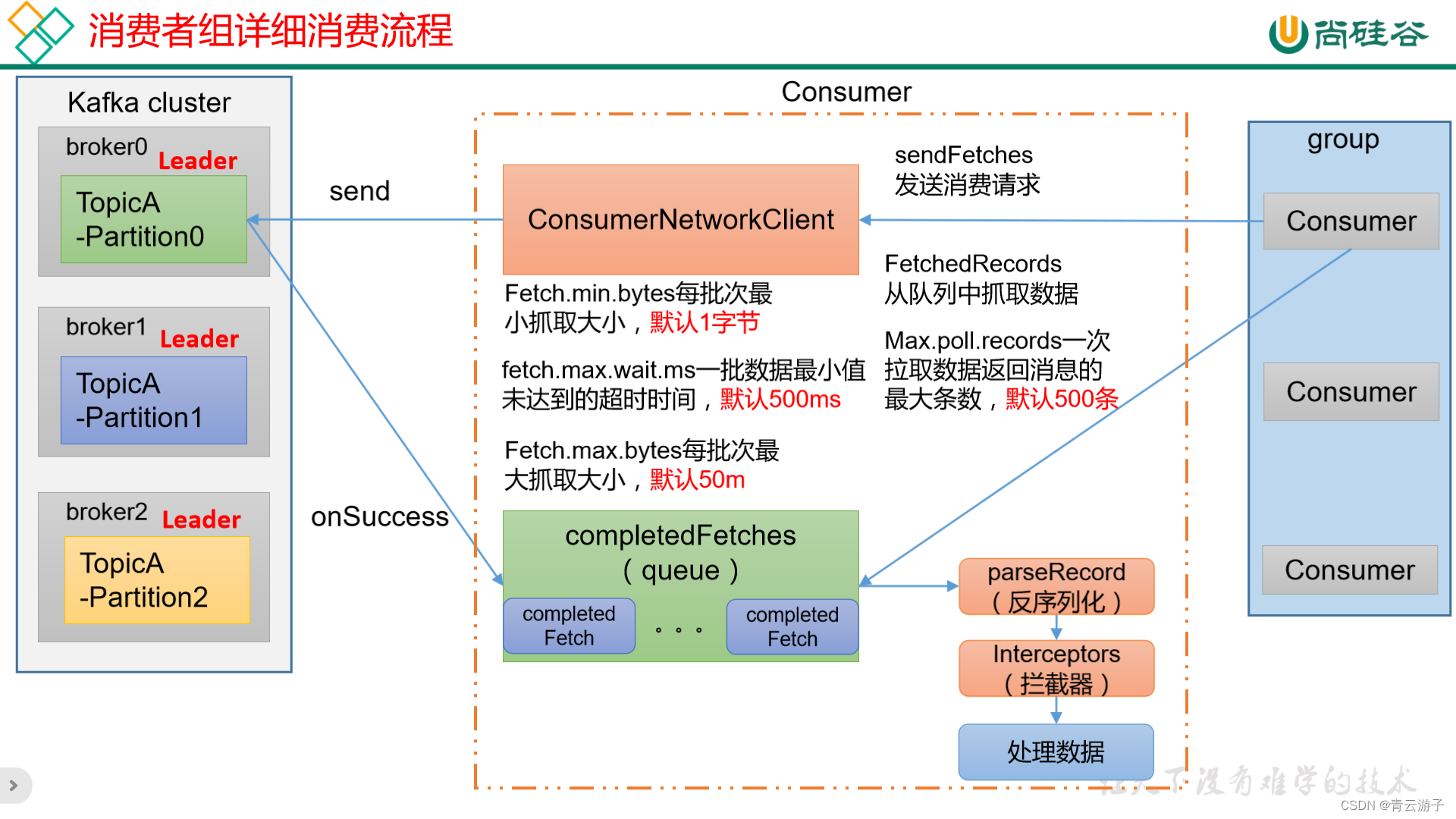
Kafka-消费者组消费流程
消费者向kafka集群发送消费请求,消费者客户端默认每次从kafka集群拉取50M数据,放到缓冲队列中,消费者从缓冲队列中每次拉取500条数据进行消费。...
FFmepg视频解码
1 前言 上一篇文章<FFmpeg下载安装及Windows开发环境设置>介绍了FFmpeg的下载安装及环境配置,本文介绍最简单的FFmpeg视频解码示例。 2 视频解码过程 本文只讨论视频解码。 FFmpeg视频解码的过程比较简单,实际就4步: 打开媒体流获取…...

SpringCloud深入理解 | 生产者、消费者
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! SpringCloud Spring Cloud是一组用于构建分布式系统和微服务架构的开源框架和工具集合。它是在Spring生态系统的基础上构建的,旨在简化开发人员构建分布式…...

web题型
0X01 命令执行 漏洞原理 没有对用户输入的内容进行一定过滤直接传给shell_exec、system一类函数执行 看一个具体例子 cmd1|cmd2:无论cmd1是否执行成功,cmd2将被执行 cmd1;cmd2:无论cmd1是否执行成功,cmd2将被执行 cmd1&cmd2:无论cmd1是否执行成…...
使用curl和postman调用Azure OpenAI Restful API
使用curl在cmd中调用时,注意:json大括号内的每一个双引号前需要加上\ curl https://xxxopenai.openai.azure.com/openai/deployments/Your_deployid/chat/completions?api-version2023-05-15 -H "Content-Type: application/json" -H "…...

草莓叶病害数据集
1.草莓数据集有两个文件夹 训练集 健康文件夹(2819张) 草莓叶焦病害(3327张) 数据集可以关注最后一行 import numpy as np import os import matplotlib.pyplot as plt import cv2import warnings warnings.filterwarnings(igno…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...
