当前位置： 首页 > news >正文

软件外包开发的后台开发语言

news 2026/4/1 14:22:55

在软件外包开发中，后台语言的选择通常取决于项目需求、客户偏好、团队技能和开发效率。今天和大家分享一些常用的后台语言及选择它们的原因，希望对大家有所帮助。北京木奇移动技术有限公司，专业的软件外包开发公司，欢迎交流合作。

 

1. Java：Java是一种面向对象的编程语言，广泛用于企业级应用。它具有优秀的性能、高度的可移植性和大量的库和框架，如Spring和Hibernate。Java也有着广泛的开发者社区和丰富的学习资源，这使得找到有经验的Java开发者相对容易。

2. Python：Python以其简洁的语法和高效的开发速度而受到许多开发者的喜爱。它有大量的库和框架，如Django和Flask，可以用于快速开发Web应用。Python也常被用于数据分析和机器学习项目。

3. PHP：PHP是一种专为Web开发设计的语言，它在Web开发中有着广泛的应用。PHP有许多成熟的框架，如Laravel和Symfony，可以帮助开发者快速构建应用。PHP也有着大量的开发者和丰富的学习资源。

4. Node.js：Node.js不是一种语言，而是一个运行JavaScript的平台。由于JavaScript在前端开发中的广泛应用，使用Node.js可以让开发者用同一种语言进行前后端开发，提高开发效率。Node.js也有许多优秀的框架，如Express.js和Koa.js。

5. C#：C#是Microsoft开发的一种面向对象的编程语言，主要用于开发Windows应用。C#也可以用于开发Web应用，特别是在使用.NET框架的情况下。如果客户的系统环境是Windows，或者项目需要与Microsoft的其他产品（如SQL Server）集成，那么C#可能是一个好的选择。

6. Ruby：Ruby是一种简洁而强大的语言，Ruby on Rails是一个流行的Web开发框架。Ruby的特点是开发速度快，语法优雅，适合快速开发和原型设计。

 

相关文章：

软件外包开发的后台开发语言

在软件外包开发中，后台语言的选择通常取决于项目需求、客户偏好、团队技能和开发效率。今天和大家分享一些常用的后台语言及选择它们的原因，希望对大家有所帮助。北京木奇移动技术有限公司，专业的软件外包开发公司，欢迎交流合作。…...

编程日记 2023/8/3 14:35:32

自动驾驶感知系统-全球卫星定位系统

卫星定位系统 车辆定位是让无人驾驶汽车获取自身确切位置的技术，在自动驾驶技术中定位担负着相当重要的职责。车辆自身定位信息获取的方式多样，涉及多种传感器类型与相关技术。自动驾驶汽车能够持续安全可靠运行的一个关键前提是车辆的定位系统必须实时…...

编程日记 2023/8/3 14:34:31

数据结构 | 基本数据结构——队列

目录 一、何谓队列 二、队列抽象数据类型 三、用Python实现队列 四、模拟：传土豆 五、模拟：打印任务 5.1 主要模拟步骤 5.2 Python实现 一、何谓队列 队列是有序集合，添加操作发生在“尾部”，移除操作则发生在“头部”。新…...

编程日记 2023/8/3 14:33:29

QT在label上透明绘图（二）

前面步骤参考前一篇文章 QT在label上透明绘图 一、给TransparentLabel类添加double transparency;变量， 二、ui添加doublespinbox，调整透明参数 void MainWindow::on_doubleSpinBox_valueChanged(double arg1) {transparentLabel->transparencyarg1;…...

编程日记 2023/8/3 14:32:28

微信小程序使用editor富文本编辑器 以及回显 全屏弹窗的模式

<!--富文本接收的位置--><view class"white-box"><view class"title"><view class"yellow-fence"></view><view class"v1">教研记录</view></view><view class"add-btn"…...

编程日记 2023/8/3 14:31:25

在CSDN学Golang场景化解决方案（基于gin框架的web开发脚手架）

一&#xff0c;中间件统一实现Oauth2身份验证 在Golang基于Gin框架开发Web应用程序时&#xff0c;可以使用gin-oauth2来实现Oauth2身份验证。下面是简单的步骤&#xff1a; 安装gin-oauth2包&#xff1a;go get github.com/appleboy/gin-oauth2导入依赖&#xff1a;import &q…...

编程日记 2023/8/3 14:30:24

关于Express 5

目录 1、概述 2、Express 5的变化 2.1 弃用或删除内容的列表&#xff1a; app.param&#xff08;name&#xff0c;fn&#xff09;名称中的前导冒号&#xff08;&#xff1a;&#xff09; app.del() app.param&#xff08;fn&#xff09; 复数方法名 res.json&#xff0…...

编程日记 2023/8/3 14:29:22

ftrace 原理详细分析

》内核新视界文章汇总《 文章目录 ftrace 原理分析1 简介2 ftrace 的编译器支持2.1 HAVE_FUNCTION_TRACER 选项对 ftrace 的支持2.2 HAVE_DYNAMIC_FTRACE 选项对动态 ftrace 的支持 3 ftrace 的初始化4 function trace 流程5 总结 ftrace 原理分析 1 简介 ftrace 是一个内核…...

编程日记 2023/8/3 14:28:21

UWB定位技术和蓝牙AOA有哪些不同？-高精度室内定位技术对比

UWB超宽带定位 UWB&#xff08;Ultra Wide Band &#xff09;即超宽带技术&#xff0c;它是一种无载波通信技术&#xff0c;利用纳秒级的非正弦波窄脉冲传输数据&#xff0c;因此其所占的频谱范围很宽。传统的定位技术是根据信号强弱来判别物体位置&#xff0c;信号强弱受外界…...

编程日记 2023/8/3 14:27:20

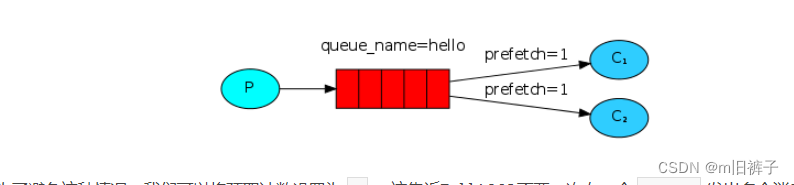
【RabbitMQ】golang客户端教程2——工作队列

任务队列/工作队列 在上一个教程中&#xff0c;我们编写程序从命名的队列发送和接收消息。在这一节中&#xff0c;我们将创建一个工作队列&#xff0c;该队列将用于在多个工人之间分配耗时的任务。 工作队列&#xff08;又称任务队列&#xff09;的主要思想是避免立即执行某些…...

编程日记 2023/8/3 14:26:18

芯旺微冲刺IPO，车规级MCU竞争白热化下的“隐忧”凸显

在汽车智能化和电动化发展带来的巨大蓝海市场下&#xff0c;产业链企业迎来了一波IPO小高潮。 日前&#xff0c;上海芯旺微电子技术股份有限公司&#xff08;以下简称“芯旺微”&#xff09;在科创板的上市申请已经被上交所受理&#xff0c;拟募资17亿元&#xff0c;用于投建车…...

编程日记 2023/8/3 14:25:16

HTML ＜s＞ 标签

例子 可以像这样标记删除线文本&#xff1a; 在 HTML 5 中&#xff0c;<s>仍然支持</s>已经不支持这个标签了。 浏览器支持 元素ChromeIEFirefoxSafariOpera<s>YesYesYesYesYes 所有浏览器都支持 <s> 标签。 定义和用法 <s> 标签可定义加…...

编程日记 2023/8/3 14:24:15

微信小程序 - scroll-view组件之上拉加载下拉刷新（解决上拉加载不触发）

前言 最近在做微信小程序项目中&#xff0c;有一个功能就是做一个商品列表分页限流然后实现上拉加载下拉刷新功能&#xff0c;遇到了一个使用scroll-viwe组件下拉刷新事件始终不触发问题&#xff0c;网上很多说给scroll-view设置一个高度啥的就可以解决&#xff0c;有些人设置了…...

编程日记 2023/8/3 14:23:14

rust usize与i64怎么比较大小？

在Rust中&#xff0c; usize 和 i64 是不同的整数类型&#xff0c;它们的位数和表示范围可能不同。因此&#xff0c;直接比较 usize 和 i64 是不允许的。如果需要比较它们的大小&#xff0c;可以将它们转换为相同的类型&#xff0c;然后进行比较。 要将 usize 转换为 i64 &…...

编程日记 2023/8/3 14:22:13

电脑更新win10黑屏解决方法

电脑更新win10黑屏解决方法 电脑黑屏出现原因解决步骤 彻底解决 电脑黑屏 出现原因 系统未更新成功就关机&#xff0c;导致系统出故障无法关机 解决步骤 首先长安电源键10s关机 按电源键开机&#xff0c;出现logo时按F8进入安全模式。 进入自动修复环境后&#xff0c;单击…...

编程日记 2023/8/3 14:21:11

STM32入门——外部中断

中断系统概述 中断&#xff1a;在主程序运行过程中&#xff0c;出现了特定的中断触发条件&#xff08;中断源&#xff09;&#xff0c;使得CPU暂停当前正在运行的程序&#xff0c;转而去处理中断程序&#xff0c;处理完成后又返回原来被暂停的位置继续运行中断优先级&#xff…...

编程日记 2023/8/3 14:20:10

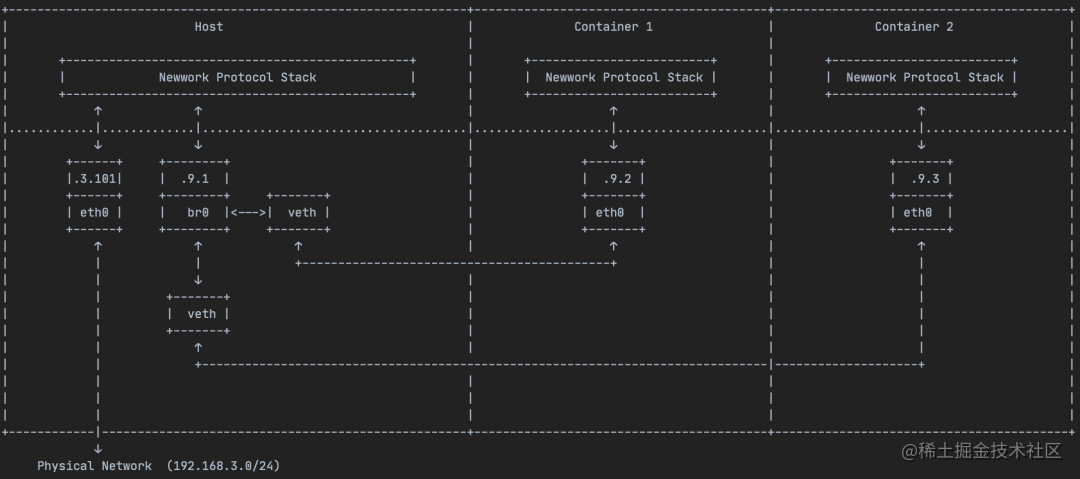
【计算机网络】NAT及Bridge介绍

OSI七层模型 七层模型介绍及举例 为通过网络将人类可读信息通过网络从一台设备传输到另一台设备&#xff0c;必须在发送设备沿 OSI 模型的七层结构向下传输数据&#xff0c;然后在接收端沿七层结构向上传输数据。 数据在 OSI 模型中如何流动 库珀先生想给帕尔梅女士发一封电…...

编程日记 2023/8/3 14:19:09

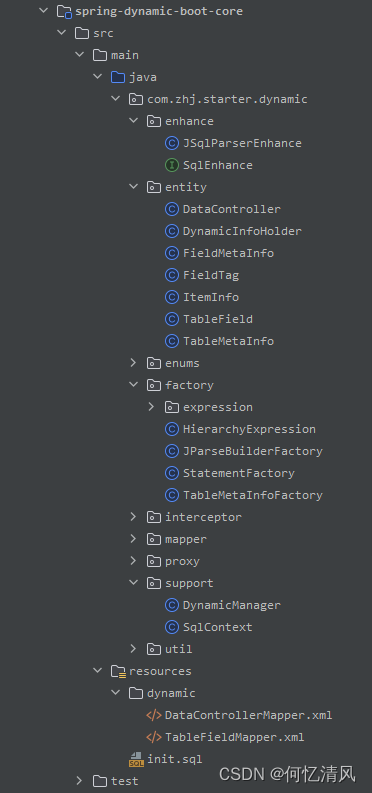
封装动态SQL的插件

最近根据公司的业务需要封装了一个简单的动态SQL的插件&#xff0c;要求是允许用户在页面添加SQL的where条件&#xff0c;然后开发者只需要给某个接口写查询对应的表&#xff0c;参数全部由插件进行拼接完成。下面是最终实现&#xff1a; 开发人员只需要在接口写上下面的查询SQ…...

编程日记 2023/8/3 14:18:05

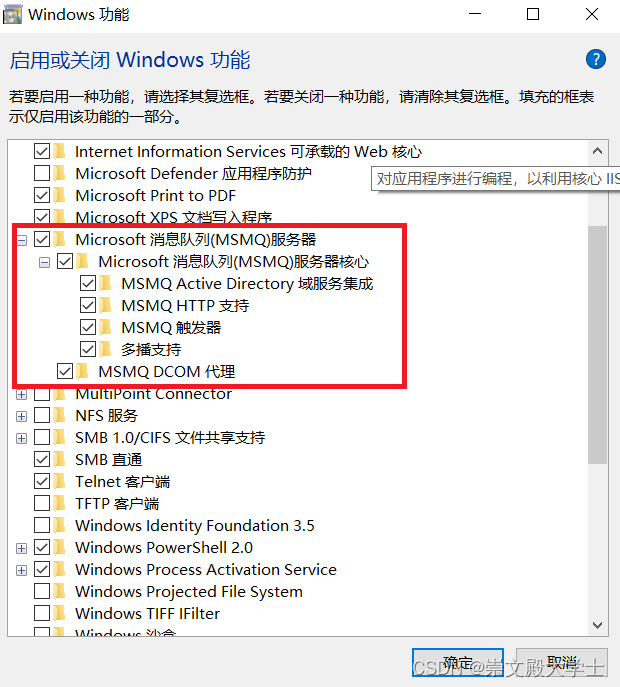
C# Microsoft消息队列服务器的使用 MSMQ

先安装消息队列服务器 private static readonly string path ".\\Private$\\myQueue";private void Create(){if (!MessageQueue.Exists(path)){MessageQueue.Create(path);}}private void Send(){Stopwatch stopwatch new Stopwatch();stopwatch.Start();Message…...

编程日记 2023/8/3 14:17:03

Kafka3.0.0版本——生产者如何提高吞吐量

目录 一、生产者提高吞吐量参数设置二、产者提高吞吐量代码示例 一、生产者提高吞吐量参数设置 batch.size&#xff1a;设置批次大小&#xff0c;默认16klinger.ms&#xff1a;设置等待时间&#xff0c;修改为5-100msbuffer.memory&#xff1a;设置缓冲区大小&#xff0c; 默认…...

编程日记 2023/8/3 14:16:02

打破设备壁垒：Sunshine让游戏自由流动的串流革命

打破设备壁垒&#xff1a;Sunshine让游戏自由流动的串流革命 【免费下载链接】Sunshine Self-hosted game stream host for Moonlight. 项目地址: https://gitcode.com/GitHub_Trending/su/Sunshine 想象一下&#xff1a;你在客厅的高性能电脑上开始了一场紧张刺激的3A大…...

编程新知 2026/4/1 11:45:45

宝可梦随机化终极指南：Universal Pokemon Randomizer ZX 完全使用教程

宝可梦随机化终极指南&#xff1a;Universal Pokemon Randomizer ZX 完全使用教程 【免费下载链接】universal-pokemon-randomizer-zx Public repository of source code for the Universal Pokemon Randomizer ZX 项目地址: https://gitcode.com/gh_mirrors/un/universal-po…...

编程新知 2026/4/1 11:35:41

电容耦合等离子刻蚀（CCP）在先进芯片制造中的关键作用与工艺优化

1. 电容耦合等离子刻蚀&#xff08;CCP&#xff09;技术解析 第一次接触CCP刻蚀设备时&#xff0c;我被它那看似简单却暗藏玄机的结构震撼到了——两块金属电极板&#xff0c;加上射频电源&#xff0c;就能实现纳米级的精密加工。这种利用电容耦合原理产生等离子体的技术&#…...

编程新知 2026/4/1 11:07:28

Kandinsky-5.0-I2V-Lite-5s后端集成：Node.js环境下的高性能API服务构建

Kandinsky-5.0-I2V-Lite-5s后端集成&#xff1a;Node.js环境下的高性能API服务构建 1. 引言 想象一下&#xff0c;你正在开发一个创意设计平台&#xff0c;用户上传一张图片&#xff0c;几秒钟后就能看到它变成了一段生动的视频。这种从静态图像到动态视频的转换能力&#xf…...

编程新知 2026/4/1 10:49:10

使用Python轻松管理Word页脚

在日常的办公自动化中&#xff0c;处理Word文档是许多人绕不开的环节。无论是生成报告、合同&#xff0c;还是制作项目文档&#xff0c;Word都是一个不可或缺的工具。然而&#xff0c;当文档数量庞大&#xff0c;或者需要频繁更新时&#xff0c;那些看似简单的重复性任务&#…...

编程新知 2026/4/1 8:42:56

信创协同办公价格与成本：这样选，性价比直接拉满！

“一套信创协同办公到底多少钱&#xff1f;”“是按人头收费&#xff0c;还是按项目打包算&#xff1f;”“前期买着便宜&#xff0c;后期维护会不会无底洞&#xff1f;”不管是政企单位采购&#xff0c;还是企业选型&#xff0c;这三个问题几乎是所有人的核心顾虑。毕竟信创办…...

编程新知 2026/4/1 7:51:49

Phi-3-mini-128k-instruct实战：利用VLOOKUP逻辑进行多源数据关联与报告生成

Phi-3-mini-128k-instruct实战&#xff1a;利用VLOOKUP逻辑进行多源数据关联与报告生成 1. 引言 如果你用过Excel&#xff0c;肯定对VLOOKUP这个函数不陌生。它的核心就一句话&#xff1a;根据一个表格里的某个值&#xff0c;去另一个表格里找到对应的信息&#xff0c;然后“…...

编程新知 2026/4/1 7:23:05

别再只用官方节点了！手把手教你安装n8n社区节点，解锁隐藏工作流能力

解锁n8n隐藏潜能&#xff1a;社区节点深度应用指南 你是否曾在n8n中构建工作流时&#xff0c;发现官方节点无法满足某些特定需求&#xff1f;比如需要更复杂的文本处理、社交媒体深度集成&#xff0c;或是与某些小众API对接&#xff1f;这正是社区节点大显身手的时刻。作为n8n生…...

编程新知 2026/4/1 7:14:51

Chandra AI在教育领域的应用：智能学习助手开发

Chandra AI在教育领域的应用&#xff1a;智能学习助手开发 1. 引言 想象一下这样的场景&#xff1a;一个学生在深夜复习功课&#xff0c;遇到一道数学难题却找不到老师请教&#xff1b;一个上班族想学习新技能&#xff0c;但时间碎片化难以系统学习&#xff1b;一个老师面对几…...

编程新知 2026/4/1 5:47:08

R包版本冲突别头疼：手把手教你降级igraph 2.1.1，解决monocle3的orderCells报错

R包版本冲突实战指南&#xff1a;精准降级igraph解决monocle3依赖问题 当你满怀期待地安装好monocle3准备进行单细胞拟时序分析时&#xff0c;突然弹出的nei() was deprecated in igraph 2.1.0报错就像一盆冷水浇灭了热情。这种R包版本冲突在生物信息学分析中屡见不鲜&#xff…...

编程新知 2026/4/1 5:45:05