动态规划之树形DP
动态规划之树形DP
- 树形DP
- 何为树形DP
- 树形DP例题
- HDU-1520 Anniversary party
- HDU-2196 Computer
- 834. 树中距离之和
树形DP
何为树形DP
树形DP是指在“树”这种数据结构上进行的动态规划:给出一颗树,要求以最少的代价(或取得最大收益)完成给定的操作。通常这类问题规模比较大,枚举算法效率低,无法胜任,贪心算法不能求得最优解,因此需要用动态规划进行求解。
在树上做动态规划显得非常合适,因为树本身有“子结构”性质(树和子树),具有递归性,符合DP性质。相比线性DP,树形DP的状态转移方程更加直观。
树形动态规划(Tree DP)是一种动态规划算法,在处理树状结构(例如树、森林、有向无环图等)上的问题时非常常见和有效。树形动态规划通过将问题拆解为子问题,并利用子问题的解来求解更大规模的问题。
在树形动态规划中,我们需要定义一个适合的状态和状态转移方程。一般来说,状态可以定义为以当前节点为根的子树的某种性质,例如最大路径和、最长路径长度、最大权值和等等。而状态转移方程则描述了如何由子节点的状态计算当前节点的状态。
树形动态规划的典型做法是使用深度优先搜索(DFS)遍历整个树,在遍历过程中进行状态的计算和更新。通过递归地计算子节点的状态,并将其传递给父节点,可以得到整个树的最终状态。
在实现树形动态规划时,需要注意避免重复计算,可以使用记忆化搜索或者自底向上的方式进行计算。此外,还要注意选择合适的遍历顺序,以保证子问题的状态在计算当前节点状态时已经求解完毕。
总而言之,树形动态规划是一种针对树状结构问题的动态规划算法,通过拆解问题为子问题,并利用子问题的解求解更大规模的问题。它在解决树相关的问题时具有重要的应用价值。
树形DP例题
HDU-1520 Anniversary party
HDU-1520 Anniversary party
题目大意:
邀请员工参加party,但是为了避免员工和直属上司发生尴尬,规定员工和直属上司不能同时出席。
也就是每个人代表树中一个结点,每个结点拥有一个权值,相邻的父结点和子结点只能选择一个,问如何取才能使总权值之和最大。
员工编号从1到N。第一行输入包含数字N。1 < = N < = 6000。随后的N行中的每一行都包含相应员工的愉快度评级。欢乐评级是一个介于-128到127之间的整数。然后是描述主管关系树的T行。树规范的每一行都具有以下形式: L K 这意味着第K个员工是第L个员工的直接主管。输入以一行结束 0 0
解题思路:
根据DP的解题思路,定义状态为:
d p [ i ] [ 0 ] dp[i][0] dp[i][0],表示不选择当前结点时候的最优解
d p [ i ] [ 1 ] dp[i][1] dp[i][1],表示选择当前结点时候的最优解
其中状态转移方程分为下面两种情况:
- 不选择当前结点,则子结点可选可不选,取其中的最大值即可,也就是 d p [ u ] [ 0 ] + = m a x ( d p [ s o n ] [ 0 ] , d p [ s o n ] [ 1 ] ) dp[u][0] += max(dp[son][0], dp[son][1]) dp[u][0]+=max(dp[son][0],dp[son][1])
- 选择当前结点,则其子结点不能选, d p [ u ] [ 1 ] + = d p [ s o n ] [ 0 ] dp[u][1] += dp[son][0] dp[u][1]+=dp[son][0]
AC代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 6010;
vector<int>tree[maxn];
int dp[maxn][2], father[maxn], value[maxn];
void dfs(int u) {dp[u][0] = 0; // 不参加partydp[u][1] = value[u]; // 参加partyfor(int i = 0; i < tree[u].size(); i++) {int son = tree[u][i];dfs(son); // 深搜子结点dp[u][0] += max(dp[son][0], dp[son][1]); // 父结点不选,子结点可选可不选dp[u][1] += dp[son][0]; // 父结点选择,子结点不能选}
}
int main() {int n, a, b;while(~scanf("%d", &n)) {for(int i = 1; i <= n; i++) {scanf("%d", &value[i]);tree[i].clear();father[i] = -1;}memset(dp, 0, sizeof(dp));while(true) { // 建树scanf("%d%d", &a, &b);if(a == 0 && b == 0) break;tree[b].push_back(a);father[a] = b; // 父子关系,表示a的父亲是b}for(int i = 1; i <= n; i++) {if(father[i] == -1) { // 寻找父结点,从父结点开始深搜dfs(i);printf("%d\n", max(dp[i][0], dp[i][1]));break;}}}return 0;
}
HDU-2196 Computer
HDU-2196 Computer

题目大意:
一颗树,根节点的编号是1,对其中的任意一个结点,求离这个结点最远结点的距离。
输入包含多个测试用例,每个用例的第一行是一个自然数N,N不超过10000,接下来N-1行,每行输入两个整数:第一个整数为某结点id,第二个整数为连接到这个结点需要的距离。
输出N行,表示距离第i个结点的最远距离
解题思路:
对于求解距离某结点的最长距离,应当分为两种情况:
对于任意一个结点
-
结点 i i i 的子树中的结点距离结点 i i i 的最长距离,而为了方便第二种情况的计算,第一次深搜的时候需要记录结点 i i i 的子树中某个结点到该结点的最长距离和第二长的距离。
-
第二种情况就是结点 i i i 往上走,而此时往上走又分为两种情况:
从结点 i i i 往上继续走,没有走结点 i i i 的父结点到其子树的最长距离的路径
若结点 i i i 沿着其父结点的最长路径上走时,则需考虑结点 i i i 是否在其父结点的最长子树上,此时则需要用到最初求得各个结点到其它结点的最长距离和次长距离,如果结点 i i i 在其父结点的最长子树上那么 X = two + dist(i, i 的父结点),否则 X = one + dist(i, i 的父结点)
综上所述,第一种情况和第二种情况求得两个值的最大值即为答案
状态的设计:结点 i i i 的子树到 i i i 的最长距离 d p [ i ] [ 0 ] dp[i][0] dp[i][0] 以及次长距离 d p [ i ] [ 1 ] dp[i][1] dp[i][1],从结点 i i i 往上走的最长距离 d p [ i ] [ 2 ] dp[i][2] dp[i][2]
#include<bits/stdc++.h>
using namespace std;
struct Node {int id; // 子树结点编号int cost;
};
const int maxn = 10010;
int dp[maxn][3], n;
vector <Node> tree[maxn];
void init() { // 初始化和建树for(int i = 1; i <= n; i++) tree[i].clear();memset(dp, 0, sizeof(dp));int x, y;for(int i = 2; i <= n; i++) {scanf("%d%d", &x, &y);Node tmp;tmp.id = i;tmp.cost = y;tree[x].push_back(tmp);}
}
void dfs1(int father) { // 搜索以结点father为起点到子树的最长距离和次长距离int one = 0, two = 0; // one 记录father往下走的最长距离,two记录次长距离for(int i = 0; i < tree[father].size(); i++) { // 先处理子结点再处理父结点Node child = tree[father][i];dfs1(child.id); // 递归子结点,直到最底层int temp = child.cost + dp[child.id][0];if(temp >= one) {two = one;one = temp;}if(temp < one && temp > two) two = temp;}dp[father][0] = one; // 得到以father为起点的子树的最长距离dp[father][1] = two; // 得到以father为起点的子树的次长距离
}
void dfs2(int father) { // 先处理父结点再处理子结点for(int i = 0; i < tree[father].size(); i++) {Node child = tree[father][i];if(child.cost + dp[child.id][0] == dp[father][0]) // child在最长距离的子树上dp[child.id][2] = max(dp[father][1], dp[father][2]) + child.cost;else dp[child.id][2] = max(dp[father][0], dp[father][2]) + child.cost; //否则dfs2(child.id);}
}
int main() {while(~scanf("%d", &n)) {init();dfs1(1);dp[1][2] = 0;dfs2(1);for(int i = 1; i <= n; i++) {printf("%d\n", max(dp[i][0], dp[i][2]));}}return 0;
}
834. 树中距离之和
834. 树中距离之和
给定一个无向、连通的树。树中有 n 个标记为 0...n-1 的节点以及 n-1 条边 。
给定整数 n 和数组 edges , edges[i] = [ai, bi]表示树中的节点 ai 和 bi 之间有一条边。
返回长度为 n 的数组 answer ,其中 answer[i] 是树中第 i 个节点与所有其他节点之间的距离之和。
示例 1:
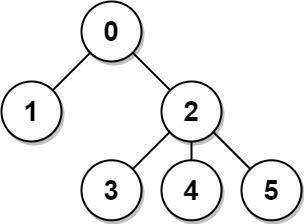
输入: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
输出: [8,12,6,10,10,10]
解释: 树如图所示。
我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
也就是 1 + 1 + 2 + 2 + 2 = 8。 因此,answer[0] = 8,以此类推。
参考灵神的题解写出来的,不得不说灵神 yyds,比官方给出的题解简单多了。
灵神的题解地址:传送门
灵神给出的解题思路如下图所示:
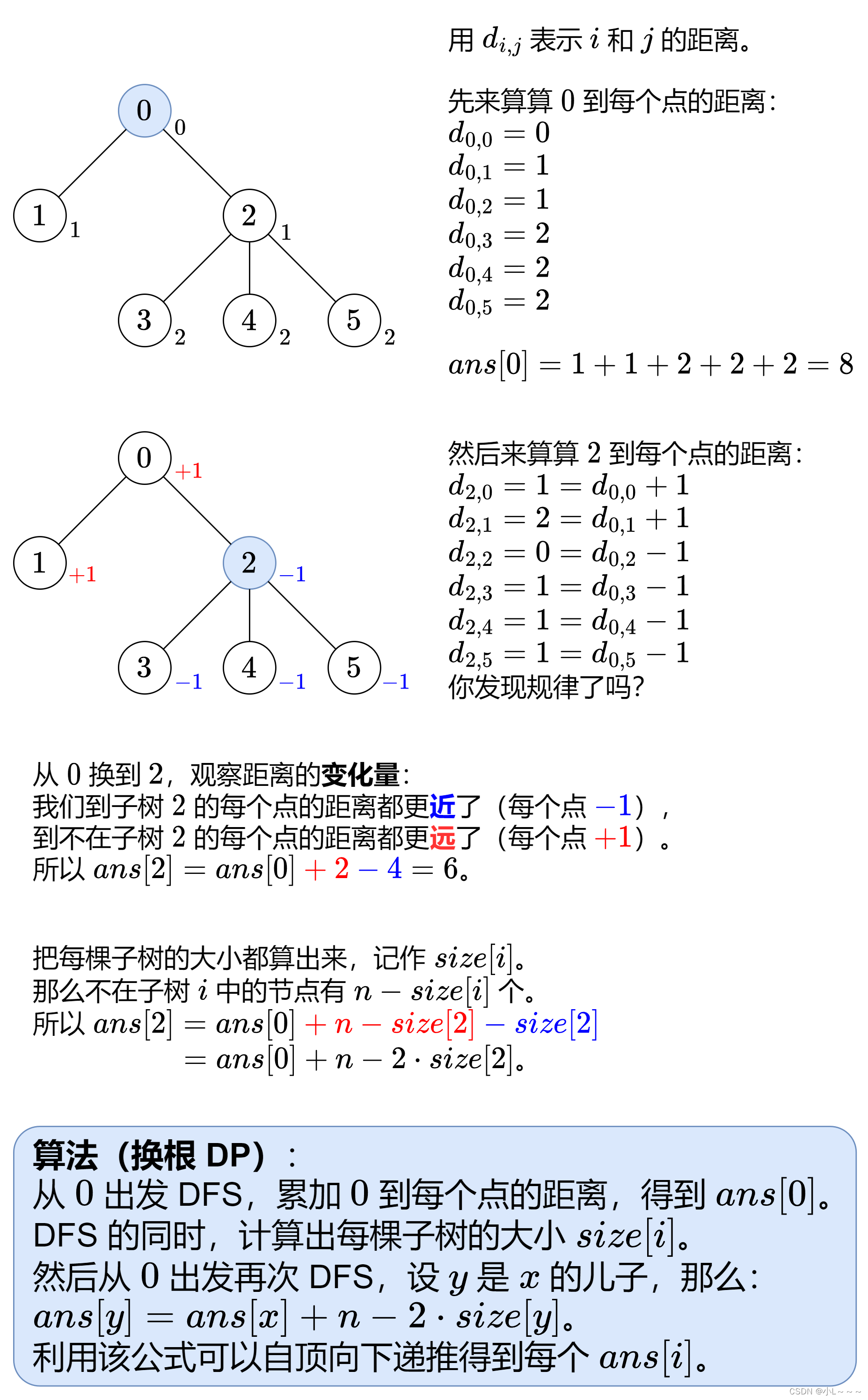
AC代码:
class Solution {
public:static const int maxn = 3e4 + 10;vector<int>tree[maxn];vector<int> sumOfDistancesInTree(int n, vector<vector<int>>& edges) {for(auto edge : edges) {tree[edge[0]].push_back(edge[1]);tree[edge[1]].push_back(edge[0]);}vector<int>ans(n);vector<int>children(n, 1); // 每颗子树所包含结点数量function<void(int, int, int)> dfs1 = [&](int child, int father, int depth) {ans[0] += depth;for(auto i : tree[child]) {if(i != father) { // 避免访问父结点dfs1(i, child, depth + 1);children[child] += children[i]; // 累加子树大小}}};dfs1(0, -1, 0); // 0 没有父结点function<void(int, int)> dfs = [&](int child, int father) {for(auto i : tree[child]) {if(i != father) {ans[i] += (ans[child] + n - children[i] * 2);dfs(i, child);}}};dfs(0, -1);return ans;}
};
相关文章:

动态规划之树形DP
动态规划之树形DP 树形DP何为树形DP 树形DP例题HDU-1520 Anniversary partyHDU-2196 Computer834. 树中距离之和 树形DP 何为树形DP 树形DP是指在“树”这种数据结构上进行的动态规划:给出一颗树,要求以最少的代价(或取得最大收益ÿ…...

嵌入式_GD32使用宏开关进行Debug串口打印调试
嵌入式_GD32使用宏开关进行Debug串口打印调试 串口Debug是一种将数据通过串口发送的方法。通过使用printf函数,我们可以将需要发送的数据格式化为字符串,并通过串口发送出去。在C语言中,通常使用串口发送数据的函数为printf函数,…...

使用 GitHub Copilot 进行 Prompt Engineering 的初学者指南(译)
文章目录 什么是 GitHub Copilot ?GitHub Copilot 可以自己编码吗?GitHub Copilot 的底层是如何工作的?什么是 prompt engineering?这是 prompt engineering 的另一个例子 使用 GitHub Copilot 进行 prompt engineering 的最佳实践提供高级上下文&…...

c++开发模式,享元模式
享元模式,个人理解,就是应用共享技术来减少类的对象创建,节省计算机资源消耗,而且能够减少维护成本 #include <iostream> #include <string> #include <vector>using namespace std;class Flyweight { public:…...
LLM大模型——langchain相关知识总结
目录 一、简介LangChain的主要价值支柱简单安装 二、 LangChain的主要模块1.Model I/Oprompt模版定义调用语言模型 2. 数据连接3. chains4. Agents5. MemoryCallbacks 三、其他记录多进程调用 主要参考以下开源文档 文档地址:https://python.langchain.com/en/lates…...

【Python】数据可视化利器PyCharts在测试工作中的应用
目录 PyCharts 简介 PyCharts 的安装 缺陷统计 测试用例执行情况 使用JavaScript情况 缺陷趋势分析 将两张图放在一个组合里(grid) 将两张图重叠成一张图(overlap) 将多张图组合在一个page 中(page࿰…...
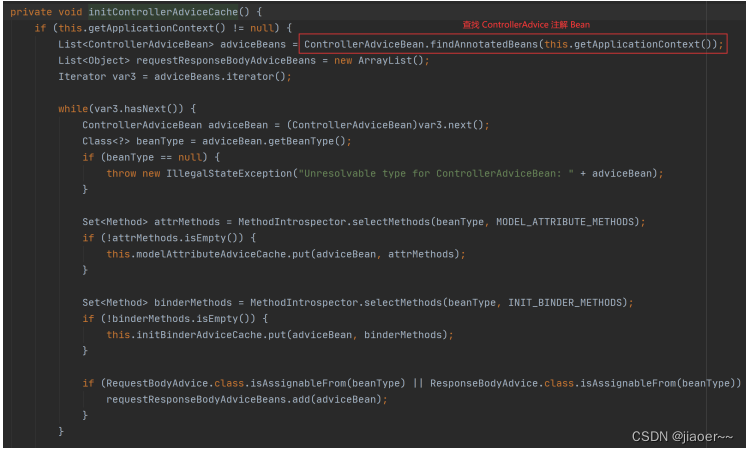
AOP的实战(统一功能处理模块)
一、用户登录权限效验 用户登录权限的发展从之前每个方法中自己验证用户登录权限,到现在统一的用户登录验证处理,它是一个逐渐完善和逐渐优化的过程。 1.1 最初用户登录验证 我们先来回顾一下最初用户登录验证的实现方法: RestController…...

时间复杂度为O(n2)的三种简单排序算法
1.冒泡排序 冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少少一个元素移动到它应该在的位置,重复n次,就完成了n个数据的排序工作。 /*** …...

LeetCode 热题 100 JavaScript --226. 翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 示例 3: 输入:root [] 输出:[] 提示: 树中节点数目范围在 [0, 100] 内 -100 < Node.val < 100 var invertTree function(root…...

hive所有窗口函数详情总结
hive窗口函数详情总结 解释语法hive开窗函数排序开窗函数样例数据RANK()DENSE_RANK()ROW_NUMBER() 分析开窗函数样例数据:last_valuefirst_valuelaglead 其他窗口函数cume_distpercent_rank 解释 开窗函数用于为行定义一个窗口(指运算将要操作的行的集合…...

Talk | 新加坡国立大学博士生施宇钧:DragDiffusion-基于扩散模型的关键点拖拽图片编辑
本期为TechBeat人工智能社区第518期线上Talk! 北京时间8月2日(周三)20:00, 新加坡国立大学博士生—施宇钧的Talk已准时在TechBeat人工智能社区开播! 他与大家分享的主题是: “DragDiffusion-基于扩散模型的关键点拖拽图片编辑”,他…...

22 | 贝叶斯分类算法
文章目录 介绍什么是贝叶斯分类算法?贝叶斯分类算法的应用场景贝叶斯定理贝叶斯定理的基本原理贝叶斯定理的公式推导贝叶斯定理的应用举例代码介绍 什么是贝叶斯分类算法? 贝叶斯分类算法是一类基于贝叶斯定理的分类技术。在统计分类任务中,这些算法使用特定的假设来建立特…...

java.sql.SQLSyntaxErrorException: ORA-00909: 参数个数无效
问题: 在Select里采用Contact(%,#name,%)报错参数个数无效 原因: 回想以前用Mysql的时候就是这样用的,没有问题,在这里就出问题了,所以确定问题在oracle数据库上,经过查询得知,oracle和mysql…...

数据结构8-哈希表
数据结构8-哈希表 动态分配内存方式: #include <stdio.h> #include <stdlib.h>#define SIZE 20struct DataItem {int data; int key; };struct DataItem* hashArray[SIZE]; struct DataItem* dummyItem; struct DataItem* item;//获取键值 int has…...

vue3引用Font-Awesome字体图标库
环境:vue3tsviteelement plus 介绍:这里安装引用的是Font-Awesome 6.x 版本,有专业版(付费),这里只介绍免费版字体使用方法 一、安装 1.使用npm安装,终端打开项目目录或者命令行cd到目录文件夹…...

Python: Django 服务部署可能遇到的一些问题
502 bad gateway 不要用 python3 manage.py runserver 启动服务, 而要用: daphne -b 0.0.0.0 -p <端口> <工程名>.asgi:application此外,在 setting.py 中,修改: import osSECRET_KEY os.environ.get(D…...

Python爬虫时遇到连接超时解决方案
在进行Python爬虫任务时,经常会遇到连接超时(TimeoutError)错误。连接超时意味着爬虫无法在规定的时间内建立与目标服务器的连接,导致请求失败。为了帮助您解决这个常见的问题,本文将提供一些解决办法,并提…...
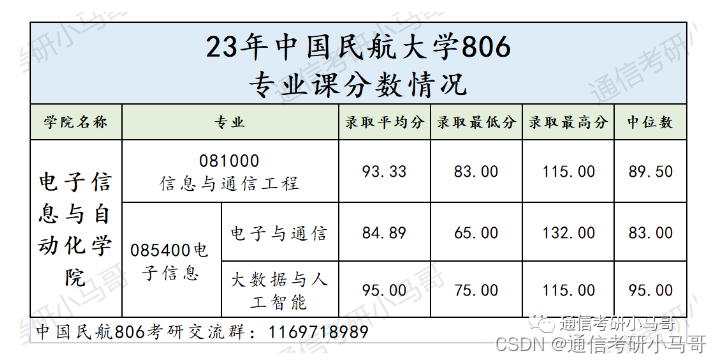
这所国字头双一流,根本招不满,学硕都没人报!
一、学校及专业介绍 中国民航大学,位于天津市,是民航局、天津市、教育部共建高校,是天津市“双一流”建设高校和高水平特色大学建设高校。 1.1 招生情况 2023年中国民航大学电子信息与自动化学院,初试考806信号与系统的一共有两…...

macos 查询端口占用 命令
在 macOS 上查询端口占用的命令是通过使用lsof(list open files)工具来实现的。 lsof可以显示当前系统中打开的文件(包括网络连接和端口)的相关信息。 打开终端应用程序(Terminal),然后输入以下…...

无代码开发:打破传统开发模式,引领数字化转型新方向
随着数字化转型的加速,企业对于高效、便捷的软件开发需求愈发旺盛。无代码开发作为一种新兴的软件开发模式,以其可视化、模块化的开发方式,为数字化转型提供了新的方向。本文将从无代码开发的优势、应用场景、如何实现等方面进行详细解读&…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
