数据结构——绪论
一、绪论
(一)基本概念
数据:数据是对客观事物的符号表示,在计算机科学中是指所有能输入到计算机中并被计算机程序处理的符号的总称。
数据元素:数据元素是数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理。一个数据元素可由若干个数据项组成,数据项是构成数据元素的不可分割的最小单位。
数据对象:数据对象是性质相同的数据元素的集合,是数据的一个子集。
数据结构:数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
数据元素都不是孤立存在的,而是在它们之间存在着某种关系,这种数据元素相互之间的关系称为结构。
数据结构三要素:
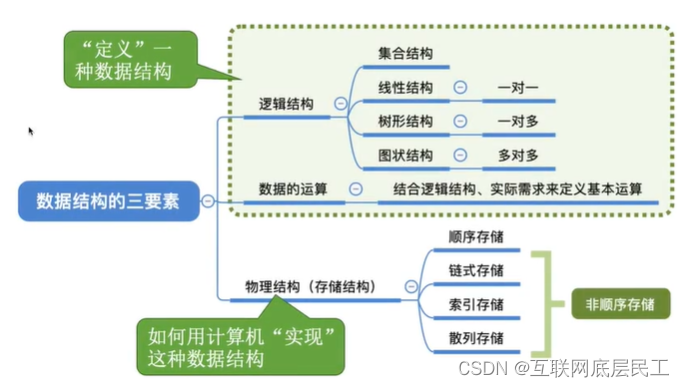
1、逻辑结构
结构定义中的“关系”描述的是数据元素之间的逻辑关系,因此又称为数据的逻辑结构
根据数据元素之间关系的不同特性,通常有下列4类基本结构:
-
集合:结构中的数据元素之间除了“同属于一个集合”的关系外,别无其他关系。
-
线性结构:结构中的数据元素之间存在一个对一个的关系。除了第一个元素,所有元素都有唯一的前驱;除了最后一个元素,所有元素都有唯一后继。
-
树形结构:结构中的数据元素之间存在一个对多个的关系
-
图状结构或网状结构:结构中的数据元素之间存在多个对多个的关系
2、数据的运算
针对于某种逻辑结构,结合实际需求,定义基本运算。
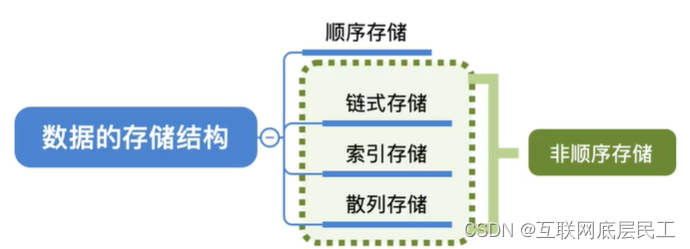
3、物理结构(存储结构)
数据结构在计算机中的表示称为数据的物理结构,又称为存储结构。
数据元素之间的关系在计算机中有两种不同的表达式:顺序映射和非顺序映射,并由此得到两种不同的存储结构:顺序存储结构和链式存储结构。
顺序映射:特点是接触元素在存储器中的相对位置来表示数据元素之间的逻辑关系。
非顺序映射:特点是借助指示元素存储地址的指针表示数据元素之间的逻辑关系。
(1)顺序存储
把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中,元素之间的关系由存储单元的邻接关系来体现。
(2)链式存储
逻辑上相邻的元素在物理位置上可以不相邻,借助指示元素存储地址的指针来表示元素之间的逻辑关系。
(3)索引存储
在存储元素信息的同时,还建立附加的索引表。索引表中的每项称为索引项,索引项的一般形式是(关键字,地址)
(4)散列存储
根据元素的关键字直接计算出该元素的存储地址,又称哈希(Hash)存储。
4、总结
(1)若采用顺序存储,则各个数据元素在物理上必须是连续的;若采用非顺序存储,则各个数据元素在物理上可以是离散的。
(2)数据的存储结构会影响存储空间分配的方便程度
(3)数据的存储结构会影响对数据运算的速度
运算的定义是针对逻辑结构的,指出运算的功能;
运算的实现是针对存储结构的,指出运算的具体操作步骤。
数据类型和抽象数据类型
数据类型
数据类型是一个值的集合和定义在此集合上的一组操作的总称。
-
原子类型。其值不可再分的数据类型。
-
结构类型。其值是由若干个成分按某种结构组成的,因此是可以再分解的,并且它的成分可以是非结构的也可以是结构的。
抽象数据类型(Abstract Data Type,ADT)
抽象数据组织及与之相关的操作。
抽象数据类型的定义由一个值域和定义在该值域上的一组操作组成。若按照其值的不同特性可以分为3种:
-
原子类型:原子类型的变量的值是不可分解的。这类抽象数据类型较少,因为一般情况下,已有的固有数据类型足以满足需求。
-
固定聚合类型:该类型的变量,其值由确定数目的成分按某种结构组成。
-
可变聚合类型:和固定聚合类型相比较,构成可变聚合类型“值”的成分的数目不确定。
显然,后两种类型可统称为结构类型。
(二)算法和算法分析

1、算法
算法是对特定问题求解步骤的一种描述,它是指令的有限序列,其中每一条指令表示一个或多个操作。一个算法还具有下列5个重要特性:
(1)有穷性:一个算法必须总是(对任何合法的输入值)在执行有穷步之后结束,且每一步都可在又穷时间内完成。
(2)确定性:算法中每一条指令必须有确切的含义,读者理解时不会产生二义性。并且在任何条件下,算法只有唯一的一条执行路径,即对于相同的输入只能得出相同的输出。
(3)可行性:一个算法是能行的,即算法中描述的操作都是可以通过已经实现的基本运算执行有限次来实现的。
(4)输入:一个算法有零个或多个的输入,这些输入取自于某个特定的对象的集合。
(5)输出:一个算法有一个或多个的输出,这些输出是同输入有着某些特定关系的量。
2、算法设计要求
通常设计一个“好”的算法应考虑达到以下目标:
(1)正确性:算法应当满足具体问题的需求。
(2)可读性:算法应具有良好的可读性,以帮助人们理解。
(3)健壮性:输入非法数据时,算法能适当地做出反应或进行处理,而不会产生莫名其妙的输出结果。
(4)效率与低存储量需求:效率指的是算法执行的时间。存储量需求值算法执行过程中所需要的最大存储空间。
3、算法效率的度量
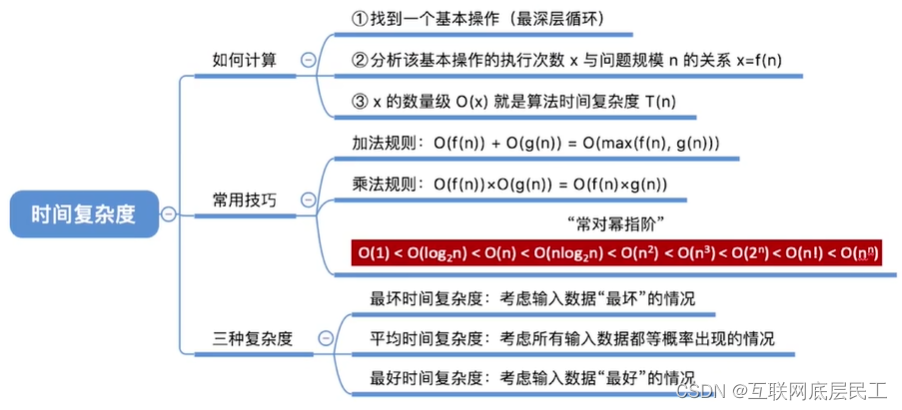
算法执行时间需通过依据该算法编制的程序在计算机上运行时所消耗的时间来度量。而度量一个程序的执行时间通常有两种方法:
(1)事后统计的方法
(2)事前分析估算的方法
一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数f(n),算法的时间度量记作:
它表示随问题规模n的增大,算法执行时间的增长率和f(n) 的增长率相同,称做算法的渐近时间复杂度,简称时间复杂度。
结论一:顺序执行的代码只会影响常数项,可以忽略。
结论二:只需挑循环中的一个基本操作分析它的执行次数与n的关系即可。
结论三:如果有多层嵌套循环,只需关注最深层循环了几次。
4、算法的存储空间需求
空间复杂度:空间开销(内存开销)与问题规模n之间的关系。

以空间复杂度作为算法所需存储空间的亮度,记作:
相关文章:
数据结构——绪论
一、绪论 (一)基本概念 数据:数据是对客观事物的符号表示,在计算机科学中是指所有能输入到计算机中并被计算机程序处理的符号的总称。 数据元素:数据元素是数据的基本单位,在计算机程序中通常作为一个整…...

Docker Dockerfile 语法与指令
一、简介 Docker 镜像原理、容器转成镜像 随便找个案例,进入 https://hub.docker.com/ 搜索 centos,然后随便找个版本(例如:centos7)点击一下,就会进入 centos7 的 dockerfile 文件: // 空镜像…...
【LeetCode每日一题】——566.重塑矩阵
文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【解题思路】八【时间频度】九【代码实现】十【提交结果】 一【题目类别】 矩阵 二【题目难度】 简单 三【题目编号】 566.重塑矩阵 四【题目描述】 在 MATLAB 中&…...

Manim(一款强大的数学可视化动画引擎)学习历程
相逢情便深,恨不相逢早 第一眼看见上面这种类型的视频我就深深被它的简约清楚所折服,我觉得它完全符合我的审美,我也相信只要了解过制作这种视频的软件的人都会喜欢上它。运用这种风格比较有名的是b站里的一位up主名叫3Blue1Brown࿰…...
powershell脚本写一个托盘图标
1、准备ico格式图标 star_bethlehem_icon 文件名改为star.ico 2、安装VSCode 如何下载安装VSCode 扩展:PowerShell扩展 3、创建项目 1、运行PowerShell命令 mkdir trayicon_ps1;cd trayicon_ps1;New-Item trayicon.ps1;code .2、将star.ico放入trayicon_ps1文…...
前端Vue入门-day08-vant组件库
(创作不易,感谢有你,你的支持,就是我前行的最大动力,如果看完对你有帮助,请留下您的足迹) 目录 vant 组件库 安装 导入 全部导入 按需导入 浏览器配饰 Viewport 布局 Rem 布局适配 vant 组件库 …...

华为OD机考--【磁盘容量排序】
■ 题目描述 【磁盘容量排序】 磁盘的容量单位常用的有M,G,T这三个等级,它们之间的换算关系为1T 1024G,1G 1024M,现在给定n块磁盘的容量, 请对它们按从小到大的顺序进行稳定排序,例如给定5…...

实现弧形切角两种方式
1、css 的 radial-gradient <view style"padding:30px; background: #ccc;"><view class"navActive"></view> </view>.navActive{width: 200px;height: 40px;background-color: #fff;color: rgb(0,63,136);position: relative;bor…...

什么是强化学习?
📝什么是强化学习? 1. 📝监督,非监督,强化2. 📝非 i.i.d3. 📝强化学习基本形式4. 📝马尔可夫过程 🌟 强化学习(Reinforcement Learning,RL&#x…...
如何在Linux系统上安装cpolar内网穿透
如何在Linux系统上安装cpolar内网穿透 文章目录 如何在Linux系统上安装cpolar内网穿透 cpolar作为一款体积小巧却功能强大的内网穿透软件,不仅能够在多种环境和应用场景中发挥巨大作用,还能适应多种操作系统,应用最为广泛的Windows、Mac OS系…...
分布式软件架构——内容分发网络
内容分发网络(CDN,Content Distribution Network或Content Delivery Network) 其基本思路是尽可能避开互联网上有可能影响数据传输速度和稳定性的瓶颈和环节,使内容传输得更快、更稳定。通过在网络各处放置节点服务器所构成的在现…...
【HAL库】STM32CubeMX开发----STM32F407----LAN8720A----移植FreeModbus实现ModbusTCP
前言 本次实验以 STM32F407VET6 芯片为MCU,使用 25MHz 外部时钟源。 以太网PHY层芯片为 LAN8720A,移植FreeModbus实现ModbusTCP网口通信。 具体内容参考文章:【HAL库】STM32CubeMX开发----STM32F407----ETHLAN8720ALWIP----ping通 本次移植…...

11-矩阵(matrix)_方阵_对称阵_单位阵_对角阵
矩阵及其运算 [ a 11 ⋯ a 1 n ⋯ ⋯ ⋯ a m 1 ⋯ a m n ] \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \cdots & \cdots & \cdots \\ a_{m1} & \cdots & a_{mn} \\ \end{bmatrix} a11⋯am1⋯⋯⋯a1n⋯amn 矩阵就是二维数组&…...
AWS多账户单点登录 IAM Identity Center(AWS SSO)
需求场景 多个aws账户,登陆麻烦且不安全,SSO单点功能并且外部身份提供者 — 如果您要管理外部身份提供者(IdP)(例如 Okta 或 Active Directory)中的用户。 官方文档:https://docs.aws.amazon.c…...
)
实验2-3-3 求奇数分之一序列前N项和 (15 分)
实验2-3-3 求奇数分之一序列前N项和 (15 分) 本题要求编写程序,计算序列 1 1/3 1/5 … 的前N项之和。 输入格式: 输入在一行中给出一个正整数N。 输出格式: 在一行中按照“sum S”的格式输出部分和的值S,精确到小数点后6位。…...

关于Android studio中的自动化测试脚本UiAutomator框架以及UiAutomatorViewer工具的使用——项目案例
加入依赖 implementation androidx.test.uiautomator:uiautomator:2.2.0创建CalcActivity页 <LinearLayout xmlns:android="http://schemas.android.com/apk/res/android"android:orientation="vertical"...

OA办公自动化系统设计与实现(论文+源码)_kaic
摘要 随着信息化建设的日益深入,无论是政府还是企事业单位,部门之间的信息沟通与协调工作越来越重要。人们迫切需要一个能充分利用网络优势,并可以管理企业的各种重要信息的软件平台,利用该平台快速建立自己的信息网络和办公管理系…...

ansible——playbook
playbook playbook是剧本的意思 通过 task 调用 ansible 的模块将多个 play 组织在一 个playbook中运行。 playbook本身由以下各部分组成: Tasks: 任务,即调用模块完成的某操作 Variables: 变量 Templates: 模板 Handlers: 处理器,当某条件…...
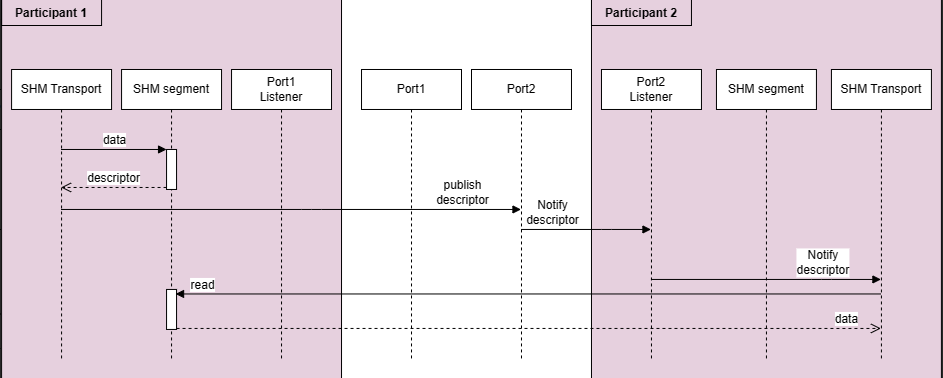
DDS中间件设计
OpenDDS、FastDDS数据分发服务中间件设计 软件架构 应用层DDS层RTPS层传输层 软件层次 FastDDS整体架构如下,这里可以看到DDS和RTPS的关系。另外缺少一部分IDL(统一描述语言),其应该是Pub、Sub的反序列化、序列化工具。 在RT…...

aws的EC2云服务器自己操作记录
亚马逊官网有免费试用1年的服务器 以下内容参考 1. 启动生成实例 1.1 创建实例时需要生成 使用的默认的 Debian 和 一个.pem后缀的秘钥 1.2 网上下一个Mobaxterm ,实例名是公有 IPv4 DNS 地址 ,使用SSH连接,登录名是admin 1.3 登录进去后 输入用户名 admin 后进去,sudo …...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...
