Vue中的组件渲染
在Vue中,组件的被渲染意味着将组件的内容转换为真实的DOM元素并添加到页面上。当Vue应用启动时,根组件会被渲染,并递归地渲染其子组件。
当组件被渲染时,Vue会将组件的模板解析成虚拟DOM(Virtual DOM)的形式。然后,Vue会比较虚拟DOM与实际DOM的差异,并将差异部分应用到页面上,以实现高效的DOM更新。
在组件被渲染后,组件的内容以及所包含的子组件会被转换为实际的HTML元素,并添加到页面的相应位置。
例如,我们在父组件的模板中使用子组件的标签,如下所示:
<template><div><h1>父组件</h1><ChildComponent /></div>
</template>当父组件被渲染时,<ChildComponent />会被转换为子组件ChildComponent的实际内容,并插入到父组件的DOM结构中。这样,子组件的模板内容就会在页面上展示出来。
因此,组件的被渲染是指将组件的内容转换为实际的DOM元素,并将其插入到页面中的过程。
相关文章:

Vue中的组件渲染
在Vue中,组件的被渲染意味着将组件的内容转换为真实的DOM元素并添加到页面上。当Vue应用启动时,根组件会被渲染,并递归地渲染其子组件。 当组件被渲染时,Vue会将组件的模板解析成虚拟DOM(Virtual DOM)的形…...
docker 保存和载入镜像
查看本机docker镜像 docker images保存镜像 docker save -o /home/space/work1/docker_qnx7.1.tar.gz a01ee6d74c36复制镜像到其他服务器 scp /home/space/work1/docker_qnx7.1.tar.gz XXXIP:/home/dell/work1/登录新 服务器操作 docker load -i docker_qnx7.1.tar.gz载入后…...
Java框架(九)--Spring Boot入门(1)
SpringBoot 2.x入门简介 学前基础 Maven Spring MVC理念 开发环境 Spring Boot官网版本介绍 https://spring.io/projects/spring-boot#learn 我们点击 Reference Doc. ,再点击Getting Started,就可以看到官网系统环境说明了 官网系统环境说明 Sp…...

2023年第四届“华数杯”数学建模思路 - 案例:随机森林
## 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 什么是随机森林? 随机森林属于 集成学习 中的 Bagging(Bootstrap AGgregation 的简称) 方法。如果用图来表示他们之…...

Redis中缓存穿透、击穿、雪崩以及解决方案
Redis中缓存穿透、击穿、雪崩以及解决方案 Redis作为一个高效的内存数据库,提供了缓存能力使得我们能够快速访问数据。然而,在使用Redis作为缓存时,我们可能会面临缓存穿透、缓存击穿和缓存雪崩的问题。接下来,我将详细解释这些现…...
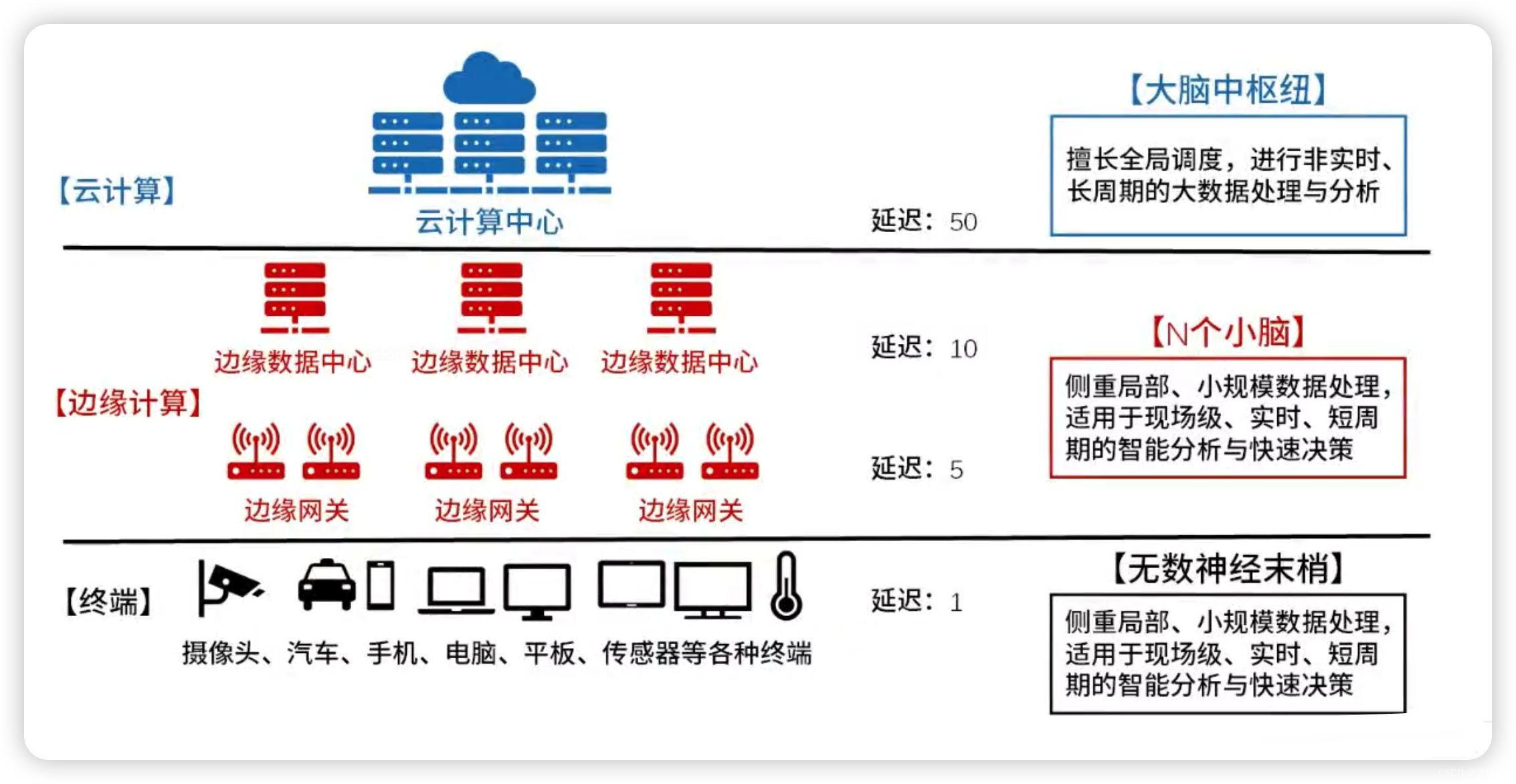
系统架构设计师-软件架构设计(6)
目录 一、物联网分层架构 二、大数据分层架构 三、基于服务的架构(SOA) 1、SOA的特征 2、服务构件与传统构件的区别 四、Web Service(WEB服务) 1、Web Services 和 SOA的关系 五、REST(表述性状态转移) 六、ESB(…...
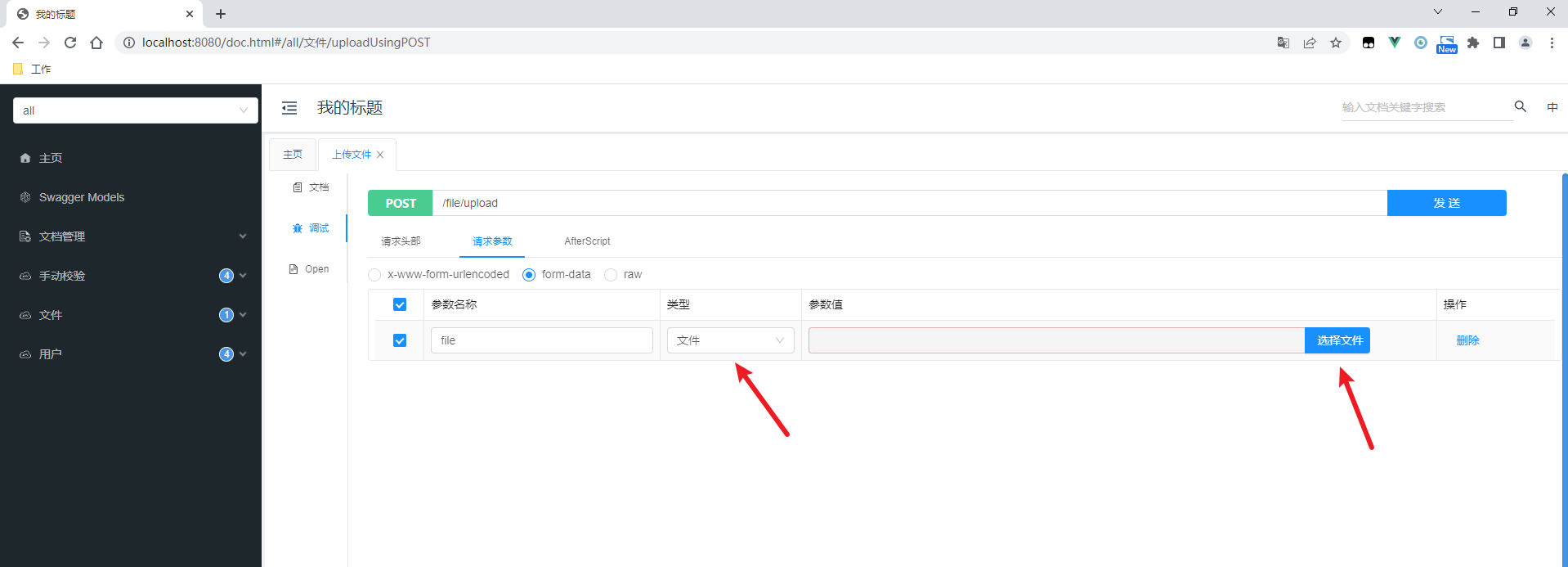
Knife4j系列--解决不显示文件上传的问题
原文网址:Knife4j系列--解决不显示文件上传的问题_IT利刃出鞘的博客-CSDN博客 简介 本文介绍使用Knife4j时无法上传文件的问题。 问题复现 依赖 <dependency><groupId>com.github.xiaoymin</groupId><artifactId>knife4j-spring-boot-…...

深入学习Mysql引擎InnoDB、MylSAM
目录 一、什么是MySQL 二、什么是InnoDB 三、什么是MyISAM 四、MySQL不同引擎有什么区别 一、什么是MySQL MySQL是一种广泛使用的开源关系型数据库管理系统(RDBMS),它是由瑞典MySQL AB公司开发并推广,后来被Sun Microsystems收…...

第七章:SpringMVC中
第七章:SpringMVC中 7.1:SpringMVC的视图 SpringMVC中的视图是View接口,视图的作用渲染数据,将模型Model中的数据展示给用户SpringMVC视图的种类很多,默认有转发视图和重定向视图。 当工程引入jstl的依赖&…...
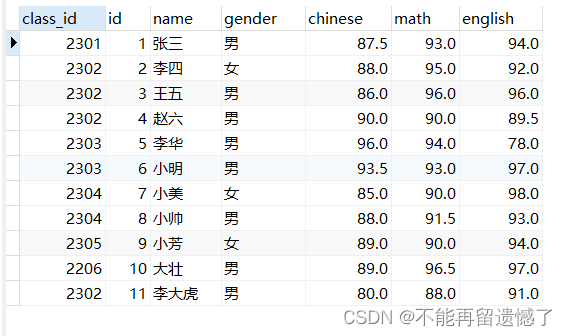
MySQL数据库——DQL操作——基本查询
文章目录 前言事前准备——测试数据整表查询指定列查找别名查询MySQL运算符条件查询模糊查询排序查询聚合查询分组查询分组之后的条件筛选 分页查询将整张表的数据插入到另一张表中 前言 MySQL数据库常见的操作是增删查改,而其中数据的查询是使用最多,也…...
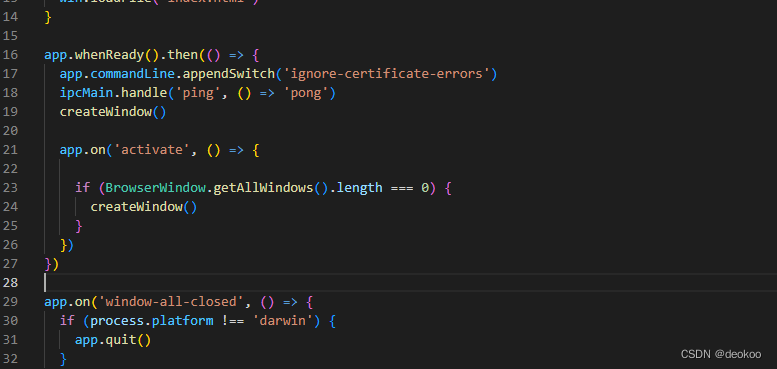
Electron 开发,报handshake failed; returned -1, SSL error code 1,错误
代码说明 在preload.js代码中,暴露参数给渲染线程renderer.js访问, renderer.js 报:ERROR:ssl_client_socket_impl.cc(978)] failed; returned -1, SSL error code 1,错误 问题原因 如题所说,跨进程传递消息,这意味…...
知识区博主转型——兼做知识区和改造区博主!!!!!
想脱单的进来,一起交流如何能脱单!!! 为什么——我太羡慕有对象的人了哭死!!!!!! 你是不是很羡慕别人怎么都有女朋友 别人家的女朋友怎么都那么好ÿ…...

Resnet与Pytorch花图像分类
1、介绍 1.1数据集介绍 flower_data├── train│ └── 1-102(102个文件夹)│ └── XXX.jpg(每个文件夹含若干张图像)├── valid│ └── 1-102(102个文件夹)└── ─── └── XXX.jp…...
)
【NLP概念源和流】 03-基于计数的嵌入,GloVe(第 3/20 部分)
接续上文 【NLP概念源和流】 02-稠密文档表示(第 2/20 部分)...

【React】关于组件之间的通讯
🌟组件化:把一个项目拆成一个一个的组件,为了便与开发与维护 组件之间互相独立且封闭,一般而言,每个组件只能使用自己的数据(组件状态私有)。 如果组件之间相互传参怎么办? 那么就要…...
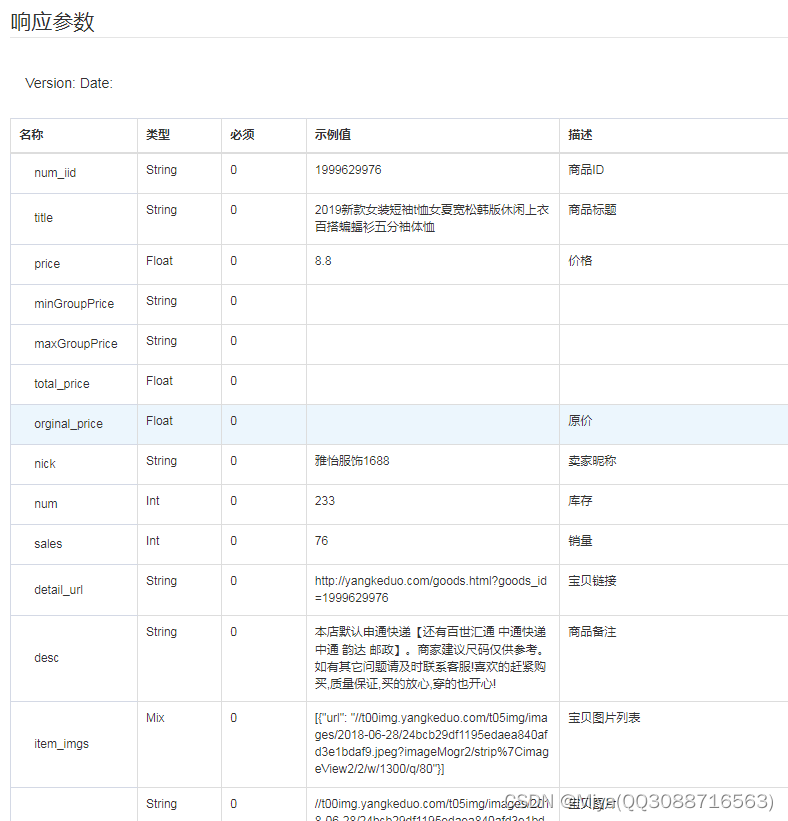
item_get-小红薯-商品详情
一、接口参数说明: smallredbook.item_get,点击更多API调试,请移步注册API账号点击获取测试key和secret 公共参数 请求地址: https://api-gw.onebound.cn/smallredbook/item_get 名称类型必须描述keyString是调用key(http://o0…...
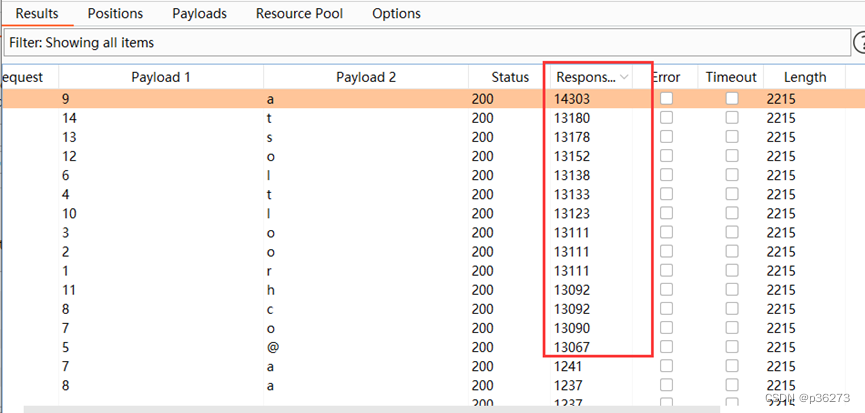
网络安全进阶学习第十课——MySQL手工注入
文章目录 一、MYSQL数据库常用函数二、MYSQL默认的4个系统数据库以及重点库和表三、判断数据库类型四、联合查询注入1、具体步骤(靶场演示):1)首先判断注入点2)判断是数字型还是字符型3)要判断注入点的列数…...

2.3 网络安全协议
数据参考:CISP官方 目录 OSI七层模型TCP/IP体系架构TCP/IP安全架构 一、OSI七层模型 简介 开放系统互连模型(Open System Interconnection Reference Model,OSI)是国际标准化组织(ISO)于1977年发布的…...

Apache Flink概述
Flink 是构建在数据流之上的一款有状态的流计算框架,通常被人们称为第三代大数据分析方案 第一代大数据处理方案:基于Hadoop的MapReduce 静态批处理 | Storm 实时流计算 ,两套独立的计算引擎,难度大(2014年9月&#x…...
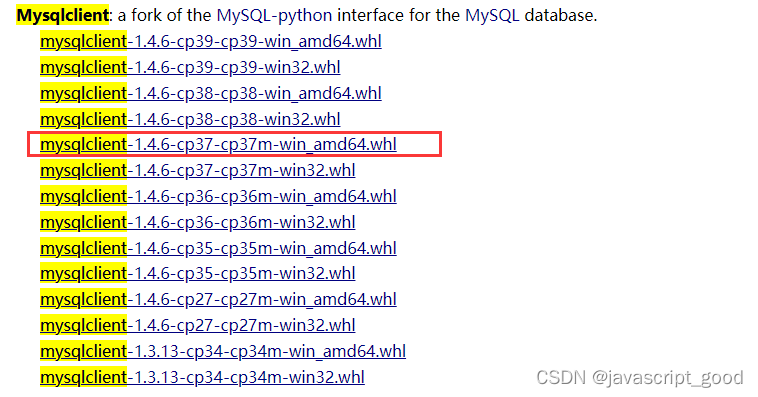
django使用mysql数据库
Django开 发操作数据库比使用pymysql操作更简单,内部提供了ORM框架。 下面是pymysql 和orm操作数据库的示意图,pymysql就是mysql的驱动,代码直接操作pymysql ,需要自己写增删改查的语句 django 就是也可以使用pymysql、mysqlclient作为驱动&a…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...
