用于永磁同步电机驱动器的自适应SDRE非线性无传感器速度控制(MatlabSimulink实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码&Simulink仿真实现
💥1 概述
本文方法基于状态依赖的里卡蒂方程(SDRE)控制技术及其梯度型神经网络的实时计算方法,允许在线控制PMSM。
为了实现用于永磁同步电机驱动器的自适应 SDRE(State-Dependent Riccati Equation)非线性无传感器速度控制,按照以下步骤进行。
1. 确定系统的动态模型:首先,获得永磁同步电机的动态模型。该模型通常由磁链方程、电流方程和机械方程等组成。根据电机的具体参数和特性,推导出系统的状态空间表达式。
2. 设计自适应 SDRE 控制器:基于系统的状态空间表达式,采用自适应 SDRE 控制策略进行设计。自适应 SDRE 控制是一种基于 Riccati 方程调节器的非线性控制方法,它通过自适应参数来优化控制器的性能。具体设计步骤包括:设置控制器结构、定义控制误差目标和性能指标、计算状态反馈增益矩阵和 Riccati 方程解。
3. 实现无传感器速度估计器:由于无传感器速度控制,需要通过估计器来获取电机转速的信息。可以采用滑模观测器或者其他速度估计器来实现,以获得无传感器的速度测量。
4. 连接控制器和估计器:将自适应 SDRE 控制器和无传感器速度估计器与电机的动态模型相连接。确保控制器能够接收估计到的速度信号,并提供相应的控制输出。
5. 仿真和调试:在 Simulink 环境中建立仿真模型,并进行仿真验证。通过逐步参数调整和性能评估,对控制系统进行调试和优化。
📚2 运行结果
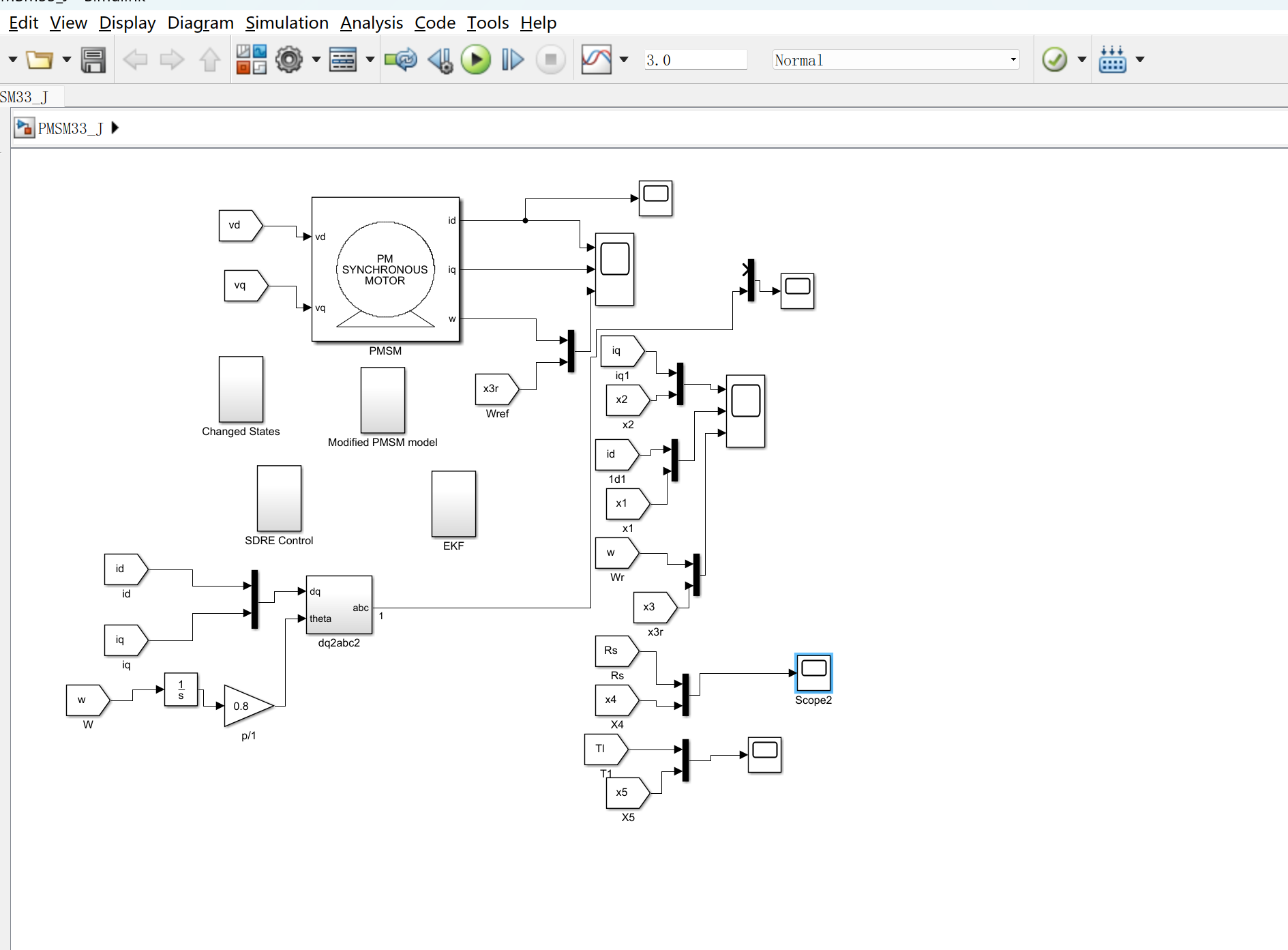
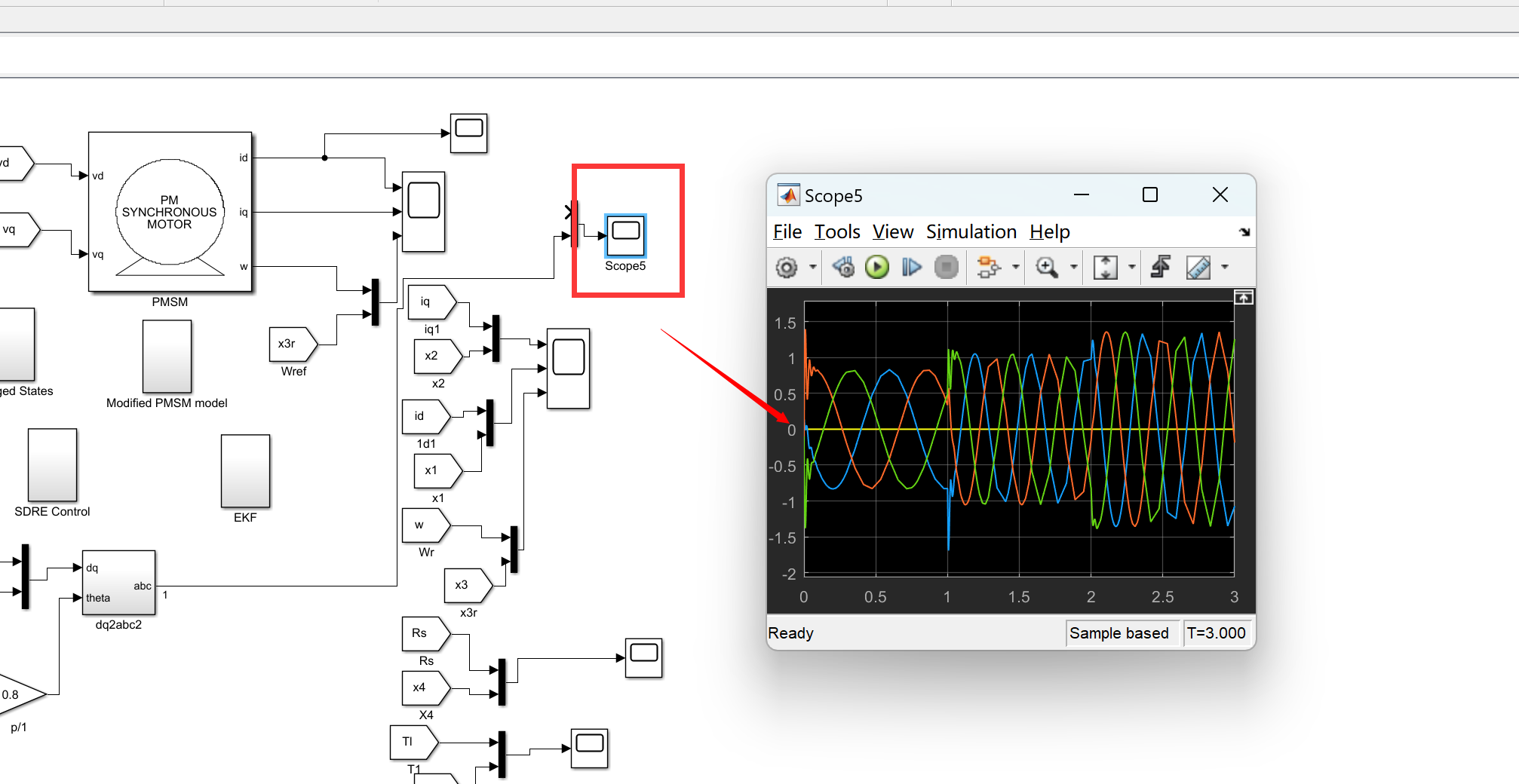
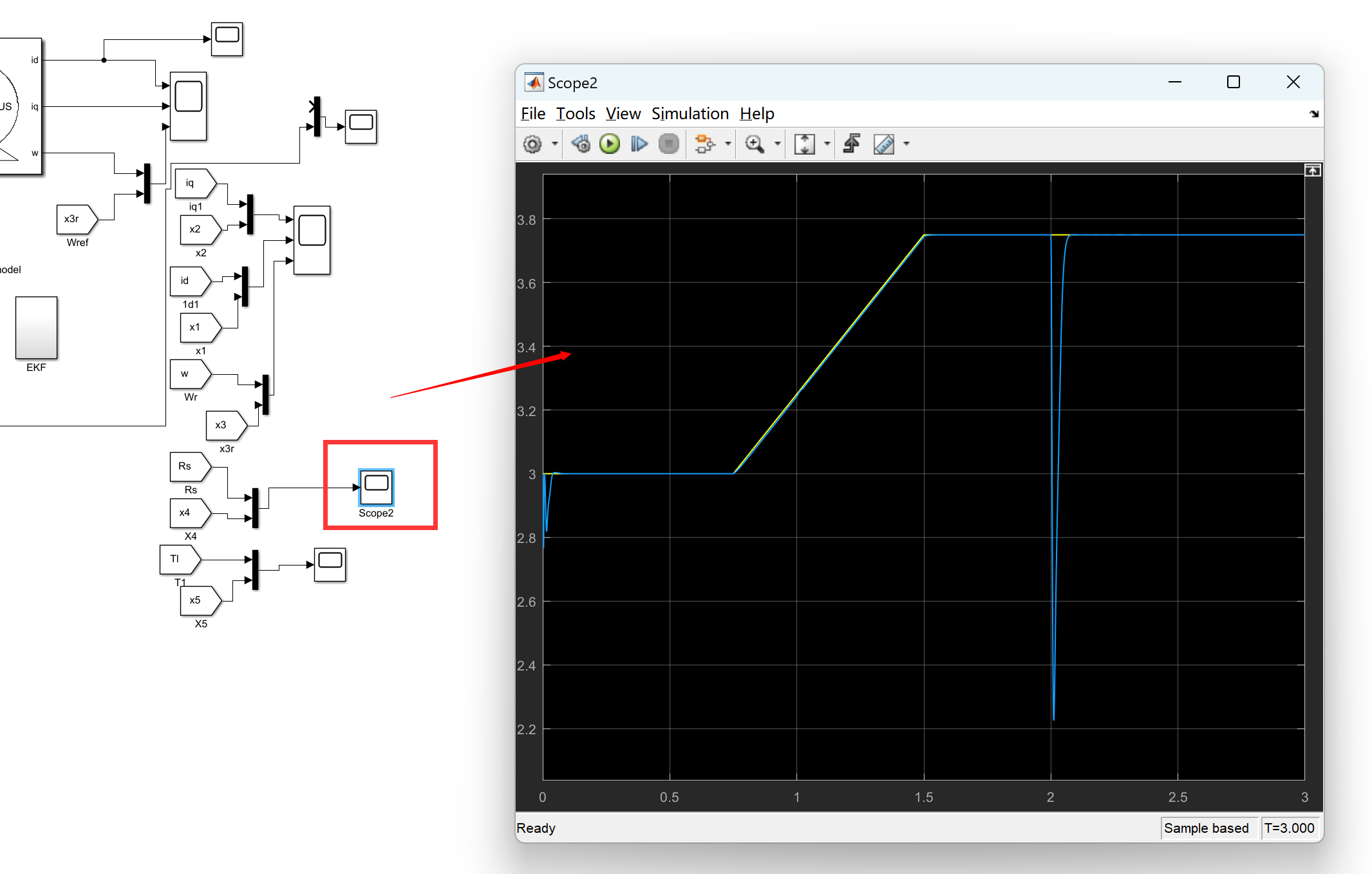
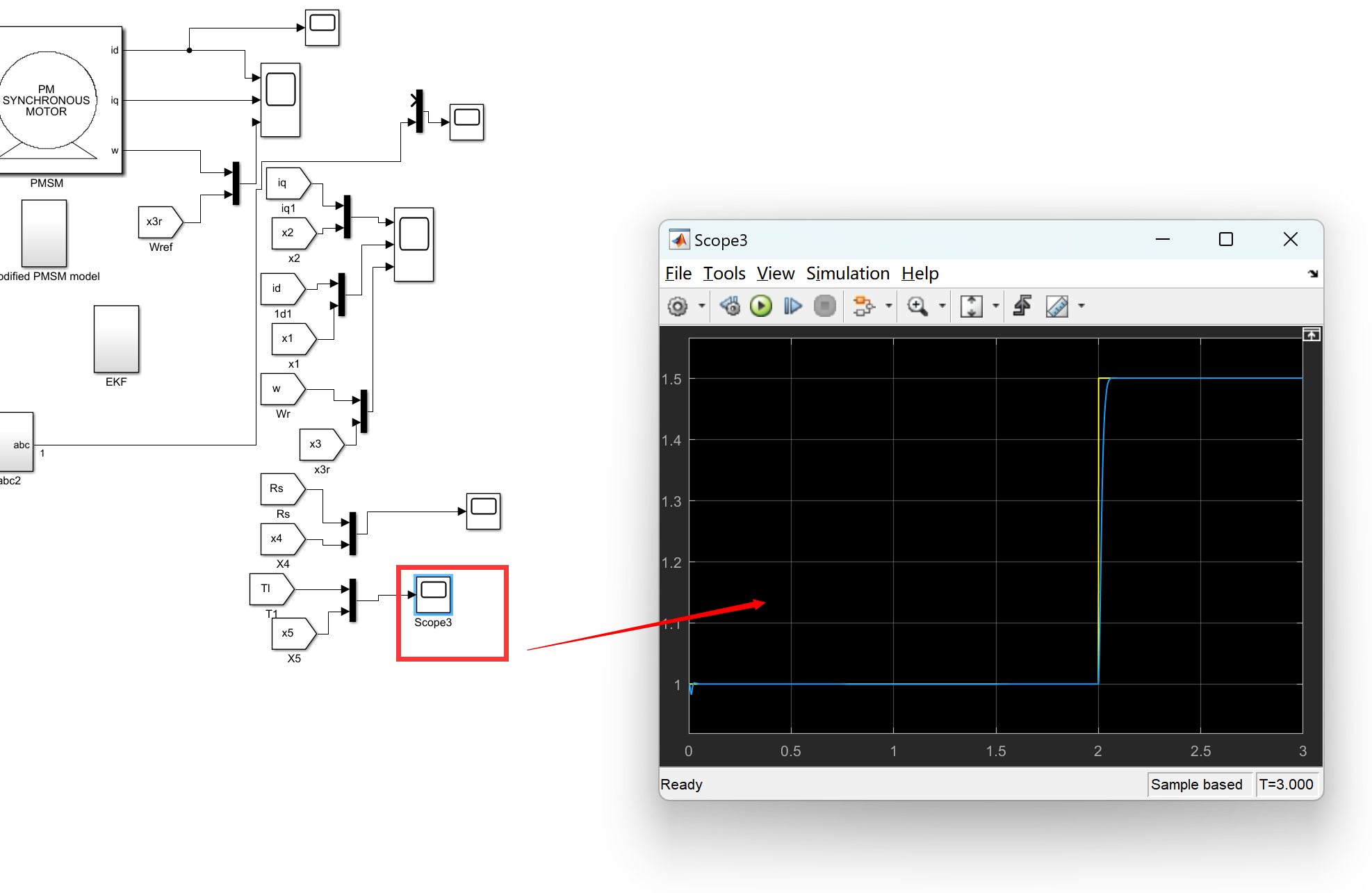
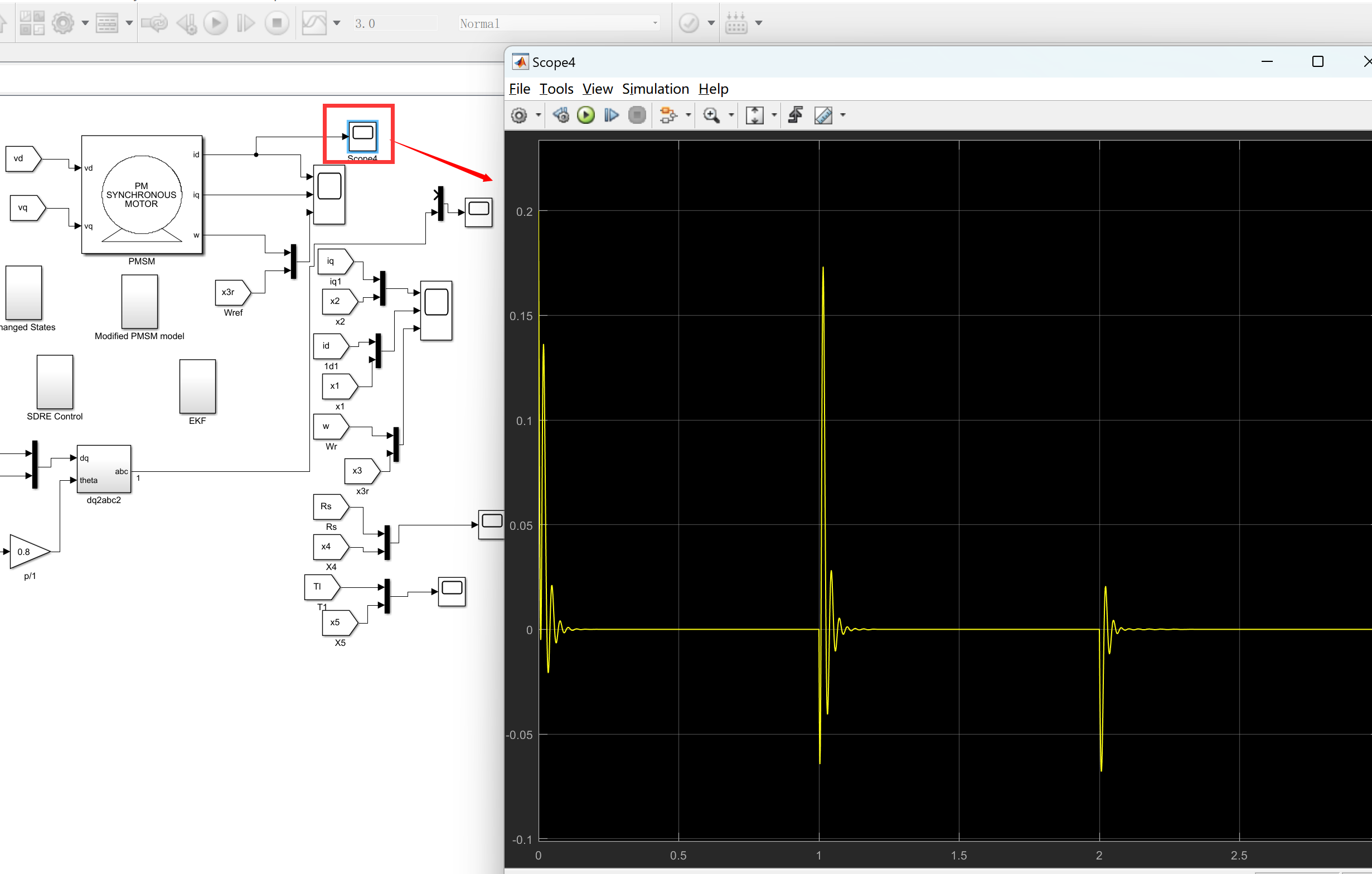

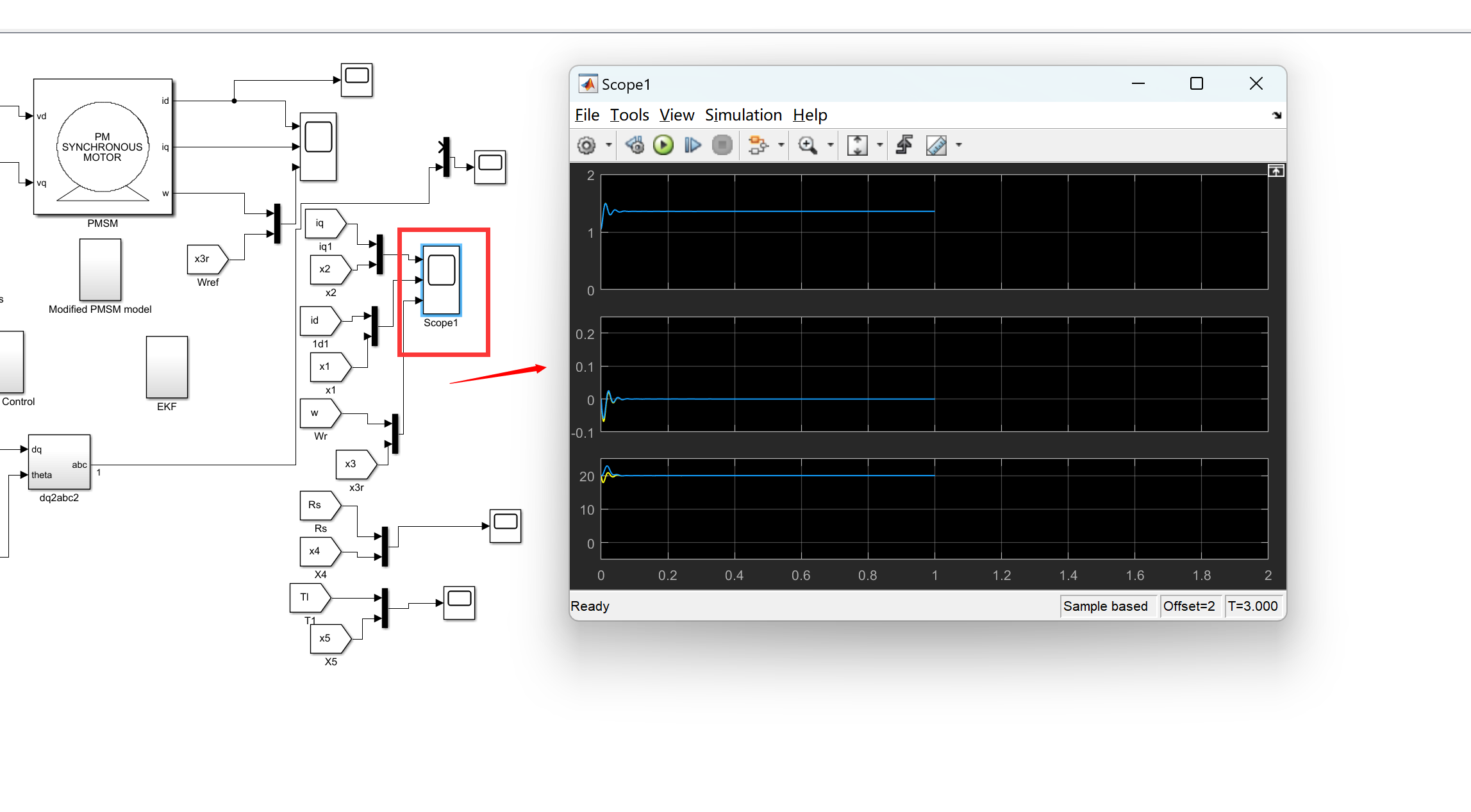 matlab程序:
matlab程序:
clc
clear all
Rs=0.625
Ld=0.036
Lq=0.051
phi=0.545
J=7.5e-4
F=0.036
P=2
% a1=R/Ld
a2=P*Lq/Ld
a3=P*Ld/Lq
% a4=R/Lq
a5=P*phi/Lq
a6=3/2*P*phi/J
a7=F/J
B=[1 0;0 1;0 0]
Qc=[1 0 0;0 1 0;0 0 1]
R=[1 0;0 10]
x2dot=0
x3dot=0
gama=0.1
% syms a1 a2 a3 a4 a5 a6 a7 x1 x2 x3 R
% f=[-a1*R*x1+a2*x2*x3; -a3*x1*x3-a4*R*x2-a5*x3; a6*x2-a7*x3-1/J*Tl;0]
% jacobian(f,[x1 x2 x3 R ])
% E=4300170000*[1e-6 0 0 0 ;0 1e-6 0 0 ;0 0 1e-6 0 ;0 0 0 1e-6 ]
Rk=0.09*[1 0;0 1]
E=4300180000*[1e-6 0 0 0 0 ;0 1e-6 0 0 0 ;0 0 1e-6 0 0 ;0 0 0 1e-2 0; 0 0 0 0 1e-5]
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]刘伟波,邢佳丽,赵向禹等.双三相多相永磁同步电机驱动器混合直接转矩控制策略[J].科学技术与工程,2022,22(09):3564-3575.
[2]黄义红,张峻涛,刘丹. 机载永磁同步电机驱动器电流重构设计[C]//中国航空学会.第五届中国航空科学技术大会论文集.北京航空航天大学出版社(BEIHANG UNIVERSITY PRESS),2021:592-596.DOI:10.26914/c.cnkihy.2021.064916.
[3]凌峰. 无轴承异步电机非线性解耦控制与无传感器控制研究[D].江苏大学,2021.DOI:10.27170/d.cnki.gjsuu.2021.001911.
[4]江俊. 基于非线性估计理论的永磁同步电机无传感器控制方法的研究[D].江南大学,2006.
🌈4 Matlab代码&Simulink仿真实现
相关文章:

用于永磁同步电机驱动器的自适应SDRE非线性无传感器速度控制(MatlabSimulink实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
Spring Cloud+Spring Boot+Mybatis+uniapp+前后端分离实现知识付费平台免费搭建 qt
Java版知识付费源码 Spring CloudSpring BootMybatisuniapp前后端分离实现知识付费平台 提供职业教育、企业培训、知识付费系统搭建服务。系统功能包含:录播课、直播课、题库、营销、公司组织架构、员工入职培训等。 提供私有化部署,免费售…...
删除注释(力扣)
删除注释 题目 给一个 C 程序,删除程序中的注释。这个程序source是一个数组,其中source[i]表示第 i 行源码。 这表示每行源码由 ‘\n’ 分隔。 在 C 中有两种注释风格,行内注释和块注释。 字符串// 表示行注释,表示//和其右侧…...

阿里云AK创建
要在阿里云上创建 Access Key(AK),您需要按照以下步骤进行操作: 登录到阿里云控制台([https://www.aliyun.com/?utm_contentse_1014243503))。 点击右上方的主账号,点击“AccessKey管理”。 …...

OC与Swift的相互调用
OC调用Swift方法 1、在 Build Settings 搜索 Packaging ,设置 Defines Module 为 YES 2、新建 LottieBridge.swift 文件,自动生成桥 ProductName-Bridging-Header.h 3、在 LottieBridge.swift 中,定义Swift类继承于OC类,声明 obj…...

某银行软件测试笔试题
(时间90分钟,满分100分) 考试要求:计算机相关专业试题 一、填空题(每空1分,共10分) 1. ______验证___是保证软件正确实现特定功能的一系列活动和过程。 2. 按开发阶段分,软件测试可…...

SpringMVC概述、SpringMVC的工作流程、创建SpringMVC的项目
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaweb 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 Spring MVC入门 一、Spring MVC概述二、入门案例2.1导入Sp…...

一文说清楚支付架构
作者:陈斌 支付的技术架构是为了保障能够顺利处理支付请求而设计的结构体系。从系统的角度看,它包括了计算机系统的软件、硬件、网络和数据等。从参与的主体角度来看,它涉及交易的付款方、收款方、支付机构、银行、卡组织和金融监管机构等。要…...

【Golang 接口自动化00】为什么要用Golang做自动化?
目录 为什么使用Golang做自动化 最终想实现的效果 怎么做? 写在后面 资料获取方法 为什么使用Golang做自动化 顺应公司的趋势学习了Golang之后,因为没有太多时间和项目来实践,怕止步于此、步Java缺少练习遗忘殆尽的后尘,决定…...
Android 架构模式如何选择
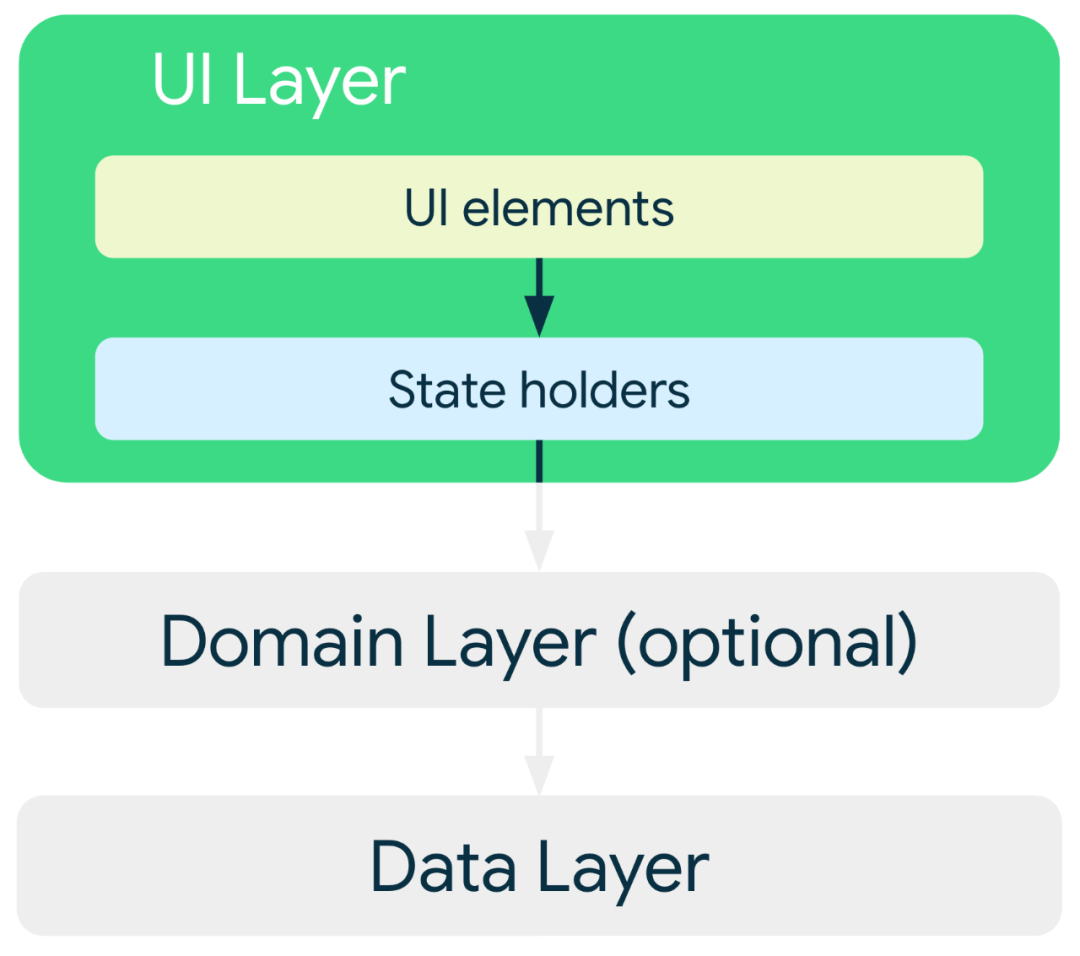
作者:vivo 互联网客户端团队-Xu Jie Android架构模式飞速演进,目前已经有MVC、MVP、MVVM、MVI。到底哪一个才是自己业务场景最需要的,不深入理解的话是无法进行选择的。这篇文章就针对这些架构模式逐一解读。重点会介绍Compose为什么要结合MV…...

深入了解 LoRaWAN® B 类设备
介绍 在 LoRaWAN 网络中,终端设备以三种模式之一运行:LoRaWAN A 类、B 类和 C 类。网络只能将消息(下行链路)发送到终端设备在两个短接收窗口之一期间处于 A 类模式,该接收窗口在设备向网络发送消息(上行链路)后立即打开。然而,这些上行链路不是预先安排的,并且可以由…...
KK集团再闯港交所:引领潮流零售市场,2023年一季度业绩增势显著
撰稿|行星 来源|贝多财经 7月31日,KK Group Company Holdings Limited(下称“KK集团”)在港交所更新招股书,补充了截至2023年3月31日的财务数据等信息,继续推进上市事宜,摩根士丹利和瑞信为其联席保荐人。…...

Vue中的组件渲染
在Vue中,组件的被渲染意味着将组件的内容转换为真实的DOM元素并添加到页面上。当Vue应用启动时,根组件会被渲染,并递归地渲染其子组件。 当组件被渲染时,Vue会将组件的模板解析成虚拟DOM(Virtual DOM)的形…...
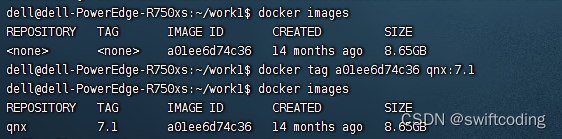
docker 保存和载入镜像
查看本机docker镜像 docker images保存镜像 docker save -o /home/space/work1/docker_qnx7.1.tar.gz a01ee6d74c36复制镜像到其他服务器 scp /home/space/work1/docker_qnx7.1.tar.gz XXXIP:/home/dell/work1/登录新 服务器操作 docker load -i docker_qnx7.1.tar.gz载入后…...
Java框架(九)--Spring Boot入门(1)
SpringBoot 2.x入门简介 学前基础 Maven Spring MVC理念 开发环境 Spring Boot官网版本介绍 https://spring.io/projects/spring-boot#learn 我们点击 Reference Doc. ,再点击Getting Started,就可以看到官网系统环境说明了 官网系统环境说明 Sp…...

2023年第四届“华数杯”数学建模思路 - 案例:随机森林
## 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 什么是随机森林? 随机森林属于 集成学习 中的 Bagging(Bootstrap AGgregation 的简称) 方法。如果用图来表示他们之…...

Redis中缓存穿透、击穿、雪崩以及解决方案
Redis中缓存穿透、击穿、雪崩以及解决方案 Redis作为一个高效的内存数据库,提供了缓存能力使得我们能够快速访问数据。然而,在使用Redis作为缓存时,我们可能会面临缓存穿透、缓存击穿和缓存雪崩的问题。接下来,我将详细解释这些现…...
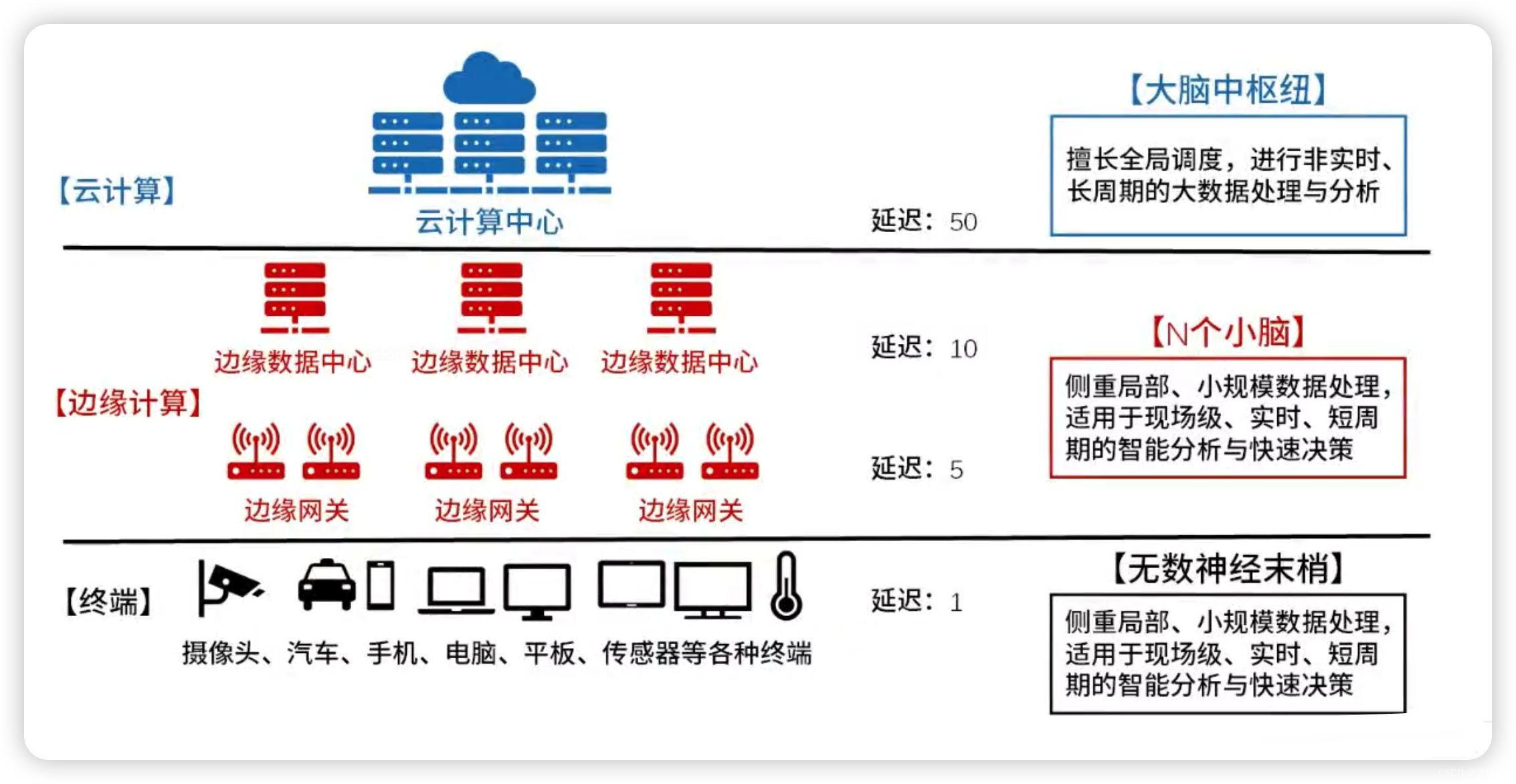
系统架构设计师-软件架构设计(6)
目录 一、物联网分层架构 二、大数据分层架构 三、基于服务的架构(SOA) 1、SOA的特征 2、服务构件与传统构件的区别 四、Web Service(WEB服务) 1、Web Services 和 SOA的关系 五、REST(表述性状态转移) 六、ESB(…...
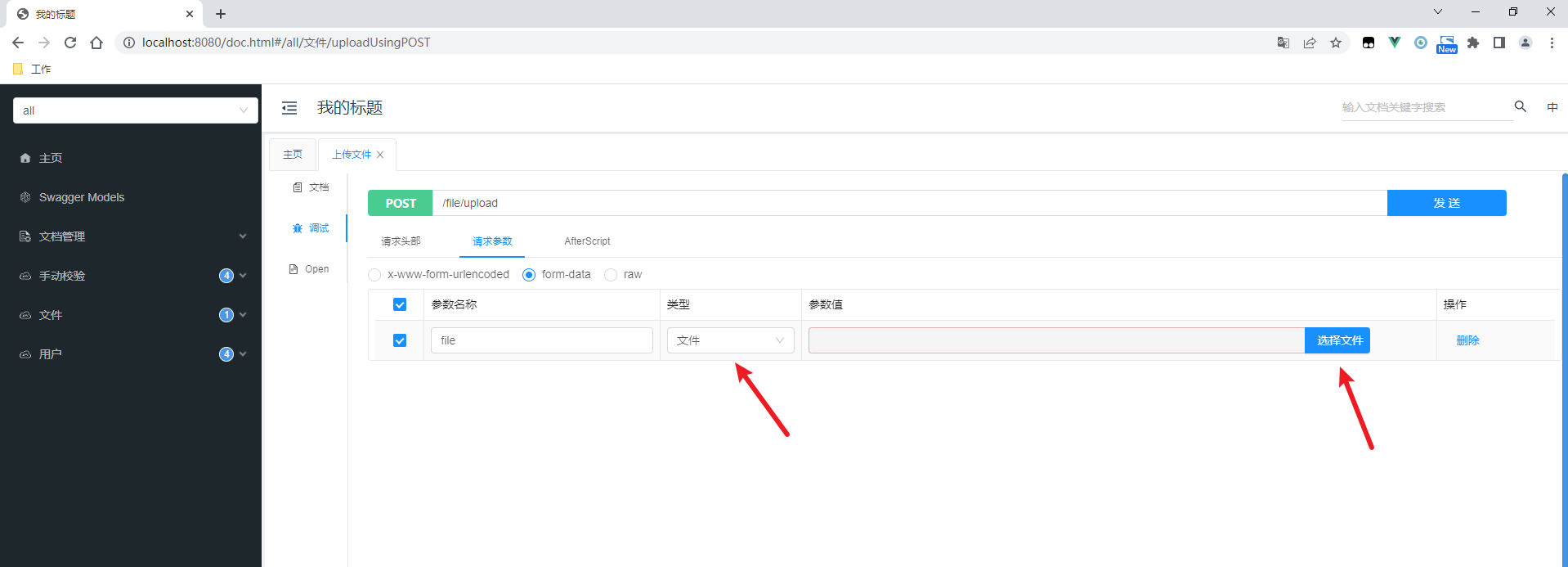
Knife4j系列--解决不显示文件上传的问题
原文网址:Knife4j系列--解决不显示文件上传的问题_IT利刃出鞘的博客-CSDN博客 简介 本文介绍使用Knife4j时无法上传文件的问题。 问题复现 依赖 <dependency><groupId>com.github.xiaoymin</groupId><artifactId>knife4j-spring-boot-…...

深入学习Mysql引擎InnoDB、MylSAM
目录 一、什么是MySQL 二、什么是InnoDB 三、什么是MyISAM 四、MySQL不同引擎有什么区别 一、什么是MySQL MySQL是一种广泛使用的开源关系型数据库管理系统(RDBMS),它是由瑞典MySQL AB公司开发并推广,后来被Sun Microsystems收…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

