实数信号的傅里叶级数研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
实数信号的傅里叶级数是将实数信号分解为一系列正弦和余弦函数的和。通过研究实数信号的傅里叶级数,我们可以揭示信号的频域特性、谐波成分以及信号的周期性等信息。
以下是实数信号的傅里叶级数研究的步骤:
1. 确定信号的周期:实数信号的傅里叶级数要求信号是周期性的,因此第一步是确定信号的周期。如果信号已知周期,则直接使用已知的周期;如果信号的周期未知,可以通过观察信号的重复性或通过分析信号的特征来估计周期。
2. 计算基频和谐波频率:基频是指信号的周期的倒数,而谐波频率是基频的整数倍。通过计算基频和谐波频率,可以确定傅里叶级数中需要考虑的频率分量。
3. 计算信号的系数:使用傅里叶级数的公式,根据信号的周期和所选的频率分量,计算信号在每个频率分量上的系数。系数表示了每个频率分量对于信号的贡献程度。
4. 重构信号:将计算得到的正弦和余弦函数按照其对应的系数加权求和,可以重构出原始信号的近似,即使用傅里叶级数近似表示原始信号。
5. 分析频域特性和谐波成分:通过观察每个频率分量的系数,可以了解信号在频域上的特性。特别是谐波成分在系数中的存在可以揭示信号中的谐波结构和频率分布情况。
6. 评估和调整:根据计算得到的傅里叶级数近似信号和频域分析结果,评估傅里叶级数的逼近效果,并进行必要的调整和优化。
需要注意的是,实数信号的傅里叶级数研究需要信号是周期性的。对于非周期信号,可以考虑使用傅里叶变换进行频域分析。
总之,实数信号的傅里叶级数研究包括确定信号的周期、计算基频和谐波频率、计算信号的系数、重构信号、分析频域特性和谐波成分等步骤。通过这些步骤,我们可以深入了解信号的频域特性和谐波成分,从而更好地理解和处理实数信号。
📚2 运行结果

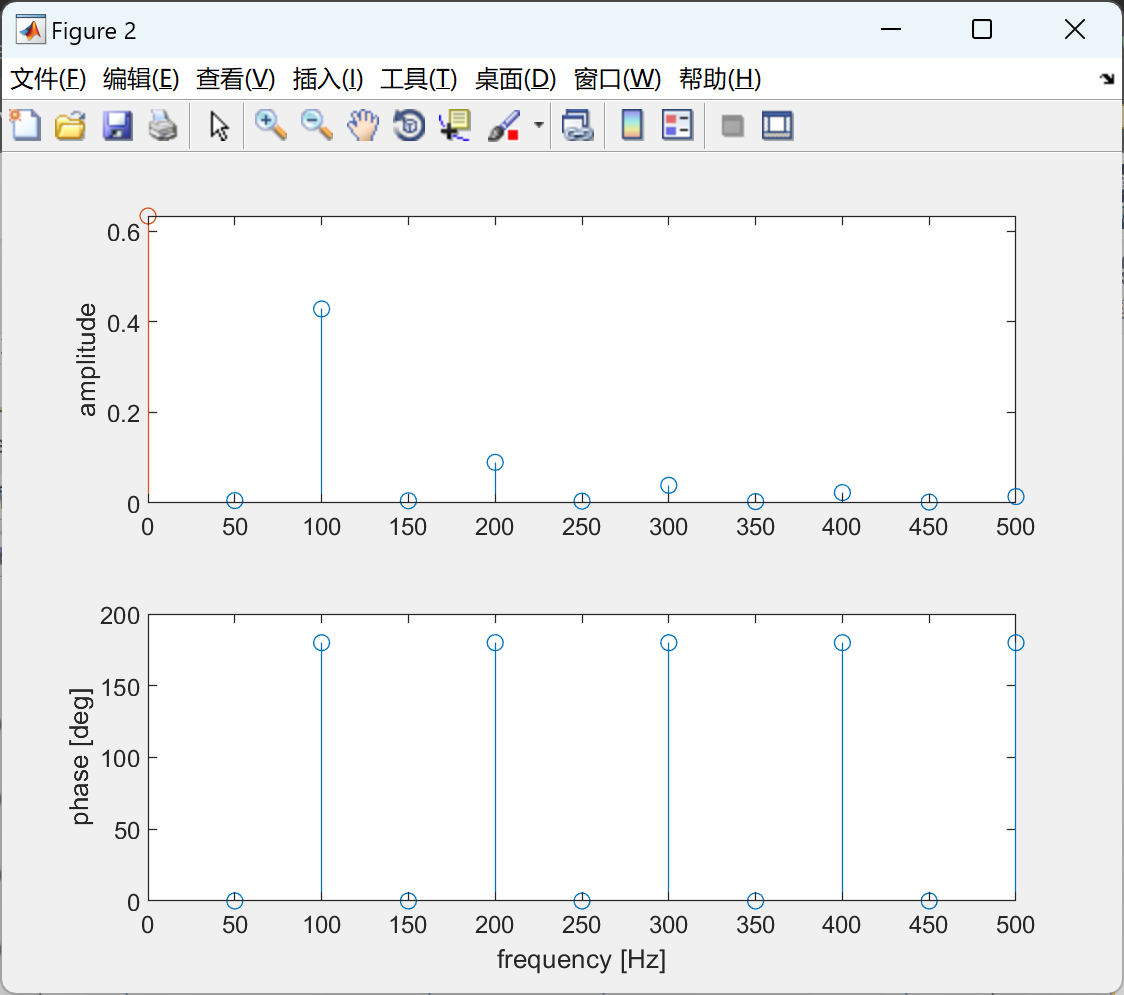
部分代码:
function [ freq,amp,phase,dc ] = fourier_series_real( t,x )
% function [ freq,amp,phase,dc ] = fourier_series_real( t,x )
% Fourier series of real signals.
% Written by Yoash Levron, January 2013.
%
% This function computes the fourier series of a signal x(t).
% the amplitudes of the fourier series have the same dimension
% of the original signal, so this function is useful for immediate
% computation of the actual frequency components, without
% further processing.
%
% for example, x(t) = 2 + 3*cos(2*pi*50*t) will result in
% dc value = 2
% frequencies = [50 100 150 200 ...]
% amplitudes = [3 0 0 0 ...]
% phases = [0 0 0 0 ...]
%
% x(t) is one cycle of an infinite cyclic signal. The function
% computes the fourier transform of that infinite signal.
% the period of the signal (T) is determined by the length
% of the input time vector, t.
% x(t) must be real (no imaginary values).
%
% The signal x(t) is represented as:
% x(t) = Adc + A1*cos(w*t + ph1) + A2*cos(2*w*t + ph2) + ...
% the function computes the amplitudes, Adc,A1,A2...
% and the phases ph1,ph2,...
%
% T = period of the signal = t(end) - t(1)
% w = basic frequency = 2*pi/T
%
% The function automatically interpolates the original signal
% to avoid aliasing. Likewise, the function automatically determines
% the number of fourier components, and truncates trailing zeros.
%
% inputs:
% t - [sec] time vector. Sample time may vary within the signal.
% x - signal vector. same length as t.
%
% outputs:
% freq - [Hz] frequencies of the fourier series, not including zero.
% amp - amplitudes vector. amp=[A1 A2 A3 ...], not including the DC component.
% phase - [rad/sec] . phases, not including the DC component.
% dc - the DC value (average of the signal).
%%%%%%%%%%% computation %%%%%%%%
rel_tol = 1e-4; % relative tolerance, to determine trailing zero truncation
if (~isreal(x))
clc;
beep;
disp('fourier_series_real Error: x(t) must be real.');
dc = NaN; amp = NaN; freq = NaN; phase = NaN;
return;
end
t = t-t(1); % shifting time to zero.
T = t(end); % period time.
N = 100; % number of samples
if (mod(N,2) == 1)
N = N + 1;
end
N = N/2;
ok = 0;
while (~ok)
N = N*2; % increase number of samples
if (N > 10e6)
clc;
beep;
disp('fourier_series_real Error: signal bandwidth seems too high.');
disp('Try decreasing the sample time in the input time vector t,');
disp('or increasing the relative tolerance rel_tol');
dc = NaN; amp = NaN; freq = NaN; phase = NaN;
return;
end
dt = T/N;
t1 = 0:dt:(T-dt);
x1 = interp1(t,x,t1,'cubic',0);
xk = (1/N)*fft(x1);
dc = abs(xk(1));
xkpos = xk(2:(N/2));
xkneg = xk(end:-1:(N/2+2));
freq = [1:length(xkpos)]/T; % Hz
amp = 2*abs(xkpos);
phase = angle(xkpos); % rad/sec
%%% check if enough samples are used.
%%% if not, try again, with more samples.
Am = max(amp);
ii = find((amp(end-10:end)/Am)>rel_tol);
ok = isempty(ii);
end
% %%% truncate output vectors to remove trailing zeros
Am = max(amp);
ii = length(amp);
while (amp(ii) < Am*rel_tol)
ii = ii - 1;
end
amp = amp(1:ii);
freq = freq(1:ii);
phase = phase(1:ii);
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]赵乐源,刘传辉,刘锡国等.基于傅里叶级数的椭圆球面波信号时频分析[J].现代电子技术,2022,45(17):35-40.DOI:10.16652/j.issn.1004-373x.2022.17.007.
[2]苗永平,代坤,陈达等.傅里叶级数实验的优化设计与实践[J].实验室科学,2021,24(06):1-4+9.
🌈4 Matlab代码实现
相关文章:

实数信号的傅里叶级数研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

oracle数据库巡检脚本
用于Oracle数据库巡检的示例脚本: #!/bin/bash# 设置数据库连接信息 DB_USER="your_db_username" DB_PASSWORD="your_db_password" DB_HOST="your_db_host" DB_PORT="your_db_port" DB_SID="your_db_sid" OUTPUT_FILE=&q…...
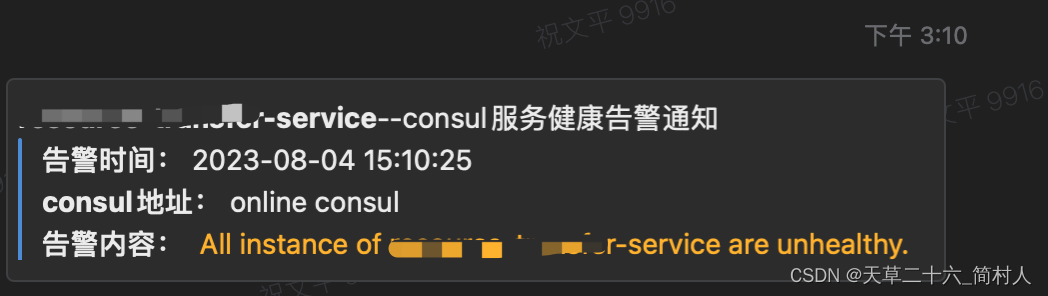
服务注册中心consul的服务健康监控及告警
一、背景 consul既可以作为服务注册中心,也可以作为分布式配置中心。当它作为服务注册中心的时候,java微服务之间的调用,会定期查询服务的实例列表,并且实例的状态是健康可用。 如果发现被调用的服务,注册到consul的…...

【算法第十四天7.28】二叉树的最大深度,二叉树的最小深度 ,完全二叉树的节点个数
链接力扣104-二叉树的最大深度 思路 class Solution {public int maxDepth(TreeNode root) {if(root null) return 0;if(root.left null) return maxDepth(root.right) 1;if(root.right null) return maxDepth(root.left) 1;int max Math.max(maxDepth(root.left),maxD…...

网络安全设备-等保一体机
本文为作者学习文章,按作者习惯写成,如有错误或需要追加内容请留言(不喜勿喷) 本文为追加文章,后期慢慢追加 等保一体机的功能 等保一体机产品主要依赖于其丰富的安全网元(安全网元包括:防火…...

Kafka的配置和使用
目录 1.服务器用docker安装kafka 2.springboot集成kafka实现生产者和消费者 1.服务器用docker安装kafka ①、安装docker(docker类似于linux的软件商店,下载所有应用都能从docker去下载) a、自动安装 curl -fsSL https://get.docker.com | b…...

【C++】unordered_map在Windows和Linux上的不同行为
我目前手头上的项目,需要编译在板端Linux上运行,但是日常daily调试多在Windows上开发。这就涉及到同一份代码在多平台上的编译个运行。有一次遇到了一个奇怪的现象:跑同样的一份代码,Windows和Linux出来的结果是不一致的。最终确定…...
Apipost三方消息通知,接口变更不用愁
Apipost致力于为开发者提供更全面的API管理功能。而最近,Apipost又新增了一个非常实用的功能:第三方消息推送。这个功能可以帮助开发人员及时了解API的变更情况,从而更好地管理和优化自己的API。 具体来说,Apipost的第三方消息推…...
C语言 用数组名作函数参数
当用数组名作函数参数时,如果形参数组中各元素的值发生变化,实参数组元素的值随之变化。 1.数组元素做实参的情况: 如果已经定义一个函数,其原型为 void swap(int x,int y);假设函数的作用是将两个形参(x,y…...
-回溯)
每日一题(980. 不同路径 III)-回溯
题目 980. 不同路径 III 题解思路 表格中值为1的为起始点值为0 的是可以经过的点,但是只能经过一次值为2 的是终点,计算从起点到终点一共有多少种路径 计算出值为0的方格个数,同时找到起点位置当位于终点时候且经过所有的方格为0的点 即为…...
, loads(), dump(), dumps())
【Python:json常用函数,用于加载和保存json文件】load(), loads(), dump(), dumps()
文章目录 1、load()2、loads()3、dump()4、dumps() json文件为javascript object Notation文件,属于轻量级的数据交换格式,可以用于存储和交换数据。json文件是由类似{ }的key-value映射组成。 1、load() 把json文件加载为Python的数据格式,…...

Flink State 和 Fault Tolerance详解
有状态操作或者操作算子在处理DataStream的元素或者事件的时候需要存储计算的中间状态,这就使得状态在整个Flink的精细化计算中有着非常重要的地位: 记录数据从某一个过去时间点到当前时间的状态信息。以每分钟/小时/天汇总事件时,状态将保留…...

小红书2023“家生活”趋势白皮书
关于报告的所有内容,公众【营销人星球】获取下载查看 核心观点 近年来,年轻人与家的关系愈发紧密。 在小红书上,我们观察到了家居家装内容的蓬勃生长,3 年来相关内容的笔记规模增长了6倍,相关品类的搜索量增加的 3.…...

使用 LangChain 搭建基于 Amazon DynamoDB 的大语言模型应用
LangChain 是一个旨在简化使用大型语言模型创建应用程序的框架。作为语言模型集成框架,在这个应用场景中,LangChain 将与 Amazon DynamoDB 紧密结合,构建一个完整的基于大语言模型的聊天应用。 本次活动,我们特意邀请了亚马逊云科…...

210. 课程表 II Python
文章目录 一、题目描述示例 1示例 2示例 3 二、代码三、解题思路 一、题目描述 现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] [ai, bi] ,表示在选修课程 ai 前 必须 …...

【LeetCode 算法】Linked List Cycle II 环形链表 II
文章目录 Linked List Cycle II 环形链表 II问题描述:分析代码哈希快慢指针 Tag Linked List Cycle II 环形链表 II 问题描述: 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链…...

蒸散发与植被总初级生产力估算
目标 熟悉蒸散发ET及其组分(植被蒸腾Ec、土壤蒸发Es、冠层截留Ei)、植被总初级生产力GPP的概念和碳水耦合的基本原理;掌握利用Python与ArcGIS工具进行课程相关的操作;熟练掌握国际上流行的Penman-Monteith模型,并能够…...
uniapp微信小程序底部弹窗自定义组件
基础弹窗效果组件 <template><view><viewclass"tui-actionsheet-class tui-actionsheet":class"[show ? tui-actionsheet-show : ]"><view class"regional-selection">底部弹窗</view></view><!-- 遮罩…...

人工智能的最新进展:2024年将会发生什么?
文章目录 2024年AI最新发展2024年AI具体应用2024年AI的具体预测 ✍创作者:全栈弄潮儿 🏡 个人主页: 全栈弄潮儿的个人主页 🏙️ 个人社区,欢迎你的加入:全栈弄潮儿的个人社区 📙 专栏地址&#…...

使用Golang实现一套流程可配置,适用于广告、推荐系统的业务性框架——组合应用
在《使用Golang实现一套流程可配置,适用于广告、推荐系统的业务性框架——简单应用》中,我们看到了各种组合Handler的组件,如HandlerGroup和Layer。这些组件下面的子模块又是不同组件,比如LayerCenter的子组件是Layer。如果此时我…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

