Java进阶——数据结构与算法之哈希表与树的入门小结(四)
文章大纲
- 引言
- 一、哈希表
- 1、哈希表概述
- 2、哈希表的基本设计思想
- 3、JDK中的哈希表的设计思想概述
- 二、树
- 1、树的概述
- 2、树的特点
- 3、树的相关术语
- 4、树的存储结构
- 4.1、双亲表示法
- 4.2、孩子兄弟表示法:
- 4.3、孩子表示法:
- 4.4、双亲孩子表示法
- 三、二叉树
- 1、二叉树的性质
- 3、二叉树的类型
- 4、二叉树的存储结构
- 5、二叉树的遍历
- 5.1、先序遍历(根结点 ---> 左子树 ---> 右子树)
- 5.2、中序遍历(左子树 ---> 根结点 ---> 右子树)
- 5.3、后序遍历(左子树 ---> 右子树 ---> 根结点)
- 6、二叉树的链式实现
引言
前面介绍了线性表结构中的顺序存储结构寻址容易但是插入删除性能不好,而链式结构插入删除性能较好寻址却欠佳,那么有没有“鱼和熊掌兼可得”的结构呢?
一、哈希表
1、哈希表概述
哈希表(Hash table也叫散列表),是根据关键码值(Key value)而直接进行访问的数据结构。即它通过把关键码值映射到表中一个位置来访问记录,直接通过key来加快查找的速度,这个映射函数叫做散列函数,散列函数就是用于计算哈希值的,存放记录的数组叫做散列表。
2、哈希表的基本设计思想
以一个实例简单分析下哈希表的设计思想,首先我们有一组数据{14,19,5,7,21,1,13,0,18}需要存储,暂且设计散列表长度为预存储数组的长度,最后再设计一个映射公式即散列函数表达式f(x)= x mod 13,经过映射之后无论多大的数据都能确保经过散列函数计算之后在散列表下标范围内(当然我们用的hashCode要比这复杂得多不过核心思想是一样的)

当然以上是一种简单的哈希表基本设计思想,适用于特定的场景,比如说通讯录、QQ好友列表、微信好友列表、字典等有上限的且重复不多的数据存储。
3、JDK中的哈希表的设计思想概述
JDK中采用的是所谓的拉链法,JDK1.7之前采用的是数组+单链表的结构,而在之后改成了数组+单链表+红黑树的结构,基本思想是一致的,区别在于解决哈希冲突的方案,JDK1.7之前散列表中存储的元素上一个单链表,当发生哈希冲突时,直接把值添加到链表尾部,这样就解决了哈希冲突,但是为了避免单链表长度过长,在JDK1.8之后设置来一个阈值,当链表长度超过这个阈值时则自动转为红黑树进行存储。

二、树
1、树的概述
树是一种数据结构,它是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,不过它是根朝上,而叶朝下的,当n>0时根结点是唯一的,不可能存在多个根结点,数据结构中的树只能有一个根结点;.m>0时,子树的个数没有限制,但它们一定是互不相交的。单个结点是一棵树,树根就是该结点本身。
2、树的特点
- 每个结点有零个或多个子结点;
- 没有父结点的结点称为根结点;
- 每一个非根结点有且只有一个父结点;
- 除了根结点外,每个子结点可以分为多个不相交的子树
3、树的相关术语
- 结点的度——一个结点含有的子树的个数称为该结点的度;
- 叶结点或终端结点——度为0的结点称为叶结点;
- 非终端结点或分支结点——度不为0的结点;
- 双亲结点或父结点——若一个结点含有子结点,则这个结点称为其子结点的父结点;
- 孩子结点或子结点——一个结点含有的子树的根结点称为该结点的子结点;
- 兄弟结点——具有相同父结点的结点互称为兄弟结点;
- 树的度——一棵树中,最大的结点的度称为树的度;
- 结点的层次——从根开始定义起,根为第1层,根的子结点为第2层,以此类推;
- 树的高度或深度——树中结点的最大层次;
- 堂兄弟结点——双亲在同一层的结点互为堂兄弟;
- 结点的祖先——从根到该结点所经分支上的所有结点;
- 子孙——以某结点为根的子树中任一结点都称为该结点的子孙。
- 森林——由m(m>=0)棵互不相交的树的集合称为森林;

4、树的存储结构
树的存储结构有有四种:双亲表示法、孩子兄弟表示法、孩子表示法、双亲孩子表示法
4.1、双亲表示法
把所有节点都村存在一组连续空间中,同时在每个结点中,附设一个指示器指示其双亲结点到链表中的位置。
节点结构为
| data(数据域) | parent(指针域) |
|---|---|
| 存储结点的数据信息 | 存储该结点的双亲所在数组中的下标 |
 |
根节点的指针域为-1,根据结点的parent指针很容易找到它的双亲结点。所用时间复杂度为O(1),直到parent为-1时,表示找到了树结点的根。
4.2、孩子兄弟表示法:
任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。因此我们设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟,结点结构:
| data(数据域) | firstchild(指针域) | rightsib(指针域) |
|---|---|---|
| data是数据域 | 存储该结点的第一个孩子结点的存储地址 | 存储该结点的右兄弟结点的存储地址 |
 |
4.3、孩子表示法:
把每个结点的孩子结点排列起来,以单链表作存储结构,则n个结点有n个孩子链表,如果是叶子结点则此单链表为空,然后n个头指针又组成一个线性表,采用顺序存储结构,存放进一个一维数组中。为此设计两种结点结构:一种是孩子链表的孩子结点:
| child(数据域) | next(指针域) |
|---|---|
| 存储某个结点在表头数组中的下标 | 存储指向某结点的下一个孩子结点的指针 |
| 另一种是表头数组的表头结点: | |
| data(数据域) | firstchild(头指针域) |
| — | — |
| 存储某个结点的数据信息 | 存储该结点的孩子链表的头指针 |

4.4、双亲孩子表示法

三、二叉树
二叉树是**每个结点最多有两个子树的树结构,**通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树不是树的一种特殊情形,尽管其与树有许多相似之处,但树和二叉树有两个主要差别,树中结点的最大度数没有限制,而二叉树结点的最大度数为2, 树的结点无左、右之分,而二叉树的结点有左、右之分。
1、二叉树的性质
- 在非空二叉树中,第i层的结点总数不超过2的(i-1)次方 , i>=1
- 深度为h的二叉树最多有 2的h次方减1个结点(h>=1),最少有h个结点
- 对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1
- 具有n个结点的完全二叉树的深度为 [log2 N]+1 (注:[ ]表示向下取整)
- 有N个结点的完全二叉树各结点如果用顺序方式存储,则结点之间有如下关系:若I为结点编号则 如果I>1,则其父结点的编号为I/2;如果2I<=N,则其左孩子(即左子树的根结点)的编号为2I;若2I>N,则无左孩子;如果2I+1<=N,则其右孩子的结点编号为2I+1;若2I+1>N,则无右孩子。
- 给定N个节点,能构成h(N)种不同的二叉树。h(N)为卡特兰数的第N项。h(n)=C(2*n,n)/(n+1)。
- 设有i个枝点,I为所有枝点的道路长度总和,J为叶的道路长度总和J=I+2i [2]
3、二叉树的类型
- 完全二叉树——若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。
- 满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
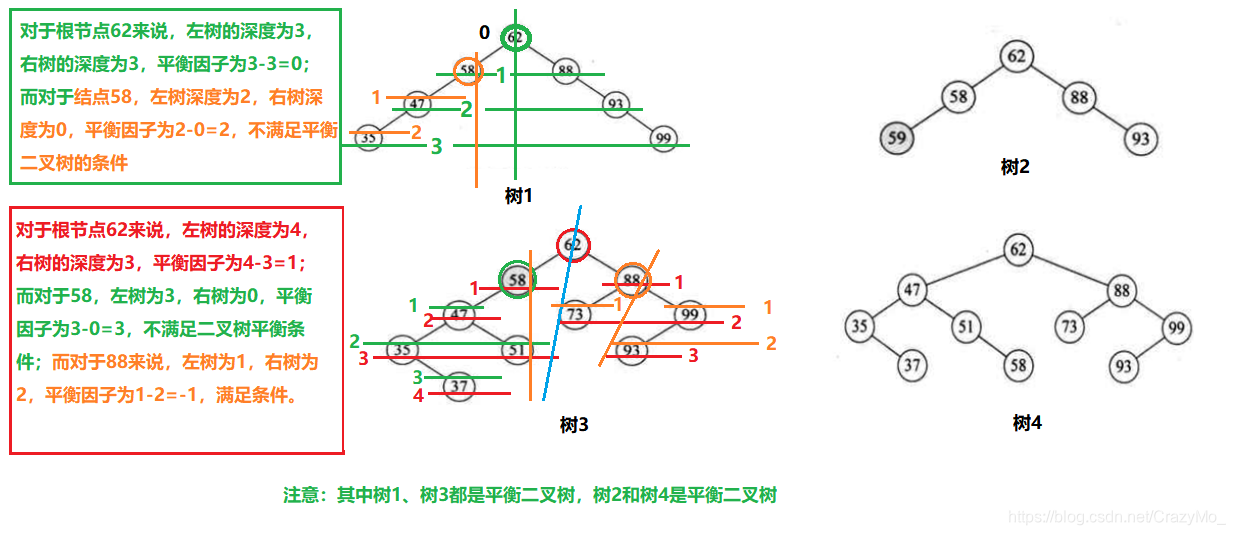
- 平衡二叉树——平衡二叉树又被称为AVL树(区别于AVL算法),它是一棵二叉排序树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
4、二叉树的存储结构

5、二叉树的遍历
遍历是对树的一种最基本的运算,所谓遍历二叉树就是按一定的规则和顺序走遍二叉树的所有结点,使每一个结点都被访问一次,而且只被访问一次。由于二叉树是非线性结构,因此,树的遍历实质上是将二叉树的各个结点转换成为一个线性序列来表示。假设L、D、R分别表示遍历左子树、访问根结点和遍历右子树, 则对一棵二叉树的遍历有三种情况:DLR(称为先根次序遍历),LDR(称为中根次序遍历),LRD (称为后根次序遍历)。

5.1、先序遍历(根结点 —> 左子树 —> 右子树)
首先访问根,再先序遍历左子树,最后先序遍历右子树。
public void postOrderTraversal(TreeNode root) {if (root != null) {return;}postOrderTraversa1(root.left);postOrderTraversa1(root.right);System.out.print(root.val+" ");
}
非递归版本
public void preOrderTraversval2(TreeNode root) {LinkedList<TreeNode> stack = new LinkedList<>();TreeNode pNode = root;while (pNode != null || !stack.isEmpty()) {if (pNode != null) {System.out.print(pNode.val+" ");stack.push(pNode);pNode = pNode.left;} else { //pNode == null && !stack.isEmpty()TreeNode node = stack.pop();pNode = node.right;}}}
5.2、中序遍历(左子树 —> 根结点 —> 右子树)
首先中序遍历左子树,再访问根,最后中序遍历右子树
public void postOrderTraversal(TreeNode root) {if (root != null) {return;}postOrderTraversa1(root.left);postOrderTraversa1(root.right);System.out.print(root.val+" ");
}
5.3、后序遍历(左子树 —> 右子树 —> 根结点)
首先后序遍历左子树,再后序遍历右子树,最后访问根,即
public void postOrderTraversal(TreeNode root) {if (root != null) {return;}postOrderTraversa1(root.left);postOrderTraversa1(root.right);System.out.print(root.val+" ");
}
6、二叉树的链式实现
package com.crazymo.ndk.tree;public class BinaryTree<E> {public TreeNode<E> root;public BinaryTree(E data){root=new TreeNode<>(data,null,null);}public void createTree(){TreeNode<String> nodeB=new TreeNode<String>("B",null,null);TreeNode<String> nodeC=new TreeNode<String>("C",null,null);TreeNode<String> nodeD=new TreeNode<String>("D",null,null);TreeNode<String> nodeE=new TreeNode<String>("E",null,null);TreeNode<String> nodeF=new TreeNode<String>("F",null,null);TreeNode<String> nodeG=new TreeNode<String>("G",null,null);TreeNode<String> nodeH=new TreeNode<String>("H",null,null);TreeNode<String> nodeJ=new TreeNode<String>("J",null,null);TreeNode<String> nodeI=new TreeNode<String>("I",null,null);root.leftChild= (TreeNode<E>) nodeB;root.rightChild= (TreeNode<E>) nodeC;nodeB.leftChild=nodeD;nodeC.leftChild=nodeE;nodeC.rightChild=nodeF;nodeD.leftChild=nodeG;nodeD.rightChild=nodeH;nodeE.rightChild=nodeJ;nodeH.leftChild=nodeI;}/*** 中序访问树的所有节点*/public void midOrderTraverse(TreeNode<E> root){//逻辑if(root==null){return;}midOrderTraverse(root.leftChild);//逻辑System.out.print("mid:"+root.data+"\t");//输出midOrderTraverse(root.rightChild);//逻辑}/*** 前序访问树的所有节点 Arrays.sort();*/public void preOrderTraverse(TreeNode<E> root){if(root==null){return;}System.out.print("pre:"+root.data+"\t");preOrderTraverse(root.leftChild);preOrderTraverse(root.rightChild);}/*** 后序访问树的所有节点*/public void postOrderTraverse(TreeNode<E> root){if(root==null){return;}postOrderTraverse(root.leftChild);postOrderTraverse(root.rightChild);System.out.print("post:"+root.data+"\t");}/***节点的数据结构* @param <E>*/public class TreeNode<E> {E data;TreeNode<E> leftChild;TreeNode<E> rightChild;public TreeNode(E data, TreeNode<E> leftChild, TreeNode<E> rightChild) {this.data = data;this.leftChild = leftChild;this.rightChild = rightChild;}}
}树的遍历
BinaryTree binarayTree=new BinaryTree("A");//构造简单二叉树binarayTree.createTree();binarayTree.midOrderTraverse(binarayTree.root);System.out.println();binarayTree.preOrderTraverse(binarayTree.root);System.out.println();binarayTree.postOrderTraverse(binarayTree.root);

相关文章:

Java进阶——数据结构与算法之哈希表与树的入门小结(四)
文章大纲 引言一、哈希表1、哈希表概述2、哈希表的基本设计思想3、JDK中的哈希表的设计思想概述 二、树1、树的概述2、树的特点3、树的相关术语4、树的存储结构4.1、双亲表示法4.2、孩子兄弟表示法:4.3、孩子表示法:4.4、双亲孩子表示法 三、二叉树1、二…...

DataFrame中按某字段分类并且取该分类随机数量的数据
最近有个需求,把某个df中的数据,按照特定字段分类,并且每个分类只取随机数量数据,这个随机数量需要有范围限制。写出来记录下。 def randomCutData(self, df, startNum):grouped df.groupby(classify_label)df_sampled pd.Data…...
【c++】rand()随机函数的应用(一)——rand()函数详解和实例
c语言中可以用rand()函数生成随机数,今天来探讨一下rand()函数的基本用法和实际应用。 本系列文章共分两讲,今天主要介绍一下伪随机数生成的原理,以及在伪随机数生成的基础上,生成随机数的技巧,下一讲主要介绍无重复随…...
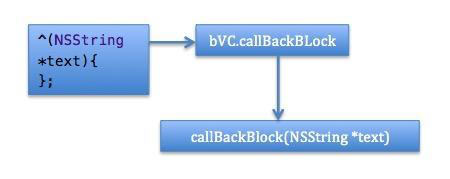
iOS——Block回调
先跟着我实现最简单的 Block 回调传参的使用,如果你能举一反三,基本上可以满足了 OC 中的开发需求。已经实现的同学可以跳到下一节。 首先解释一下我们例子要实现什么功能(其实是烂大街又最形象的例子): 有两个视图控…...
)
html学习6(xhtml)
1、xhtml是以xml格式编写的html。 2、xhtml与html的文档结构区别: DOCTYPE是强制性的<html>、<head>、<title>、<body>也是强制性的<html>中xmlns属性是强制性的 3、 元素语法区别: xhtml元素必须正确嵌套xhtml元素必…...
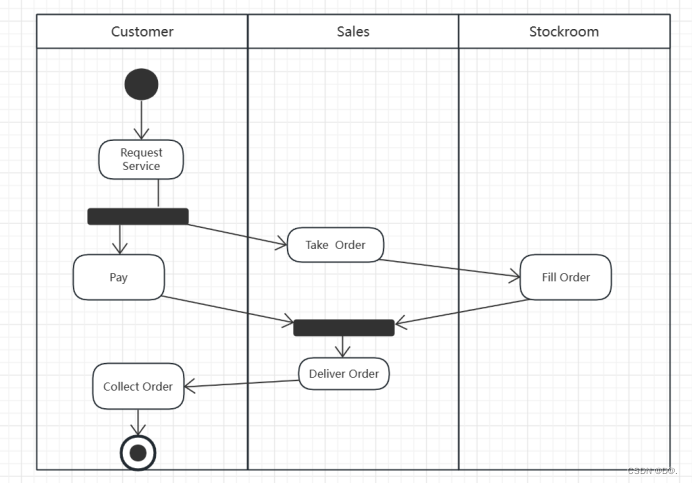
UML-活动图
目录 一.活动图概述: 1.活动图的作用: 2.以下场合不使用活动图: 3.活动图的基本要素: 4.活动图的图符 4.1起始状态 4.2终止状态 4.3状态迁移 4.4决策点 4.5同步条:表示活动之间的不同 5.活动图: 二.泳道: 1.泳道图&a…...

跨境电商怎么做?Live Market教你创业及做大生意
随着全球化的不断深入和互联网技术的迅猛发展,跨境电商成为了一个蓬勃发展的行业。根据eMarketer的数据,2021年全球跨境电商销售额将达到4.5万亿美元,预计到2025年将增长至6.3万亿美元。这表明,跨境电商行业将继续保持强劲增长的趋…...

Linux 4.19 和Linux 5.10 的区别
Linux 4.19和Linux 5.10是Linux内核的两个不同版本。它们之间有一些重要的区别,包括功能、性能和支持方面的改进。以下是一些常见的区别: 功能增强:Linux 5.10相对于4.19引入了许多新功能和增强。例如,Linux 5.10引入了BPF&#x…...
学习单片机的秘诀:实践与坚持
在学习单片机时,将实践与学习结合起来是一个很好的方法。不要一上来就死磕指令和名词,而是边学边做实验,循序渐进地理解和应用指令。通过实验,你能亲身感受到指令的控制效果,增强对单片机的理解和兴趣。 学习单片机不…...
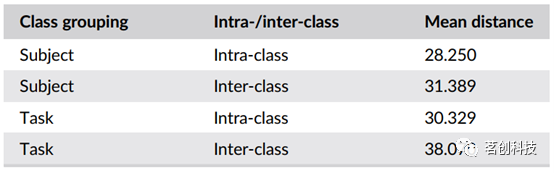
Hum Brain Mapp:用于功能连接体指纹识别和认知状态解码的高精度机器学习技术
摘要 人脑是一个复杂的网络,由功能和解剖上相互连接的脑区组成。越来越多的研究表明,对脑网络的实证估计可能有助于发现疾病和认知状态的生物标志物。然而,实现这一目标的先决条件是脑网络还必须是个体的可靠标记。在这里,本研究…...

Ajax图书管理业务
图书管理业务 Ajax图书管理业务 需求: 对服务器的图书数据进行 增、删、改、查。功能的实现,同时实时动态的渲染刷新页面内容 根据功能模块分为四个业务模块,下面有各个业务的实现步骤 01_ 渲染图书列表业务 * 目标1:渲染图书列表 * 1.1 获…...

对于爬虫代码的优化,多个方向
对于优化爬虫,有许多可能的方法,这取决于你的具体需求和目标。以下是一些常见的优化策略: 1. **并发请求**:你可以使用多线程或异步IO来同时发送多个请求,这可以显著提高爬虫的速度。Python的concurrent.futures库或a…...

ffmpeg推流卡顿修复
1、使用命令如下: $"ffmpeg -i {this.IpAddress} -f flv {PushAddress}" 2、参考文章: ffmpeg 编码如何做带宽控制输出_ffmpeg bufsize_qianbo_insist的博客-CSDN博客...
Java02-迭代器,数据结构,List,Set ,TreeSet集合,Collections工具类
目录 什么是遍历? 一、Collection集合的遍历方式 1.迭代器遍历 方法 流程 案例 2. foreach(增强for循环)遍历 案例 3.Lamdba表达式遍历 案例 二、数据结构 数据结构介绍 常见数据结构 栈(Stack) 队列&a…...
离散 Hopfield 神经网络的分类与matlab实现
1 案例背景 1.1离散 Hopfield 神经网络学习规则 离散型 Hopfield神经网络的结构、工作方式,稳定性等问题在第9章中已经进行了详细的介绍,此处不再赘述。本节将详细介绍离散Hopfield神经网络权系数矩阵的设计方法。设计权系数矩阵的目的是: ①保证系统在异步工作时的稳…...
opencv 30 -图像平滑处理01-均值滤波 cv2.blur()
什么是图像平滑处理? 图像平滑处理(Image Smoothing)是一种图像处理技术,旨在减少图像中的噪声、去除细节并平滑图像的过渡部分。这种处理常用于预处理图像,以便在后续图像处理任务中获得更好的结果。 常用的图像平滑处理方法包括…...

中小企业的数字化营销应该如何着手?数字化营销到底要怎么做?
从侠义角度讲,数字化营销就是在数字化的媒体上做营销。传播本质上是一种营销的形式 从广义角度讲,我们不仅可以将营销数字化,也可以数字化很多事物,甚至行业,比如数字化制造业、数字化工厂、数字化商会等等 而这个…...
实数信号的傅里叶级数研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

oracle数据库巡检脚本
用于Oracle数据库巡检的示例脚本: #!/bin/bash# 设置数据库连接信息 DB_USER="your_db_username" DB_PASSWORD="your_db_password" DB_HOST="your_db_host" DB_PORT="your_db_port" DB_SID="your_db_sid" OUTPUT_FILE=&q…...
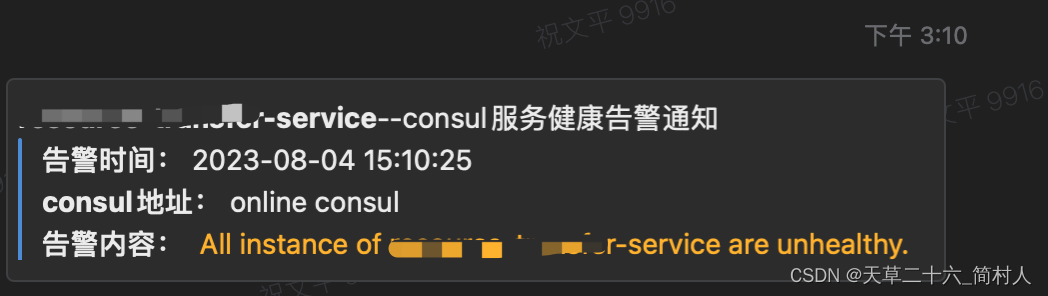
服务注册中心consul的服务健康监控及告警
一、背景 consul既可以作为服务注册中心,也可以作为分布式配置中心。当它作为服务注册中心的时候,java微服务之间的调用,会定期查询服务的实例列表,并且实例的状态是健康可用。 如果发现被调用的服务,注册到consul的…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
