2023牛客暑期多校训练营6 A-Tree (kruskal重构树))
文章目录
- 题目大意
- 题解
- 参考代码
题目大意

( 0 ≤ a i ≤ 1 ) , ( 1 ≤ c o s t i ≤ 1 0 9 ) (0\leq a_i\leq 1),(1 \leq cost_i\leq 10^9) (0≤ai≤1),(1≤costi≤109)
题解
提供一种新的算法,kruskal重构树。
该算法重新构树,按边权排序每一条边后,
新建一个点为“两边的节点所在最大节点”的父节点,该点点权为该边边权。
该树有一些特征:
①:是一个二叉树。
③:原节点全部为叶节点。
②:两个节点的LCA的点权就是其原最短路径的最大边权。
具体 Kruskal 算法学习
建树可以用并查集计算。
了解了这个算法我们再看问题,要求最大边权,这点可以用kruskal维护。
对于某个不为叶节点的节点 x x x ,它左儿子与右儿子匹配的黑白节点的最大边权显然为 w x w_x wx 。
显然的,我们可以枚举左右儿子节点中的黑白节点个数,乘上点权,即为该点的贡献。
我们发现答案可以通过 d f s dfs dfs 顺序从下往上来求解,且不会造成前效性,所以树形DP可以很好的解决这道题。
设 d p x , b dp_{x,b} dpx,b 表示在 x x x 的子树内有 b b b 个黑色节点的最优解。
d p x , b = m a x ( d p s o n , b l a c k 1 + d p s o n , b 2 + w x ∗ ( b l a c k 1 ∗ w h i t e 2 + b l a c k 2 ∗ w h i t e 1 ) ) dp_{x,b}=max(dp_{son,black1}+dp_{son,b2}+w_x*(black1*white2+black2*white1)) dpx,b=max(dpson,black1+dpson,b2+wx∗(black1∗white2+black2∗white1))
white/black_1/2表示1/2的子树中有几个白色/黑色节点
且black1+black2=b
我们发现枚举 b b b 的黑白分布情况,最多需要合并 m i n ( s u m s o n l , s u m s o n r ) min(sum_{sonl},sum_{sonr}) min(sumsonl,sumsonr)次,
不然的话就需要从大的部分取一部分给数量少的一颗子树。
特殊的,对于叶节点
d p x , b = ( w x = = b ˆ 1 ) ∗ − c o s t x dp_{x,b}=(w_x==b \^\ 1)*-cost_x dpx,b=(wx==b ˆ1)∗−costx
剩下的就好处理多了,写个DFS遍历一下即可处理。
计算时间复杂度,对于kruskal重构树,合并时长度最大为 l o g n log_n logn
即时间复杂度为 O ( N 2 l o g N ) O(N^2log_N) O(N2logN) 可以通过。
参考代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=6e3+5;
const int inf=1e18+7;
struct node{int x,y,w;
}f[N];
int fa[N],cost[N];
int w[N];
int n,m,t,ans;
int sonl[N],sonr[N];
int sum[N];
int dp[N][3000];
void dfs(int x)
{if(x<=n) //叶节点{dp[x][0]=(w[x]==1)*(-cost[x]);dp[x][1]=(w[x]==0)*(-cost[x]);
// cout<<x<<" "<<0<<" "<<dp[x][0]<<endl;
// cout<<x<<" "<<1<<" "<<dp[x][1]<<endl;sum[x]=1;}else{dfs(sonl[x]);dfs(sonr[x]);int res=min(sum[sonl[x]],sum[sonr[x]]); //启发式合并平均复杂度为log_nsum[x]=sum[sonl[x]]+sum[sonr[x]];for(int i=0;i<=sum[sonl[x]];i++)for(int j=0;j<=sum[sonr[x]];j++)dp[x][i+j]=-inf;for(int i=0;i<=sum[sonl[x]];i++) //枚举黑色节点个数{for(int j=0;j<=sum[sonr[x]];j++) //DP转移{int s=dp[sonl[x]][i]+dp[sonr[x]][j]+w[x]*(i*(sum[sonr[x]]-j)+(sum[sonl[x]]-i)*j);dp[x][i+j]=max(dp[x][i+j],s);ans=max(ans,dp[x][i+j]);}} }
}
int cmp(node a,node b)
{return a.w<b.w;
}
int sf(int x)
{if(fa[x]==x)return x;return fa[x]=sf(fa[x]);
}
signed main()
{cin>>n;for(int i=1;i<=n;i++)scanf("%lld",&w[i]);for(int i=1;i<=n;i++)scanf("%lld",&cost[i]);for(int i=1;i<n;i++)scanf("%lld%lld%lld",&f[i].x,&f[i].y,&f[i].w);sort(f+1,f+n,cmp);t=n;for(int i=1;i<=2*n;i++)fa[i]=i;for(int i=1;i<n;i++) //kruskal构树{int x=sf(f[i].x),y=sf(f[i].y);fa[x]=++t;fa[y]=t;w[t]=f[i].w;sonl[t]=x;sonr[t]=y;}dfs(t);printf("%lld",ans);
}
相关文章:

2023牛客暑期多校训练营6 A-Tree (kruskal重构树))
文章目录 题目大意题解参考代码 题目大意 ( 0 ≤ a i ≤ 1 ) , ( 1 ≤ c o s t i ≤ 1 0 9 ) (0\leq a_i\leq 1),(1 \leq cost_i\leq 10^9) (0≤ai≤1),(1≤costi≤109) 题解 提供一种新的算法,kruskal重构树。 该算法重新构树,按边权排序每一条边…...
软件测试—支付功能测试
有人问过我这样一个问题:作为一个支付平台,接入了快钱、易宝或直连银行等多家的渠道,内在的产品流程是自己的。业内有什么比较好的测试办法,来测试各渠道及其支持的银行通道呢? 回答:对支付平台而言&#…...

自动化测试的统筹规划
背景 回顾以前自动化测试编写的经历,主要是以开发者自驱动的方式进行,测试的编写随心而动,没有规划,也没有章法,这样就面临如下的一些问题: 测试用例设计不到位,覆盖不全,或者不够…...
、django中如何开启事务)
外键字段的增删改查、多表查询(子查询和连表查询、正反向、聚合查询、 分组查询、 F与Q查询)、django中如何开启事务
一、 外键字段的增删改查 1.多对多的外键增删改查图书和作者是多对多,借助于第三张表实现的,如果想绑定图书和作者的关系,本质上就是在操作第三方表2.如何操作第三张表问题:让你给图书添加一个作者,他俩的关系可是多对…...
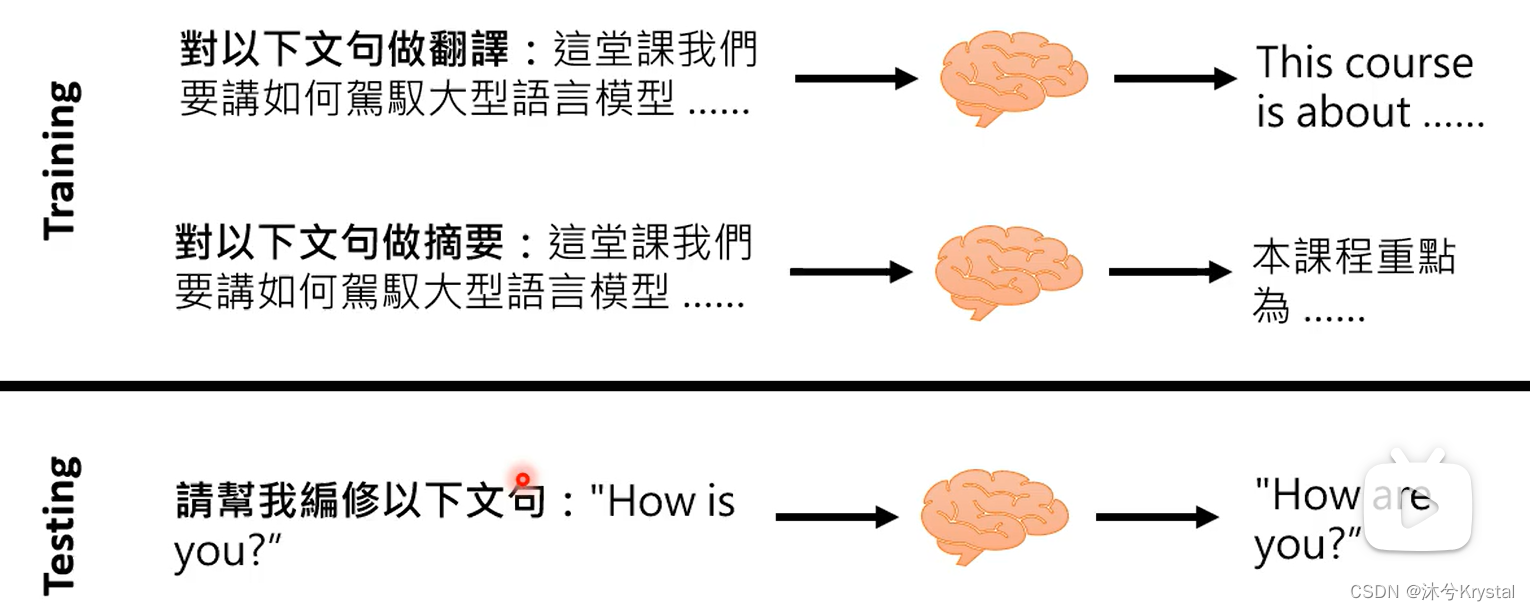
【学习笔记】生成式AI(ChatGPT原理,大型语言模型)
ChatGPT原理剖析 语言模型 文字接龙 ChatGPT在测试阶段是不联网的。 ChatGPT背后的关键技术:预训练(Pre-train) 又叫自监督式学习(Self-supervised Learning),得到的模型叫做基石模型(Founda…...

【Opencv入门到项目实战】(三):图像腐蚀与膨胀操作
文章目录 1.腐蚀操作2.膨胀操作3.开运算和闭运算4.礼帽与黑帽5.梯度运算 1.腐蚀操作 腐蚀操作是图像处理中常用的一种形态学操作,我们通常用于去除图像中的噪声、分割连通区域、减小目标物体的尺寸等。腐蚀操作的原理是,在给定的结构元素下,…...
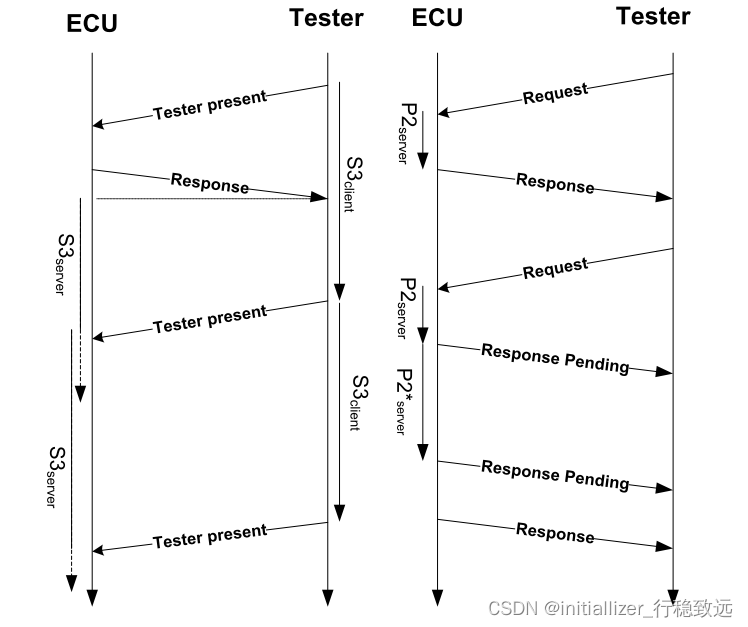
Autosar诊断系列介绍20 - UDS应用层P2Server/P2Client等时间参数解析
本文框架 1. 前言2.几个时间参数含义2.1 P2Client与P2Server2.2 P2*Client与P2*Server2.3 P3Client_Phys与P3Client_Func2.4 S3Client与S3Server 1. 前言 本系列Autosar 诊断入门介绍,会详细介绍诊断相关基础知识,如您对诊断实战有更高需求,…...
【iOS】json数据解析以及简单的网络数据请求
文章目录 前言一、json数据解析二、简单的网络数据请求三、实现访问API得到网络数据总结 前言 近期写完了暑假最后一个任务——天气预报,在里面用到了简单的网络数据请求以及json数据的解析,特此记录博客总结 一、json数据解析 JSON是一种轻量级的数据…...
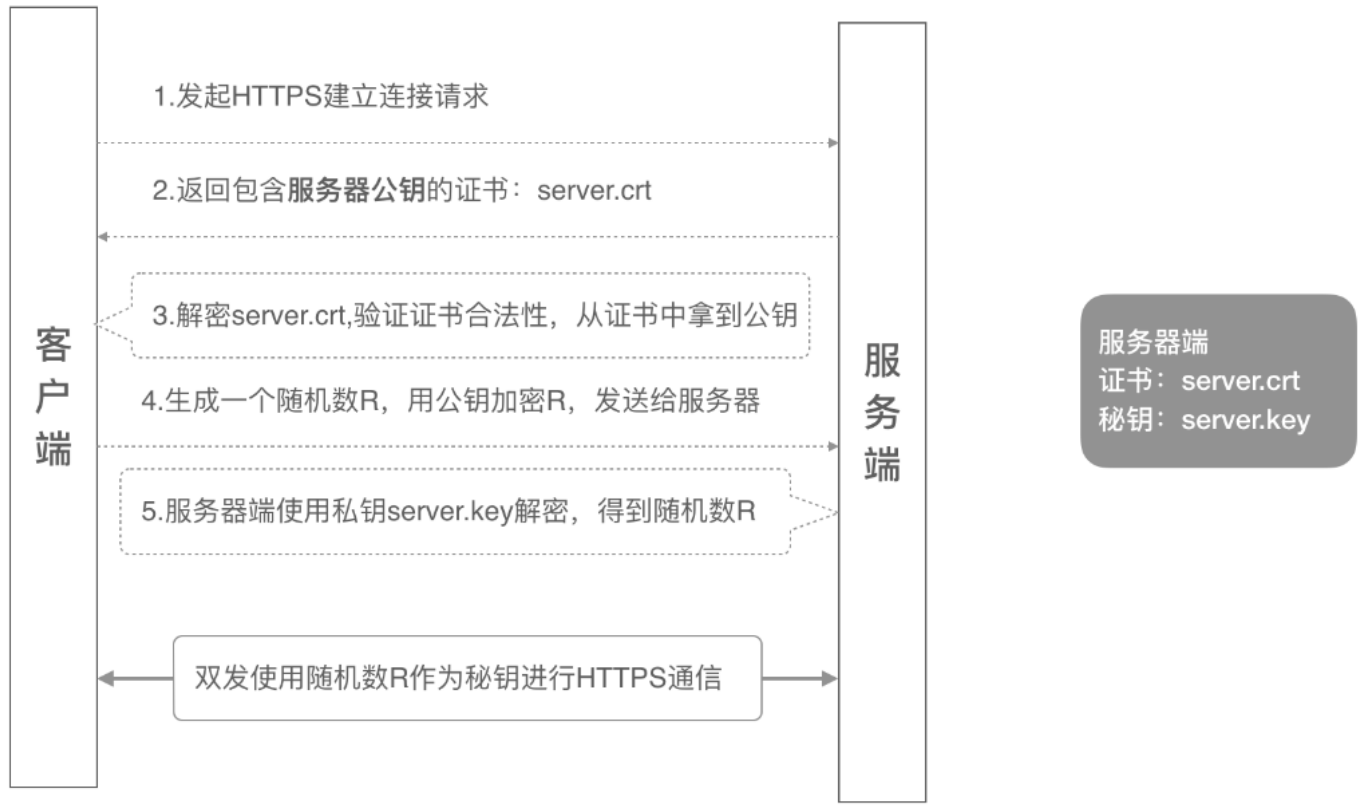
Kubernetes客户端认证—— 基于ServiceAccount的JWTToken认证
1、概述 在 Kubernetes 官方手册中给出了 “用户” 的概念,Kubernetes 集群中存在的用户包括 “普通用户” 与 “ServiceAccount”, 但是 Kubernetes 没有普通用户的管理方式,通常只是将使用集群根证书签署的有效证书的用户都被视为合法用户。…...
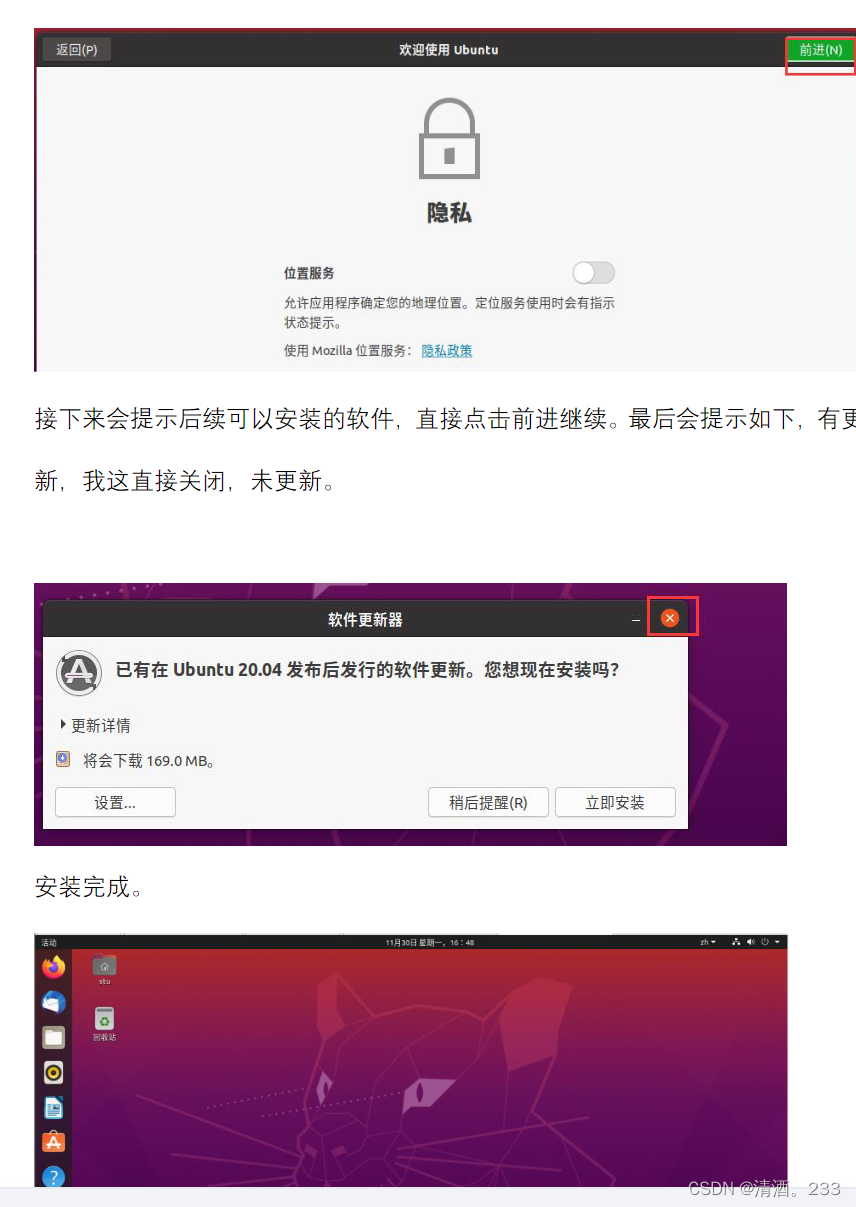
45.ubuntu Linux系统安装教程
目录 一、安装Vmware 二、Linux系统的安装 今天开始了新的学习,Linux,下面是今天学习的内容。 一、安装Vmware 这里是在 Vmware 虚拟机中安装 linux 系统,所以需要先安装 vmware 软件,然 后再安装 Linux 系统。 所需安装文件:…...

Jmeter函数助手(一)随机字符串(RandomString)
一、目标 实现一个请求单次调用,请求体里多个集合中的相同参数(zxqs)值随机从序列{01、02、03、03、04、05、06、07、08}中取 若使用CSV数据文件、用户参数等参数化手段,单次执行请求,请求体里多个集合中的相同参数&a…...

SpringCloud之微服务API网关Gateway介绍
文章目录 1 微服务API网关Gateway1.1 网关简介1.2 Spring Cloud Gateway介绍1.3 Gateway特性1.4 Gateway核心概念1.4.1 路由1.4.1.1 定义1.4.1.2 动态路由 1.4.2 断言1.4.2.1 默认断言1.4.2.2 自定义Predicate 1.4.3 过滤器1.4.3.1 默认过滤器1.4.3.2 自定义Filter(…...

机器学习入门之 pandas
pandas 有三种数据结构 一种是 Series 一种是 Dataframe import pandas as pd import numpy as np score np.random.randint(0,100,[10,5])score[0,0] 100Datascore pd.DataFrame(score)subject ["语文","数学","英语","物理&quo…...
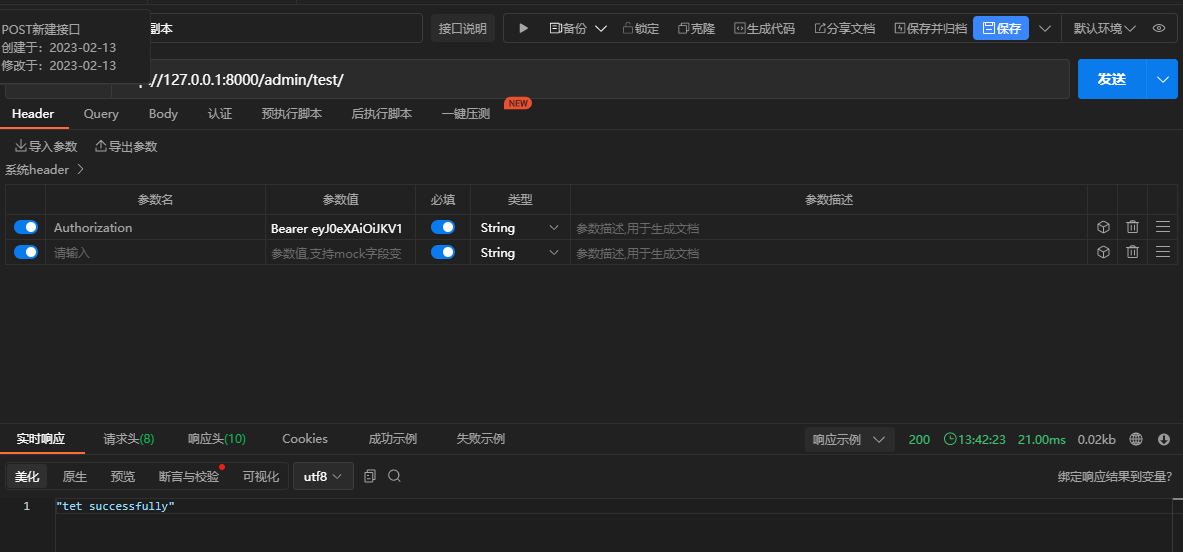
Django之JWT库与SimpleJWT库的使用
Django之JWT库与SimpleJWT库的使用 JWTJWT概述头部(header)载荷(payload)签名(signature) Django使用JWT说明jwt库的使用安装依赖库配置settings.py文件配置urls.py文件创建视图配置权限 SimpleJWT库的使用安装SimpleJWT库配置Django项目配置路由创建用户接口测试身份认证自定义…...
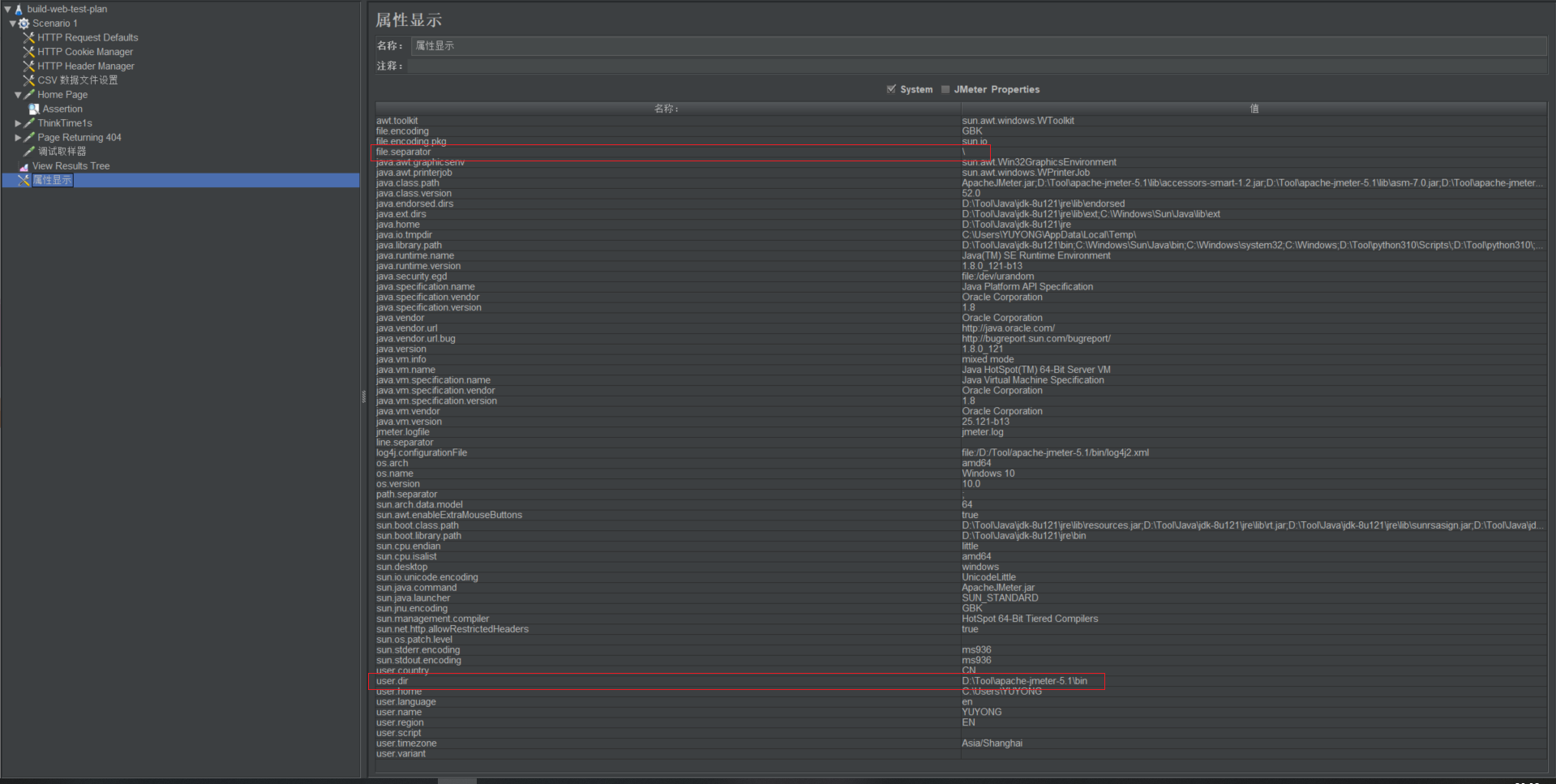
Jmeter远程服务模式运行时引用csv文件的路径配置
问题 在使用jmeter过程中,本机的内存等配置不足,启动较多的线程时,可以采用分布式运行。 在分布式运行的时候,jmeter会自动将脚本从master主机发送到remote主机上,所以不需要考虑将脚本拷贝到remote主机。但是jmeter…...

《OWASP代码审计》学习——注入漏洞审计
一、注入的概念 注入攻击允许恶意用户向应用程序添加或注入内容和命令,以修改其行为。这些类型的攻击是常见且广泛的,黑客很容易测试网站是否易受攻击,攻击者也很容易利用这些攻击。如今,它们在尚未更新的遗留应用程序中非常常见…...
Linux虚拟机中安装MySQL5.6.34
目录 第一章、xshell工具和xftp的使用1.1)xshell下载与安装1.2)xshell连接1.3)xftp下载安装和连接 第二章、安装MySQL5.6.34(不同版本安装方式不同)2.1)关闭防火墙,传输MySQL压缩包到Linux虚拟机2.2&#x…...
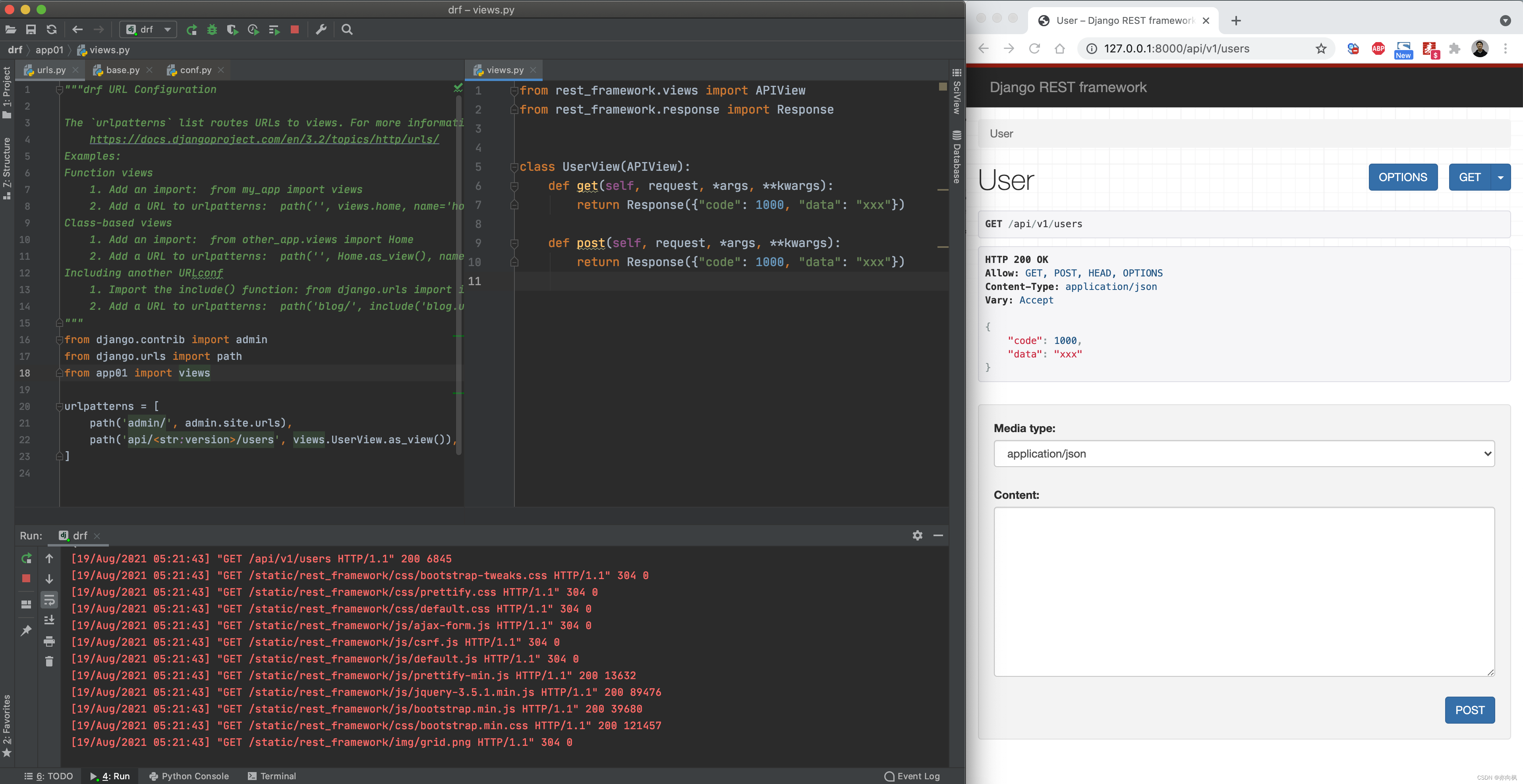
Django的FBV和CBV
Django的FBV和CBV 基于django开发项目时,对于视图可以使用 FBV 和 CBV 两种模式编写。 FBV,function base views,其实就是编写函数来处理业务请求。 from django.contrib import admin from django.urls import path from app01 import view…...

[每周一更]-(第57期):用Docker、Docker-compose部署一个完整的前后端go+vue分离项目
文章目录 1.参考项目2.技能点3.GO的Dockerfile配置后端的结构如图Dockerfile先手动docker调试服务是否可以启动报错 4.Vue的Dockerfile配置前端的结构如图nginx_docker.confDockerfile构建 5.docker-compose 整合前后端docker-compose.yml错误记录(1)ip端…...
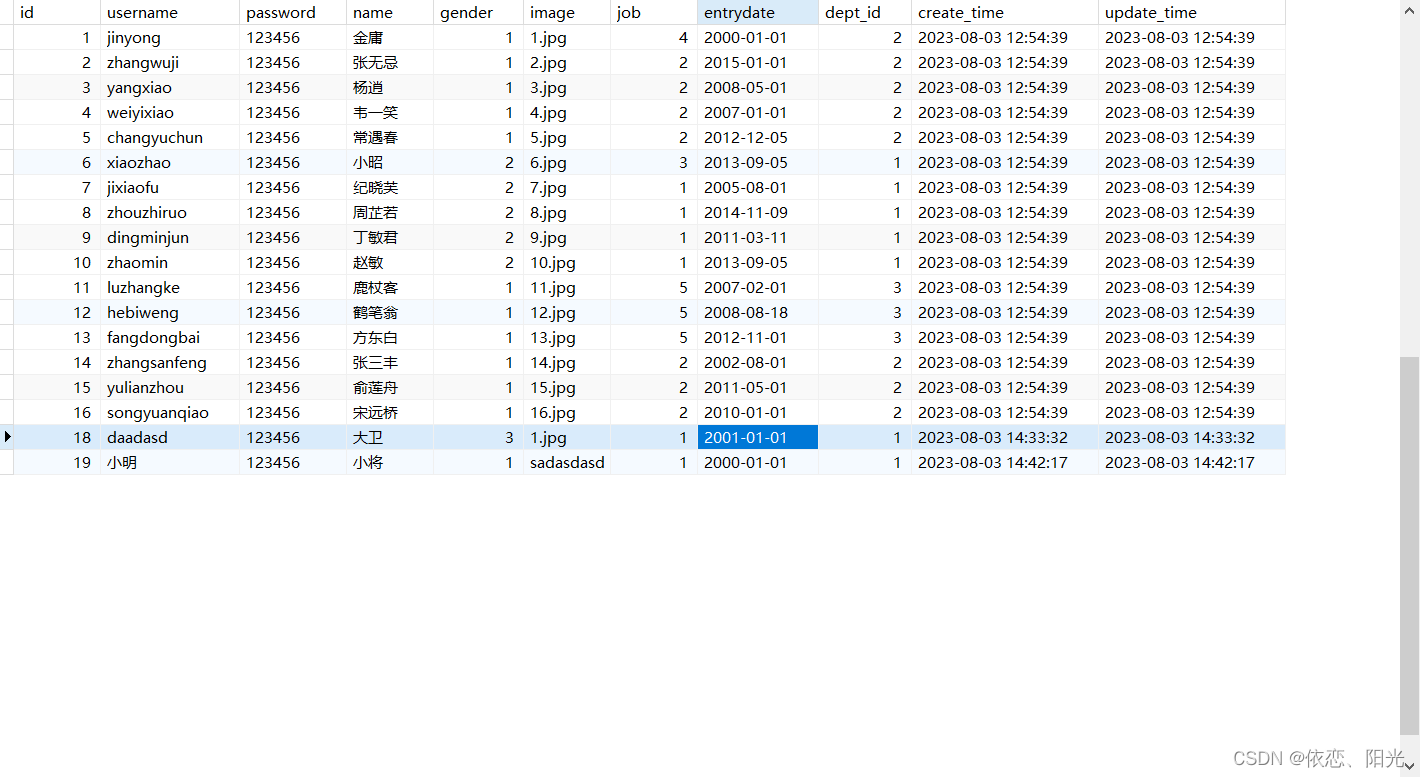
springboot-mybatis的增删改查
目录 一、准备工作 二、常用配置 三、尝试 四、增删改查 1、增加 2、删除 3、修改 4、查询 五、XML的映射方法 一、准备工作 实施前的准备工作: 准备数据库表 创建一个新的springboot工程,选择引入对应的起步依赖(mybatis、mysql驱动…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
