【LeetCode】516. 最长回文子序列
文章目录
- 1. 思路讲解
- 1.1 创建dp表
- 1.2 状态转移方程
- 1.3 不需考虑边界问题
- 2. 整体代码
1. 思路讲解
1.1 创建dp表
此题采用动态规划的方法,创建一个二维dp表,dp[i][j]表示s[i, j]中最大回文子序列的长度。且我们人为规定 i 是一定小于等于 j 的。
1.2 状态转移方程
在求dp[i][j]时,首先要判断s[i]和s[j]是否相同。
如果 s[i] == s[j]
- 如果 i == j,说明 i 与 j 的位置相同,此时dp[i][j] 就为 1
- 如果 i + 1 == j,说明 i 与 j 相邻,此时dp[i][j] 就为2
- 其他情况下,说明 i 和 j 中间有其他元素,那么此时dp[i][j] = dp[i+1][j-1] + 2;
如果s[i] != s[j]
那么此时,说明不能同时以 i 为开头和以 j 为结尾,我们去掉这种情况寻找一个最大子序列即可。方法就是在 dp[i+1, j] 和 dp[i, j-1] 中选一个最大的即可。即dp[i][j] = max(dp[i+1[j], dp[i][j-1]);
1.3 不需考虑边界问题
在求dp[i][j]的时候,我们可能会用到 i + 1 和 j - 1,在它们有可能越界的时候,一定是 i 等于 j 的时候。我们创建的dp表是二维的,我们可以想到,在可能越界的时候,就是左上角的位置或者右下角的位置,但其实这两个位置满足 i == j,那么dp[i][j] 就会被直接赋值为1,此时就不会用到 i + 1 和 j - 1 了,所以其实我们不用考虑越界的情况。
2. 整体代码
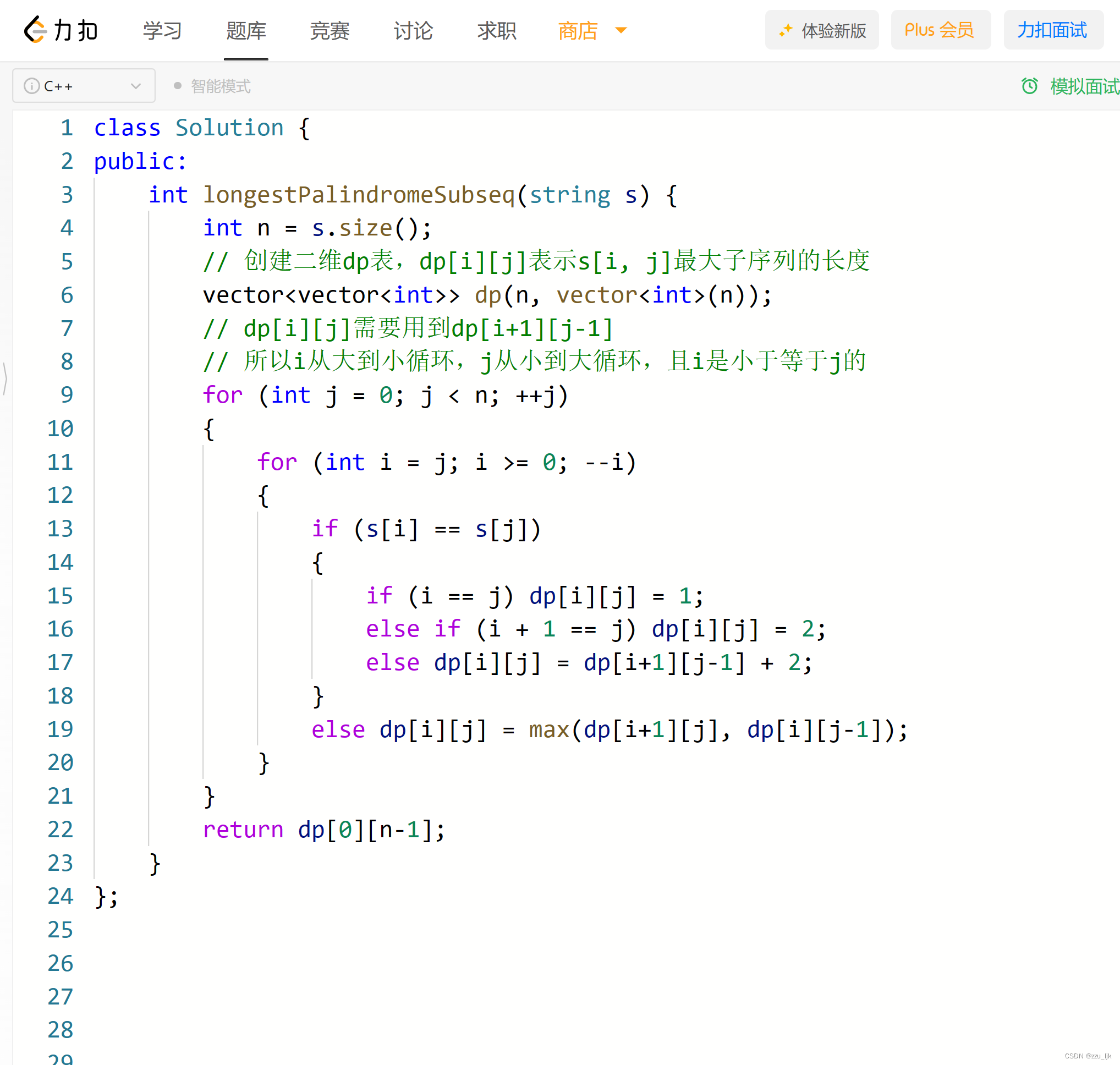
class Solution {
public:int longestPalindromeSubseq(string s) {int n = s.size();// 创建二维dp表,dp[i][j]表示s[i, j]最大子序列的长度vector<vector<int>> dp(n, vector<int>(n));// dp[i][j]需要用到dp[i+1][j-1]// 所以i从大到小循环,j从小到大循环,且i是小于等于j的for (int j = 0; j < n; ++j){for (int i = j; i >= 0; --i){if (s[i] == s[j]){if (i == j) dp[i][j] = 1;else if (i + 1 == j) dp[i][j] = 2;else dp[i][j] = dp[i+1][j-1] + 2;}else dp[i][j] = max(dp[i+1][j], dp[i][j-1]);}}return dp[0][n-1];}
};
相关文章:

【LeetCode】516. 最长回文子序列
文章目录 1. 思路讲解1.1 创建dp表1.2 状态转移方程1.3 不需考虑边界问题 2. 整体代码 1. 思路讲解 1.1 创建dp表 此题采用动态规划的方法,创建一个二维dp表,dp[i][j]表示s[i, j]中最大回文子序列的长度。且我们人为规定 i 是一定小于等于 j 的。 1.2…...
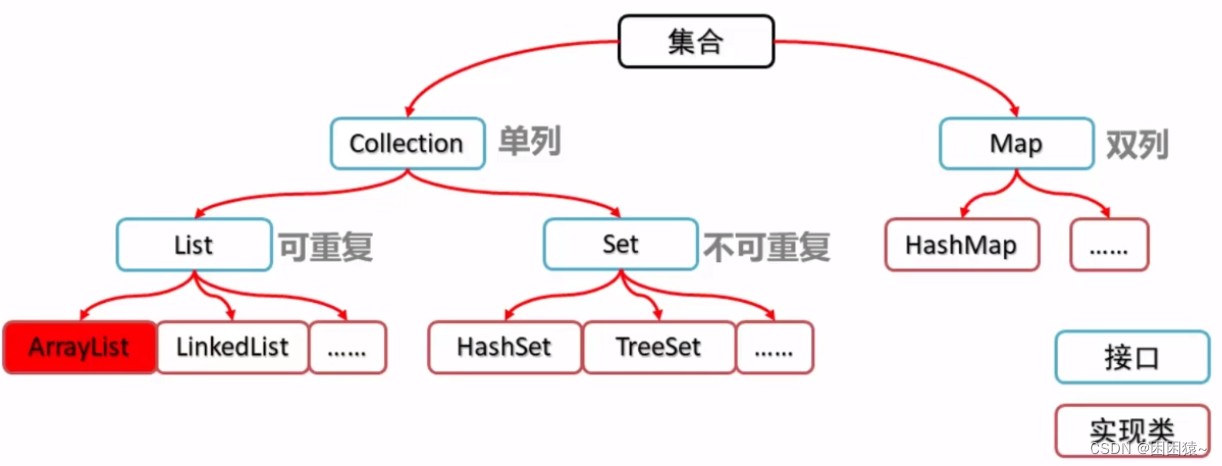
Java 集合框架
Java 集合框架提供了一组接口和类,以实现各种数据结构和算法。 集合框架满足以下几个要求。 该框架必须是高性能的。基本集合(动态数组,链表,树,哈希表)的实现也必须是高效的。 该框架允许不同类型的集合…...
遇到多人协作,我们该用git如何应对?(版本二)
一、多人协作二 1.1多人协作 一般情况下,如果有多需求需要多人同时进行开发,是不会在一个分支上进行多人开发,而是一个需求或一个功能点就要创建一个feature 分支。 现在同时有两个需求需要你和你的小伙伴进行开发,那么你们俩便…...

Flutter iOS 集成使用 fluter boost
在 Flutter项目中集成完 flutter boost,并且已经使用了 flutter boost进行了路由管理,这时如果需要和iOS混合开发,这时就要到 原生端进行集成。 注意:之前建的项目必须是 Flutter module项目,并且原生项目和flutter m…...

node.js相关的npm包的集合
一、实用功能 1. qs 一个简单易用的字符串解析和格式化库 2.rxjs RxJS是一组模块化的库,用于使用 JavaScript 中的可观察集合和组合来组合异步和基于事件的程序。 3. mitt 微型 200b 功能事件发射器/发布订阅. 4.Underscore.js Underscore.js是一个用于 JavaScript…...

Android Ble蓝牙App(二)连接与发现服务
Ble蓝牙App(二)连接与发现服务 前言正文一、GATT回调二、连接和断连三、连接状态回调四、发现服务五、服务适配器六、显示服务七、源码 前言 在上一篇中我们进行扫描设备的处理,本文中进行连接和发现服务的数据处理,运行效果图如下…...

Android 自定义按钮(可滑动、点击)
按钮图片素材 https://download.csdn.net/download/Lan_Se_Tian_Ma/88151085 px 和 dp 转换工具类(Java) // px 和 dp 转换工具类 public class DensityUtil {/*** 根据手机的分辨率从 dip 的单位 转成为 px(像素)*/public static int dip2px(Conte…...
mac录屏怎么打开?很简单,让我来教你!
mac电脑作为一款广受欢迎的电脑系统,提供了多种方式来满足用户录屏的需求。无论您是要录制教学视频、制作演示文稿,还是记录游戏精彩瞬间,mac电脑都能帮助您实现这些目标。本文将为您介绍两种mac录屏的方法。通过本文的指导,您将能…...
Stable Diffusion AI绘画学习指南【插件安装设置】
插件安装的方式 可用列表方式安装,点开Extensions 选项卡,找到如下图,找到Available选项卡,点load from加载可用插件,在可用插件列表中找到要装的插件按install 按扭按装,安装完后(Apply and restart UI)应…...

APP开发中的性能优化:提升用户满意度的关键
APP开发中的性能优化是需要持续进行的,它不仅能够让用户体验到 APP的使用感受,还能在一定程度上提升用户的满意度,从而提升 APP的粘性和转化率。不过在实际开发中,很多 APP开发公司会存在性能优化上的问题,这就需要了解…...

Golang 切片 常用方法
文章目录 移除指定位置的元素查找元素的位置查找最大最小的元素去重随机打乱排序二维排序sort.Sort 排序 下面的方法省略一些校验,如数组越界等,且都采用泛型(要求go版本 > 1.18) 移除指定位置的元素 package mainimport ("fmt" )func Del…...

【Linux后端服务器开发】poll/epoll多路转接IO服务器
目录 一、poll原理 二、poll实现多路转接IO服务器 三、epoll函数接口 四、epoll的工作原理 五、epoll实现多路转接IO服务器 一、poll原理 poll函数接口 #include <poll.h> int poll(struct pollfd *fds, nfds_t nfds, int timeout);// pollfd结构 struct pollfd …...

【设计模式——学习笔记】23种设计模式——命令模式Command(原理讲解+应用场景介绍+案例介绍+Java代码实现)
文章目录 案例引入介绍基础介绍登场角色 案例实现案例一实现 案例二介绍实现拓展 命令模式在JdbcTemplate源码中的应用总结文章说明 案例引入 有一套智能家电,其中有照明灯、风扇、冰箱、洗衣机,这些智能家电来自不同的厂家,我们不想针对每一…...

Rust中的高吞吐量流处理
本篇文章主要介绍了Rust中流处理的概念、方法和优化。作者不仅介绍了流处理的基本概念以及Rust中常用的流处理库,还使用这些库实现了一个流处理程序。 最后,作者介绍了如何通过测量空闲和阻塞时间来优化流处理程序的性能,并将这些内容同步至…...

探索编程世界的宝藏:程序员必掌握的20大算法
文章目录 1 引言2 冒泡排序算法:编程世界的排序魔法 🧙♀️🔢3 选择排序算法:排序世界的精确挑选器 🎯🔢4 插入排序算法:排序世界的巧妙插珠者 ✨🔢5 快速排序算法:排序…...

Android NFC通信示例
前言 近距离无线通信 (NFC) 是一组近距离无线技术,通常只有在距离不超过 4 厘米时才能启动连接。借助 NFC,您可以在 NFC 标签与 Android 设备之间或者两台 Android 设备之间共享小型负载。 支持 NFC 的 Android 设备同时支持以下三种主要操作模式&…...

2023年08月IDE流行度最新排名
点击查看最新IDE流行度最新排名(每月更新) 2023年08月IDE流行度最新排名 顶级IDE排名是通过分析在谷歌上搜索IDE下载页面的频率而创建的 一个IDE被搜索的次数越多,这个IDE就被认为越受欢迎。原始数据来自谷歌Trends 如果您相信集体智慧&am…...
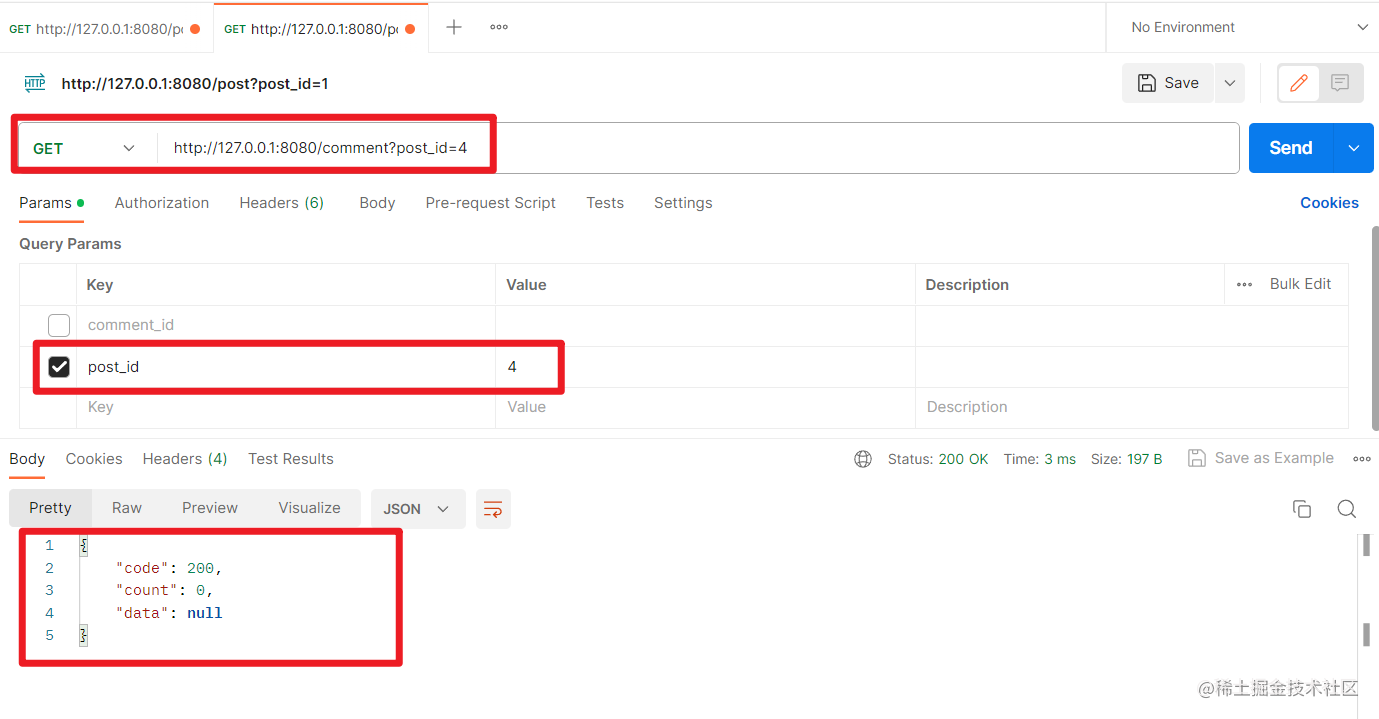
使用Beego和MySQL实现帖子和评论的应用,并进行接口测试(附源码和代码深度剖析)
文章目录 小项目介绍源码分析main.gorouter.gomodels/user.gomodels/Post.gomodels/comment.gocontrollers/post.gocontrollers/comment.go 接口测试测试增加帖子测试查看帖子测试增加评论测试查看评论 小项目介绍 经过对需求的分析,我增加了一些额外的东西&#x…...
物联网潜在的巨大价值在于大数据分析
物联网潜在的巨大价值在于大数据分析 从数据里去挖掘市场或者用户的精准需求。 往小的说,后台可以统计用户家里各各插座一年甚至更久的用电情况,这些数据也可以通过app或者小程序展现给用户。 用户可以很直观看到自己一年的用电情况,哪个家…...
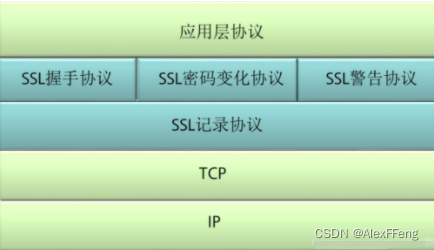
SSL原理详解
SSL协议结构: SSL协议分为两层,下层为SSL记录协议,上层为SSL握手协议、SSL密码变化协议和SSL警告协议。 1.下层为SSL记录协议,主要作用是为高层协议提供基本的安全服务 建立在可靠的传输之上,负责对上层的数据进行分块…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...
