LC-980. 不同路径 III(回溯)
980. 不同路径 III
难度困难291
在二维网格 grid 上,有 4 种类型的方格:
-
1表示起始方格。且只有一个起始方格。 -
2表示结束方格,且只有一个结束方格。 -
0表示我们可以走过的空方格。 -
-1表示我们无法跨越的障碍。
返回在四个方向(上、下、左、右)上行走时,从起始方格到结束方格的不同路径的数目**。**
每一个无障碍方格都要通过一次,但是一条路径中不能重复通过同一个方格。
示例 1:
输入:[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
输出:2
解释:我们有以下两条路径:
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)
示例 2:
输入:[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
输出:4
解释:我们有以下四条路径:
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)
示例 3:
输入:[[0,1],[2,0]]
输出:0
解释:
没有一条路能完全穿过每一个空的方格一次。
请注意,起始和结束方格可以位于网格中的任意位置。
提示:
1 <= grid.length * grid[0].length <= 20
DFS回溯
https://leetcode.cn/problems/unique-paths-iii/solution/liang-chong-fang-fa-hui-su-zhuang-tai-ya-26py/
class Solution {int m, n;int[][] grid;public int uniquePathsIII(int[][] grid) {this.grid = grid;m = grid.length;n = grid[0].length;int cnt0 = 0, sx = -1, sy = -1;for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if(grid[i][j] == 0) cnt0++;else if(grid[i][j] == 1){sx = i; sy = j; // 起点}}}return dfs(sx, sy, cnt0 + 1); // 算上起点}// 定义 dfs(z,y,let) 表示从 (a,y) 出发,还剩下 let 个无障碍方格 (不含终点)需要访问时的不同路径个数public int dfs(int x, int y, int left){if(x < 0 || x >= m || y < 0 || y >= n || grid[x][y] < 0)return 0; // 不合法if(grid[x][y] == 2){ // 到达终点return left == 0 ? 1 : 0;} grid[x][y] = -1; // 标记成访问过,因为题目要求「不能重复通过同一个方格」int ans = dfs(x-1, y, left-1) + dfs(x, y-1, left-1) +dfs(x+1, y, left-1) + dfs(x, y+1, left-1);grid[x][y] = 0; // 恢复现场return ans;}
}
相关文章:
)
LC-980. 不同路径 III(回溯)
980. 不同路径 III 难度困难291 在二维网格 grid 上,有 4 种类型的方格: 1 表示起始方格。且只有一个起始方格。 2 表示结束方格,且只有一个结束方格。 0 表示我们可以走过的空方格。 -1 表示我们无法跨越的障碍。 返回在四个方向&…...
软件测试缺陷报告
缺陷报告是描述软件缺陷现象和重现步骤地集合。软件缺陷报告Software Bug Report(SBR)或软件问题报告Software Problem Report(SPR) 作用:缺陷报告是软件测试人员的工作成果之一,体现软件测试的价值缺陷报…...

vue js-table2excel 导出excel 可带多张图片
1.安装js-table2excel插件: npm install js-table2excel2.使用 2.1:引入 import table2excel from js-table2excel;2.2:导出函数 function exportExcel() {console.log(导出, table2excel);const column [{title: 二维码id,key: fname,type: text,},{title: 二维…...

HTML 基础标签
前言 当今互联网时代,网页是我们获取信息、交流和展示自己的重要渠道之一。而HTML(超文本标记语言)作为构建网页的基础,学习掌握HTML标签成为了必不可少的技能。 标题标签 <h1>~<h6>:这是用来定义标题的…...

Nginx使用proxy_cache指令设置反向代理缓存静态资源
场景 CentOS7中解压tar包的方式安装Nginx: CentOS7中解压tar包的方式安装Nginx_centos7 tar文件 怎么load_霸道流氓气质的博客-CSDN博客 参考上面流程实现搭建Nginx的基础上,实现静态资源的缓存设置。 注意上面安装时的目录是在/opt/nginx目录下&…...
React安装ant design组件库,并使用
ant design是一个很棒的组件库,官方地址:快速上手 - Ant Design 但是如何在React里面用起来,好像并不是很顺畅,没有像Vue里面那么友好,因为我踩过这个坑,虽然安装很简单,但是想要出样式&#x…...
Leetcode | 有效的括号、最长有效括号
一、有效的括号 给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。每个右括号都有一个对应…...
思科模拟器配置静态路由(下一跳使用IP)
Router0配置代码:##端口配置 Router(config)#int fastEthernet 0/0 Router(config-if)#ip address 192.168.10.254 255.255.255.0 Router(config-if)#no shutdown Router(config-if)#int fastEthernet 0/1 Router(config-if)#ip address 192.168.20.1 255.255.255.2…...

MyBatis -- 执行流程
传统JDBC开发 代码样例 import java.sql.*;public class JdbcExample {public static void main(String[] args) {Connection conn DriverManager.getConnection("jdbc:mysql://localhost:3306/mydatabase", "username", "password");// 创建…...

springboot背诵
1、springboot简介 2、spring注解 Bean: Configuration: Component: Controller: Service: Repository: ComponentScan: Import: Conditional: ConfigurationProperties&…...
WebGL: 几个入门例子
本文罗列几个WebGL入门例子,用于帮助WebGL学习。 例子1:绘制三角形 <!DOCTYPE HTML> <html loang"en"><head><title>Triangle</title><meta charset"utf-8"><script>var gl;var canvas…...

App Cleaner Uninstaller for Mac 苹果电脑软件卸载工具
App Cleaner & Uninstaller 是一款非常有用的 Mac 应用程序清理和卸载工具。它可以彻底地清理系统中的应用程序、扩展和残留文件,以释放磁盘空间并优化系统性能。 此外,它还提供了磁盘空间监控和智能清理建议等功能,使用户可以轻松地管理…...
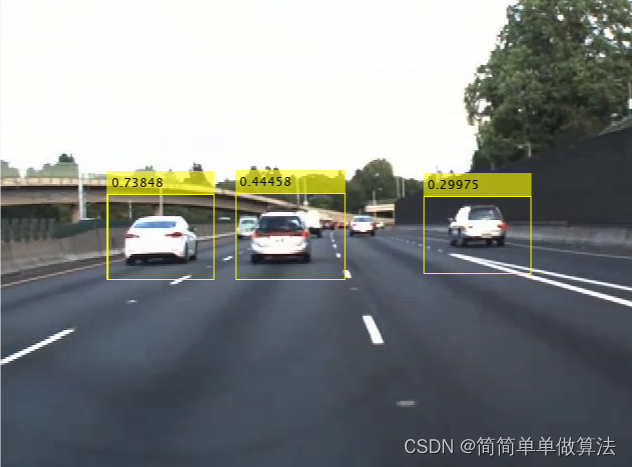
基于Yolov2深度学习网络的车辆检测算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1. 卷积神经网络(CNN) 4.2. YOLOv2 网络 4.3. 实现过程 4.4. 应用领域 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 MATLAB2022A 3.部分核心…...

Java的I/O类库- NIO
Java NIO(New I/O)是Java平台提供的一种用于非阻塞I/O操作的API。它引入了一组新的Java类,用于实现高性能的、非阻塞的I/O操作,以替代传统的阻塞式I/O(IO Blocking)模型。Java NIO的核心是基于Channel&…...
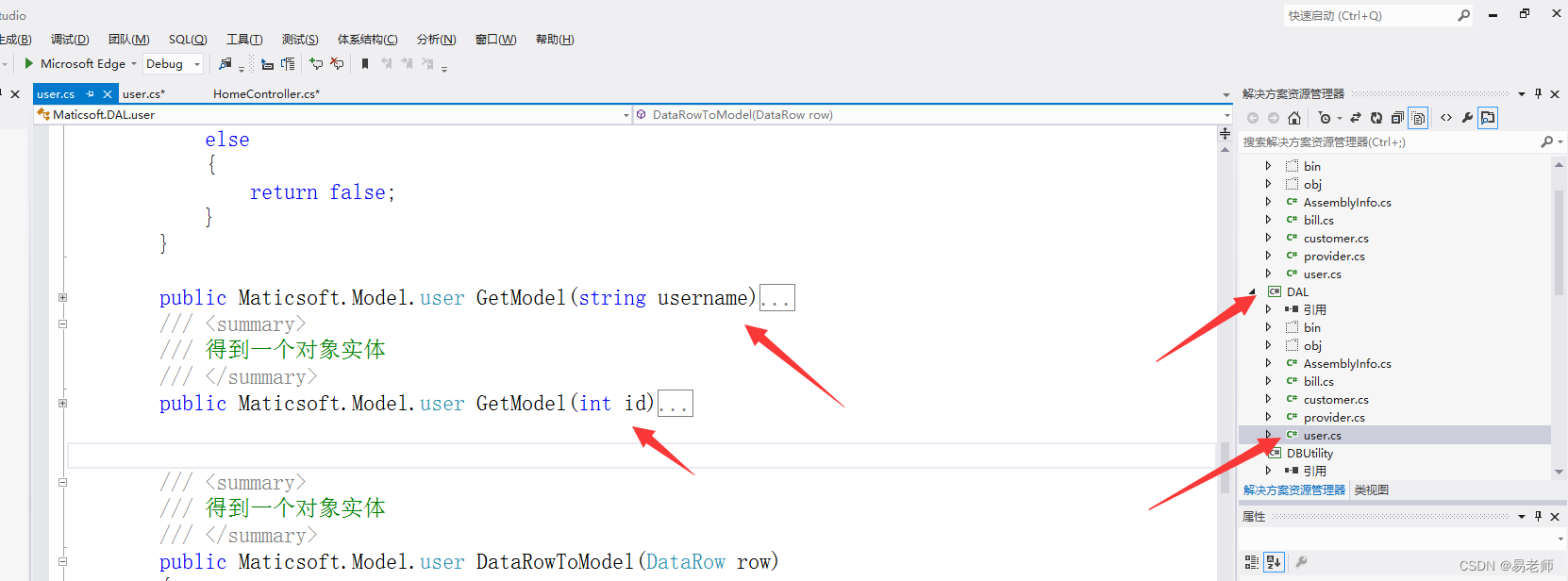
【ASP.NET MVC】使用动软(三)(11)
一、问题 上文中提到,动软提供了数据库的基本操作功能,但是往往需要添加新的功能来解决实际问题,比如GetModel,通过id去查对象: 这个功能就需要进行改进:往往程序中获取的是实体的其他属性,比如…...

基于MATLAB长时间序列遥感数据植被物候提取与分析
MATLAB MATLAB是美国MathWorks公司出品的商业数学软件,用于数据分析、无线通信、深度学习、图像处理与计算机视觉、信号处理、量化金融与风险管理、机器人,控制系统等领域。 [1] MATLAB是matrix&laboratory两个词的组合,意为矩阵工厂&a…...

K8S deployment 重启的三种方法
一般重启deployment,常规操作是删掉对应的pod, 但如果有多个副本集的话,一个个删很麻烦。 除了删除pod,还可以: 方案一: 加上环境变量 kubectl patch deploy <deployment-name> -p {"spec":{"…...

解决Linux下PyCharm无法新建文件
一、问题描述 如图,在Ubuntu Linux系统中使用pycharm管理项目时,提示无法新建.py源文件: 二、问题解决 将问题定性为文件夹(目录)权限问题,在终端中打开项目文件夹的上级目录,将整个项目目录的…...

规则引擎技术解决方案
1 概述 1.1 规则引擎的背景 业务系统在应用过程中,常常包含着要处理“复杂、多变”的部分,这部分往往是“业务规则”或者是“数据的处理逻辑”。因此这部分的动态规则的问题,往往需要可配置,并对系统性能和热部署有一定的要求。从…...

2023奇安信天眼设备--面试题
1.在天眼分析平台网络协议中sip、dip、sport、dport字段表示的含义是什么? sip 源IP、dip 目的IP、sport 源端口、dport 目的端口 2.在天眼分析平台DNS协议中dns type字段表示的含义是? dns type表示DNS请求类型 0代表DNS请求,1代表DNS响应 3.dns_typ…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...
