python中的matplotlib画饼图(数据分析与可视化)
直接开始
1、先安装pandas和matplotlib
pip install pandas
pip install matplotlib
2、然后在py文件中导入
import pandas as pd
import matplotlib.pyplot as plt3、然后直接写代码
import pandas as pd
import matplotlib.pyplot as pltpd.set_option("max_columns",None)
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False# 各类别的标签
labels = ['中专', '大专', '本科', '硕士','其他']
data = [25.15,37.24,33.36,3.68,0.57]
# 饼状图中各部分的颜色
colors = ['yellowgreen', 'gold', 'lightskyblue', 'lightcoral','blue']
#对比各个部分的凸显程度
explode = (0.1,0.1,0.1,0.1,0.1)
# 绘制饼状图
plt.pie(data, labels=labels, colors=colors, textprops = {'fontsize':12, 'color':'k'},explode=explode, shadow=True,startangle=30, autopct="%0.2f%%",pctdistance=0.5)plt.show()结束,不用谢!
相关文章:
)
python中的matplotlib画饼图(数据分析与可视化)
直接开始 1、先安装pandas和matplotlib pip install pandas pip install matplotlib2、然后在py文件中导入 import pandas as pd import matplotlib.pyplot as plt3、然后直接写代码 import pandas as pd import matplotlib.pyplot as pltpd.set_option("max_columns&…...

用Rust实现23种设计模式之 职责链模式
关注我,学习Rust不迷路!! 优点 解耦:职责链模式将请求发送者和接收者解耦,使得多个对象都有机会处理请求,而不是将请求的发送者和接收者紧密耦合在一起。灵活性:可以动态地改变或扩展处理请求…...

进销存管理中的技术创新和数字化转型
在进销存管理中,技术创新和数字化转型可以通过以下具体的应用案例来实现: 自动化仓储系统:利用自动化技术和机器人系统来管理仓库操作,包括货物的装卸、分拣和存储。这可以提高仓库的运作效率,减少人力成本࿰…...

与“云”共舞,联想凌拓的新科技与新突破
伴随着数字经济的高速发展,IT信息技术在数字中国建设中起到的驱动和支撑作用也愈发凸显。特别是2023年人工智能和ChatGPT在全球的持续火爆,更是为整个IT产业注入了澎湃动力。那么面对日新月异的IT信息技术,再结合疫情之后截然不同的经济环境和…...
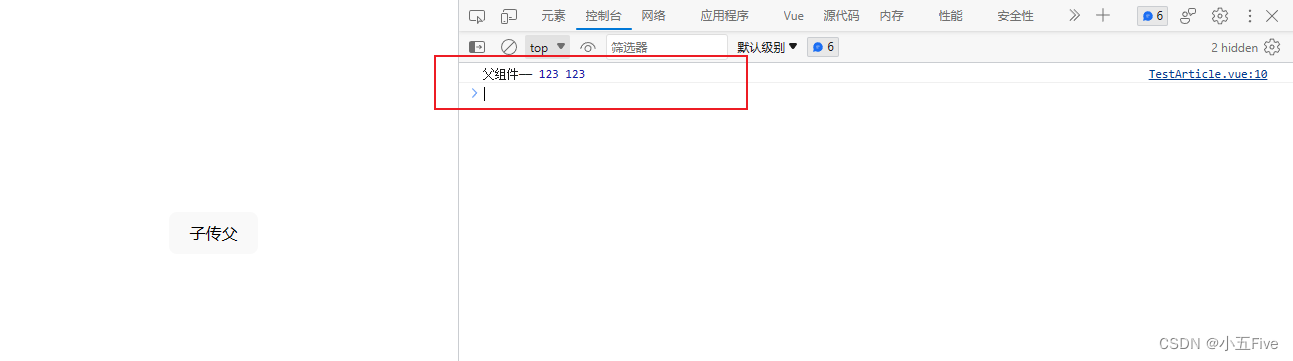
【超细节】Vue3组件事件怎么声明,defineEmits与emit
目录 前言 一、基本语法 1. 子组件触发 2. 父组件监听 二、 事件参数 1. 传值 2. 接收值 三、 事件校验 四、注意事项 前言 组件事件是 Vue 组件之间进行通信的一种方式。它允许一个组件触发一个自定义事件,并且其他组件可以监听并响应这个事件。 一、基本…...

java Selenium 实现简单的网页操作
官方文档:入门指南 | Selenium Selenium是一个用于Web应用测试的工具。Selenium测试直接运行在浏览器中,就像真正的用户在操作一样。 所以使用这个前端测试话工具,可以自动化做很多事情,比如自动化抓取网页内容,俗称网…...

(数据库系统概论|王珊)第一章绪论-第一节:数据库系统概论
目录 一:四大基本概念 (1)数据(Data) (2)数据库(DataBase,DB) (3)数据库管理系统(DataBase Management System,DBMS) (4)数据库系统(Database System,DBS…...
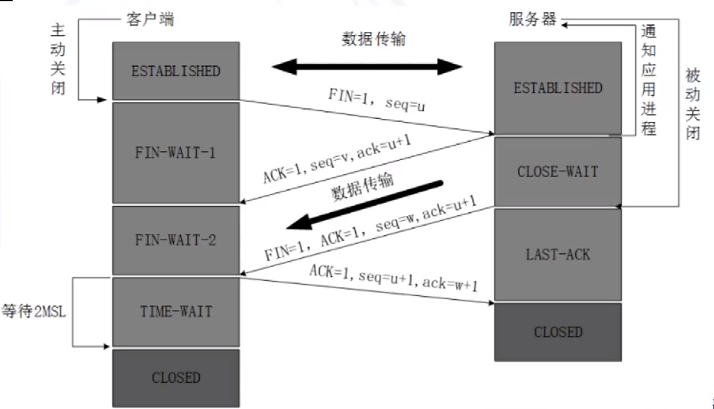
深入理解TCP三次握手:连接可靠性与安全风险
目录 导言TCP简介和工作原理的回顾TCP三次握手的目的和步骤TCP三次握手过程中可能出现的问题和安全风险为什么TCP三次握手是必要的?是否可以增加或减少三次握手的次数?TCP四次挥手与三次握手的异同点 导言 在网络通信中,TCP(Tra…...

基于人工智能的智能矿山解决方案
什么是智能矿山? 智能矿山是一种运用先进技术和智能化系统来管理和监控矿山运营的概念。它利用传感器、无线通信、数据分析和人工智能等技术,实现对矿山内部各个环节的实时监测、自动化控制和智能决策,从而提高矿山的效率、安全性和可持续性。…...
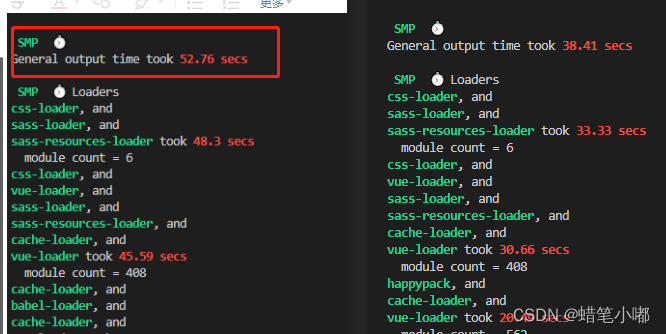
vue-cli3项目优化
首先添加两个量化的插件,方便对项目目前的情况进行分析: 1.添加speed-measure-webpack-plugin插件 —量化的指标可以看出前后对比 使用步骤: 安装speed-measure-webpack-plugin依赖 npm install speed-measure-webpack-plugin -D配置vue.c…...
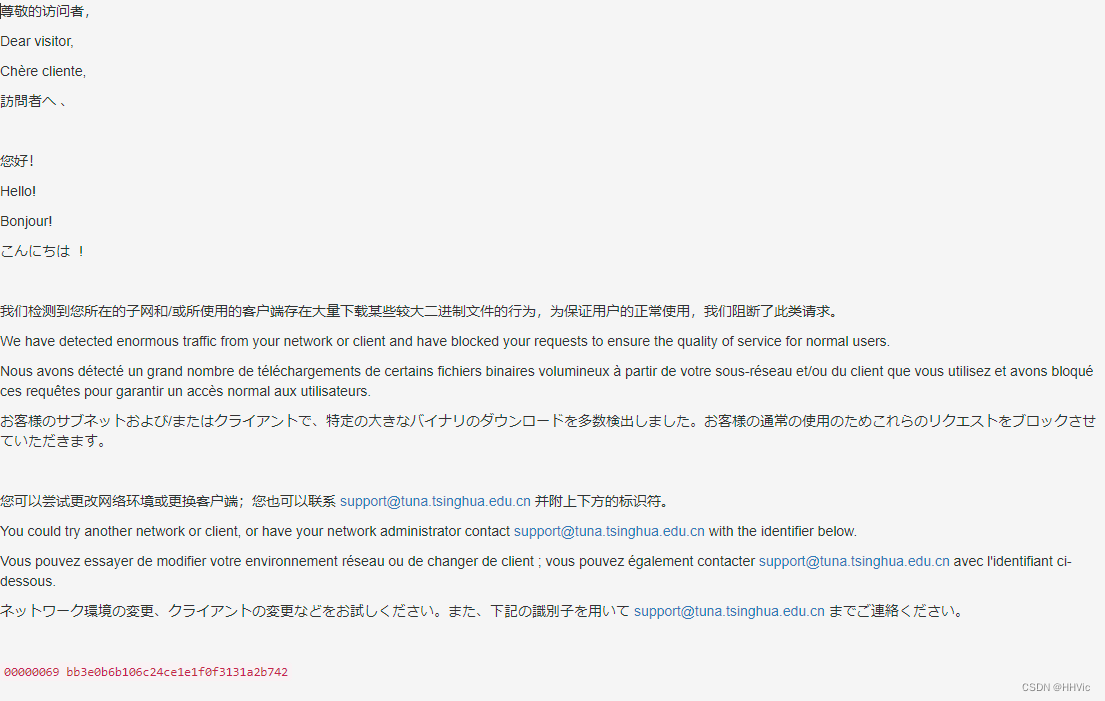
Windows环境下VSCode安装PlatformIO Cero报错ERROR: HTTP error 403 while getting
安装PlatformIO插件成功,初始化失败 错误信息判断问题尝试访问https://pypi.tuna.tsinghua.edu.cn/simple/platformio/成功点击文件后报错如下: 解决问题- 换源 ( Windows下有两个地方需要更改)cmd命令行Pip文件 总结:…...
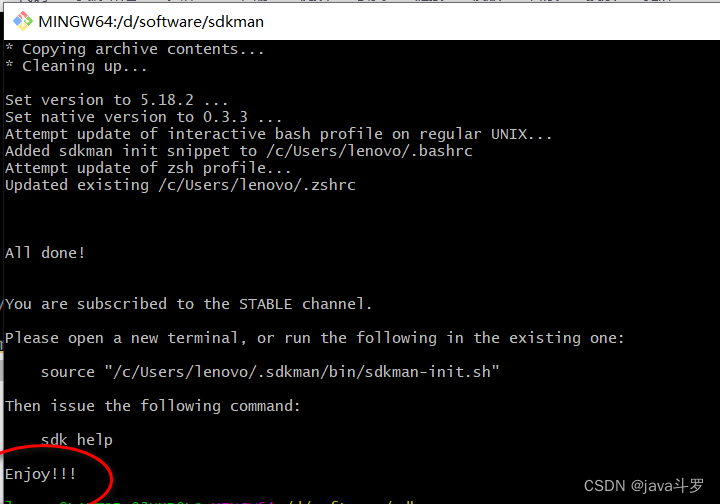
git bash 安装sdkadmin
1.下载相关安装包,复制到git 安装目录 D:\software\Git\mingw64\bin 2. 运行 curl -s "https://get.sdkman.io" | bash...

如何在IEEE论文中添加伪代码pseudocode
前言 记录写论文过程中需要重复用的一些小技巧: 一、如何在IEEE论文中添加伪代码pseudocode pseudocode是经常需要在论文中使用的流程图,掌握如何写伪代码图是必须得。 1.引入库 代码如下(示例): # 头部添加不可少的…...

【css】css隐藏元素
display:none:可以隐藏元素。该元素将被隐藏,并且页面将显示为好像该元素不在其中。visibility:hidden: 可以隐藏元素。但是,该元素仍将占用与之前相同的空间。元素将被隐藏,但仍会影响布局。 代码: <!…...

JUC并发编程(二)ForkJoinPool、Future、CompletableFuture、CAS
文章目录 ForkJoin分治工作窃取ForkJoinPool与ThreadPoolExecutor使用案例不带返回值的计算--RecursiveAction带返回值的计算--RecursiveTask Future 异步回调烧水案例join实现FutureTask实现 CompletableFuture为什么叫CompletableFuture?创建异步任务supplyAsyncrunAsync获取…...

大数据课程F2——HIve的安装操作
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解HIve的安装概念; ⚪ 掌握HIve安装步骤和Linux常用命令; ⚪ 掌握HIve安装的连接池jar包冲突和日志打印jar包冲突; ⚪ 掌握HIve安装的Hadoop安装配置; ⚪ 掌握HIve安装的JDK安装配…...
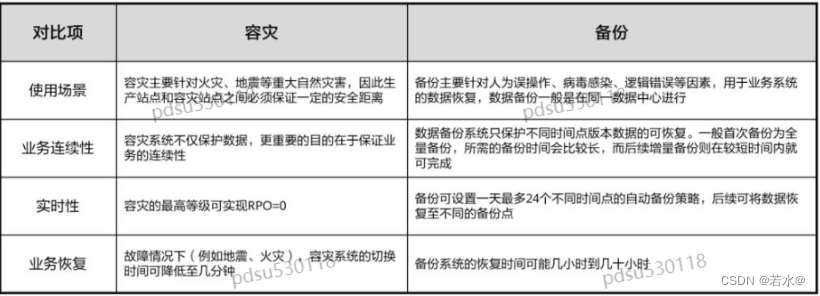
华为云hcip核心知识笔记(存储服务规划)
云上存储 : 云硬盘:基于分布式架构,可弹性扩展的虚拟块存储服务 注意事项 挂载云硬盘实例和云硬盘必须在同一区域,否则挂载失败文件存储服务:完全托管的共享文件存储 可以为多个实例实现共享访问,不同vpc中可以进行对…...

四、JVM-对象内存模型
Java对象内存模型 一个Java对象在内存中包括3个部分:对象头、实例数据和对齐填充 数据 内存 – CPU 寄存器 -127 补码 10000001 - 11111111 32位的处理器 一次能够去处理32个二进制位 4字节的数据 64位操作系统 8字节 2的64次方的寻址空间 指针压缩技术 JDK1.6出…...

2023-08-05 LeetCode每日一题(合并两个有序链表)
2023-08-05每日一题 一、题目编号 21. 合并两个有序链表二、题目链接 点击跳转到题目位置 三、题目描述 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 示例1: 示例2: 示例3: …...
【每天40分钟,我们一起用50天刷完 (剑指Offer)】第四十七天 47/50
专注 效率 记忆 预习 笔记 复习 做题 欢迎观看我的博客,如有问题交流,欢迎评论区留言,一定尽快回复!(大家可以去看我的专栏,是所有文章的目录) 文章字体风格: 红色文字表示&#…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...
