二维数组对角线判断
二维数组对角线判断
对于两个点(x1, y1)和(x2, y2)。如何判断二者是否在同一条正对角线,反对角线,或者正或反对角线上?
正对角线判断
x2-x1 = y2 -y1
证明:任意一点(x1+k, y1+k),(k为整数)与(x1, y1)在同一条正对角线上。
x2=x1+k, y2=y1+k
故 k= x2-x1 = y2-y1
反对角线判断
x2-x1 = y1 -y2 = - (y2 -y1)
证明:任意一点(x1-k, y1+k),(k为整数)与(x1, y1)在同一条正对角线上。
x2=x1-k, y2=y1+k
故 - k= x2-x1 = y1-y2
正或反对角线判断
abs(x2-x1)=abs( y2 -y1);
x2-x1 = y2 -y1 || x2-x1 = -( y2 -y1) 即 x2-x1=±(y2-y1)即 abs(x2-x1)=abs( y2 -y1);
相关文章:

二维数组对角线判断
二维数组对角线判断 对于两个点(x1, y1)和(x2, y2)。如何判断二者是否在同一条正对角线,反对角线,或者正或反对角线上? 正对角线判断 x2-x1 y2 -y1 证明:任意一点(x1k, y1k),(k…...
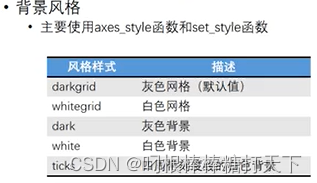
数据可视化(六)多个子图及seaborn使用
1.多个子图绘制 #绘制多个子图 #subplot(*args,**kwargs) 每个subplot函数只能绘制一个子图 #subplots(nrows,ncols) #fig_add_subplot(行,列,区域) #绘制子图第一种方式 plt.subp…...
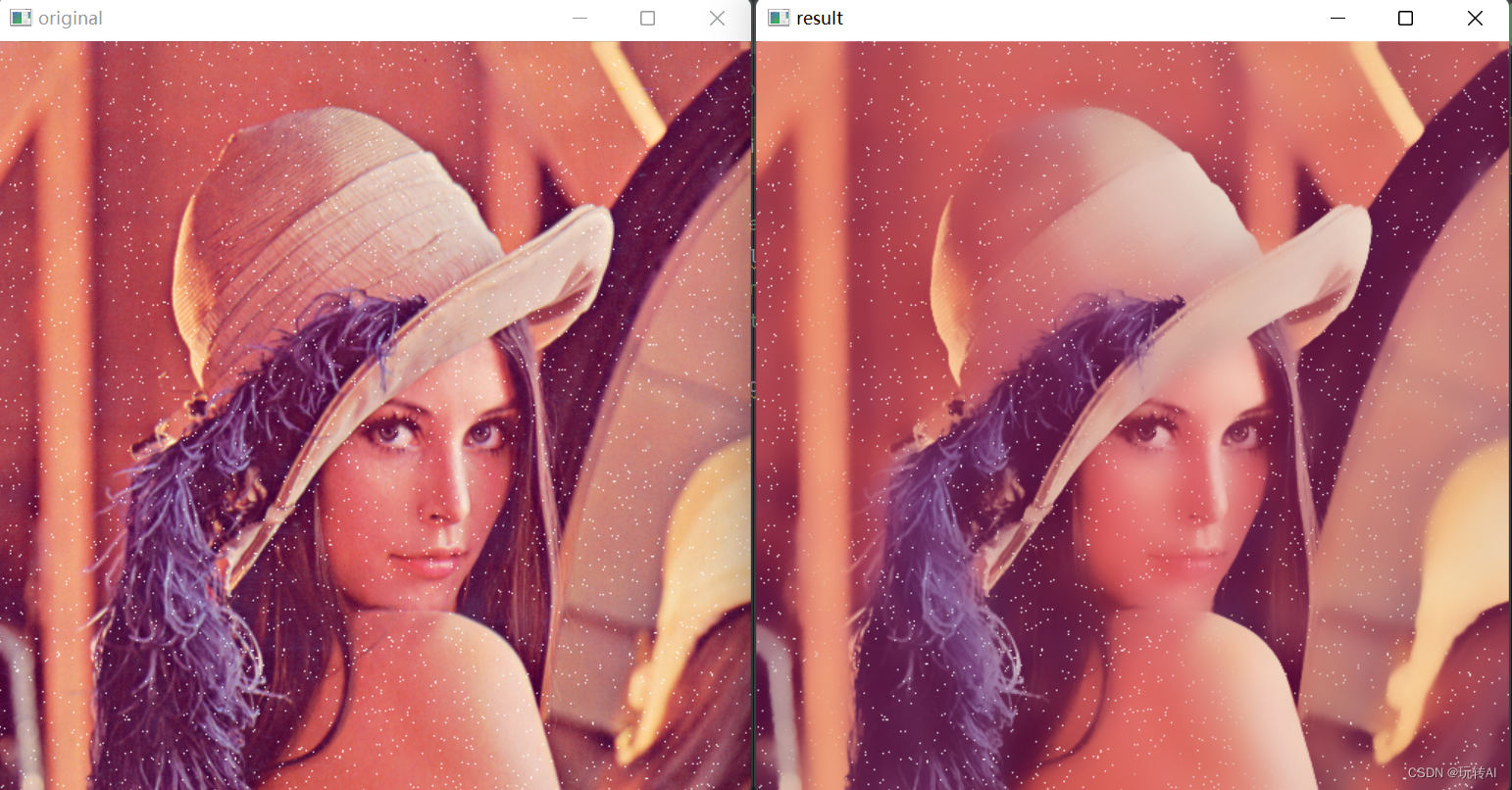
opencv-34 图像平滑处理-双边滤波cv2.bilateralFilter()
双边滤波(BilateralFiltering)是一种图像处理滤波技术,用于平滑图像并同时保留边缘信息。与其他传统的线性滤波方法不同,双边滤波在考虑像素之间的空间距离之外,还考虑了像素之间的灰度值相似性。这使得双边滤波能够有…...

Leetcode 268. Missing Number
Problem Given an array nums containing n distinct numbers in the range [0, n], return the only number in the range that is missing from the array. Algorithm Sum all the numbers as x x x and use n ( n 1 ) 2 − x \frac{n(n1)}{2} - x 2n(n1)−x. Code …...
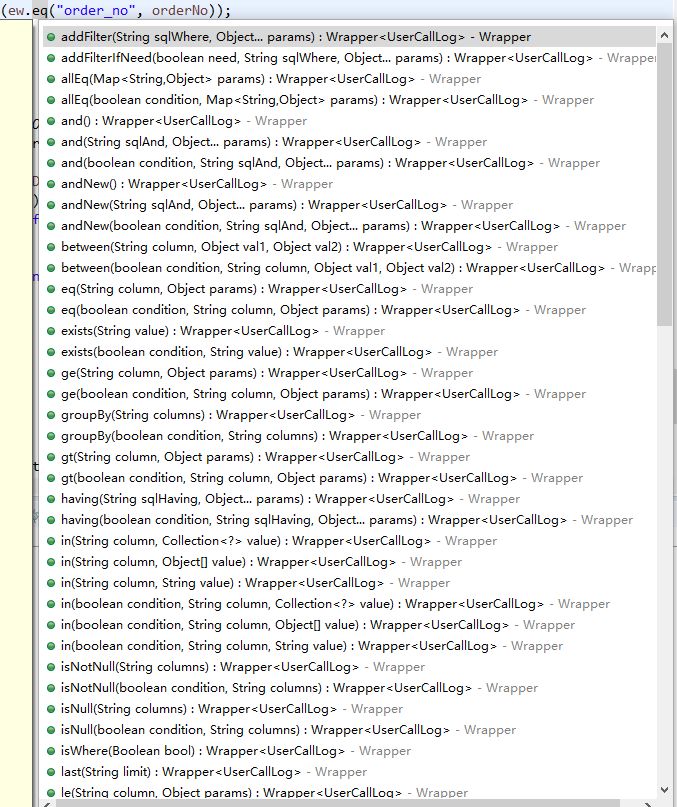
MybatisPlus实战笔记
概述 Mybatis支持定制化SQL、存储过程以及高级映射,避免几乎所有的 JDBC 代码和手动设置参数以及获取结果集。可以使用简单的 XML 或注解来配置和映射原生信息,将接口和Java的POJO映射成数据库中的记录。 缺点: SQL工作量很大,尤…...

Android Studio 报错:Failed to create Jar file xxxxx.jar
通过分析,新下载的项目没有project/gradle目录,故通过其他项目复制到当前项目,就解决了该问题。 同时也出现了新的问题 Unable to start the daemon process.The project uses Gradle 4.1 which is incompatible with Java 11 or newer.原因…...
Django实现音乐网站 ⑸
使用Python Django框架制作一个音乐网站, 本篇主要是配置媒体资源设置。 目录 配置介绍 设置媒体资源 创建媒体资源目录 修改settings.py 注册媒体资源路由 总结 配置介绍 静态资源是指项目配置的js/css/image等系统常用文件。对于一些经常变动的资源&#x…...

基于VUE3+Layui从头搭建通用后台管理系统(前端篇)七:工作台界面实现
一、本章内容 本章实现工作台界面相关内容,包括echart框架引入,mock框架引入等,实现工作台界面框架搭建,数据加载。 1. 详细课程地址: 待发布 2. 源码下载地址: 待发布 二、界面预览 三、开发视频 基于VUE3+Layui从头搭建通用后台管理系统合集-工作台界面布局实现 五、…...
前端vue uni-app自定义精美海报生成组件
在当前技术飞速发展的时代,软件开发的复杂度也在不断提高。传统的开发方式往往将一个系统做成整块应用,一个小的改动或者一个小功能的增加都可能引起整体逻辑的修改,从而造成牵一发而动全身的情况。为了解决这个问题,组件化开发逐…...

高通滤波器,低通滤波器
1.高通滤波器是根据像素与邻近像素的亮度差值来提升该像素的亮度。 import cv2 import numpy as np from scipy import ndimagekernel_3_3 np.array([[-1,-1,-1],[-1,8,-1],[-1,-1,-1]]) print(kernel_3_3) kernel_5_5 np.array([[-1,-1,-1,-1,-1],[-1,1,2,1,-1],[-1,2,4,2,-…...
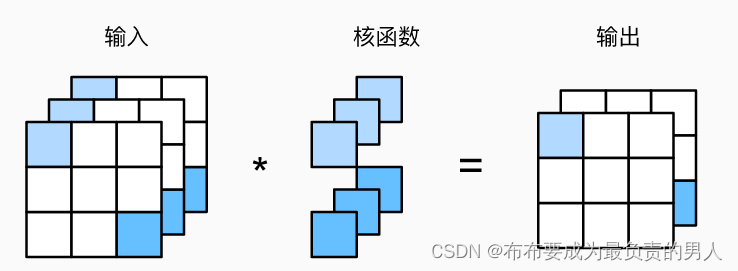
机器学习深度学习——卷积的多输入多输出通道
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——从全连接层到卷积 📚订阅专栏:机器学习&&深度学习 希望文章对你们有所帮…...

HTML5中Canvas学习笔记:Canvas
目录 一、HTML中Canvas画图strokeStyle 和 fillStyle 的区别是什么? 二、如何设置一幅canvas图中某个颜色透明? 三、H5 canvas中strokeRect参数如果是小数,如何处理? 四、H5 Canvas中如何画圆角矩形框? 一、HTML中…...

Windows安装子系统Linux
Windows安装子系统(Linux ubuntu) 安装条件步骤1.安装WSL命令2.设置Linux用户名和密码3.写个简单的.c程序看看4.如何互传文件 安装条件 Windows 10版本2004及更高的版本才能安装。 步骤 1.安装WSL命令 我们可以使用WSL来安装子系统 Linux ubuntu(默认是这个)。 …...

C 语言的 pow() 函数
作用: Calculates x raised to the power of y. 函数原型: double pow( double x, double y ); Required Header: <math.h> Compatibility: ANSI Return Value pow returns the value of x y x^{y} xy. No error message is printed on overflow or underflow. Paramete…...

socket 基础
Socket是什么呢? ① Socket通常也称作“套接字”,用于描述IP地址和端口,是一个通信链的句柄。应用程序通常通过“套接字”向网络发出请求或者应答网络请求。 ② Socket是连接运行在网络上的两个程序间的双向通信的端点。 ③ 网络通讯其实指…...
、一些概念的理解---90%响应时间、事务、并发)
JMeter(二十五)、一些概念的理解---90%响应时间、事务、并发
Jmeter中一些概念的理解——90%响应时间、事务、并发 一、90%响应时间(参考虫师博客) 90%Line 一组数由小到大进行排列,找到他的第90%个数(假如是12),那么这个数组中有90%的数将小于等于12 。 用在性能测试的响应时间,也就是90%请求响应时间不会超过12 秒。 例如:…...

直播课 | 大橡科技研发总监丁端尘博士“类器官芯片技术在新药研发中的应用”
从类器官到类器官芯片,正在生物科学领域大放异彩。 药物研发需要新方法 众所周知,一款新药是一个风险大、周期长、成本高的艰难历程,国际上有一个传统的“双十”说法——10年时间,10亿美金,才可能成功研发出一款新药…...
Python中的PDF文本提取:使用fitz和wxPython库(带进度条)
引言: 处理大量PDF文档的文本提取任务可能是一项繁琐的工作。本文将介绍一个使用Python编写的工具,可通过简单的操作一键提取大量PDF文档中的文本内容,极大地提高工作效率。 import wx import pathlib import fitzclass PDFExtractor(wx.Fr…...

mysql 将字段值+1或自增
一、解决方式: SET var 1; UPDATE jes_menu_info SET MENU_SORT (var : var 1) WHERE ss_idACC; 二、解读用户变量,在客户端链接到数据库实例整个过程中用户变量都是有效的。 MySQL中用户变量不用事前申明,在用的时候直接用“变量名”使…...

组合总和——力扣39
文章目录 题目描述回溯 题目描述 回溯 class Solution { public:vector<vector<int>> res;vector<int> seq; void dfs(vector<int>& nums, int pos, int target){if(target0){res.emplace_back(seq);return;}if(posnums.size()){return;}//直接跳过…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
