Thunar配置自定义动作
Add “Copy To” and “Move To” custom actions in Thunar file manager | For the record
1.在此打开终端
图标-应用程序:utilities-terminal
命令:exo-open --working-directory %f --launch TerminalEmulator
文件类型:*
目录
2.右键增加移动到:
图标-原始:stock_folder-move
命令:mv %F "$(zenity --file-selection --directory)"
文件类型:*
非目录
相关文章:

Thunar配置自定义动作
Add “Copy To” and “Move To” custom actions in Thunar file manager | For the record 1.在此打开终端 图标-应用程序:utilities-terminal 命令:exo-open --working-directory %f --launch TerminalEmulator 文件类型:* 目录 2.右键增…...
Python 开发工具 Pycharm —— 使用技巧Lv.3
单步执行调试 1: 鼠标左键单击红点是断点行 2:甲虫样式是进行调试方式运行,鼠标左键单击点击 3: 单步运行图标,点击让程序运行一行 4: 步入步出,可以进入当前代码行函数内 5:重新运行…...
51单片机(普中HC6800-EM3 V3.0)实验例程软件分析 实验三 LED流水灯
目录 前言 一、原理图及知识点介绍 二、代码分析 知识点五:#include 中的库函数解析 _crol_,_irol_,_lrol_ _cror_,_iror_,_lror_ _nop_ _testbit_ 前言 第一个实验:51单片机(普中HC6800-EM3 V3.0…...

深度学习与计算机相结合:直播实时美颜SDK的创新之路
时下,实时美颜技术就成为了直播主们的得力工具,它可以在直播过程中即时处理视频画面。而支持实时美颜功能的SDK更是推动了这项技术的发展,让直播主和普通用户都能轻松使用美颜功能。 一、美颜技术的演进 早期的美颜技术主要依赖于简单的图…...

Unity寻找子物体的方法
1.GetComponentsInChildren() 查找单个子物体 GameObject childObjectGetComponentInChildren<Transform>(); 查找多个子物体 Transform[] myTransforms GetComponentsInChildren<Transform>(); foreach (var child in myTransforms){ Debug.Log(child.name…...

车载软件架构 —— 车载软件安全启动关键技术解读
车载软件架构 —— 车载软件安全启动关键技术解读 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 没有人关注你。也无需有人关注你。你必须承认自己的价值,你不能站在他人的角度来反对自己。人生…...

2023-08-05——JVM Method Area(方法区)
方法区 Method Area(方法区) 方法区是指被所有线程共享的,字段和方法字节码,以及一些特殊方法,如构造函数,接口代码在此定义,简单的说就是所有的定义方法信息都保存在此区域,此区域…...
【前端知识】React 基础巩固(四十六)——自定义Hook的应用
React 基础巩固(四十六)——自定义Hook的应用 一、自定义Hook的应用 自定义Hook本质上只是一种函数代码逻辑的抽取,严格意义上而言,它并不算React的特性。 实现组件创建/销毁时打印日志 import React, { memo, useEffect, useState } from "react…...
Swish - Mac 触控板手势窗口管理工具[macOS]
Swish for Mac是一款Mac触控板增强工具,借助直观的两指轻扫,捏合,轻击和按住手势,就可以从触控板上控制窗口和应用程序。 Swish for Mac又不仅仅只是一个窗口管理器,Swish具有28个易于使用的标题栏,停靠栏…...

【雕爷学编程】MicroPython动手做(31)——物联网之Easy IoT 2
1、物联网的诞生 美国计算机巨头微软(Microsoft)创办人、世界首富比尔盖茨,在1995年出版的《未来之路》一书中,提及“物物互联”。1998年麻省理工学院提出,当时被称作EPC系统的物联网构想。2005年11月,国际电信联盟发布《ITU互联网…...
C# 简单模拟 程序内部 消息订阅发布功能
文章目录 前言模拟消息订阅发布使用注意事项 前言 我想做个简单的消息发布订阅功能,但是发现好像没有现成的工具类。要么就是Mqtt这种消息订阅发布。但是我只想程序内部进行消息订阅发布,进行程序的解耦。那没办法了,只能自己上了 模拟消息…...

第六章 支持向量机
文章目录 支持向量机间隔和支持向量对偶问题问题推导SMO 核函数实验 支持向量机 ⽀持向量机(Support Vector Machines,SVM) 优点:泛化错误率低,计算开销不⼤,结果易解释。缺点:对参数调节和核…...

Docker基本操作之删除容器Container和删除镜像IMAGE
一、删除容器Container语法 docker rm [OPTIONS] CONTAINER [CONTAINER...]OPTIONS参数说明: -f :通过 SIGKILL 信号强制删除一个运行中的容器。【注意是正在运行的容器实例】-l :移除容器间的网络连接,而非容器本身。-v :删除与容器关联的卷。即删除容…...
vue 3.0 + element-ui MessageBox弹出框的 让文本框显示文字 placeholder
inputPlaceholder:请填写理由, 方法实现如下: this.$prompt(, 是否确认?, { confirmButtonText: 确定, cancelButtonText: 取消, inputPlaceholder:请填写理由, }).then(({ value }) > { if(value null || value ""){ Message({message: 请填…...
QT生成可执行文件的步骤
QT生成可执行文件的步骤 第一步:debug为release,然后进行编译 第二步:添加QT生成必要的库 首先,建立一个新的文件夹,然后将Release中的可执行文件拷贝到新的文件夹中 然后,在新建文件夹中生成必要的库 …...
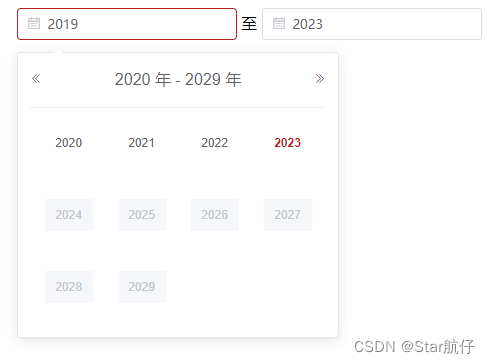
一分钟学会JS获取当前年近五年的年份
先看效果图 上代码: 1、HTML <div><el-date-pickerv-model"queryYearXmgk.startYear"format"yyyy"value-format"yyyy"type"year"placeholder"开始"clearable:picker-options"pickerStartAuditYe…...

14 springboot项目——首页跳转实现
templates里的静态资源无法访问,需要写mvc的配置类或者改application.xml配置文件实现首页访问。这两个方式用其中一种即可,否则会冲突。 14.1 首页跳转方式一 创建配置类,在config包中创建一个mvc的配置类: package jiang.com.s…...
IL汇编语言读取控制台输入和转换为整数
新建一个testcvt.il; .assembly extern mscorlib {}.assembly Test{.ver 1:0:1:0}.module test.exe.method static void main() cil managed{.maxstack 1.entrypointldstr "\n请输入一个数字:"call void [mscorlib]System.Console::Write(string)call st…...
什么是跨链 DeFi?
跨链 DeFi 是指存在于多个不同区块链生态系统之间的金融应用程序生态系统,可以在彼此之间无缝交换数据和通证。 Web3 生态系统已经变得多链化,存在于数百个区块链、二层网络、应用链和其他环境的去中心化应用繁荣发展。虽然多样化的区块链生态系统的推出…...

Linux下C/C++的gdb工具与Python的pdb工具常见用法之对比
1、gdb和pdb分别是什么? 1.1、gdb GDB(GNU Debugger)是一个功能强大的命令行调试工具,由GNU项目开发,用于调试C、C等编程语言的程序。它在多个操作系统中都可以使用,包括Linux、MacOS和Windows࿰…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...
