De Bruijin序列与魔术(二)——魔术《De Bruijin序列》
早点关注我,精彩不错过!
上一篇我们介绍了De Bruijin序列的基本数学内容以及其如何应用在魔术上的一些基本内容,今天我们就来学习一下这个经典的《De Bruijin序列》魔术。
De bruijin序列魔术
先看视频。
视频1 De Bruijin序列的魔术
魔术来源
和这个魔术的缘分,要追溯到大约大学时候,疯狂地学习数学,魔术,以及零星地查到的一点点数学魔术相关的内容。在果壳网上,我看到了一个叫Albert_Jiao的作者,它一系列的数学魔术文章是我那时候难得获得的一点养料。其中一篇就是介绍De Bruijin序列的。后来,在Magical Mathematics一书中,有2~4共3个章节的篇幅都在讨论这个内容,细细去看里面的来龙去脉一定会有很多的收获。这里仅就De Bruijin序列本身以及其魔术应用来描述。
魔术原理分析
这个数学魔术里用的编码,是一套神奇的编码,可以仅由特定位置的一个二进制表达就能推断位置,进而推断出一叠序列固定扑克牌的全部点数和花色,这就是这个魔术的编码通信原理。因为De Bruijin序列的存在,使得这样的编码变得可行。那最后一个问题来了,我们怎么找到一条适合人记忆的Debruijin序列呢?
还是那个原则,人脑是不太善于去记忆没有什么相互联系和逻辑的事物的,因为它会判断,这些东西没有价值,就像我在大学时候死活听不进也背不了有些工科老师上课讲的内容,因为那明明是数理逻辑,泛函分析,欧拉定理,为什么偏偏要给你讲成数字逻辑电路,光学工程,模拟电路?还搞一些莫名其妙,不着本质的概念来包装?可能有人能够接受这样的方式,对不起,我真接受不了。
相反,人们善于记忆有一定规律,甚至美感的事物,它会觉得那是对的,值得记忆的。比如,这个魔术里,我们用n = 5的de bruijin序列为例,能编码长度为32的序列,然后用扑克牌的红色和黑色来代表0,1得到对应的De Bruijin序列,然后,一副只用32张,A~8的扑克牌,可以简单想到的是,恰好可以用其中两位来代表花色,另外两位来代表点数,刚刚好能很合理地用好所有的信息。可问题来了,难道每个位置是哪张牌,真的要靠纯记忆吗?
好在有人已经给出了答案,在上述编码系统里,除了满足De bruijin序列的基本要求(黑色为0,红色为1),是一个可行解,在连续五张牌的首牌上,恰好由前两位代表花色(第一位代表颜色,0为黑色,1为红色(这里和单个二进制的红黑编码对应),第二位是0表示梅花或方块,1表示黑桃或红桃),现在最后一个问题是,后面的牌以怎样的规律推演出来?
我们借鉴线性移位寄存器的做法,每个下一位都由前面的值计算得到:
a(n) = (a(n - 3) + a(n - 5)) % 2,其实就相当于是往前的3,5位取xor的亦或运算,或者是不进位的二进制加法了。
由此得到的De Bruijin序列为(随意选择一个起点即可,比如这里的00000,因为反正这是一个循环序列):
0000100101100111110001101110101
如图所示:
图2 De Bruijin序列魔术编码表
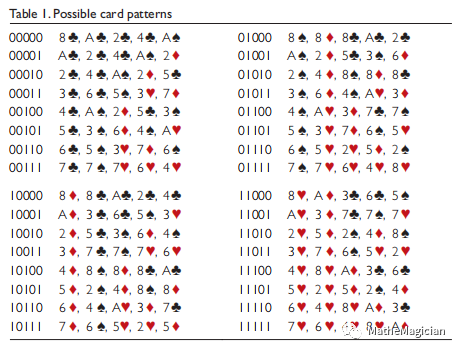
不过遗憾的是,这并不是一个严格的De Bruijin序列,因为它只有31项,00000并没有出现,但是,我们很容易在上面这个序列开头再加上一个0,就得到了32项,也刚好得到了所有需要的编码,只不过在这个0这里,其编码规律被打破了,但此时却构成一个圈,是真的De Bruijin序列了。好在,我们也只需要记住这一个特例就够了。也因为这个原因,原本符合C32群描述的可以随意切牌的循环序列的性质没有了,我们得去记忆这个特殊的位点随着切牌不断移动。至于最后怎么往后推演更容易记忆,我的方案是直接看牌点是否大于等于4(注意这里8相当于0,可以记忆为进位以后溢出了,其底三位的编码就是000)以及颜色是否是黑色,其中一个成立为真,红色,同时真或假为假,黑色。这样记忆几遍以后,能够比较快速和熟练地把所有五张牌推演出来。唯一例外要记住的是,10000以后,得补一个本该是1,但是这里强行插入了一张梅花8,其余照旧。
不过,如果你实在懒得去背这些公式,直接把这个表打印下来去现场秘密地查找也可以,不过得想个理由,比如这里有上帝写给我的密码,或者偷偷地看。我长这么大,唯一看过别人表演这个魔术,就是Albert老师,在我去深大参加的一次数学魔术沙龙里。看来数学魔术日后如我所想,能够在数学家和魔术师中间都被认同和接受,并广泛流传开来,真的不是一件容易的事,至少,我这辈子是打算搭进去了。
不知道大家看了这个牌序花色点数的递推公式有没有些感觉,虽然这里写成了二进制的递推关系,但本质上也是一个牌序的递推关系,不妨我们从牌序本身的角度来理解下这个递推关系,我们有:
N_(i + 1) = Ni << 1 + ([Ni / 4] + [Si / 2]) % 2
S_(i + 1) = Si << 1 + [Ni / 4]
其中N为点数,是0~7之间的数(8的码点是0),Ni<<1是3位二进制数向左的逻辑移位,等价于2Ni % 8,Si << 1是2位二进制数向左的逻辑移位,等价于2Si % 4,因此这个式子又可以写为:
N_(i + 1) = 2Ni % 8 + ([Ni / 4] + [Si / 2]) % 2
S_(i + 1) = 2Si % 4 + [Ni / 4]
它和Richard Osterling序的结构的递推关系式已经很像了,都是一系列花色和点数交叉关联的递推关系,只不过这里限定在了数字8以内,我们到对应章节再详细介绍之。
不过估计熟悉数学魔术的你也想到了,这个数学原理很棒,但是作为一个成熟的魔术表演还远远不足,只拿着阉割的只有32张牌的一叠,而且还奇怪的只有8以内的数字,这数学雕琢和限制的痕迹也太过明显了。但这一切都苦于这个D(2, 5)序列本身的能量。一个简单的处理自然是利用软限制,补齐剩下的20张牌,只不过控制观众选牌的范围在这32张以内即可。
但这总归不完美,我希望能够找到一个接近51~55以内长度的De Bruijin序列,满足核心的一一对应的性质,并有简单的递推公式递推以及容易计算的编码和解码公式能够计算牌的值,方便记忆和使用。于是我开启了一次泛化之旅,看能不能用计算机再搜寻出一些其他的序列,这部分的成果,我们下篇文章来介绍,敬请期待。

我们是谁:
MatheMagician,中文“数学魔术师”,原指用数学设计魔术的魔术师和数学家。既取其用数学来变魔术的本义,也取像魔术一样玩数学的意思。文章内容涵盖互联网,计算机,统计,算法,NLP等前沿的数学及应用领域;也包括魔术思想,流程鉴赏等魔术内容;以及结合二者的数学魔术分享,还有一些思辨性的谈天说地的随笔。希望你能和我一起,既能感性思考又保持理性思维,享受人生乐趣。欢迎扫码关注和在文末或公众号留言与我交流!


扫描二维码
关注更多精彩
De Bruijin序列与魔术(一)——De Bruijin序列简介
这到底是怎么想到的!!!
一道北大强基题背后的故事(七)——特征根公式的来龙去脉
用排列组合来编码通信(七)——《我的5/4张牌的预言》
好魔术背后的秘密

点击阅读原文,往期精彩不错过!
相关文章:

De Bruijin序列与魔术(二)——魔术《De Bruijin序列》
早点关注我,精彩不错过! 上一篇我们介绍了De Bruijin序列的基本数学内容以及其如何应用在魔术上的一些基本内容,今天我们就来学习一下这个经典的《De Bruijin序列》魔术。 De bruijin序列魔术 先看视频。 视频1 De Bruijin序列的魔术 魔术来源…...
ARCGIS地理配准出现的问题
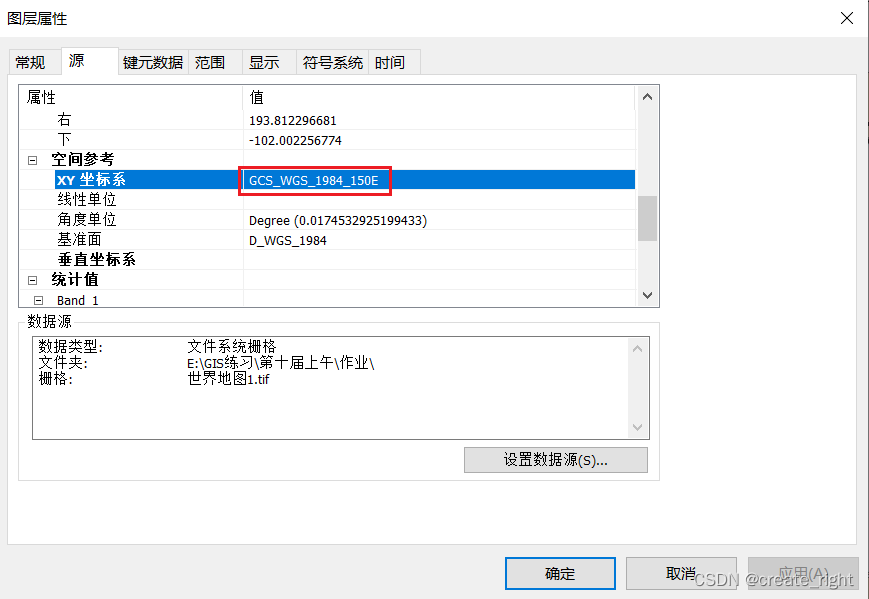
第一种。已有省级行政区矢量数据,在网上随便找一个相同省级行政区图片,利用地理配准工具给图片添加坐标信息。 依次添加省级行政区选择矢量数据、浙江省图片。 此时,图层默认的坐标系与第一个加载进来的省级行政区选择矢量数据的坐标系一致…...
redis原理 6:小道消息 —— PubSub
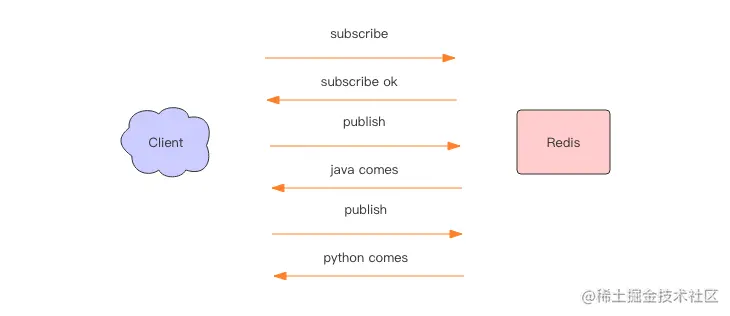
前面我们讲了 Redis 消息队列的使用方法,但是没有提到 Redis 消息队列的不足之处,那就是它不支持消息的多播机制。 img 消息多播 消息多播允许生产者生产一次消息,中间件负责将消息复制到多个消息队列,每个消息队列由相应的消费组…...
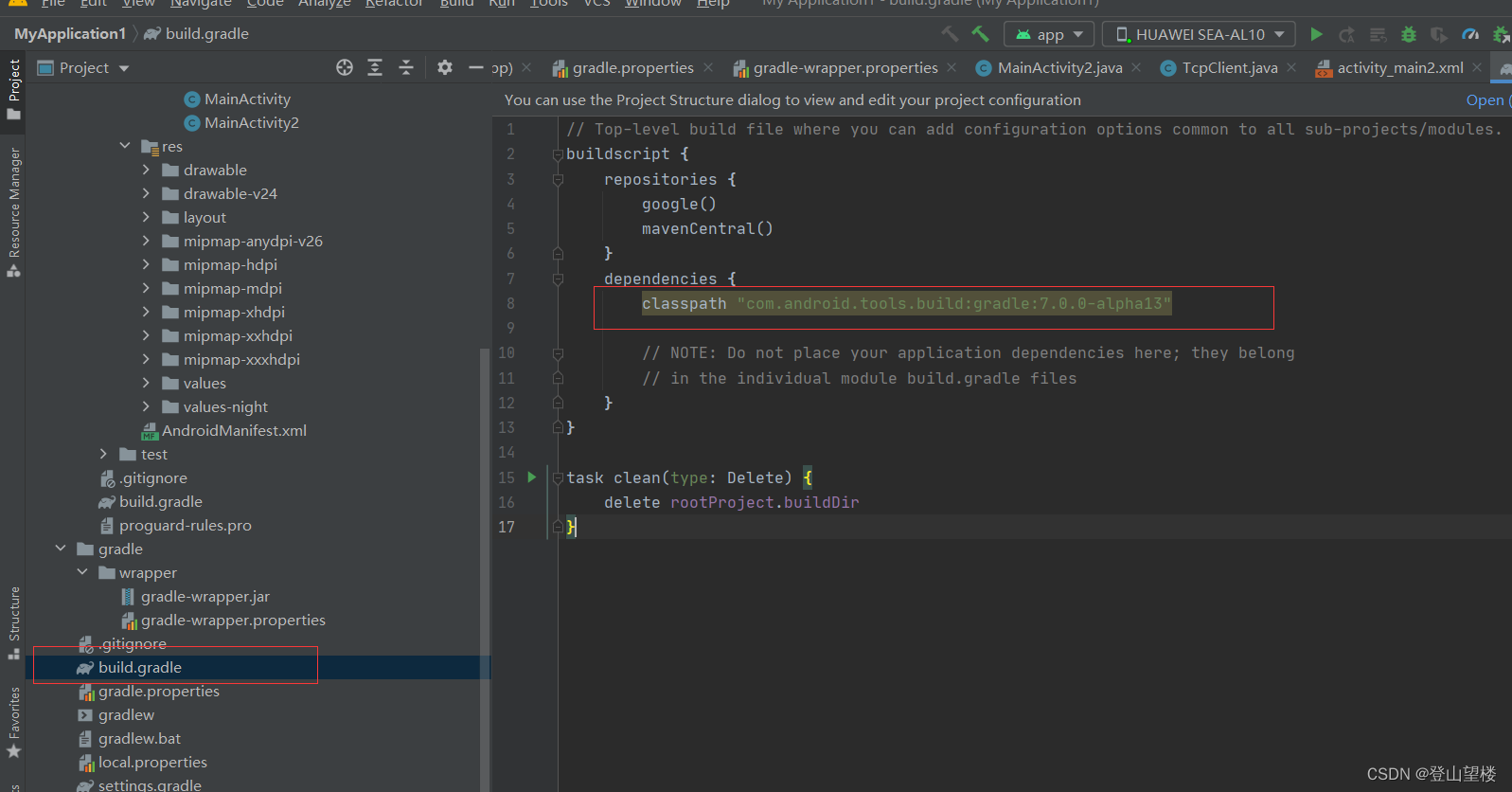
Android Studio 的Gradle版本修改
使用Android Studio构建项目时,需要配置Gradle,与Gradle插件。 Gradle是一个构建工具,用于管理和自动化Android项目的构建过程。它使用Groovy或Kotlin作为脚本语言,并提供了强大的配置能力来定义项目的依赖关系、编译选项、打包方…...

Redis的部分面试题
1.Redis是什么?简述它的优缺点? Redis的字符串类型是通过简单动态字符串SDS来实现的。简单动态字符串是Redis自己实现的一种字符串表示方式,相比于C语言中的传统字符串,它具有以下几个特点: 1. 动态调整大小:简单动态字符串可…...

单通道 6GSPS 16位采样DAC子卡模块--【资料下载】
FMC147是一款单通道6.4GSPS(或者配置成2通道3.2GSPS)采样率的12位AD采集、单通道6GSPS(或配置成2通道3GSPS)采样率16位DA输出子卡模块,该板卡为FMC标准,符合VITA57.4规范,该模块可以作为一个理想…...

Python 文件操作详解
概要 Python进行文件操作,在日常编程中是很常用的。为了方便大家,这里对各种文件操作的知识进行汇总。一文在手,无须它求!来一起学习吧。 一、文件的打开和关闭 open()函数 f1 open(rd:\测试文件.txt, moder, encodingutf-8) c…...

【Rust 基础篇】Rust Never类型:表示不会返回的类型
导言 Rust是一种以安全性和高效性著称的系统级编程语言,其设计哲学是在不损失性能的前提下,保障代码的内存安全和线程安全。在Rust中,Never类型是一种特殊的类型,它表示一个函数永远不会返回。Never类型在Rust中有着重要的应用场…...

error “Component name “*****“ should always be multi-word”解决方案
问题 在 vue-cli 创建的项目中,创建文件并命名后,会报 “Component name "*****" should always be multi-word” 报错; Component name "index" should always be multi-word.eslintvue/multi-word-component-names原…...

前后端开发的区别是什么?
VUE的开发方式为什么和后端的MVC开发方式不一样呢? 实际上,Vue 和后端开发的 MVC(Model-View-Controller)方式是不同的,因为它们面对的问题和场景也不同。 前端与后端的职责不同: 前端和后端的职责和任务不…...
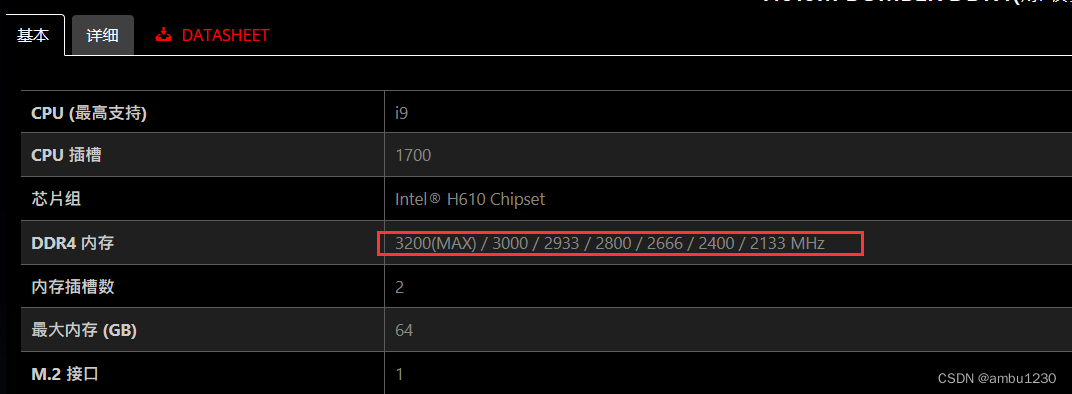
小白电脑装机(自用)
几个月前买了配件想自己装电脑,结果最后无法成功点亮,出现的问题是主板上的DebugLED黄灯常亮,即DRAM灯亮。对于微星主板的Debug灯,其含义这篇博文中有说明。 根据另一篇博文,有两种可能。 我这边曾将内存条和主板一块…...

Quic协议 0-RTT
目录 1、Quic协议 2、Quic直接通过TLS握手进行建立链接,TLS是1.3版本 3.1、通过缓存服务器公钥实现0-RTT,服务器 通过kdf密钥派生机制,来产生会话加密key,保证数据向前安全性 3.2、通过PKN来实现数据重传保证数据完整性&…...

在排序数组中查找元素的第一个和最后一个位置——力扣34
文章目录 题目描述法一 二分查找题目描述 法一 二分查找 int bsearch_1(int l, int r) {while (l < r)<...

python列表处理方法
原始文件: id start end a1 10 19 a1 25 34 a2 89 124 a2 149 167 a2 188 221目的文件: a1 1 10 a1 16 25 a2 1 36 a2 61 79 a2 100 133解释说明: 原始文件是gff3文件的一部分,第一列id是基因的名字,第二列和第三列分…...

【Java】快速入门JVM
文章目录 1. JVM简介2. 类加载简介3. 类加载的过程4. 双亲委派5. GC垃圾回收6. JVM的回收方式7. 分代回收 1. JVM简介 JVM(Java虚拟机)是一个名字为Java的进程,是用于执行Java程序的虚拟机。 JVM会从操作系统中申请一大块内存空间,又把这个内存空间划分…...

C#之Winfrom自定义输入框对话框。
如果你需要一个带有输入框的对话框,并在输入完成后接收输入的值,你可以使用自定义窗体来实现。以下是一个示例代码:创建一个继承自 Form 的自定义窗体类,命名为 InputDialogForm,并将窗体上放置一个文本框(…...

docker制作镜像
docker制作镜像 docker制作镜像有两种: 1.docker build dockerfile 2.基于容器制作镜像 基于容器制作镜像 语法:docker commit options 容器名称 参数: -a:作者 -c:修改dockfile创建的镜像 -m:提交…...

广西茶叶元宇宙 武隆以茶为媒 推动茶文旅产业融合发展
8月4日,重庆市武隆区启动为期3天的“武隆首届玩茶荟”。本次活动以“中国最美玩茶地——武隆”为主题,吸引众多国内知名专家、茶企和茶馆相关负责人,共同探索武隆茶文旅融合发展新路径和新业态。 广西茶叶元宇宙:广西茶叶元宇宙 …...

alibaba.excel库使用
目录 依赖 实体类 Controller Service 所用到的接口及工具类 ExcelUtil ExcelListener DefaultExcelListener DefaultExcelResult ExcelResult JsonUtils SpringUtils StreamUtils ValidatorUtils SpringUtils 使用alibab中的excel库来实现excel的导入、导出 依赖 <de…...

机器学习模型选择评估和超参数调优
如何选择模型?如何评估模型?如何调整模型的超参数?模型评估要在测试集上进行,不能在训练集上进行,否则评估的准确率总是100%。所以,一般我们准备好数据集后,要将其分为训练集和测试集࿰…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
