扩散模型实战(一):基本原理介绍
扩散模型(Diffusion Model)是⼀类⼗分先进的基于物理热⼒学中的扩散思想的深度学习⽣成模型,主要包括前向扩散和反向扩散两个过程。⽣成模型除了扩散模型之外,还有出现较早的VAE(Variational Auto-Encoder,变分⾃编码器)和GAN(Generative Adversarial Net,⽣成对抗⽹络)等。
生成模型
在深度学习中,⽣成模型的⽬标是根据给定的样本(训练数据)⽣成新样本。⾸先给定⼀批训练数据X,假设其服从某种复杂的真实分布p(x),则给定的训练数据可视为从该分布中采样的观测样本x。如果能够从这些观测样本中估计出训练数据的真实分布,不就可以从该分布中源源不断地采样出新的样本了吗?⽣成模型实际上就是这么做的,它的作⽤是估计训练数据的真实分布,并将其假定为q(x)。在深度学习中,这个过程称为拟合⽹络。
那么问题来了,怎么才能知道估计的分布q(x)和真实分布p(x)的差距⼤不⼤呢?⼀种简单的思路是要求所有的训练数据样本采样⾃q(x)的概率最⼤。这种思路实际上来⾃统计学中的最⼤似然估计思想,它也是⽣成模型的基本思想之⼀,因此⽣成模型的学习⽬标就是对训练数据的分布进⾏建模。
扩散过程
最⼤似然估计思想已经在⼀些模型(如VAE)上应⽤并取得了不错的效果。扩散模型可看作⼀个更深层次的VAE。扩散模型的表达能⼒更加丰富,⽽且其核⼼在于扩散过程。
扩散的思想来⾃物理学中的⾮平衡热⼒学分⽀。⾮平衡热⼒学专⻔研究某些不处于热⼒学平衡中的物理系统,其中最为典型的研究案例是⼀滴墨⽔在⽔中扩散的过程。在扩散开始之前,这滴墨⽔会在⽔中的某个地⽅形成⼀个⼤的斑点,我们可以认为这是这滴墨⽔的初始状态,但要描述该初始状态的概率分布则很困难,因为这个概率分布⾮常复杂。随着扩散过程的进⾏,这滴墨⽔随着时间的推移逐步扩散到⽔中,⽔的颜⾊也逐渐变成这滴墨⽔的颜⾊,如图1-1所示。此时,墨⽔分⼦的概率分布将变得更加简单和均匀,这样我们就可以很轻松地⽤数学公式来描述其中的概率分布了。
在这种情况下,⾮平衡热⼒学就派上⽤场了,它可以描述这滴墨⽔随时间推移的扩散过程中每⼀个“时间步”(旨在将连续的时间过程离散化)状态的概率分布。若能够想到办法把这个过程反过来,就可以从简单的分布中逐步推断出复杂的分布。
公认最早的扩散模型DDPM(Denoising Diffusion Probabilistic Model)的扩散原理就由此⽽来,不过仅有上述条件依然很难从简单的分布倒推出复杂的分布。DDPM还做了⼀些假设,例如假设扩散过程是⻢尔可夫过程 (即每⼀个时间步状态的概率分布仅由上⼀个时间步状态的概率分布加上当前时间步的⾼斯噪声得到),以及假设扩散过程的逆过程是⾼斯分布等。

图1-1 一滴墨水在水中扩散分布的示意图
DDPM的扩散过程如图1-2和1-3所示,具体分为前向过程和反向过程两部分。扩散模型是一种潜变量模型,它使用固定的马尔可夫链映射到潜在空间。该链逐步向数据中添加噪声,以获得近似后验值,其中为与x0具有相同维数的潜变量。在下面的图中,我们可以看到这样一个马尔可夫链。

图1-2 前向过程
最后,图像逐渐变为纯高斯噪声。训练扩散模型的目标是学习逆向过程,即训练。通过沿着这条链向后遍历,我们可以生成新的数据。
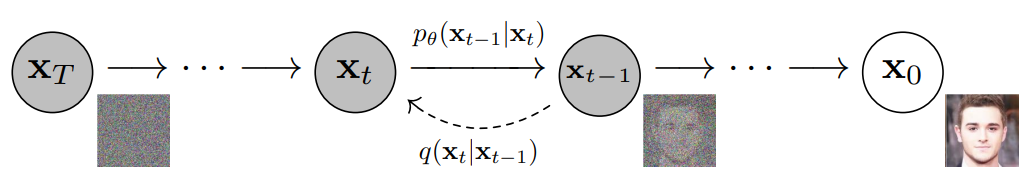
图1-3 反向过程
1)前向过程
前向过程是给数据添加噪声的过程。假设给定一批训练数据,数据分布为,其中,0表示初始,即还没有开始扩散。如前所述,将前向加噪过程分为离散的多个时间步 T ,在每一个时间步 t ,给上一个时间步t-1的数据
;添加高斯噪声,从而生成带有噪声(简称"带噪")的数据
,同时数据
,也会被送入下个时间步 t +1以继续添加噪声。其中,噪声的方差是由一个位于区间(0,1)的固定值
确定的,均值则由固定值
和当前时刻"带噪"的数据分布确定。在反复迭代和加噪(即添加噪声) T 次之后,只要 T 足够大,根据马尔可夫链的性质,最终就可以得到纯随机噪声分布的数据,即类似稳定墨水系统的状态。
接下来,我们用简单的公式描述一下上述过程。从时间步 t -1到时间步 t 的单步扩散加噪过程的数学表达式如下:
![]()
最终的噪声分布数学表达式如下:
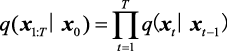
2)反向过程
前向过程是将数据噪声化的过程,反向过程则是"去噪"的过程,即从随机噪声中迭代恢复出清晰数据的过程。
要从采样自高斯噪声的一个随机噪声中恢复出原始数据
,就需要道反向过程中每一步的图像分布状态转移。类似地, DDPM 也将反向过程定义为一个马尔可夫链,只不过这个马尔可夫链是由一系列用神经网络参数化的高斯分布组成的,也就是需要训练的扩散模型。
从时间步 t 到时间步 t -1的单步反向"去噪"过程的数学表达式如下:
![]()
由于反向过程的每一步都是参数化的高斯分布,因此可以分别求高斯分布的均值和方贝叶斯公式推导的过程,最终得到时间步 t -1的高斯分布 ,的均值和方差的数学公式如下:
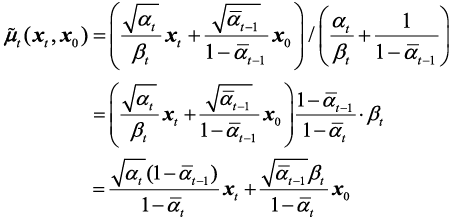
可以看出,方差是一个定量(扩散过程参数固定),而均值是一个依赖于 和
的函数,因此需要使用扩散模型来优化参数。
3)优化目标
扩散模型预测的是噪声残差,即要求后向过程中预测的噪声分布与前向过程中噪声分布的“距离”最小。
下面我们从另一个角度来看看扩散模型。如果把中间产生的变量看成隐变量的话,那么扩散模型其实是一种包含 T 个隐变量的模型,因此可以看成更深层次的 VAE ,而 VAE 的损失函数可以使用变分推断来得到变分下界( variational lower bound )。
扩散模型的最终优化目标的数学表达式如下:
![]()
可以看出,在训练 DDPM 时,只要用一个简单的 MSE ( Mean Squared Error ,均方误差)损失来最小化时向过程施加的噪声分布和后向过程预测的噪声分布,就能实现最终的优化目标。
相关文章:
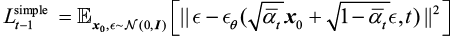
扩散模型实战(一):基本原理介绍
扩散模型(Diffusion Model)是⼀类⼗分先进的基于物理热⼒学中的扩散思想的深度学习⽣成模型,主要包括前向扩散和反向扩散两个过程。⽣成模型除了扩散模型之外,还有出现较早的VAE(Variational Auto-Encoder,…...

解决npm ERR! code ERESOLVE -npm ERR! ERESOLVE could not resolve
当使用一份vue源码开发项目时,npm install 报错了 npm ERR! code ERESOLVEnpm ERR! ERESOLVE could not resolvenpm ERR!npm ERR! While resolving: vue-admin-template4.4.0npm ERR! Found: webpack4.46.0npm ERR! node_modules/webpacknpm ERR! webpack"^4.0…...
HttpServletRequest和HttpServletResponse的获取与使用
相关笔记:【JavaWeb之Servlet】 文章目录 1、Servlet复习2、HttpServletRequest的使用3、HttpServletResponse的使用4、获取HttpServletRequest和HttpServletResponse 1、Servlet复习 Servlet是JavaWeb的三大组件之一: ServletFilter 过滤器Listener 监…...
css在线代码生成器
这里收集了许多有意思的css效果在线代码生成器适合每一位前端开发者 布局,效果类: 网格生成器https://cssgrid-generator.netlify.app/ CSS Grid Generator可帮助开发人员使用CSS Grid创建复杂的网格布局。网格布局是创建Web页面的灵活和响应式设计的强…...
在java中如何使用openOffice进行格式转换,word,excel,ppt,pdf互相转换
1.首先需要下载并安装openOffice,下载地址为: Apache OpenOffice download | SourceForge.net 2.安装后,可以测试下是否可用; 3.build.gradle中引入依赖: implementation group: com.artofsolving, name: jodconverter, version:…...
手机变电脑2023之虚拟电脑droidvm
手机这么大的内存,装个app来模拟linux,还是没问题的。 app 装好后,手指点几下确定按钮,等几分钟就能把linux桌面环境安装好。 不需要敲指令, 不需要对手机刷机, 不需要特殊权限, 不需要找驱…...

HDFS中的sequence file
sequence file序列化文件 介绍优缺点格式未压缩格式基于record压缩格式基于block压缩格式 介绍 sequence file是hadoop提供的一种二进制文件存储格式一条数据称之为record(记录),底层直接以<key, value>键值对形式序列化到文件中 优…...
【MySQL】检索数据使用数据处理函数
函数 与其他大多数计算机语言一样,SQL支持利用函数来处理数据。函数一般是在数据上执行的,它给数据的转换和处理提供了方便。 函数没有SQL的可移植性强:能运行在多个系统上的代码称为可移植的。多数SQL语句是可移植的,而函数的可…...

【嵌入式学习笔记】嵌入式入门6——定时器TIMER
1.定时器概述 1.1.软件定时原理 使用纯软件(CPU死等)的方式实现定时(延时)功能有诸多缺点,如CPU死等、延时不精准。 void delay_us(uint32_t us) {us * 72;while(us--); }1.2.定时器定时原理 使用精准的时基&#…...
GD32F103输入捕获
GD32F103输入捕获程序,经过多次测试,终于完成了。本程序将TIMER2_CH2通道映射到PB0引脚,捕获PB0引脚低电平脉冲时间宽度。PB0是一个按钮,第1次按下采集一个值保存到TIMER2_CountValue1中,第2次按下采集一个值保存到TIM…...
[RT-Thread]基于ARTPI的文件系统认识与搭建
[写作为了记忆,个人最终输出的内容往往是遗忘后最容易捡起的内容,故以此作文] 目录 [写作为了记忆,个人最终输出的内容往往是遗忘后最容易捡起的内容,故以此作文] 前提 内容 认识 基于ARTPI的文件系统的挂载 ROMFS与LFS. (默认自动挂载,romfs可读不可写) 搭…...

动态规划+二分查找
题目描述:给定一个区间数组,[[1,2,3],[3,4,2],[2,4,4]],每个区间有价值,求在获取k个区间的条件下面,求获得的最大的价值,关键是dp的定义和二分查找的写法(小于tar额最右下标) import…...

8.2小非农ADP数据来袭黄金将会如何表现?
近期有哪些消息面影响黄金走势?黄金多空该如何研判? 黄金消息面解析: 周二(8月1日)现货黄金价格回落,原因是美元指数升创7月10日以来新高至102.43.美联储官员乐观言论夯实美国经济软着陆预期。此外,中国刺激措施将…...

linux启动oracle
一、启动方法 方法1: Sql代码 cd $ORACLE_HOME/bin #进入到oracle的安装目录 ./dbstart #重启服务器 ./lsnrctl start #重启监听器 ----------------------------------- 方法2: (1) 以oracle身份登录数据库&am…...

AssetBundleBrowser导入报错解决方案
第一次导入AssetBundleBrowser遇到报错有 Assets\Scenes\AssetBundles-Browser-master\AssetBundles-Browser-master\Tests\Editor\ABModelTests.cs(13,7): error CS0246: The type or namespace name Boo could not be found (are you missing a using directive or an assem…...
vue-baidu-map-3x 使用记录
在 Vue3 TypeScript 项目中,为了采用 标签组件 的方式,使用百度地图组件,冲浪发现了一个开源库 ovo,很方便!喜欢的朋友记得帮 原作者 点下 star ~ vue-baidu-map-3xbaidu-map的vue3/vue2版本(支持v2.0、v…...
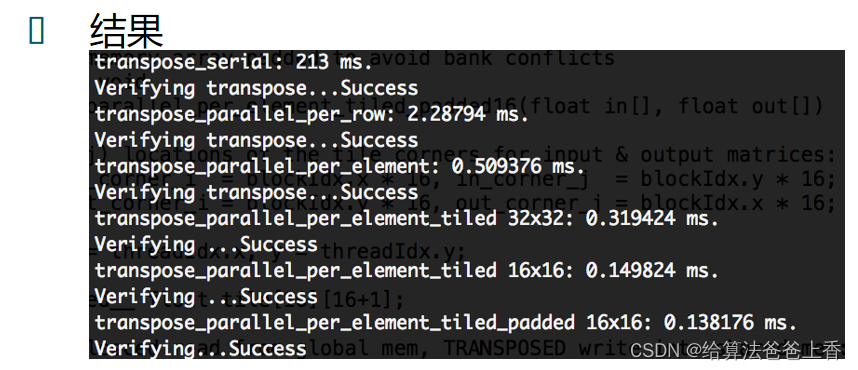
《GPU并行计算与CUDA编程》笔记
第一个GPU程序 #include <stdio.h>__global__ void square(float* d_out,float* d_in){int idx threadIdx.x;float f d_in[idx];d_out[idx] f * f; }int main(int argc,char** argv){const int ARRAY_SIZE 8;const int ARRAY_BYTES ARRAY_SIZE * sizeof(float);// …...
函数)
Shell编程基础(十二)函数
函数 概念定义调用函数综合脚本 概念 和其他编程语言一样,函数作为一种封装代码块,以提高代码复用性和可维护性的存在。 记住一点,先定义,再使用 定义 shell 函数的创建方式 function 函数名 空格{ xxxx return 返回码&#x…...

【雕爷学编程】MicroPython动手做(33)——物联网之天气预报3
天气(自然现象) 是指某一个地区距离地表较近的大气层在短时间内的具体状态。而天气现象则是指发生在大气中的各种自然现象,即某瞬时内大气中各种气象要素(如气温、气压、湿度、风、云、雾、雨、闪、雪、霜、雷、雹、霾等ÿ…...

Screens 4 for mac VNC客户端 强大的远程控制工具
Screens 4 for Mac 是一款功能强大的 VNC 客户端软件,为 Mac 用户提供了便捷的远程访问和控制解决方案。无论您是需要远程管理服务器、办公电脑,还是需要远程协助他人解决问题,Screens 4 都是您的理想选择。 Screens 4 for Mac具备简洁直观的…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
