数据结构——二叉树

本章代码仓库:堆、二叉树链式结构
文章目录
- 🍭1. 树
- 🧁1.1 树的概念
- 🧁1.2 树的结构
- 🍬2. 二叉树
- 🍫2.1 二叉树的概念
- 🍫2.2 特殊的二叉树
- 🍫2.3 二叉树的性质
- 🍫2.4 二叉树的存储结构
- 🍯3. 堆
- 🍼3.1 堆的实现
- 🥛接口声明
- 🥛接口实现
- 🍼3.2 堆排序
- 🥛堆排序实现
- 🥛堆排序时间复杂度
- ☕向下调整时间复杂度
- ☕向上调整时间复杂度
- ☕调堆时间复杂度
- 🍼3.3 Top-K
- 🍾4. 链式二叉树结构实现
- 🍷4.1 手搓链式
- 🍷4.2 二叉树遍历
- 🍻前序遍历
- 🍻中序遍历
- 🍻后序遍历
- 🍻层序遍历
- 🍷4.3 二叉树结点个数
- 🍷4.4 树的深度
- 🍷4.5 K层结点个数
- 🍷4.6 查找值为x的结点
- 🍷4.6 查找值为x的结点
🍭1. 树
🧁1.1 树的概念
树是一种非线性的数据结构,由n个有限节点组成的一个具有层次关系的有限集。
在任意一颗非空的树中:
- 有且具有一个特定的节点称为
root节点 - 除根节点外,其他节点被分成M个不互相交的有限集
- 每棵子树根节点有且仅有一个前驱节点,可以有0个或者多个后继节点
- 树是递归定义的
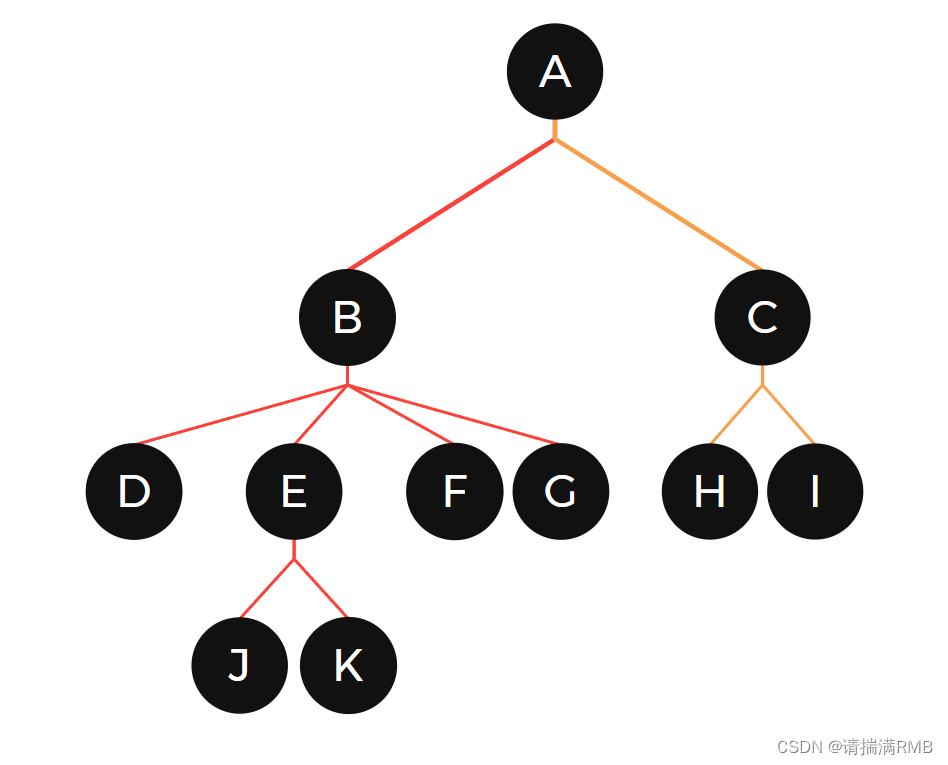
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:B的度为4
叶节点或终端节点:度为0的节点称为叶节点(没有孩子); 如上图:D、J、K、F、G、H、I
非终端节点或分支节点:度不为0的节点(有孩子); 如上图:B、C、E
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为4
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:G、H互为堂兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
🧁1.2 树的结构
树的结构如果用线性结构,就会蛮复杂,假设我们知道树的度为5,那我们就可以定义一个指针数组来表示每层的节点
#define N 5
struct TreeNode
{struct TreeNode* children[N]; //指针数组
};
在一般情况下,我们都是不知道树的度,如果采用线性结构,十分不便
struct TreeNode
{SeqList sl; //存节点指针int val;
}
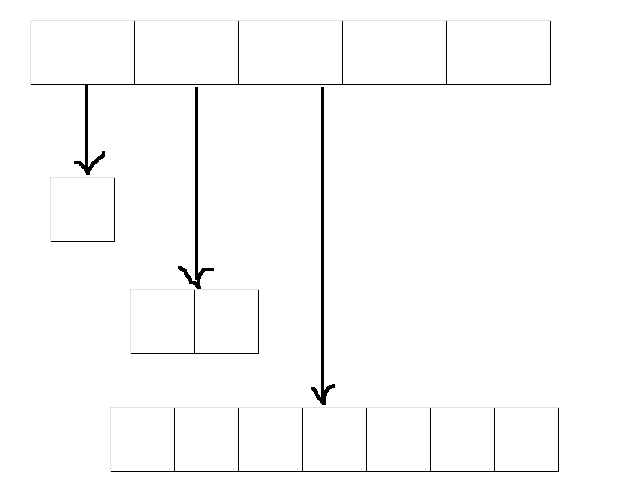
所以在实际中,一般采用孩子兄弟表示法
typedef int DateType;
struct TreeNode
{struct TreeNode* _firstChild; //第一个孩子节点struct TreeNode* _pNextBrother; //兄弟节点DateType _val; //数据
};

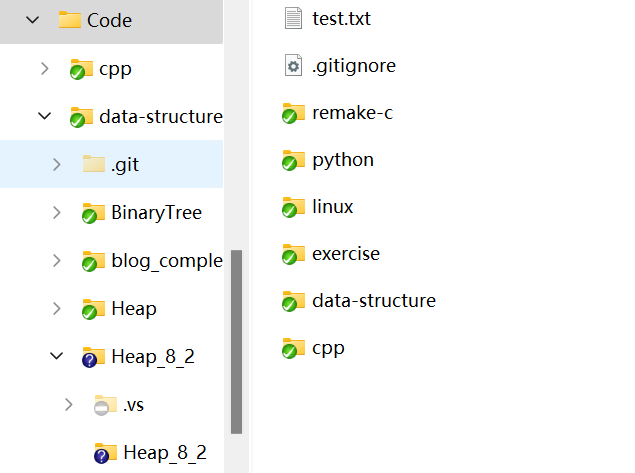
树在数据结构中并不常用,树在实际中的典型应用就是文件系统,一层一层的
将Code文件看作根节点,下面的
cpp、remake-c、linux等就能看作是它的孩子节点然后这些文件里面又包含了其他文件,层层推进
🍬2. 二叉树
🍫2.1 二叉树的概念
二叉树可以看作一个进行了“计划生育”的树
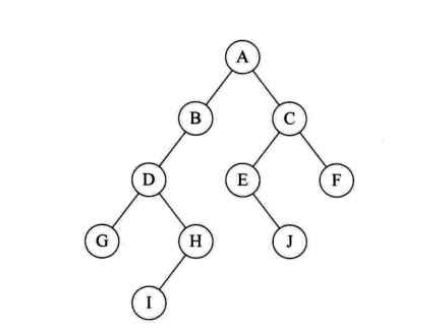
二叉树的特点:
- 每个节点至多有两颗子树(不存在度大于2的节点)
- 左子树右子树有顺序,次序不可颠倒(好比人的左右手),即使某个节点只要一棵子树,也要区分是左子树还是右子树
🍫2.2 特殊的二叉树
-
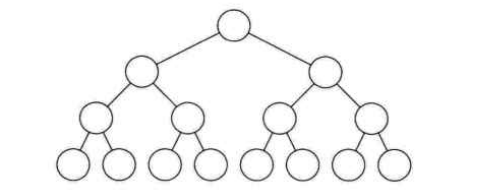
满二叉树
满二叉树就是所有的分支节点都有左右子树,并且所有叶子都在同一层
假设二叉树的深度为K,则总节点数则为2k-1
-
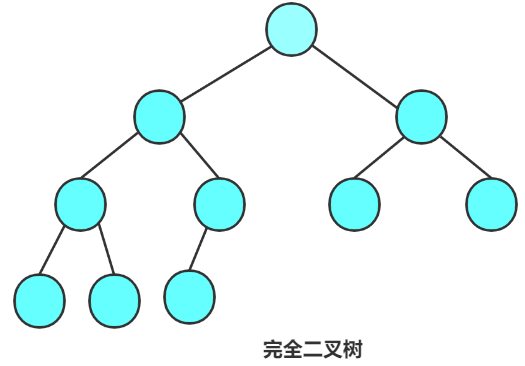
完全二叉树
完全二叉树从根节点开始,从左到右依次填充节点,直到最后一层,最后一层的节点可以不满,但节点都尽量靠左排列
满二叉树定是完全二叉树(正方形也是一种特殊的长方形)
🍫2.3 二叉树的性质
-
一颗非空二叉树第
i层至多有**2i-1**个结点 -
深度为
k的二叉树至多有2k-1 个结点 -
对于任何一颗二叉树,如果终端叶子节点为n0,度为2的结点数为n2,则n0 = n2 + 1
-
有n个结点的满二叉树的深度h = log2(n+1)
高度为h的完全二叉树,结点数量范围:[2h-1,2h-1]
-
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对 于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
🍫2.4 二叉树的存储结构
二叉树的存储结构可分为顺序存储和链式存储:
-
顺序存储
顺序存储就是用数组来存储,这一般适用于完全二叉树,因为这样不会造成空间的浪费
这在物理上是一个数组,但在逻辑上是一颗二叉树

-
链式存储
顾名思义,采用链表来表示这颗二叉树

typedef int DateType; struct TreeNode {struct TreeNode* _lChild; //左孩子struct TreeNode* _rChild; //右孩子DateType _val; //数据 };
🍯3. 堆
堆是一颗完全二叉树,堆中的每个节点都满足堆序性质,即在最大堆中,每个节点的值都大于或等于其子节点的值;在最小堆中,每个节点的值都小于或等于其子节点的值。
🍼3.1 堆的实现
下面以大根堆为例:
🥛接口声明
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
#define CAPACITY 4typedef int HPDateType;
typedef struct Heap
{HPDateType* val;int _size;int _capacity;
}HP;//初始化
void HeapInit(HP* php);
//插入数据
void HeapPush(HP* php, HPDateType x);
//删除堆顶元素
void HeapPop(HP* php);
//获取堆顶元素
HPDateType HeapTop(HP* php);
//是否有元素
bool HeapEmpty(HP* php);
//获取当前堆的元素数量
int HeapSize(HP* php);
//销毁
void HeapDestroy(HP* php);void AdjustUp(HPDateType* val, int child);
void AdjustDown(HPDateType* val, int sz, int parent);
void Swap(HPDateType* x1, HPDateType* x2);🥛接口实现
#define _CRT_SECURE_NO_WARNINGS 1
#pragma warning(disable:6031)
#include"Heap.h"//初始化
void HeapInit(HP* php)
{assert(php);php->val = (HPDateType*)malloc(sizeof(HPDateType) * CAPACITY);if (php->val == NULL){perror("malloc fail");exit(-1);}php->_size = 0;php->_capacity = CAPACITY;
}
//交换元素
void Swap(HPDateType* x1, HPDateType* x2)
{HPDateType tmp = *x1;*x1 = *x2;*x2 = tmp;
}
//向上调整 前提子树是堆
void AdjustUp(HPDateType* val, int child)
{int parent = (child - 1) / 2;while (child > 0){if (val[child] > val[parent]){Swap(&val[child], &val[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
//向下调整 前提:子树都是堆
void AdjustDown(HPDateType* val, int sz, int parent)
{//默认左孩子大int child = parent * 2 + 1;//至多叶子结点结束while (child < sz){//不越界 选出更大的孩子if (child+1<sz && val[child] < val[child+1]){child++;}if (val[child] > val[parent]){Swap(&val[child], &val[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
//插入数据
void HeapPush(HP* php, HPDateType x)
{assert(php);if (php->_size == php->_capacity){//扩容HPDateType* tmp = realloc(php->val, sizeof(HPDateType) * php->_capacity * 2);if (tmp == NULL){perror("realloc fail");exit(-1);}php->val = tmp;php->_capacity *= 2;}php->val[php->_size] = x;php->_size++;AdjustUp(php->val, php->_size - 1);
}
//删除堆顶元素
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->val[0], &php->val[php->_size - 1]);php->_size--;AdjustDown(php->val, php->_size, 0);
}
//获取堆顶元素
HPDateType HeapTop(HP* php)
{assert(php);return php->val[0];
}
//是否有元素
bool HeapEmpty(HP* php)
{assert(php);return php->_size == 0;
}
//获取当前堆的元素数量
int HeapSize(HP* php)
{assert(php);return php->_size;
}
//销毁
void HeapDestroy(HP* php)
{free(php->val);php->val = NULL;php->_size = 0;php->_capacity = 0;
}
🍼3.2 堆排序
🥛堆排序实现
堆排序分为两个步骤:
-
建堆
排升序:建大堆
排降序:建小堆
-
堆删除的思想进行排序
如果排升序,堆顶元素是最大的,将其与最后一个元素交换,这就是堆的删除操作,但我们不需要将这个数据删除,交换完不管它即可,这样最后一个元素就是最大的,然后再向下调整,再找出最大的元素,以此反复,则可完成升序的排序。
使用堆排序,不需要手搓一个数据结构堆出来,我们只需要建堆和模拟删除操作即可
//排升序 建大堆
void HeapSort(int* pa, int sz)
{//向上调整 建堆 O(N*logN)//for (int i = 0; i < sz; i++)//{// AdjustUp(pa, i);//}//向下调整 O(N)for (int i = (sz - 1 - 1) / 2; i >= 0; --i){AdjustDown(pa, sz, i);}//向下调整排序 O(N*logN)for (int i = 0; i < sz; i++){Swap(&pa[0], &pa[sz - 1 - i]);AdjustDown(pa, sz - 1 - i, 0);}}
🥛堆排序时间复杂度
建堆操作可以采用向上调整,也可以采用向下调整,但是向下调整的效率是高于向上调整的
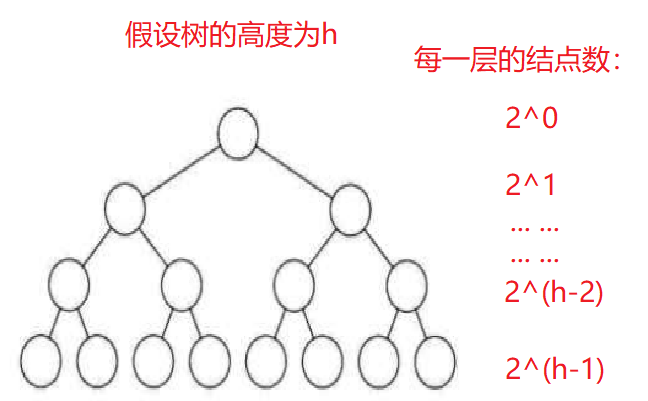
☕向下调整时间复杂度
向下调整是从第h-1层开始的
| 层数 | 结点数 | 向下移动层数 |
|---|---|---|
| 1 | 2^0 | h-1 |
| 2 | 2^1 | h-2 |
| 3 | 2^2 | h-3 |
| h-1 | 2^(h-2) | 1 |
调整次数:
T(N) = 2h-1 * 1 + 2h-2 * 2 + 2h-3 * 3 + … + 22 * (h-3) + 21 * (h-2) + 20 * (h-1)
化简得:T(N) = 2h -1 - h
高度为h的满二叉树结点个数为:N = 2h - 1
这样即可推出时间复杂度为:N - log2(N+1),N和logN不在一个量级,则时间复杂度为O(N)
过程示例:
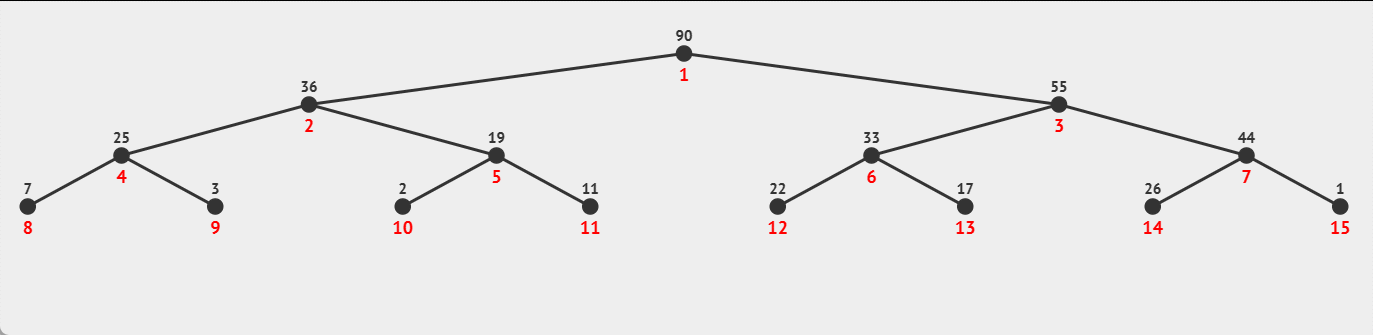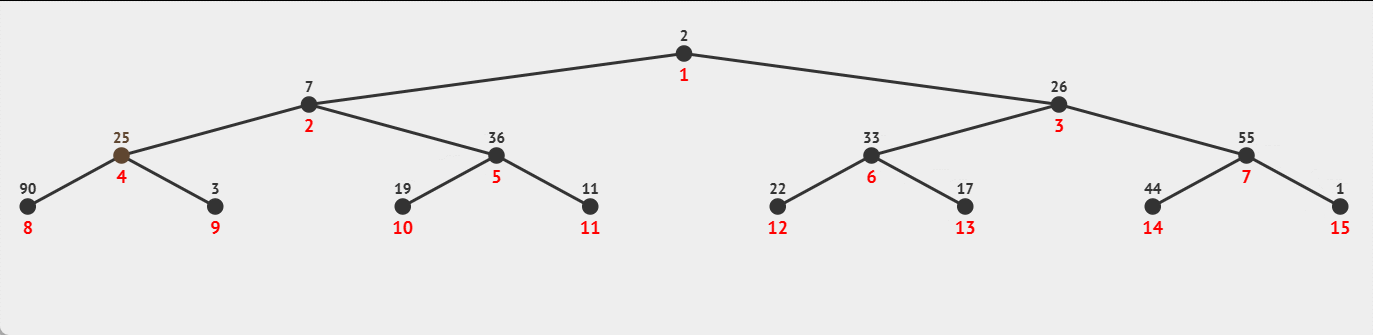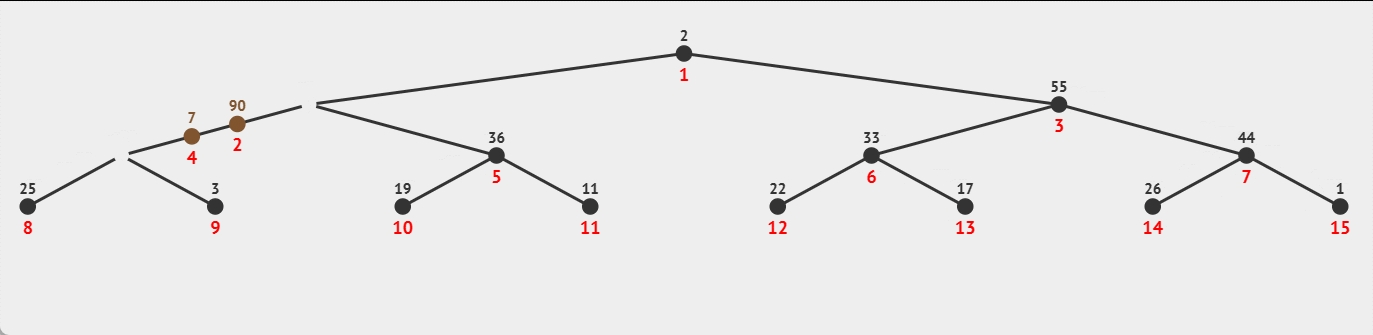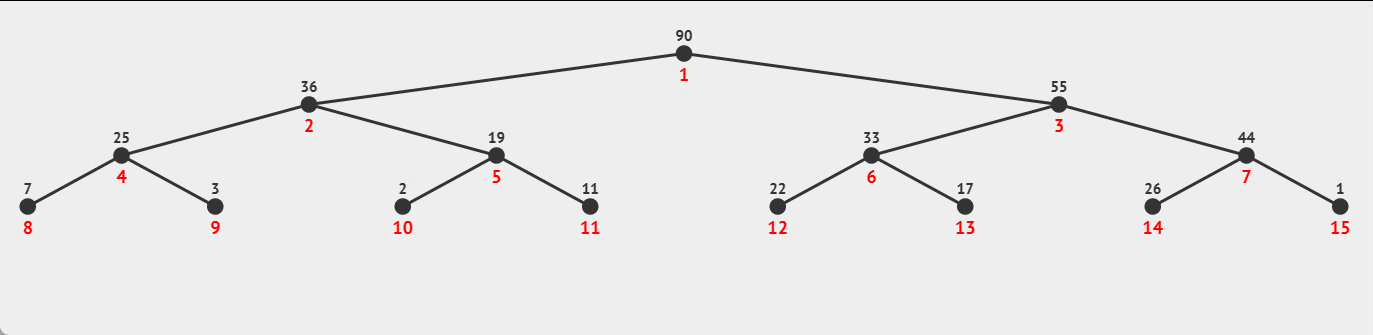
☕向上调整时间复杂度
向上调整建堆是从第二层开始调整的
| 层数 | 结点数 | 向上移动层数 |
|---|---|---|
| 2 | 2^1 | 1 |
| 3 | 2^2 | 2 |
| h-1 | 2^(h-2) | h-2 |
| h | 2^(h-1) | h-1 |
调整次数:
T(N) = 21 * 1 + 22 * 2 + … + 2h-1 * (h-2) + 2h-1 * (h-1)
化简得:T(N) = -2h + 2 + 2h * h - 2h = 2h * h - 2h * 2 + 2
高度为h的满二叉树结点个数为:N = 2h - 1
推出时间复杂度为:(N+1)*log2(N+1) - 2*(N+1) + 2,N和logN不在一个量级,则时间复杂度为O(N*logN)
过程示例:
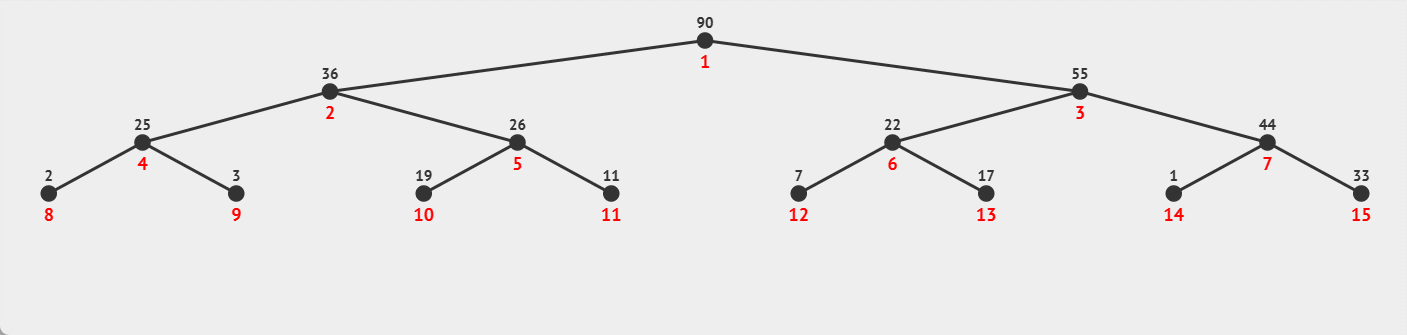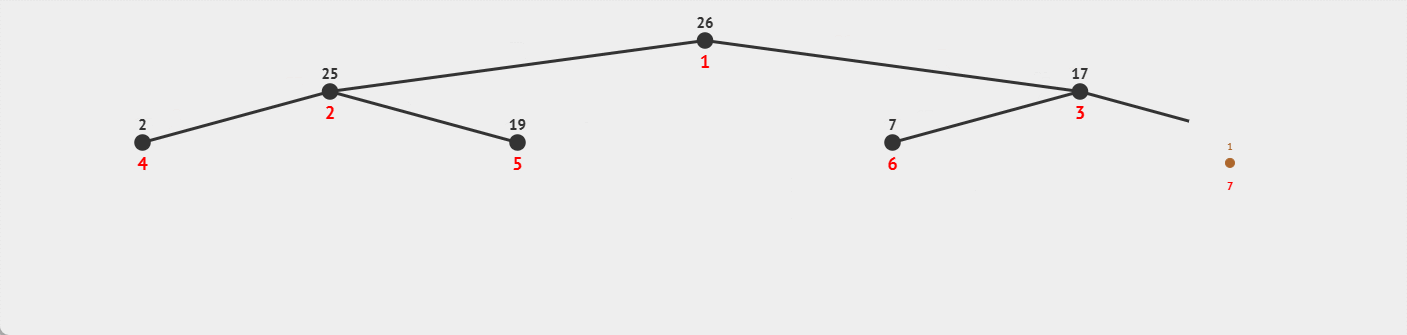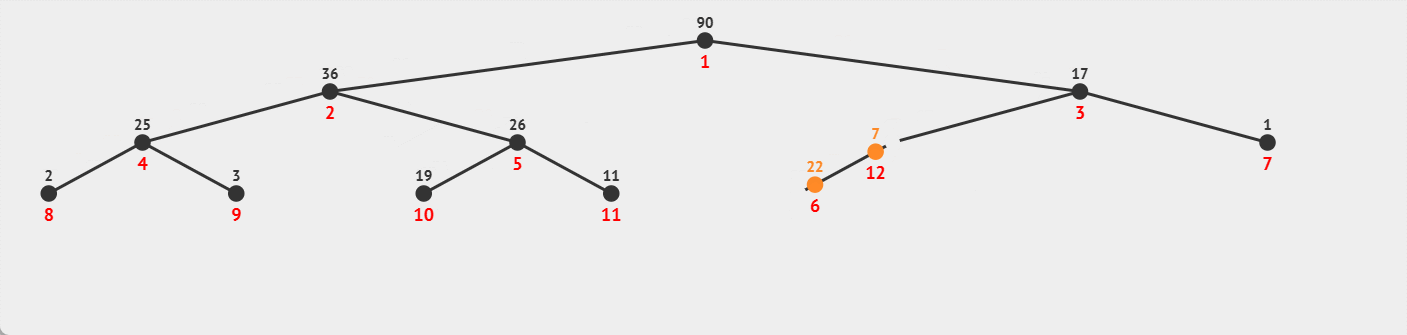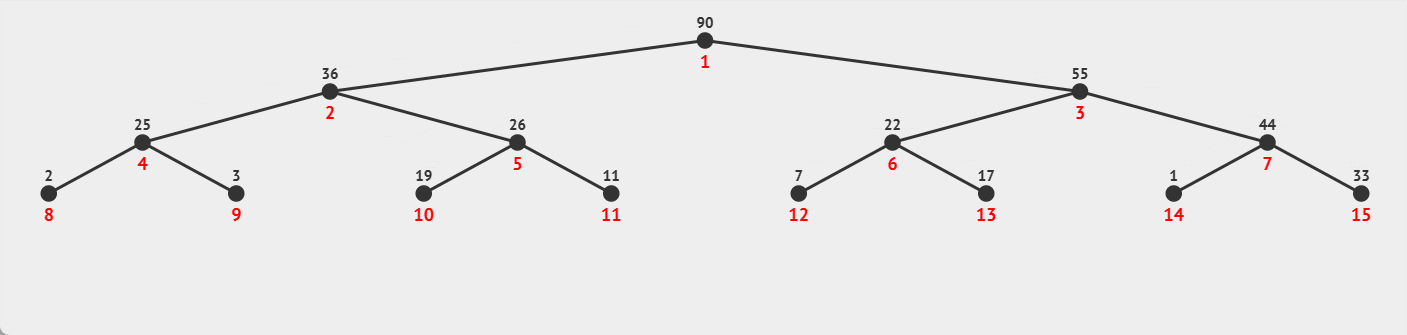
这里也很好比较:
向上调整建堆时,结点数多的地方,调整次数多;
而向下调整建堆时,结点数多的地方,调整次数少,所以采用向下调整建堆时,效率会高于向上调整
☕调堆时间复杂度
建完堆直接,我们只能保证栈顶元素是最大/最下的,要完成排序,还需要调堆
调堆采用的是删除堆顶元素的逻辑,N个元素,每次调整的时间复杂度为:O(logN),则整个堆排序时间复杂度为:N*log(N)
🍼3.3 Top-K
在现实的世界中,大部分只关注前多少多少,例如:我国排名前十的大学、一个专业学生成绩的前五等等。
这些都是排序,如果数据量较大,数据可能不会一下子就全部加载到内存当中,那我们就可以采用Top-K的思路解决:
用数据集合中的前k个来建堆,然后再用剩余的N-K个元素依次与堆顶元素比较
- 前k个最大元素,建小堆
- 前k个最小元素,建大堆
例如要在十万个数据当中找出5个最大/最小的数据,只需要建一个存储5个元素的堆
以前5个最大元素为例,那就是建小堆,那堆顶元素则是最小的,每次只需将堆顶元素和数据进行对比,如果大于堆顶元素,则替换掉堆顶元素,然后进堆,这样就一直保证,堆顶元素是这个堆中最小的元素
场景模拟:
一万个小于一万的随机数,找出前k个最大元素
void Print_TopK(const char* file, int k)
{int* topk = (int*)malloc(sizeof(int) * 5);if (topk == NULL){perror("malloc fail");exit(-1);}FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen fail");exit(-1);}//读取前k个数据for (int i = 0; i < k; i++){fscanf(fout, "%d", &topk[i]);}//建小堆for (int i = (k - 2) / 2; i >= 0; i--){AdjustDown(topk, k, i);}//将剩余元素与堆顶元素比较,大于堆顶元素则替换int val = 0;int ret = fscanf(fout, "%d", &val);while (ret != EOF){if (val > topk[0]){topk[0] = val;AdjustDown(topk, k, 0);}ret = fscanf(fout, "%d", &val);}for (int i = 0; i < k; i++){printf("%d ", topk[i]);}printf("\n");free(topk);topk = NULL;fclose(fout);
}
//造数据
void CreateDate()
{int n = 10000;srand((int)time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen fail");exit(-1);}for (size_t i = 0; i < n; i++){int x = rand() % 10000;fprintf(fin, "%d\n", x);}fclose(fin);
}
🍾4. 链式二叉树结构实现
🍷4.1 手搓链式
堆属于一种线性二叉树,对于链式二叉树,本次采用手搓的方式创建
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
//申请结点
BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(-1);}node->data = x;node->left = NULL;node->right = NULL;return node;
}
//造树(手搓)
BTNode* CreatTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);BTNode* node7 = BuyNode(7);BTNode* node8 = BuyNode(8);node1->left = node2;node1->right = node4;;node2->left = node3;node3->right = node7;node7->left = node8;node4->left = node5;node4->right = node6;return node1;
}
🍷4.2 二叉树遍历
🍻前序遍历
前序遍历也叫做先序遍历,访问顺序:根 -> 左子树 -> 右子树
//前序遍历:根 左子树 右子树
void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}
🍻中序遍历
中序遍历访问顺序:左子树 -> 根 -> 右子树
//中序遍历:左子树 根 右子树
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
🍻后序遍历
后序遍历访问顺序:左子树 -> 右子树 -> 根
//后序遍历:左子树 右子树 根
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}
🍻层序遍历
层序遍历与前三种不一样,层序遍历采用队列的方式实现:
首先根节点进队列,当遍历根节点之后,根节点出队列的同时把左右孩子带进去
然后再两个孩子依次出队,同时带入孩子的孩子,依次反复
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if(front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}QueueDestroy(&q);
}
🍷4.3 二叉树结点个数
统计左子树和右子树的结点,然后再加上自己的一个
//树的结点树
int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
🍷4.4 树的深度
这里每次都要记录每次统计的结点个数,不然每次每层都得重新统计(如:注释代码块)
//树的深度
int TreeHeight(BTNode* root)
{if (root == NULL){return 0; }//记录深度int left = TreeHeight(root->left)+1;int right = TreeHeight(root->right)+1;printf("%d %d\n", left, right);return left>right?left:right;//return root==NULL?0: TreeHeight(root->left) > TreeHeight(root->right) ? TreeHeight(root->left)+1 : TreeHeight(root->right)+1;
}
🍷4.5 K层结点个数
//K层结点个数
int TreeKLevel(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1)return 1;int leftChild = TreeKLevel(root->left, k - 1);int rightChild = TreeKLevel(root->right, k - 1);return leftChild + rightChild;}
🍷4.6 查找值为x的结点
//查找值为x的结点
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;//记录结点BTNode* leftNode = TreeFind(root->left, x);BTNode* rightNode = TreeFind(root->right, x);if (leftNode)return leftNode;else if (rightNode)return rightNode;return NULL;
}
root->left) > TreeHeight(root->right) ? TreeHeight(root->left)+1 : TreeHeight(root->right)+1;
}
## 4.5 K层结点个数```c
//K层结点个数
int TreeKLevel(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1)return 1;int leftChild = TreeKLevel(root->left, k - 1);int rightChild = TreeKLevel(root->right, k - 1);return leftChild + rightChild;}
🍷4.6 查找值为x的结点
//查找值为x的结点
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;//记录结点BTNode* leftNode = TreeFind(root->left, x);BTNode* rightNode = TreeFind(root->right, x);if (leftNode)return leftNode;else if (rightNode)return rightNode;return NULL;
}
相关文章:

数据结构——二叉树
本章代码仓库:堆、二叉树链式结构 文章目录 🍭1. 树🧁1.1 树的概念🧁1.2 树的结构 🍬2. 二叉树🍫2.1 二叉树的概念🍫2.2 特殊的二叉树🍫2.3 二叉树的性质🍫2.4 二叉树的存…...
架构训练营学习笔记:5-3接口高可用
序 架构决定系统质量上限,代码决定系统质量下限,本节课串一下常见应对措施的框架,细节不太多,侧重对于技术本质有深入了解。 接口高可用整体框架 雪崩效应:请求量超过系统处理能力后导致系统性能螺旋快速下降 链式…...

【笔记】湖仓一体架构演进与发展
https://www.bilibili.com/video/BV1oF411F7rQ/?spm_id_from333.788.recommend_more_video.0&vd_sourcefa36a95b3c3fa4f32dd400f8cabddeaf...
政务云建设与应用解决方案[42页PPT]
导读:原文《政务云建设与应用解决方案[42页PPT]》(获取来源见文尾),本文精选其中精华及架构部分,逻辑清晰、内容完整,为快速形成售前方案提供参考。 完整版领取方式 完整版领取方式: 如需获取完…...
20天突破英语四级高频词汇——第①天
20天突破英语四级高频词汇~第一天加油(ง •_•)ง💪 🐳博主:命运之光 🌈专栏:英语四级高频词汇速记 🌌博主的其他文章:点击进入博主的主页 目录 20天突破英语四级…...
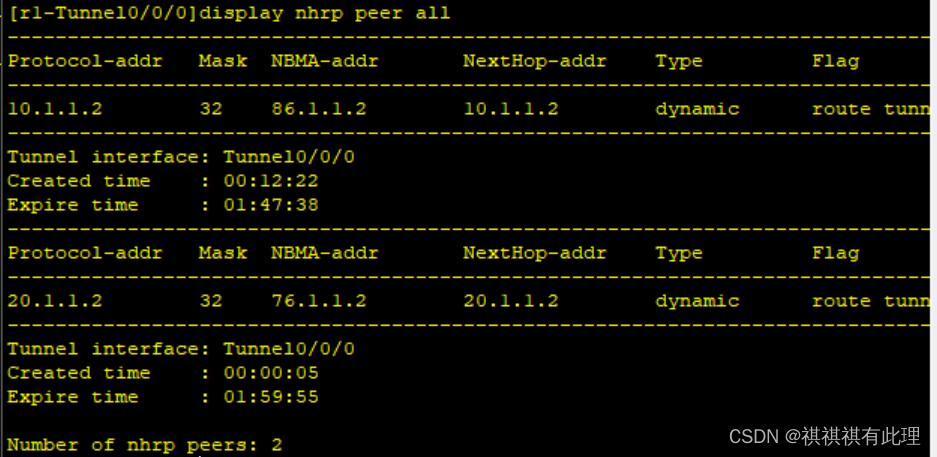
【网络基础实战之路】基于MGRE多点协议的实战详解
系列文章传送门: 【网络基础实战之路】设计网络划分的实战详解 【网络基础实战之路】一文弄懂TCP的三次握手与四次断开 【网络基础实战之路】基于MGRE多点协议的实战详解 【网络基础实战之路】基于OSPF协议建立两个MGRE网络的实验详解 PS:本要求基于…...
K8s实战入门(三)
文章目录 3. 实战入门3.1 Namespace3.1.1 测试两个不同的名称空间之间的 Pod 是否连通性 3.2 Pod3.3 Label3.4 Deployment3.5 Service 3. 实战入门 本章节将介绍如何在kubernetes集群中部署一个nginx服务,并且能够对其进行访问。 3.1 Namespace Namespace是kuber…...
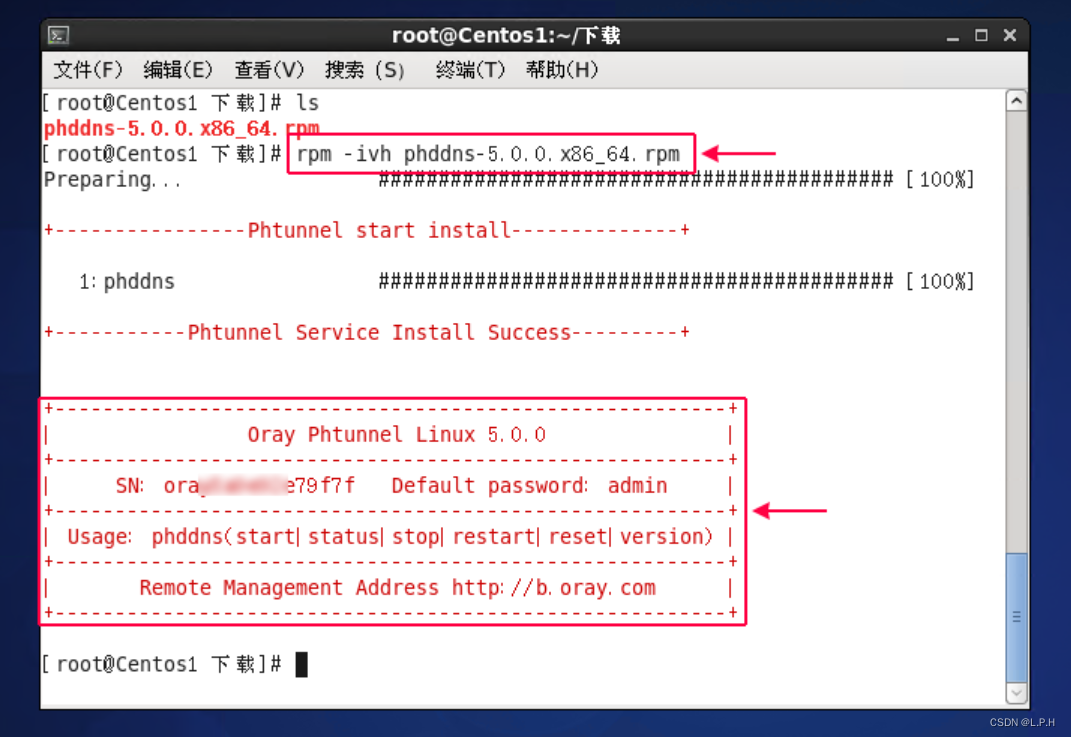
Linux-centos花生壳实现内网穿透
Linux-centos花生壳实现内网穿透 官网教程 1.安装花生壳 下载网址 点击复制就可以复制下载命令了 wget "https://dl.oray.com/hsk/linux/phddns_5.2.0_amd64.rpm" -O phddns_5.2.0_amd64.rpm# 下载完成之后会多一个rpm文件 [rootlocalhost HuaSheng]# ls phddns_…...
)
Jackson类层次结构中的一些应用(Inheritance with Jackson)
Have a look at working with class hierarchies in Jackson. 如何在Jackson中使用类层次结构。 Inclusion of Subtype Information There are two ways to add type information when serializing and deserializing data objects, namely global default typing and per-cl…...

Python求均值、方差、标准偏差SD、相对标准偏差RSD
均值 均值是统计学中最常用的统计量,用来表明资料中各观测值相对集中较多的中心位置。用于反映现象总体的一般水平,或分布的集中趋势。 import numpy as npa [2, 4, 6, 8]print(np.mean(a)) # 均值 print(np.average(a, weights[1, 2, 1, 1])) # 带…...
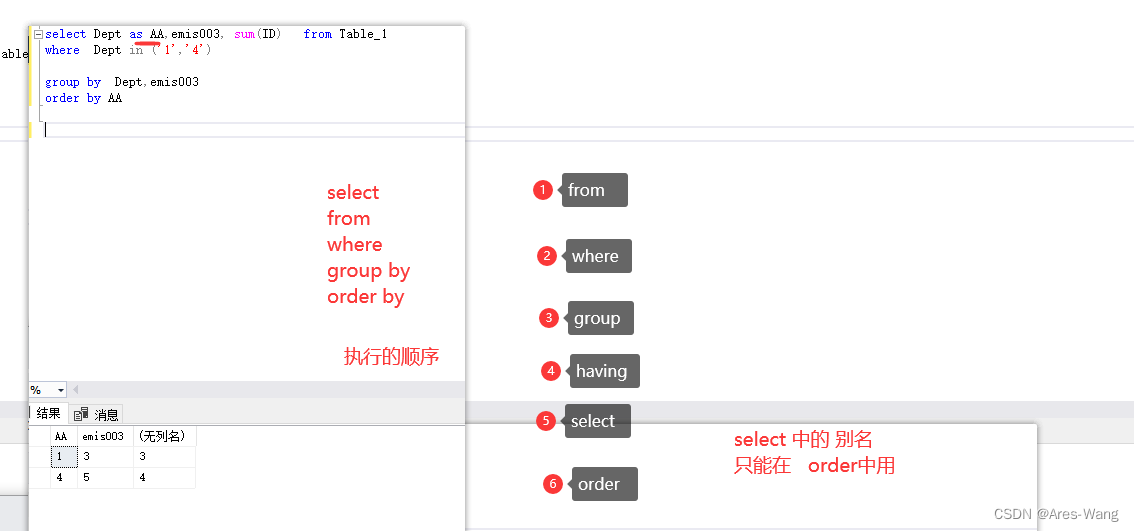
SQL ASNI where from group order 顺序
SQL语句执行顺序: from–>where–>group by -->having — >select --> order 第一步:from语句,选择要操作的表。 第二步:where语句,在from后的表中设置筛选条件,筛选出符合条件的记录。 …...
 : RestTemplate完全体)
springboot(39) : RestTemplate完全体
HTTP请求调用集成,支持GET,POST,JSON,Header调用,日志打印,请求耗时计算,设置中文编码 1.使用(注入RestTemplateService) Autowiredprivate RestTemplateService restTemplateService; 2.RestTemplate配置类 import org.springframework.context.annotation.Bean; import org.…...

python中计算2的32次方减1,python怎么算2的3次方
大家好,给大家分享一下怎么样用python编写2的n次方,n由键盘输入,很多人还不知道这一点。下面详细解释一下。现在让我们来看看! ---恢复内容开始--- 1、内置函数:取绝对值函数abs() 2、内置函数:取最大值max()ÿ…...

阿里云SLB负载均衡ALB、CLB和NLB有什么区别?
阿里云负载均衡SLB分为传统型负载均衡CLB(原SLB)、应用型负载均衡ALB和网络型负载均衡NLB,三者有什么区别?CLB是之前的传统的SLB,基于物理机架构的4层负载均衡;ALB是应用型负载均衡,7层负载均衡…...

SynergyNet(头部姿态估计 Head Pose Estimation)复现 demo测试
目录 0 相关资料1 环境搭建2 安装 SynergyNet3 下载相关文件4 编译5 测试 0 相关资料 SynergyNet(github):https://github.com/choyingw/SynergyNet 1 环境搭建 我用的AutoDL平台搭建 选择镜像 PyTorch 1.9.0 Python 3.8(ubuntu18.04) Cu…...
mysql高级(尚硅谷-夏磊)
目录 内容介绍 Linux下MySQL的安装与使用 Mysql逻辑架构 Mysql存储引擎 Sql预热 索引简介 内容介绍 1、Linux下MySQL的安装与使用 2、逻辑架构 3、sql预热 Linux下MySQL的安装与使用 1、docker安装docker run -d \-p 3309:3306 \-v /atguigu/mysql/mysql8/conf:/etc/my…...

C++实用技术(二)std::function和bind绑定器
目录 简介std::functionstd::function对象包装器std::function做回调函数 std::bind绑定器bind绑定普通函数bind绑定成员函数 简介 C11新增了std::function和std::bind。用于函数的包装以及参数的绑定。可以替代一些函数指针,回调函数的场景。 std::function std…...
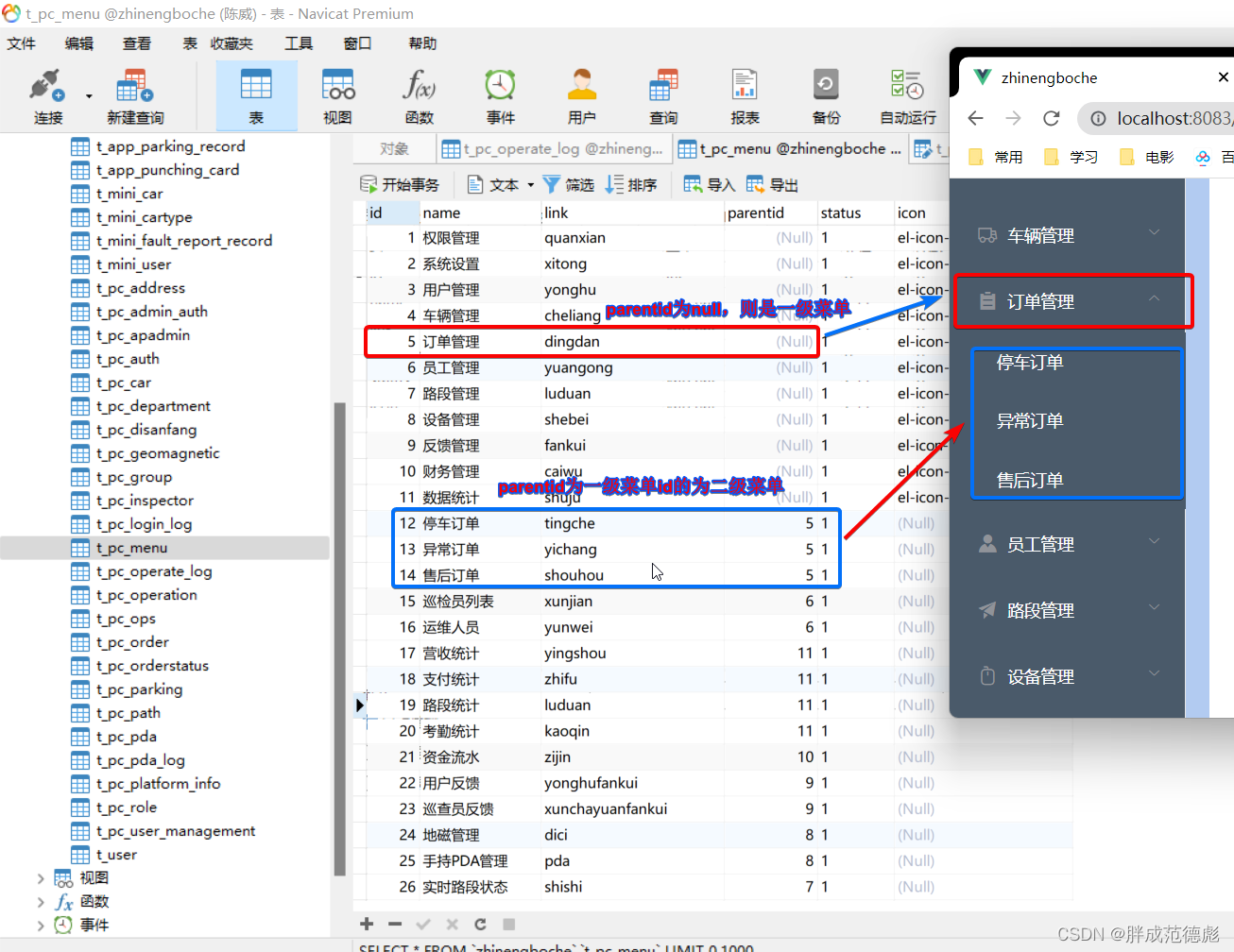
vue框架 element导航菜单el-submenu 简单使用方法--以侧边栏举例
1、目标 实现动态增删菜单栏的效果,所以要在数据库中建表 2 、建表 2.1、表样式 2.2、表数据 3、实体类 import lombok.AllArgsConstructor; import lombok.Data; import lombok.NoArgsConstructor;import java.util.List;Data AllArgsConstructor NoArgsConstr…...
Nodejs 第八章(npm搭建私服)
构建npm私服 构建私服有什么收益吗? 可以离线使用,你可以将npm私服部署到内网集群,这样离线也可以访问私有的包。提高包的安全性,使用私有的npm仓库可以更好的管理你的包,避免在使用公共的npm包的时候出现漏洞。提高…...
React Native获取手机屏幕宽高(Dimensions)
import { Dimensions } from react-nativeconsole.log(Dimensions, Dimensions.get(window)) 参考链接: https://www.reactnative.cn/docs/next/dimensions#%E6%96%B9%E6%B3%95 https://chat.xutongbao.top/...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...