判定是否互为字符重排、回文排列
题1:判定是否互为字符重排
给定两个由小写字母组成的字符串 s1 和 s2,请编写一个程序,确定其中一个字符串的字符重新排列后,能否变成另一个字符串。
输入: s1 = "abc", s2 = "bca"
输出: true
输入: s1 = "abb", s2 = "aab"
输出: false
解题思路:
1.遍历s1,构建哈希表,记录s1中出现的字符且该字符出现的个数
2. 遍历s2,在哈希表中查找s2中的字符是否在s1中出现过
若找到,同时哈希表对应的值大于1,map[s2[i]]--
若找到,同时哈希表对应的值小于1,说明当前这个字符在s2中出现的次数比s1中出现的多,返回false
若找不到,map.find(s2[i])==map.end(),说明当前字符在s1中没有出现过,返回false
源代码如下:
class Solution {
public:bool CheckPermutation(string s1, string s2) {unordered_map<char,int> map;if(s1.size()!=s2.size()) return false;for(int i=0;i<s1.size();i++){map[s1[i]]+=1;//用哈希表保存s1字符中每个字符出现的次数}for(int i=0;i<s2.size();i++){//遍历s2,找哈希表中是否存在s2字符串中的每个字符,且出现次数是否相同if(map.find(s2[i])==map.end()||map[s2[i]]<1){return false;}map[s2[i]]--;}return true;}
};题2:回文排列
给定一个字符串,编写一个函数判定其是否为某个回文串的排列之一。
回文串是指正反两个方向都一样的单词或短语。排列是指字母的重新排列。
回文串不一定是字典当中的单词。
输入:"tactcoa"
输出:true(排列有"tacocat"、"atcocta",等等)
输入:"aa"
输出:true("aa"本身就是回文串)
解题思路:
判断回文重排,也就是说判断将字符串重排后是否能够组成回文串。
这里我们定义一个sum变量,当前字符第一次出现,则sum+=1
当前字符第二次出现,则sum-=1
将所有字符遍历完后,要组成回文串
那么该字符串里每个字符出现的个数,要么都是两次,例如abba,sum=1+1-1-1=0
要么只有一个字符出现一次,其余字符都必须出现两次,例如:tacocat,sum=1+1+1+1-1-1-1=1
所以跟题1类似,我们需要判断字符出现的个数,从而判断是否是回文重排
源代码如下:
class Solution {
public:bool canPermutePalindrome(string s) {unordered_map<char,int> map;//建立哈希表来保存字符出现的次数int sum=0;//起始总和为0for(int i=0;i<s.size();i++){//在哈希表中找不到,说明是第一次出现,则sum+1//找到后,发现值为-1,说明前面已经有该字符两两配对过了,所以也就是新的一轮了则sum+1if(map.find(s[i])==map.end()||map[s[i]]==-1){map[s[i]]=1;//先给哈希表赋值sum+=map[s[i]];//sum加上当前的值}//剩下的情况就是,当前字符出现过一次,那么出现第二次时,就从sum中-1else{map[s[i]]=-1;sum+=map[s[i]];}}//只有sum=1/sum=0 才能是回文重排return sum==1||sum==0;}
};相关文章:

判定是否互为字符重排、回文排列
题1:判定是否互为字符重排 给定两个由小写字母组成的字符串 s1 和 s2,请编写一个程序,确定其中一个字符串的字符重新排列后,能否变成另一个字符串。 输入: s1 "abc", s2 "bca" 输出: true 输入: s1 &quo…...

QT QTextCharFormat 说明和使用
QTextCharFormat:设置文本编辑框字体,字号,加粗,倾斜,下划线,颜色 QTextCharFormat 类的一些常用属性和方法: setFont(const QFont &font): 设置字体。 setFontFamily(const QString &a…...
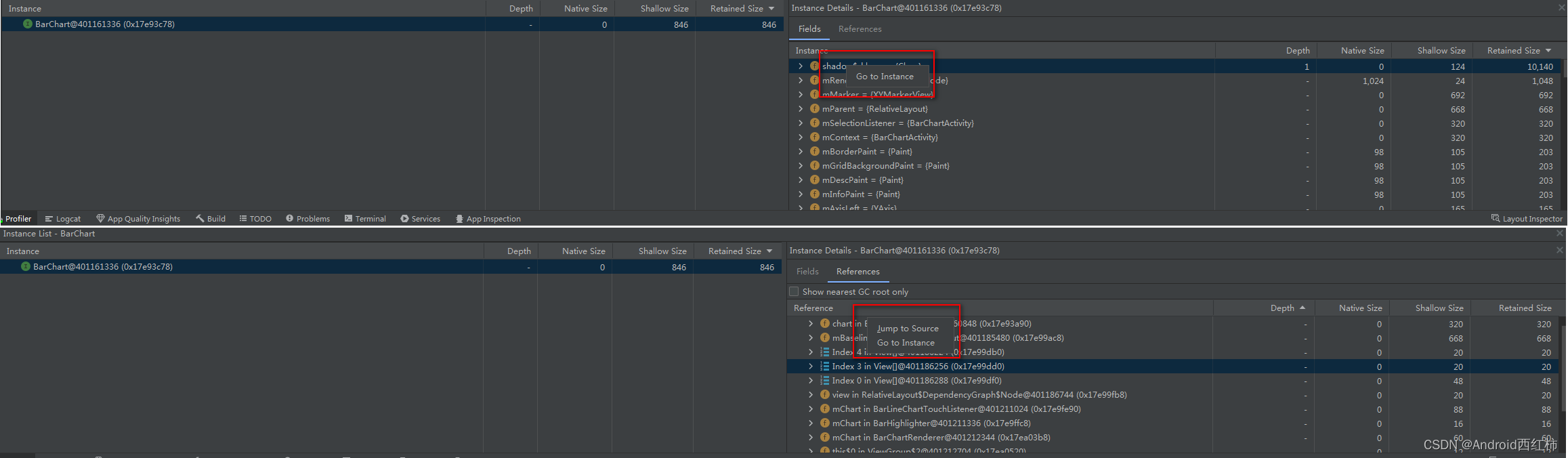
掌握Memory Profiler技巧:识别内存问题
关于作者:CSDN内容合伙人、技术专家, 从零开始做日活千万级APP。 专注于分享各领域原创系列文章 ,擅长java后端、移动开发、人工智能等,希望大家多多支持。 目录 一、导读二、概览三、如何使用四、页面说明4.1 Java 和 Kotlin 分配…...

Linux学习之正则表达式元字符和grep命令
cat /etc/redhat-release看到操作系统的版本是CentOS Linux release 7.6.1810 (Core),uname -r可以看到内核版本是3.10.0-957.21.3.el7.x86_64。 正则表达式是一种搜索字符串的模式,通俗点理解,也就是普通字符和元字符共同组成的字符集合匹…...

熟练掌握ChatGPT解决复杂问题——学会提问
目录 引言 一、5W1H分析法 1. 简单的问题(what、where、when、who) 2.复杂的问题(why、how) 2.1 为什么(Why)——原因 2.2 方式 (How)——如何 二、如何提问得到更高质量的答案…...
JVM之类加载与字节码
1.类文件结构 一个简单的HelloWorld.Java package cn.itcast.jvm.t5; // HelloWorld 示例 public class HelloWorld { public static void main(String[] args) { System.out.println("hello world"); } }编译为 HelloWorld.class 后的样子如下所示: […...

【博客688】如何实现keepalived vip监控与告警
如何实现keepalived vip监控与告警 1、使用的exporter https://github.com/mehdy/keepalived-exporter2、metrics里的状态的具体含义 注意:存状态的字符串的每个状态的值其实是跟状态在数组中的索引相对应的 具体参考这里: https://github.com/mehdy…...

[QT编程系列-39]:用户界面UI - 样式表QSS与样式文件快速入门
目录 1. 概述 2. CSS 3. QSS示例 4. QT样式表文件使用方法与步骤 5. QT内置样式 6. QT常见基本样式 1. 概述 Qt提供了一种称为Qt样式表(Qt Style Sheets)的机制,可以用于自定义和美化Qt应用程序的用户界面(UI)。…...
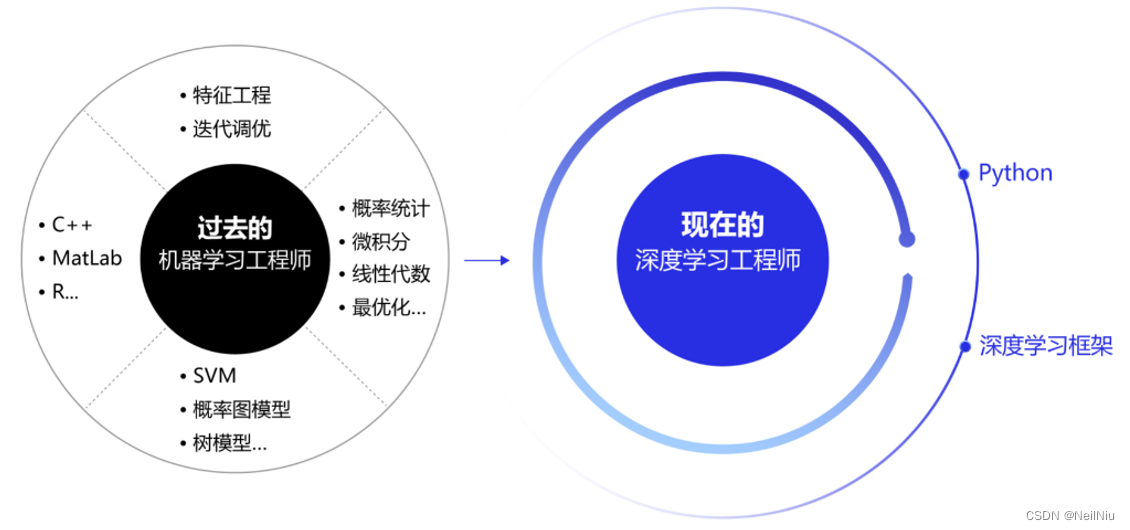
机器学习和深度学习简述
一、人工智能、机器学习、深度学习的关系 近些年人工智能、机器学习和深度学习的概念十分火热,但很多从业者却很难说清它们之间的关系,外行人更是雾里看花。概括来说,人工智能、机器学习和深度学习覆盖的技术范畴是逐层递减的,三…...
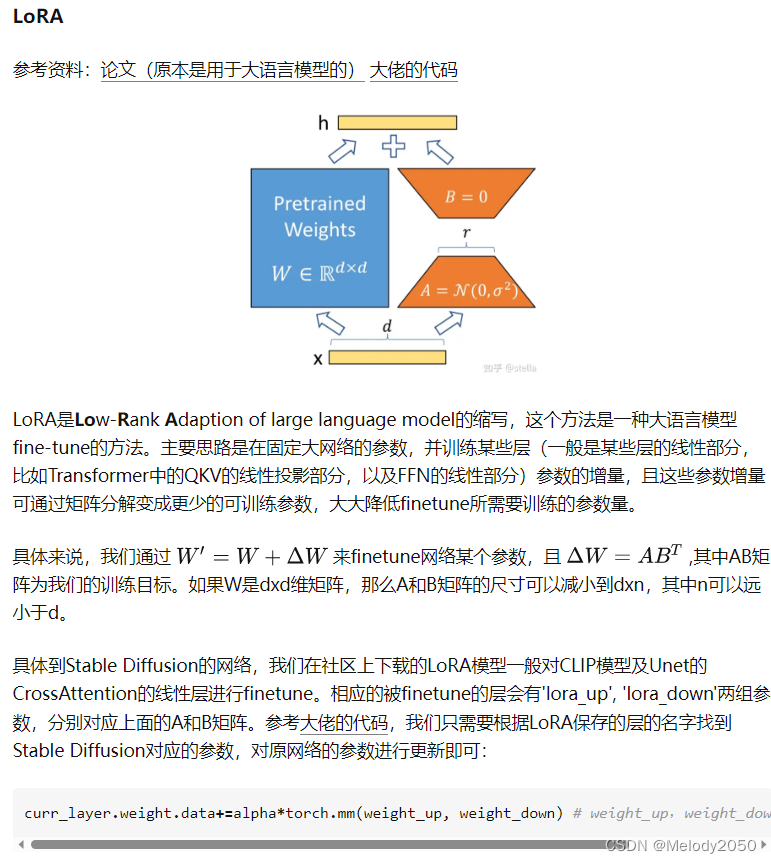
diffusion model2 扩散模型的文本信息融合、交叉注意力机制、lora
前言 在上一篇文章中,我们剖析了diffusion model的原理,而在这一篇文章中,我们探讨与扩散模型有关的其他话题,包括扩散模型的unet是如何在推理噪声的过程中,融入文本信息的考量?其原理为交叉注意力机制&am…...
数据结构——二叉树
本章代码仓库:堆、二叉树链式结构 文章目录 🍭1. 树🧁1.1 树的概念🧁1.2 树的结构 🍬2. 二叉树🍫2.1 二叉树的概念🍫2.2 特殊的二叉树🍫2.3 二叉树的性质🍫2.4 二叉树的存…...
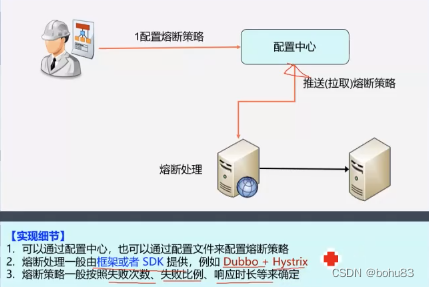
架构训练营学习笔记:5-3接口高可用
序 架构决定系统质量上限,代码决定系统质量下限,本节课串一下常见应对措施的框架,细节不太多,侧重对于技术本质有深入了解。 接口高可用整体框架 雪崩效应:请求量超过系统处理能力后导致系统性能螺旋快速下降 链式…...

【笔记】湖仓一体架构演进与发展
https://www.bilibili.com/video/BV1oF411F7rQ/?spm_id_from333.788.recommend_more_video.0&vd_sourcefa36a95b3c3fa4f32dd400f8cabddeaf...
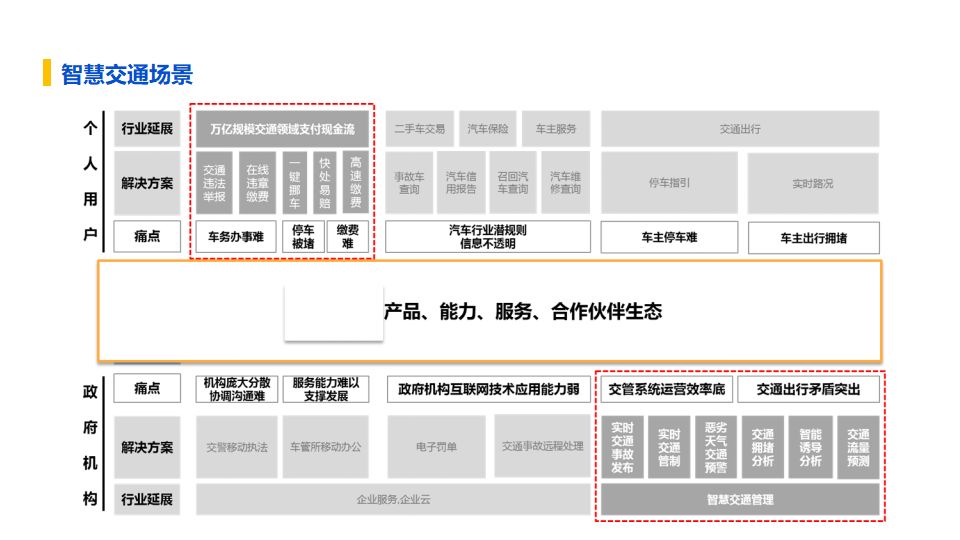
政务云建设与应用解决方案[42页PPT]
导读:原文《政务云建设与应用解决方案[42页PPT]》(获取来源见文尾),本文精选其中精华及架构部分,逻辑清晰、内容完整,为快速形成售前方案提供参考。 完整版领取方式 完整版领取方式: 如需获取完…...
20天突破英语四级高频词汇——第①天
20天突破英语四级高频词汇~第一天加油(ง •_•)ง💪 🐳博主:命运之光 🌈专栏:英语四级高频词汇速记 🌌博主的其他文章:点击进入博主的主页 目录 20天突破英语四级…...
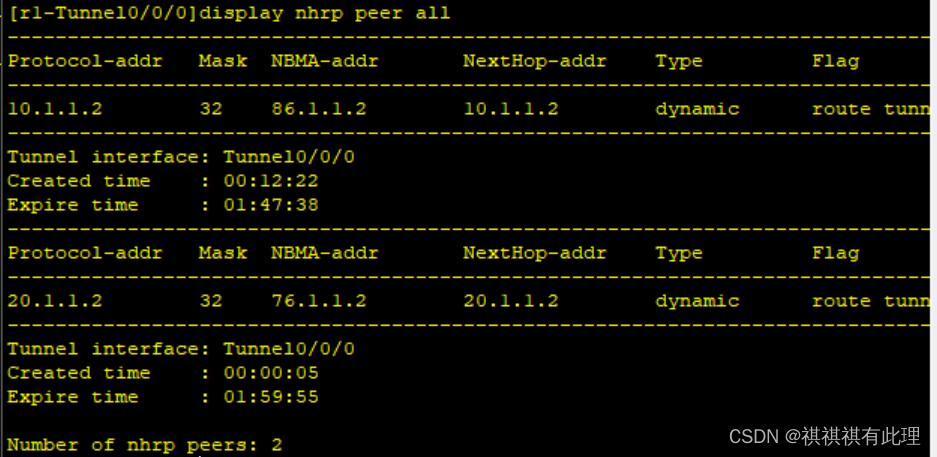
【网络基础实战之路】基于MGRE多点协议的实战详解
系列文章传送门: 【网络基础实战之路】设计网络划分的实战详解 【网络基础实战之路】一文弄懂TCP的三次握手与四次断开 【网络基础实战之路】基于MGRE多点协议的实战详解 【网络基础实战之路】基于OSPF协议建立两个MGRE网络的实验详解 PS:本要求基于…...
K8s实战入门(三)
文章目录 3. 实战入门3.1 Namespace3.1.1 测试两个不同的名称空间之间的 Pod 是否连通性 3.2 Pod3.3 Label3.4 Deployment3.5 Service 3. 实战入门 本章节将介绍如何在kubernetes集群中部署一个nginx服务,并且能够对其进行访问。 3.1 Namespace Namespace是kuber…...
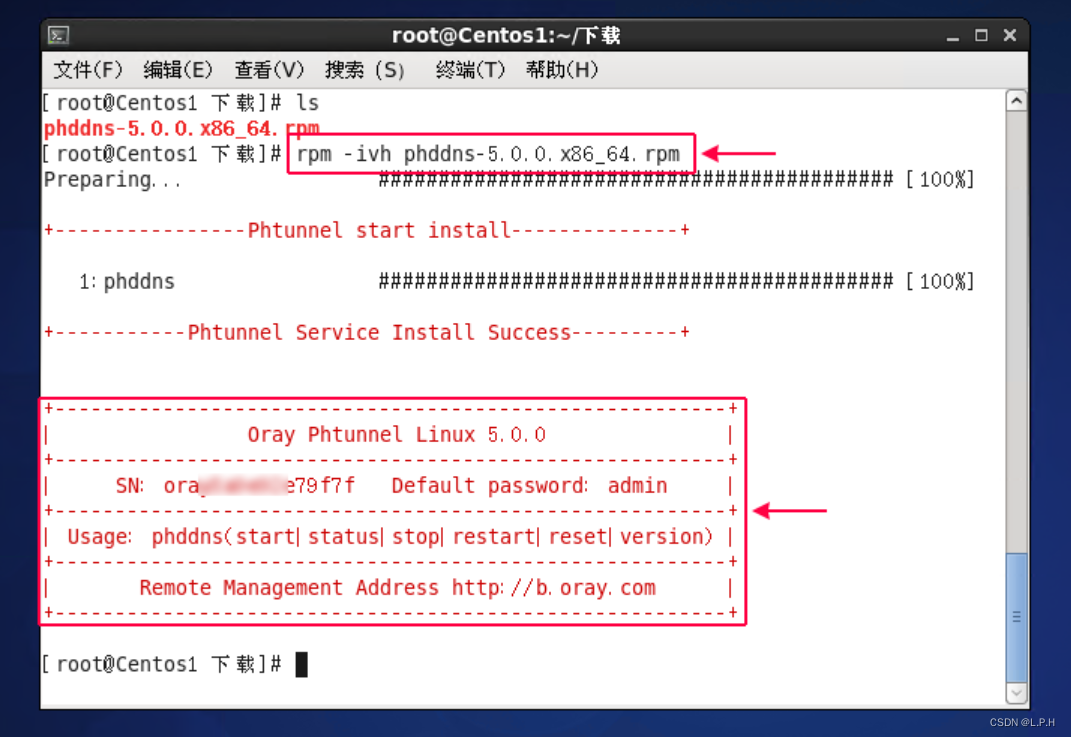
Linux-centos花生壳实现内网穿透
Linux-centos花生壳实现内网穿透 官网教程 1.安装花生壳 下载网址 点击复制就可以复制下载命令了 wget "https://dl.oray.com/hsk/linux/phddns_5.2.0_amd64.rpm" -O phddns_5.2.0_amd64.rpm# 下载完成之后会多一个rpm文件 [rootlocalhost HuaSheng]# ls phddns_…...
)
Jackson类层次结构中的一些应用(Inheritance with Jackson)
Have a look at working with class hierarchies in Jackson. 如何在Jackson中使用类层次结构。 Inclusion of Subtype Information There are two ways to add type information when serializing and deserializing data objects, namely global default typing and per-cl…...

Python求均值、方差、标准偏差SD、相对标准偏差RSD
均值 均值是统计学中最常用的统计量,用来表明资料中各观测值相对集中较多的中心位置。用于反映现象总体的一般水平,或分布的集中趋势。 import numpy as npa [2, 4, 6, 8]print(np.mean(a)) # 均值 print(np.average(a, weights[1, 2, 1, 1])) # 带…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...
