Matlab的信号频谱分析——FFT变换
Matlab的信号频谱分析——FFT变换
Matlab的信号频谱分析
FFT是离散傅立叶变换的快速算法,可以将一个时域信号变换到频域。
有些信号在时域上是很难看出什么特征的。但是如果变换到频域之后,就很容易看出特征了。
这就是很多信号分析采用FFT变换的原因。
另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
通俗点说FFT就是将一个信号解析成是由不同频率、幅值,相位的正弦波叠加而成的。
FFT变换的步骤:
1、对模拟信号离散化
一个模拟信号,经过ADC采样之后,就变成了离散的数字信号。
2、采样频率(Fs)的选取
根据采样定理,采样频率需大于信号频率的两倍。
3、采样点数( N )的选取
在FFT变换中,输入N个采样点,就有N个变换结果,每个结果都是一个复数。
每个结果都和上面所说的一个正弦信号的频率、幅值,相位对应。
复数的幅值和正弦信号的幅值对应,相位和相位对应。
而其频率的对应关系为:假设第n个结果,则其对应的频率为 Fn = (n-1)*Fs/N 。
Fs/N为分辨率,例如采样频率Fs为1024Hz,采样点数为1024点,
则每个结果以1HZ的频率步长递增。如果采样频率Fs为1024Hz,采样点数为2048点,
则每个结果以0.5HZ的频率步长递增。我们讲其分辨率为0.5HZ。
如果要提高频率分辨力,则必须增加采样点数,也即采样时间。
频率分辨率和采样时间是倒数关系。
注意:为了方便进行FFT运算,通常N取2的整数次方。
例:假设我们有一个信号,它含有一个2V的直流分量,一个频率为50Hz、相位为-30度、幅度为3V的交流信号,以及一个频率为75Hz、相位为90度、幅度为1.5V的交流信号。
用数学表达式就是如下:S=2+3cos(2pi50t-pi30/180)+1.5cos(2pi75t+pi90/180)。
我们以256Hz的采样率对这个信号进行采样,总共采样256点。
按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是1Hz,第n个点的频率就是n-1。我们的信号有3个频率:0Hz、50Hz、75Hz,应该分别在第1个点、第51个点、第76个点上出现峰值,其它各点应该接近0。
实际情况如何呢?我们来看看FFT的结果:
% 假设我们有一个信号,它含有一个2V的直流分量,一个频率为50Hz、相位为-30度、幅度为3V的交流信号,
% 以及一个频率为75Hz、相位为90度、幅度为1.5V的交流信号。
% 用数学表达式就是如下:S=2+3cos(2pi50t-pi30/180)+1.5cos(2pi75t+pi90/180)。
% 我们以256Hz的采样率对这个信号进行采样,总共采样256点。
% 按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是1Hz,
% 第n个点的频率就是n-1。
% 我们的信号有3个频率:0Hz、50Hz、75Hz,应该分别在第1个点、第51个点、第76个点上出现峰值,
% 其它各点应该接近0。
% 实际情况如何呢?我们来看看FFT的结果:clc; clear; close all;t = 0:1/255:1; %采样步长
% s1 = 2; % 一个2V的直流
% s2 = 3*cos(2*pi*50*t-pi*30/180); % 一个频率为50Hz、相位为-30度、幅度为3V的交流信号
% s3 = 1.5*cos(2*pi*75*t+pi*90/180); % 一个频率为75Hz、相位为90度、幅度为1.5V的交流信号
y = 2 + 3*cos(2*pi*50*t-pi*30/180) + 1.5*cos(2*pi*75*t+pi*90/180); % 信号叠加
N = length(t); %样点个数
plot(t,y);
xlabel('时间/s'); ylabel('幅值');
title('时域信号time domain signal');
% 采样
fs = 255; %采样频率
df = fs/(N-1); %分辨率
Y = fft(y(1:N)); %真实的幅值
figure(2)
plot((1:N/2),abs(Y(1:N/2))); %由于傅里叶算法转换得到的是对称图,而常用的只需要一半就可以了。
xlabel('Hz'); ylabel('幅值');
title('幅频响应');
%
% FFT结果的幅值和信号真实幅值对应的关系:除第一个点外,
% FFT结果的其他点的幅值是真实信号幅值N/2倍,而第一个点是真实值的N倍。
%
% FFT结果的相位和真实信号相位对比:由于是第51个点对应的是50Hz,有个错位关系,
% 还有就是FFT的幅值和真实值也有个转换关系,下面我们通过算法让其完全对应起来。
% f = (0:N-1)*df; %其中每点的频率,第一个点对应的频率为0
Y1 = fft(y(1:N))/(N/2); %真实的幅值
figure(3)
plot(f(1:N/2),abs(Y1(1:N/2))); %由于傅里叶算法转换得到的是对称图,而常用的只需要一半就可以了.
xlabel('Hz'); ylabel('幅值');
title('幅频响应');



相关文章:

Matlab的信号频谱分析——FFT变换
Matlab的信号频谱分析——FFT变换 Matlab的信号频谱分析 FFT是离散傅立叶变换的快速算法,可以将一个时域信号变换到频域。 有些信号在时域上是很难看出什么特征的。但是如果变换到频域之后,就很容易看出特征了。 这就是很多信号分析采用FFT变换的原因…...
如何从 Android 设备恢复已删除的文件?
从 Android 设备恢复已删除的文件很简单,但您需要了解内部恢复和SD 卡恢复之间的区别。 目前销售的大多数 Android 设备都配备了 SD 卡插槽(通常为 microSD),可以轻松添加额外的存储空间。该存储空间可用于存储照片、视频、文档&a…...
servlet生命周期和初始化参数传递
servlet生命周期和初始化参数传递 1、servlet生命周期 只有第一次访问才会初始化,之后访问都只执行service中的。 除非tomcat关闭重新启动: 2、初始化参数传递...

dvwa靶场通关(十一)
第十一关:Reflected Cross Site Scripting (XSS) low 这一关没有任何防护,直接输入弹窗 <script>alert(xss)</script> 打开网页源代码, 从源代码中我们可以看到,前面是输出的第一部分Hello,我们输入的脚…...
【Spring】使用注解存储Bean对象
目录 一、配置扫描路径(使用注解的方式存对象的前提) 二、使用类注解存储Bean对象 1、使用五大类注解存储Bean对象 2、为什么要这么多的类注解? 2.1、五大类注解之间的关系 3、获取Bean对象时的默认命名规则 三、使用方法注解来存储…...

怎么维护好自己的电脑
你的电脑已经成为你工作、学习、娱乐的最佳工具之一,但是如果你不做好电脑维护工作,就可能面临着电脑变慢、蓝屏、崩溃等问题。在这篇文章中,我们将介绍10个电脑维护步骤,让你的电脑更加稳定! 为什么需要电脑维护&…...
vscode中无法使用git解决方案
1 首先查看git安装目录 where git 2 找到bash.exe 的路径 比如:C:/Users/Wangzd/AppData/Local/Programs/Git/bin/bash 3 找到vscode的配置项setting.json 4 添加 "terminal.integrated.shell.windowns": "C:/Users/Wangzd/AppData/Local/Pr…...

MybatisPlus-CRUD,不带条件构造器的常用方法
mapper层 Repository public interface UserMapper extends BaseMapper<User> BaseMapper中封装好了增删改查的方法 后面直接调用就好了 测试类 SpringBootTest public class CrudTest {Autowiredprivate UserMapper userMapper;//新增Testpublic void insert(){//没…...

软件测试面试【富途面经分享】
目录 一面面经(1h) 二面面经 一面面经(1h) 一、对白盒黑盒灰盒测试的理解 答: 1、黑盒测试就当整个程序是个黑盒子,我们看不到它里面做了什么事情,只能通过输入输出看是否能得到我们所需的来…...
antd 库的 Table 组件中删除一个或多个选中的列表
先解释一下原代码每个方法的含义 const TablePage: React.FC () > {/* selectedRowKeys 指定选中项的 key 数组,需要和 onChange 进行配合在此处,通过 rowSelection.selectedRowKeys 来控制选中项。*/const [selectedRowKeys, setSelectedRowKeys] …...
针对java程序员的了解细节操作系统与进程
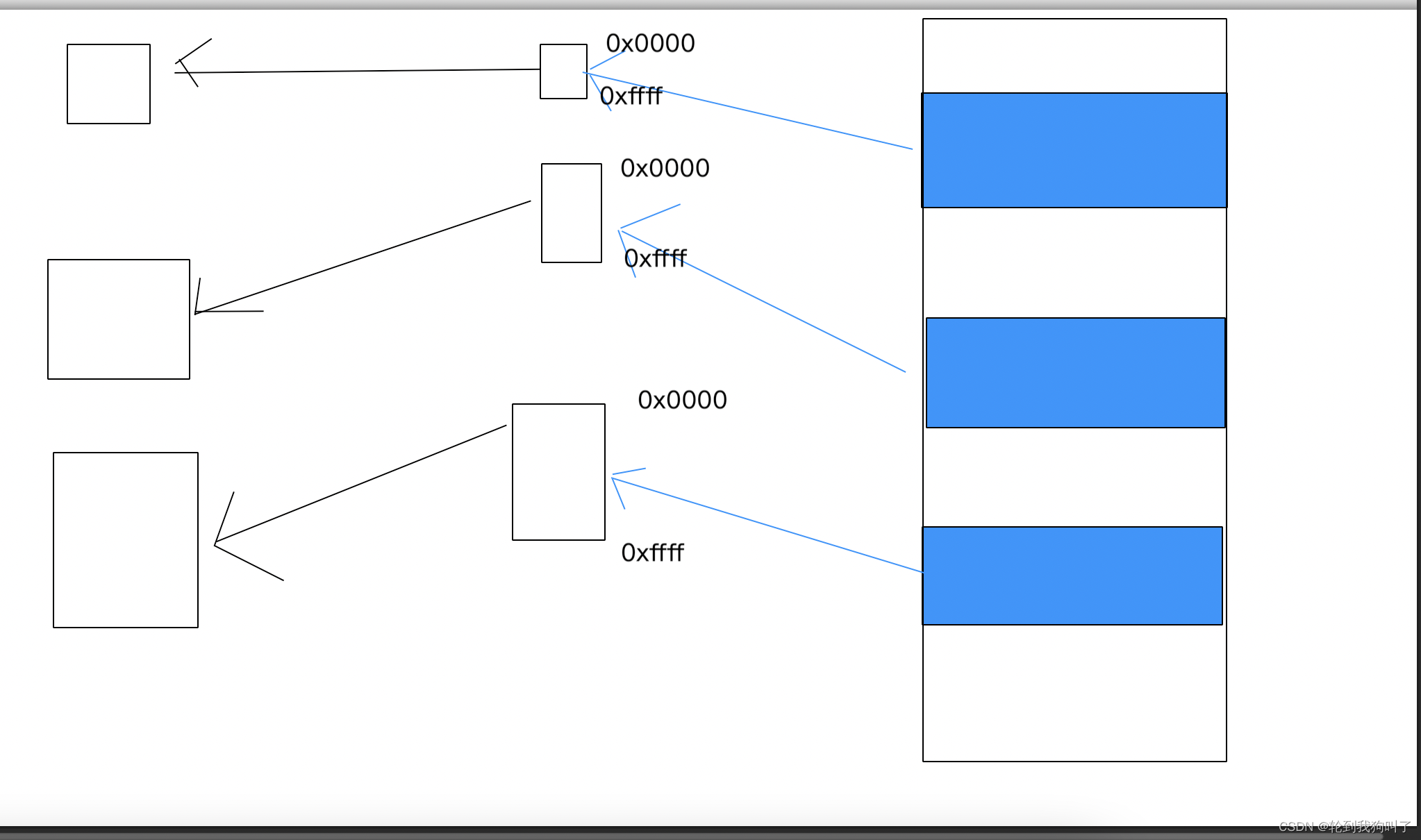
一、💛 操作系统(浅浅概念):是用来搞管理软件的 1.对下,要管理各种硬件设备 2.对上,要给应用程序提供一个稳定的运行环境 二、💙 进程:正在运行的程序,假如程序没有运行就不叫程序,…...

判定是否互为字符重排、回文排列
题1:判定是否互为字符重排 给定两个由小写字母组成的字符串 s1 和 s2,请编写一个程序,确定其中一个字符串的字符重新排列后,能否变成另一个字符串。 输入: s1 "abc", s2 "bca" 输出: true 输入: s1 &quo…...

QT QTextCharFormat 说明和使用
QTextCharFormat:设置文本编辑框字体,字号,加粗,倾斜,下划线,颜色 QTextCharFormat 类的一些常用属性和方法: setFont(const QFont &font): 设置字体。 setFontFamily(const QString &a…...
掌握Memory Profiler技巧:识别内存问题
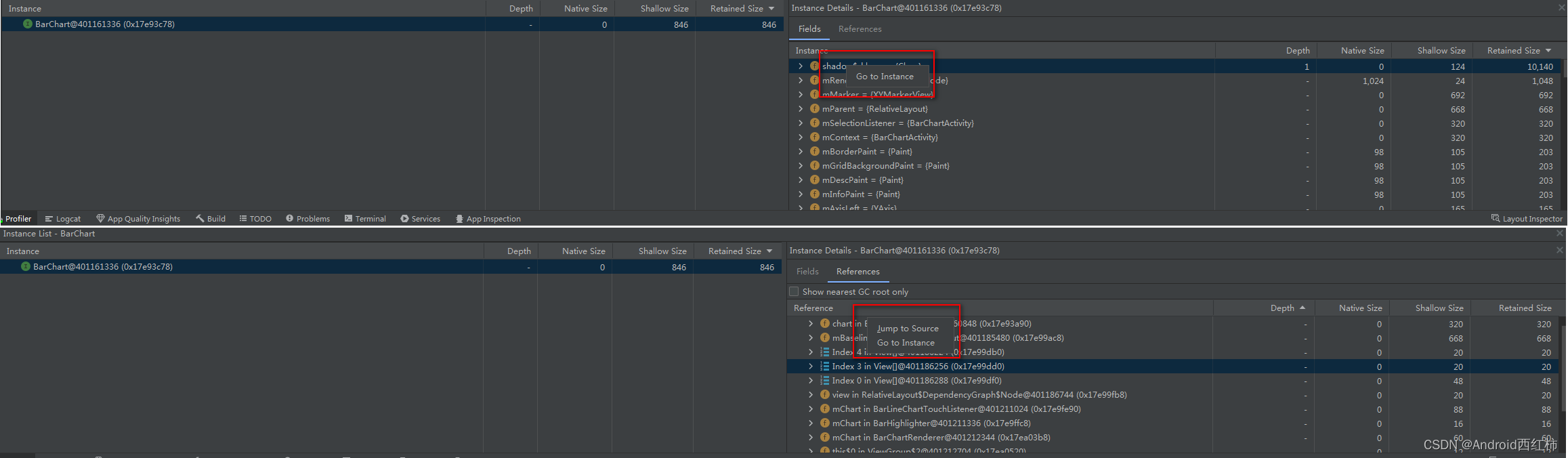
关于作者:CSDN内容合伙人、技术专家, 从零开始做日活千万级APP。 专注于分享各领域原创系列文章 ,擅长java后端、移动开发、人工智能等,希望大家多多支持。 目录 一、导读二、概览三、如何使用四、页面说明4.1 Java 和 Kotlin 分配…...

Linux学习之正则表达式元字符和grep命令
cat /etc/redhat-release看到操作系统的版本是CentOS Linux release 7.6.1810 (Core),uname -r可以看到内核版本是3.10.0-957.21.3.el7.x86_64。 正则表达式是一种搜索字符串的模式,通俗点理解,也就是普通字符和元字符共同组成的字符集合匹…...

熟练掌握ChatGPT解决复杂问题——学会提问
目录 引言 一、5W1H分析法 1. 简单的问题(what、where、when、who) 2.复杂的问题(why、how) 2.1 为什么(Why)——原因 2.2 方式 (How)——如何 二、如何提问得到更高质量的答案…...
JVM之类加载与字节码
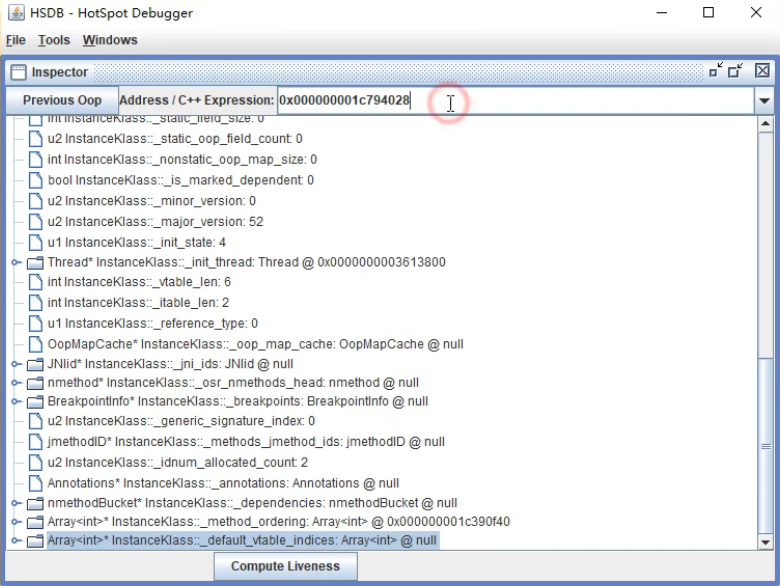
1.类文件结构 一个简单的HelloWorld.Java package cn.itcast.jvm.t5; // HelloWorld 示例 public class HelloWorld { public static void main(String[] args) { System.out.println("hello world"); } }编译为 HelloWorld.class 后的样子如下所示: […...

【博客688】如何实现keepalived vip监控与告警
如何实现keepalived vip监控与告警 1、使用的exporter https://github.com/mehdy/keepalived-exporter2、metrics里的状态的具体含义 注意:存状态的字符串的每个状态的值其实是跟状态在数组中的索引相对应的 具体参考这里: https://github.com/mehdy…...

[QT编程系列-39]:用户界面UI - 样式表QSS与样式文件快速入门
目录 1. 概述 2. CSS 3. QSS示例 4. QT样式表文件使用方法与步骤 5. QT内置样式 6. QT常见基本样式 1. 概述 Qt提供了一种称为Qt样式表(Qt Style Sheets)的机制,可以用于自定义和美化Qt应用程序的用户界面(UI)。…...
机器学习和深度学习简述
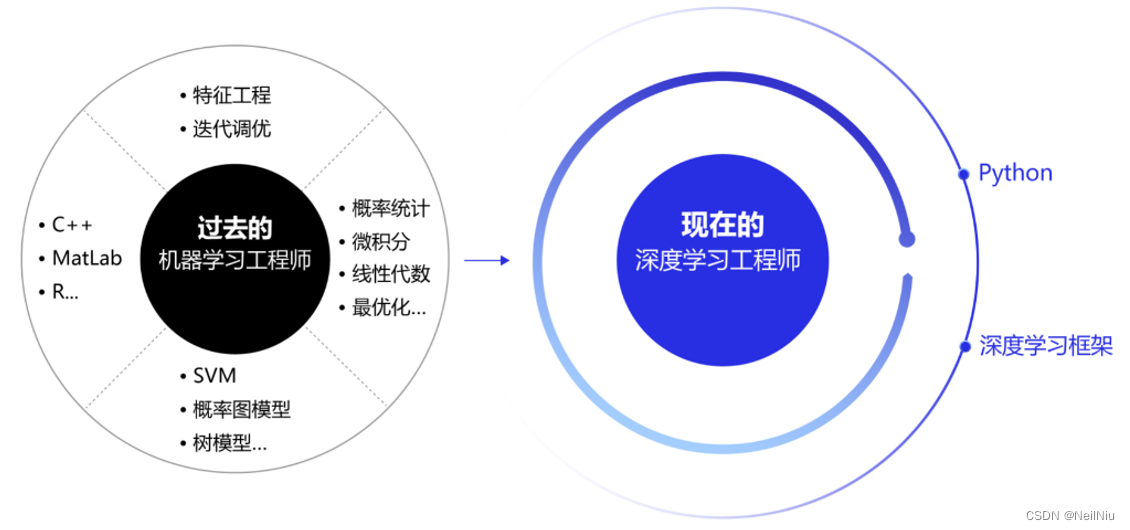
一、人工智能、机器学习、深度学习的关系 近些年人工智能、机器学习和深度学习的概念十分火热,但很多从业者却很难说清它们之间的关系,外行人更是雾里看花。概括来说,人工智能、机器学习和深度学习覆盖的技术范畴是逐层递减的,三…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
