深入探索二叉树:应用、计算和遍历
当涉及到二叉树的计算问题时,我们可以进一步介绍如何计算叶子节点数、树的宽度和叶子的深度,并解释三种常见的二叉树遍历方式:先序遍历、中序遍历和后序遍历。
1. 计算叶子节点数
叶子节点是指没有子节点的节点,也就是树中的末端节点。计算二叉树的叶子节点数,可以通过递归的方式遍历树的每个节点,如果某个节点没有左子节点和右子节点,那么它就是一个叶子节点。
以下是计算叶子节点数的示例代码:
int countLeaves(TreeNode* root) {if (root == nullptr) {return 0;} else if (root->left == nullptr && root->right == nullptr) {return 1;} else {return countLeaves(root->left) + countLeaves(root->right);}
}
2. 计算树的宽度
树的宽度是指树中某一层节点的最大数量。要计算树的宽度,我们可以使用广度优先搜索(BFS)的方法遍历树的每一层,并记录每一层的节点数量,然后找到其中最大的数量。
以下是计算树的宽度的示例代码:
int maxWidth(TreeNode* root) {if (root == nullptr) {return 0;}int max_width = 0;queue<TreeNode*> q;q.push(root);while (!q.empty()) {int level_size = q.size();max_width = max(max_width, level_size);for (int i = 0; i < level_size; ++i) {TreeNode* node = q.front();q.pop();if (node->left) {q.push(node->left);}if (node->right) {q.push(node->right);}}}return max_width;
}
3. 计算叶子的深度
叶子的深度指的是树中叶子节点所在的层数。可以通过深度优先搜索(DFS)遍历树的每个节点,并记录到达叶子节点时的层数。
以下是计算叶子的深度的示例代码:
int maxLeafDepth(TreeNode* root) {if (root == nullptr) {return 0;} else if (root->left == nullptr && root->right == nullptr) {return 1;} else {return max(maxLeafDepth(root->left), maxLeafDepth(root->right)) + 1;}
}
4. 三种常见的二叉树遍历方式
-
先序遍历(Pre-order Traversal):先序遍历是指首先访问根节点,然后按照先序遍历方式递归地访问左子树和右子树。
先序遍历的顺序是:根节点 -> 左子树 -> 右子树。
-
中序遍历(In-order Traversal):中序遍历是指先递归地访问左子树,然后访问根节点,最后递归地访问右子树。
中序遍历的顺序是:左子树 -> 根节点 -> 右子树。
-
后序遍历(Post-order Traversal):后序遍历是指先递归地访问左子树,然后递归地访问右子树,最后访问根节点。
后序遍历的顺序是:左子树 -> 右子树 -> 根节点。
5. 二叉树的计算和遍历
当计算二叉树的叶子节点数、树的宽度和叶子的深度时,我们可以用数学公式来表示。假设树的根节点为R,其左子树为L,右子树为R,用N(L)表示以L为根的子树的叶子节点数,N®表示以R为根的子树的叶子节点数。
- 先序遍历:
Pre-order® = R + Pre-order(L) + Pre-order®
- 中序遍历:
In-order® = In-order(L) + R + In-order®
- 后序遍历:
Post-order® = Post-order(L) + Post-order® + R
这些公式描述了遍历过程的顺序,其中R表示根节点,L表示左子树,R表示右子树。通过这些公式,我们可以更好地理解三种遍历方式的执行顺序。
6. 计算叶子节点数
叶子节点数 = N(L) + N® + 1
7. 计算树的宽度
树的宽度 = max(N(level1), N(level2), …, N(levelN))
其中,N(levelX)表示第X层的节点数。
8. 计算叶子的深度
叶子的深度 = max(D(L), D®) + 1
其中,D(L)表示左子树的深度,D®表示右子树的深度。
这些公式可以帮助我们在不用具体代码的情况下理解如何计算二叉树的叶子节点数、树的宽度和叶子的深度。同时,我们还可以用以下公式表示三种常见的二叉树遍历方式:
总结:通过使用数学公式来表示二叉树的计算过程,我们可以更加抽象地理解二叉树的结构和计算问题的方法。这些公式为我们提供了一种更通用、更抽象的描述方式,使我们能够更好地理解二叉树的特性和算法。
总结:二叉树作为一种重要的数据结构,它有着广泛的应用和解决方案。了解如何计算叶子节点数、树的宽度和叶子的深度,以及三种常见的遍历方式,将有助于更好地理解和应用二叉树的相关概念,解决各种与二叉树相关的计算问题。希望本文能够帮助你进一步探索二叉树的奥秘和魅力!
相关文章:

深入探索二叉树:应用、计算和遍历
当涉及到二叉树的计算问题时,我们可以进一步介绍如何计算叶子节点数、树的宽度和叶子的深度,并解释三种常见的二叉树遍历方式:先序遍历、中序遍历和后序遍历。 1. 计算叶子节点数 叶子节点是指没有子节点的节点,也就是树中的末端…...

关于 1 + 1 = 2 的证明
1 1 2 首先是皮亚诺的自然数公理 意大利数学家皮亚诺提出的关于自然数的 5 5 5 条公理如下(定义 S ( x ) S(x) S(x) 为自然数 x x x 的后继): 0 0 0 是自然数每一个自然数 n n n 都有一个自然数后继记为 S ( n ) S(n) S(n) 0 0 0 不是…...
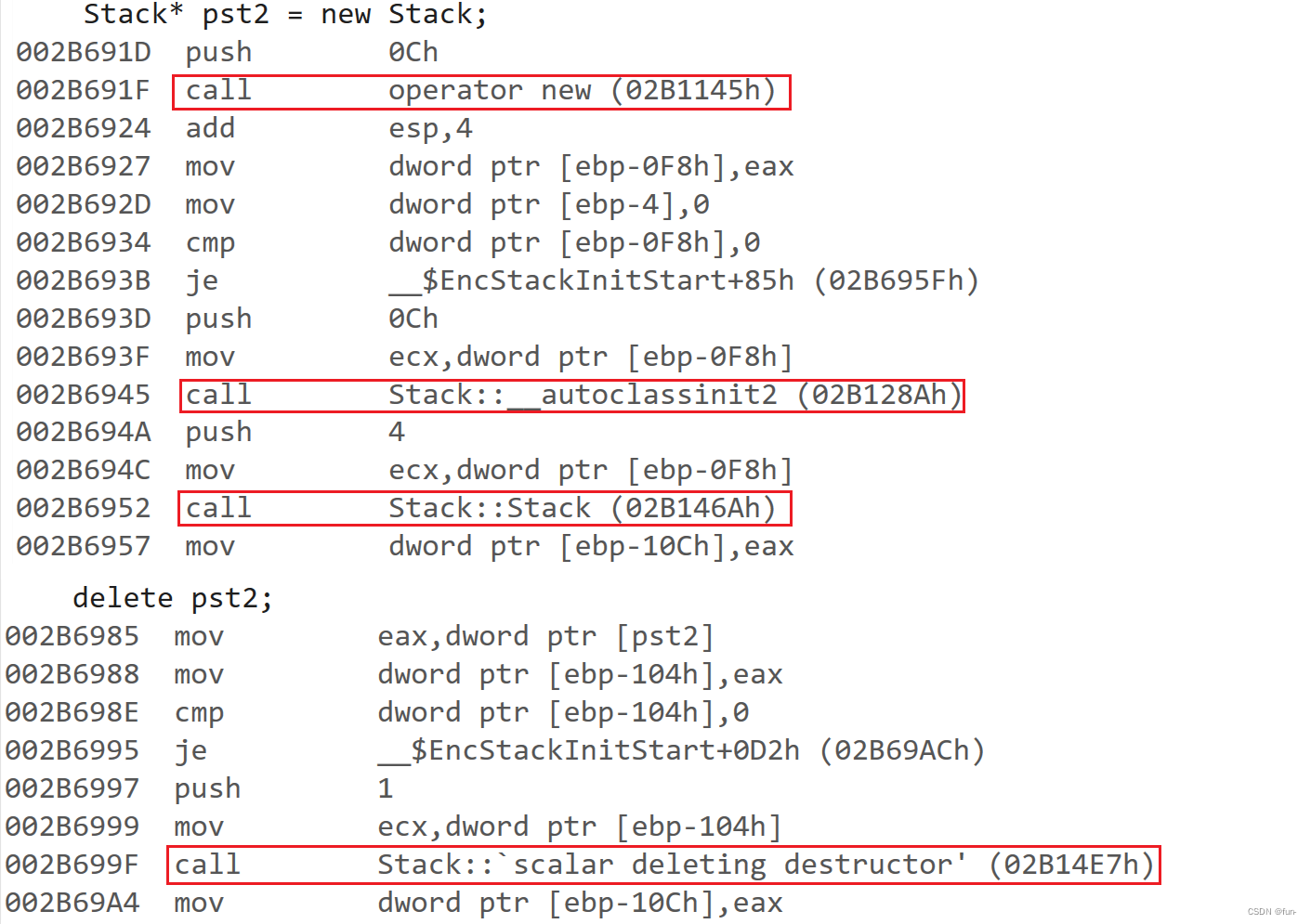
【C++】——内存管理
目录 回忆C语言内存管理C内存管理方式new deleteoperator new与operator delete函数new和delete的实现原理定位new表达式(placement-new)malloc/free和new/delete的区别 回忆C语言内存管理 void Test() {int* p1 (int*)malloc(sizeof(int));free(p1);int* p2 (int*)calloc(4…...

Jmeter录制HTTPS脚本
Jmeter录制HTTPS脚本 文章目录 添加“HTTP代理服务器”设置浏览器代理证书导入存在问题 添加“HTTP代理服务器” 设置浏览器代理 保持端口一致 证书导入 点击一下启动让jmeter自动生成证书,放在bin目录下: 打开jmeter的SSL管理器选择刚刚生成的证书&…...

Linux 的Centos 7 安装 启动 Google Chrome
我之所以在Centos上安装Chrome主要是为了让Web自动化测试工具可以启动Chrome,协助我做一些工作。 参考:centos7 google-chrome的安装与启动 - 简书 1.安装chrome逻辑 1. 下载安装包 2. 安装 3. 启动 》这就是在window上的逻辑,只是用命令行…...

DNS WEB HTTP
DNS与域名 网络是基于 TCP/IP 协议进行通信和连接的。 每一台主机都有唯一的标识,用于区别在网络上成千上万个用户和计算机。即固定的IP地址(32位二进制数转换成为十进制数——点分十进制)。每一个与网络相连接的计算机和服务器都被指派一个…...
微信小程序animation动画,微信小程序animation动画无限循环播放
需求是酱紫的: 页面顶部的喇叭通知,内容不固定,宽度不固定,就是做走马灯(轮播)效果,从左到右的走马灯(轮播),每播放一遍暂停 1500ms ~ 2000ms 刚…...

node.js
什么是Node.js Node.js 是一个免费的、开源的、跨平台的 JavaScript 运行时环境,使开发者可以搭建服务器端的JavaScript应用程序 概念: 使用Node.js编写后端程序 // 支持前端工程化 后端程序:提供接口和数据 ,网页资源 前端工程化:对代码压缩&…...
【微信小程序创作之路】- 小程序远程数据请求、获取个人信息
【微信小程序创作之路】- 小程序远程数据请求、获取个人信息 第七章 小程序远程数据请求、获取个人信息 文章目录 【微信小程序创作之路】- 小程序远程数据请求、获取个人信息前言一、远程数据请求1.本地环境2.正式域名 二、获取用户个人信息1.展示当前用户的身份信息2.获取用…...

XML基础知识讲解
文章目录 1. xml简介2. xml快速入门3. xml的元素(标签)定义4. xml标签的命名规范5. xml的属性定义和注释6. 转义字符7. CDATA区8. xml的处理指令9. xml的约束 1. xml简介 XML(eXtensible Markup Language)是一种用于描述数据的标记语。 它以纯文本的方…...
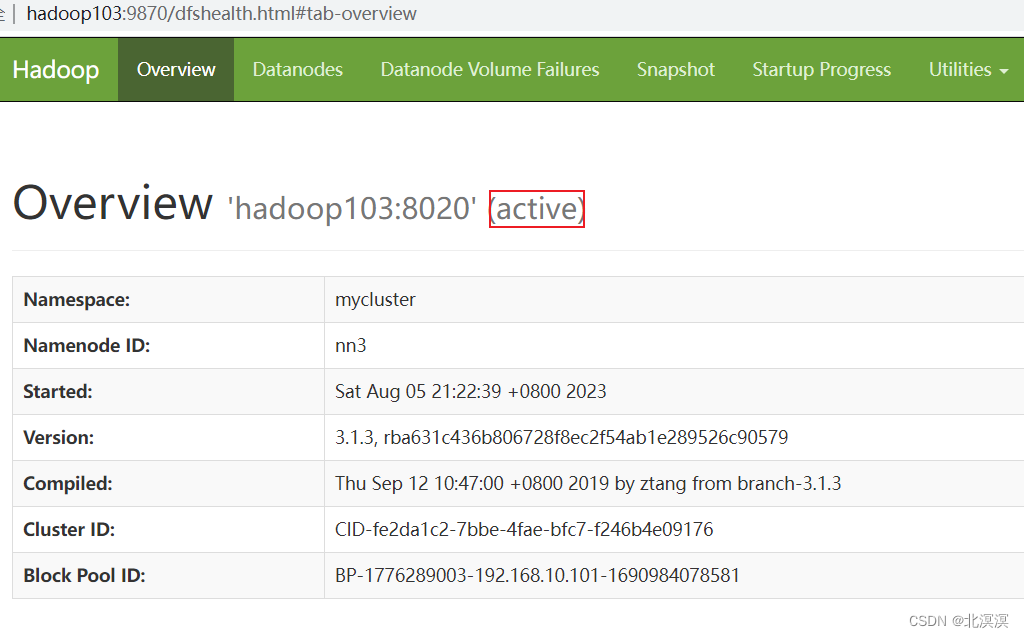
(十二)大数据实战——hadoop集群之HDFS高可用自动故障转移
前言 本节内容主要介绍一下hadoop集群下实现HDFS高可用的自动故障转移,HDFS高可用的自动故障转移主要通过zookeeper实现故障的监控和主节点的切换。自动故障转移为 HDFS 部署增加了两个新组件:ZooKeeper 和 ZKFailoverController (ZKFC&…...

Ubuntu下载deb包及其依赖包
一、简介 有时我们需要在离线环境使用提前准备好的deb包,然后只需要在新机器使用dpkg -i安装即可。 二、命令 apt-get download $(apt-rdepends (需要下载的包,可以有多个) | grep -v "^ " | sed s/debconf-2.0/debco…...

Ubuntu中解/压缩命令
一、zip文件 #解压 unzip filename.zip #压缩 zip filename.zip dirname # 递归处理,将指定目录下的所有文件和子目录一并压缩 zip -r filename.zip dirname 二、tar文件 # 解压 tar xvf FileName.tar # 压缩,将DirName和其下所有文件(夹)打包非压…...
剑指 Offer 12. 矩阵中的路径(回溯 DFS)
文章目录 题目描述思路分析完整代码 题目描述 给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。 单词必须按照字母顺序,通过相邻的单元格内的字母构成ÿ…...

iceberg对比hive优势
1.事务性 从事务性上来说,iceberg具有更高的数据质量。 因为iceberg本质是一种table format,屏蔽了底层的存储细节,写入数据时候需要严格按照schema写入。而hive可以先写入底层数据,然后使用load partition的方式来加载分区。这样…...

ProgressBar基本使用
作用:进度条,用于展示某个任务的完成情况, 常用属性: 设定进度条的最大、最小值、自增步长 常用事件: 后台代码: private void progressBar1_Click(object sender, EventArgs e){Thread t;//使用线程执行…...

spring boot java使用XEasyPdf生成pdf文档
java使用XEasyPdf生成pdf文档 spring boot java使用XEasyPdf生成pdf文档第一步导入maven坐标,pom.xml全部贴上第二步编写代码代码实战: spring boot java使用XEasyPdf生成pdf文档 第一步导入maven坐标,pom.xml全部贴上 <?xml version"1.0" encoding…...
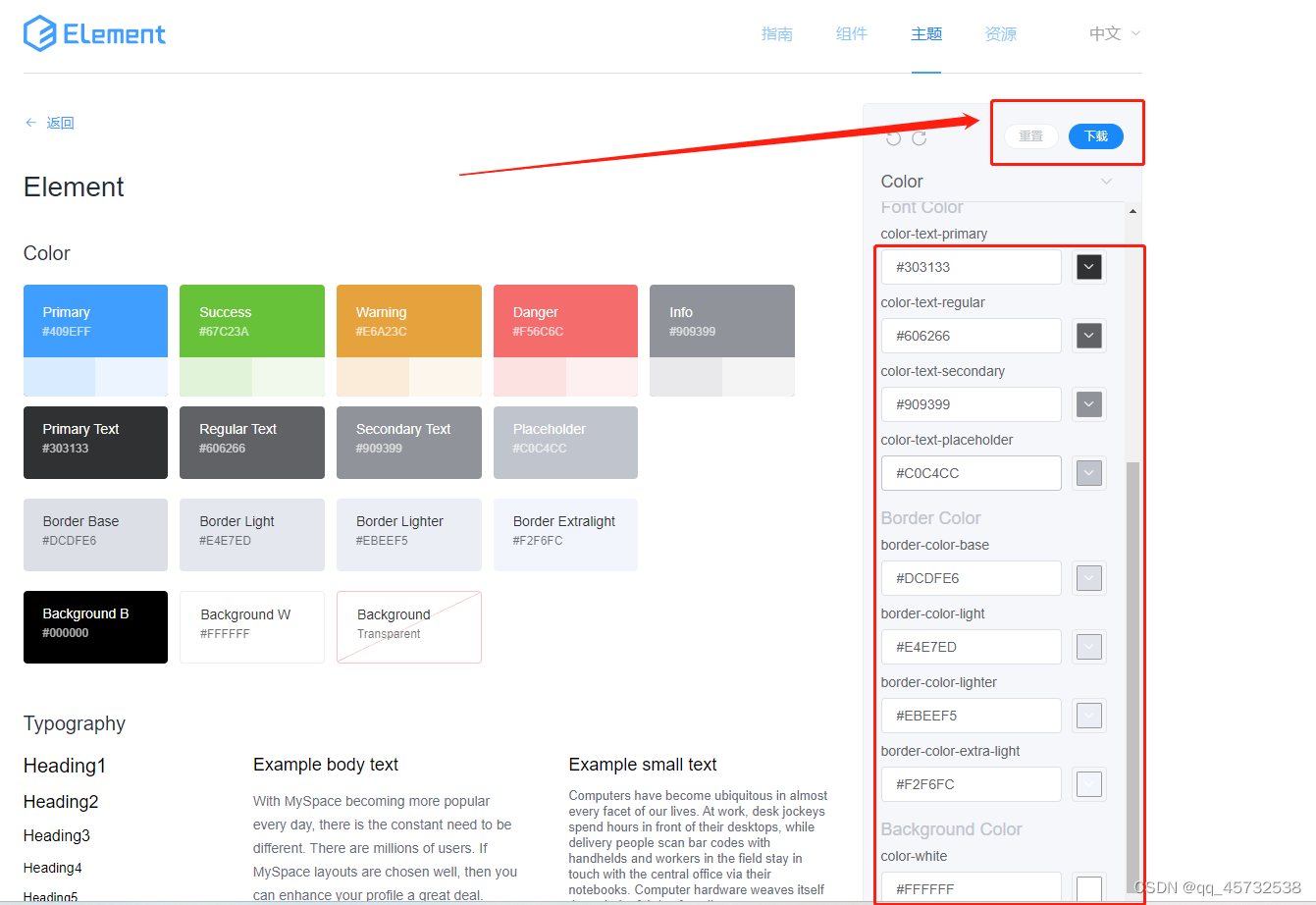
自定义elementui的主题
通常情况下,我们使用elementui框架的时候默认组件的主题都是白色的,比如: 但是如果想自定义主题,改变主题颜色,以及各种默认颜色,其实也不难: 配置默认主题,选好后点击下载 在vu…...
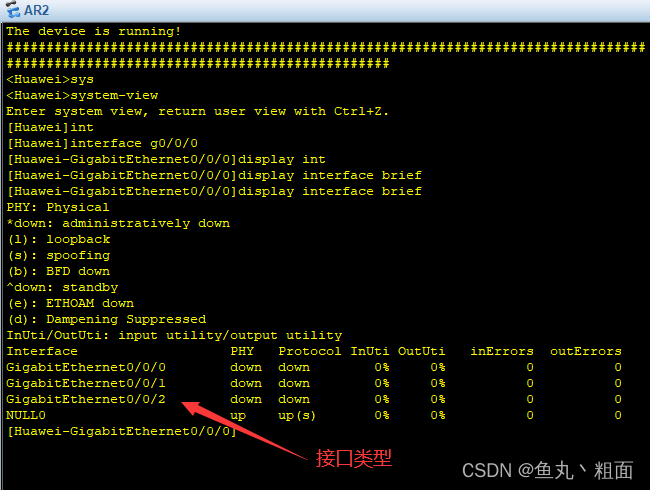
eNSP interface g0/0/0 报错解决办法
文章目录 1 报错截图2 解决办法2.1 排查设备是否有 GM 接口2.2 更换适合的路由器,并验证 1 报错截图 2 解决办法 2.1 排查设备是否有 GM 接口 查看下设备是否支持 GM 接口(GigabitEthernet) 方式一:右键路由器设备 - 设置 - 查看…...
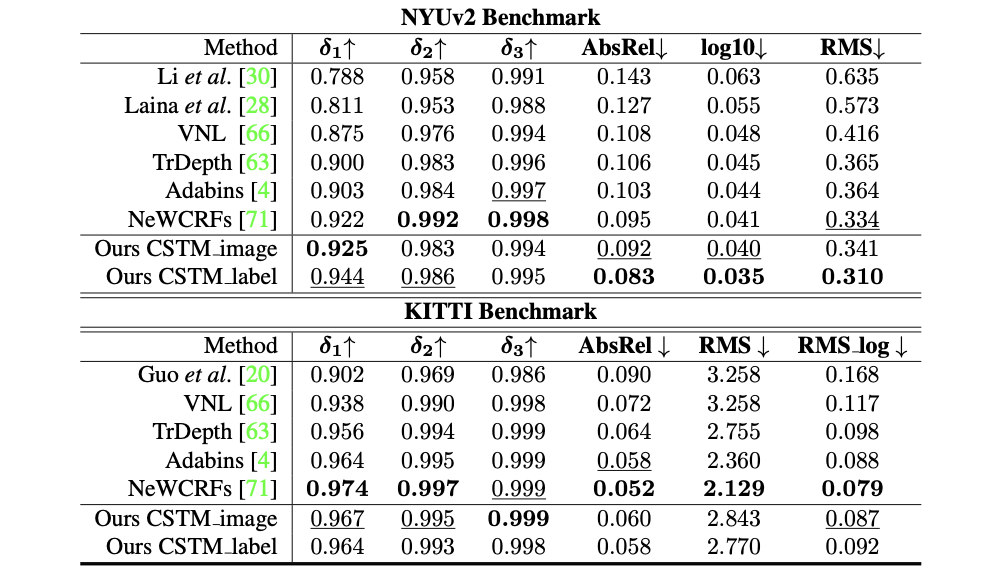
Metric3D:Towards Zero-shot Metric 3D Prediction from A Single Image
参考代码:Metric3D 介绍 在如MiDas、LeReS这些文章中对于来源不同的深度数据集使用归一化深度作为学习目标,则在网络学习的过程中就天然失去了对真实深度和物体尺寸的度量能力。而这篇文章比较明确地指出了影响深度估计尺度变化大的因素就是焦距 f f f…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
