算法练习--leetcode 数组
文章目录
- 爬楼梯问题
- 裴波那契数列
- 两数之和 [数组]
- 合并两个有序数组
- 移动零
- 找到所有数组中消失的数字
- 三数之和
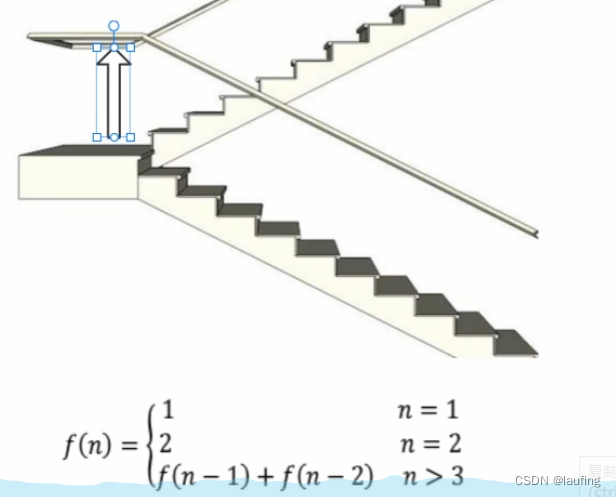
爬楼梯问题
输入n阶楼梯,每次爬1或者2个台阶,有多少种方法可以爬到楼顶?
示例1:输入2, 输出2
一次爬2阶;
一次爬1阶;
故两种方法。
示例2:
输入3, 输出3
三个1;
一个1 + 一个 2;
一个2 + 一个1;
思路分析:
采用递归求解
python实现:
# 递归
def climb_stairs(n):if n == 1:return 1elif n == 2:return 2elif n >= 3:return climb_stairs(n-1) + climb_stairs(n-2)# 递归优化,避免重复计算(优化效果微小)
def climb_stairs_2(n):d = {}if n == 1:return 1elif n == 2:return 2elif n >= 3:if n in d:return d.get(n) # 避免一部分递归操作cur = climb_stairs(n-1) + climb_stairs(n-2)d[n] = curreturn cur# 循环一次计算(自底向上依次计算)
# O(n)
def climb_stairs_3(n):if n == 1:return 1elif n == 2:return 2elif n >= 3:a = 1b = 2result = 0for i in range(3, n+1):result = a + ba = bb = resultreturn result
java实现:
// O(n)
class Solution{public int climbStairs(int n){if(n == 1) return 1;else if(n == 2) return 2;else if(n >= 3){int result = 0;int a = 1;int b = 2;for(int i=3; i<=n; i++){result = a + b;a = b;b = result;}return result;}}
}
裴波那契数列

类似爬楼梯问题。
两数之和 [数组]
给定一个整数数组 nums 和一个整数目标值 target,在该数组中找出 和 等于目标值 target 的那两个整数,并返回它们的数组下标。
假设每种输入只会对应一个答案,且数组中同一个【位置】的元素在答案里不能重复出现。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
暴力解法:
- 依次遍历元素,计算求和,并比较。
- 时间复杂度 O ( n 2 ) {O(n^2)} O(n2)
- python实现
# O(n^2)
def calcSum(arr, target):n = len(arr)for i in range(n-1):for j in range(i+1, n):if arr[i] + arr[j] == target:return [i, j]raise ValueError("未找到结果")
- java实现
在这里插入代码片
哈希优化
- 遍历数组,索引为 i;
- 判断 left = target - array[i] ,left 值是否存在于hash;
- 存在,则返回索引 i 和 hash中left 对应的值;
- 不存在,则将 array[i] :i 存入hash;
- 时间复杂度 O ( n ) {O(n)} O(n)
- python实现
# python
def optimize_calc_sum(alist, target):dict_ = {}n = len(alist)for i in range(n):if target - alist[i] in dict_:return [i, dict_.get(target - alist[i])]dict_[alist[i]] = iraise ValueError("未找到结果")
- java实现
在这里插入代码片
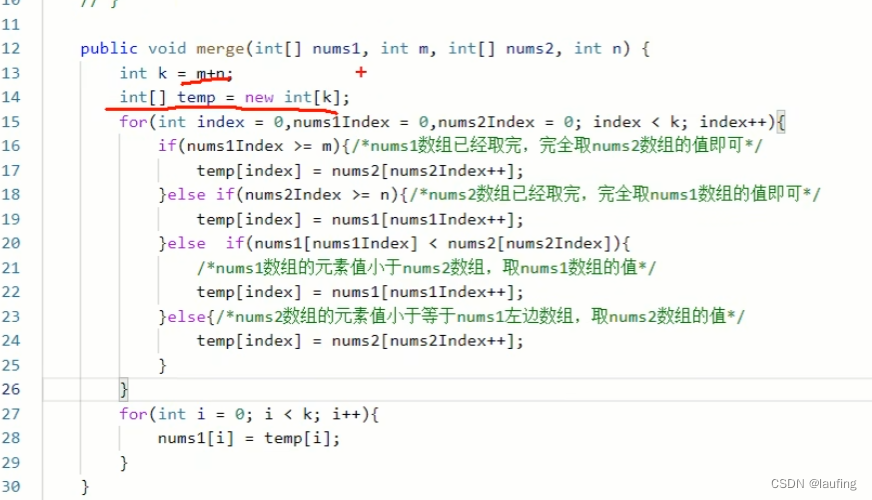
合并两个有序数组
给两个非递减排列的整数数组arr1、arr2,m 和 n 分别表示arr1 、arr2的元素个数;合并arr2到arr1中,合并后元素非递减排列。
示例1:
arr1 = [1, 2, 3, 0, 0, 0] m = 3
arr2 = [2, 5, 6] n = 3
合并结果:[1,2,2,3,5,6] 黑体数字为arr2中的元素
示例2:
arr1 = [1]
arr2 = [ ]
合并结果: [1]
python实现:
arr1 = [1, 3, 4, 0, 0, 0]
m = 3
arr2 = [2, 5, 6]
n = 3def merge_array(arr1, m, arr2, n):# 准备临时数组temp = [] # 空间复杂度O(m+n)i = 0j = 0while i < m and j < n: # O(m+n) 线性复杂度if arr1[i] <= arr2[j]:temp.append(arr1[i])i += 1else:temp.append(arr2[j])j += 1if i == m:temp.extend(arr2[j:n])elif j == n:temp.extend(arr1[i:m])for i in range(m + n):arr1[i] = temp[i]print("arr1:", arr1)return arr1java实现:
移动零
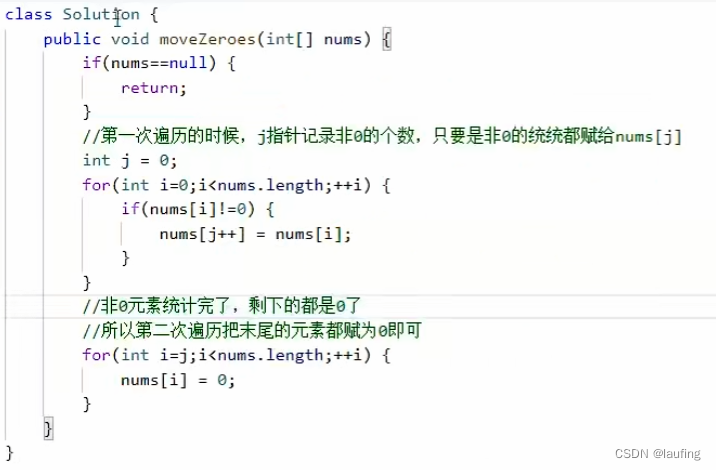
给定一个数组array,将内部所有的0移动到数组的末尾,并保持非零元素的相对顺序。必须原位操作,不能拷贝额外的数组。
示例:
输入,[0, 1, 0, 3, 12]
输出,[1, 3, 12, 0, 0]
提示:双指针
python实现:
# 暴力实现
arr = [0, 1, 0, 3, 12, 0, 0, 13, 0, 14, 0, 18, 0, 0, 0]# 依次将遍历的首个0值与后面的非0置换
def move_zero(arr):n = len(arr)for i in range(n):if arr[i] != 0:continuek = i # 记录当前0的位置j = i + 1 # 下一个元素的位置while j < n:if arr[j] == 0:j += 1continuearr[k], arr[j] = arr[j], arr[k]k = jj += 1print("result:", arr)return arr# 双指针
# 双指针同时从0开始
# 依次将后一个指针的非0值,放到前一个指针的位置,前一个指针+1,继续下次循环
# 最后将后一个指针处到结束 均赋值0
# 时间复杂度 O(2n)
def move_zero_double_pointer(arr):n = len(arr)j = 0 # j指针for i in range(n): # i指针 两个指针同时从0开始if arr[i] != 0:arr[j] = arr[i]j += 1# 将从j开始的元素 全部赋值0while j < n: # 时间复杂度 O(2n)arr[j] = 0j += 1print("result:", arr)return arr
java实现:双指针移动0
找到所有数组中消失的数字
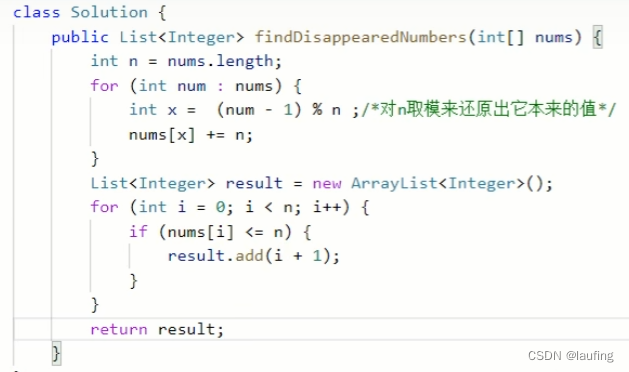
给定一个n个整数的数组array,每个元素值在【1,n】之间,找出1-n内没有出现在array中的数字,以数组形式返回。
n为数组的长度;
示例1:
输入:[4,3,2,7,8,2,3,1]
输出:[5,6]
示例2:
输入:[1,1]
输出:[2]
进阶:可以不借助额外空间且时间复杂度为O(n),解决吗?
python实现:
# 暴力实现
def find_missing_digit(arr):n = len(arr) # [1, ..., n]# arr去重temp = [] # 空间复杂度O(n)for i in range(1, n+1): # 时间复杂度 O(n)if i not in arr:temp.append(i)print("result:", temp)return temp# 优化空间复杂度O(1)
# 只能依赖数组本身的空间
# 所有元素的值 - 1 可以对应索引,对应索引处的值 都+n 或者2n....
# 而缺失的那些值 - 1 对应的索引处的值肯定没有变化,即 <= n
# 最后循环找到<=n的元素,其索引+1 就是缺失的值
def optimize_find_missing_digit(arr):n = len(arr)# 空间复杂度为O(1) 只能使用数组本身的空间for i in arr:idx = (i - 1) % n # 得到对应的索引(拿到的i可能是已改过的) 所以需要还原索引arr[idx] += 2 * ntemp = [] # 存储最终结果的空间不算 额外空间for i in range(n):if arr[i] <= n:temp.append(i + 1)print("result:", temp)return tempjava实现:
三数之和
给一个整数数组 nums ,判断是否存在三元组 [ nums[i], nums[j], nums[k] ] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。返回所有和为 0 且不重复的三元组,如果三个元素只是顺序不同,则算重复的三元组。
示例 1:
输入:[-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:[0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:[0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000
-105 <= nums[i] <= 105
python实现:
# 暴力解法 O(n^3) 会产生重复的三元组
arr = [-1,0,1,2,-1,-4]
def three_nums_sum(arr: List[int]) -> List[List[int]]:n = len(arr)temp = []for i in range(n-2):for j in range(i+1, n-1):for k in range(j+1, n):if arr[i] + arr[j] + arr[k] == 0:temp.append([arr[i], arr[j], arr[k]])# result: [[-1, 0, 1], [-1, 2, -1], [0, 1, -1]]# 会产生重复的三元组print("result:", temp)return temp# 排序 + 双指针
# 时间复杂度 O(n^2)
def optimize_three_nums_sum(nums: List[int]) -> List[List[int]]:n = len(nums)res = []if n < 3:return []nums.sort() # 排序 快排 O(nlogn)res = []for i in range(n): O(n^2)if (nums[i] > 0):return resif (i > 0 and nums[i] == nums[i - 1]): # 防止重复解continue# 双指针L = i + 1R = n - 1while (L < R):if (nums[i] + nums[L] + nums[R] == 0):res.append([nums[i], nums[L], nums[R]])# 去除重复while (L < R and nums[L] == nums[L + 1]):L = L + 1while (L < R and nums[R] == nums[R - 1]):R = R - 1L = L + 1R = R - 1elif (nums[i] + nums[L] + nums[R] > 0):R = R - 1else:L = L + 1return res
java实现:
pass
[下一篇]:算法练习–leetcode 链表
相关文章:

算法练习--leetcode 数组
文章目录 爬楼梯问题裴波那契数列两数之和 [数组]合并两个有序数组移动零找到所有数组中消失的数字三数之和 爬楼梯问题 输入n阶楼梯,每次爬1或者2个台阶,有多少种方法可以爬到楼顶? 示例1:输入2, 输出2 一次爬2阶&a…...

本地 shell无法连接centos 7 ?
1、首先检查是否安装ssh服务; yum list installed | grep openssh-server# 没有安装尝试安装下 yum install openssh-server 2、检查ssh服务是否开启 systemctl status sshd.service# 未开启,开启下 systemctl start sshd.service # 将sshd 服务添…...

C 语言的基本算术运算符 = + - * /
C 语言的基本算术运算符有: - * / 赋值运算符 赋值运算符左侧必须引用一个内存中的位置, 最简单的方法就是使用变量名, 也可以使用指针指向内存中的某个位置. 赋值表达式的目的是把值储存到目标内存位置上. 下面语句中的 表示初始化而不是赋值: const int …...

SQL注入实操三(SQLilabs Less41-50)
文章目录 一、sqli-labs靶场1.轮子模式总结2.Less-41 stacked Query Intiger type blinda.注入点判断b.轮子测试c.获取数据库名称d.堆叠注入e.堆叠注入外带注入获取表名f.堆叠注入外带注入获取列名g.堆叠注入外带注入获取表内数据 3.Less-42 Stacked Query error baseda.注入点…...

HOT77-买卖股票的最佳时机
leetcode原题链接:买卖股票的最佳时机 题目描述 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所…...
CSS调色网有哪些
本文章转载于湖南五车教育,仅用于学习和讨论,如有侵权请联系 1、https://webgradients.com/ Wbgradients 是一个在线调整渐变色的网站 ,可以根据你想要的调整效果,同时支持复制 CSS 代码,可以更好的与开发对接。 Wbg…...

Day10-NodeJS和NPM配置
Day10-NodeJS和NPM 一 Nodejs 1 简介 Nodejs学习中文网:https://www.nodeapp.cn/synopsis.html Nodejs的官网:https://nodejs.org/ 概念:Nodejs是JavaScript的服务端运行环境.Nodejs不是框架,也不是编程语言,就是一个运行环境. Nodejs是基于chrome V8引擎开发的一套js代码…...
线性代数 | 机器学习数学基础
前言 线性代数(linear algebra)是关于向量空间和线性映射的一个数学分支。它包括对线、面和子空间的研究,同时也涉及到所有的向量空间的一般性质。 本文主要介绍机器学习中所用到的线性代数核心基础概念,供读者学习阶段查漏补缺…...
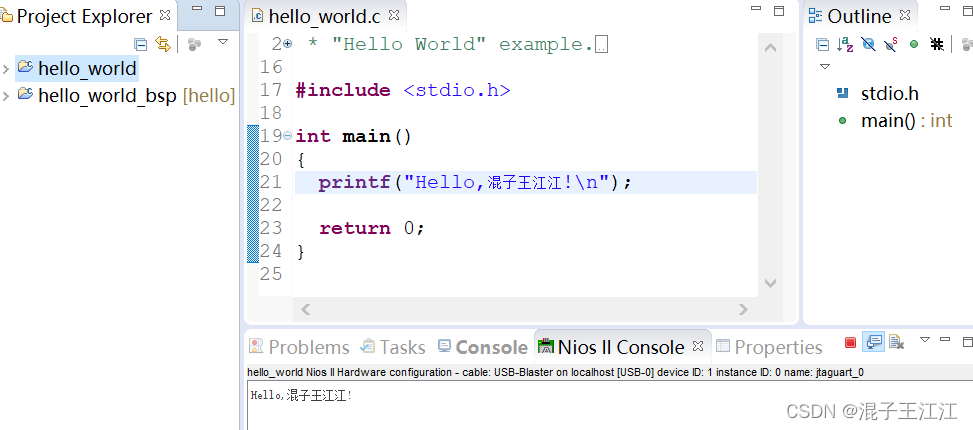
Nios初体验之——Hello world!
文章目录 前言一、系统设计1、系统模块框图2、系统涉及到的模块1、时钟2、nios2_qsys3、片内存储(onchip_rom、onchip_ram)4、串行通信(jtag_uart)5、System ID(sysid_qsys) 二、硬件设计1、创建Qsys2、重命…...

[Linux]理解文件系统!动静态库详细制作使用!(缓冲区、inode、软硬链接、动静态库)
hello,大家好,这里是bang___bang_,今天来谈谈的文件系统知识,包含有缓冲区、inode、软硬链接、动静态库。本篇旨在分享记录知识,如有需要,希望能有所帮助。 目录 1️⃣缓冲区 🍙缓冲区的意义 …...
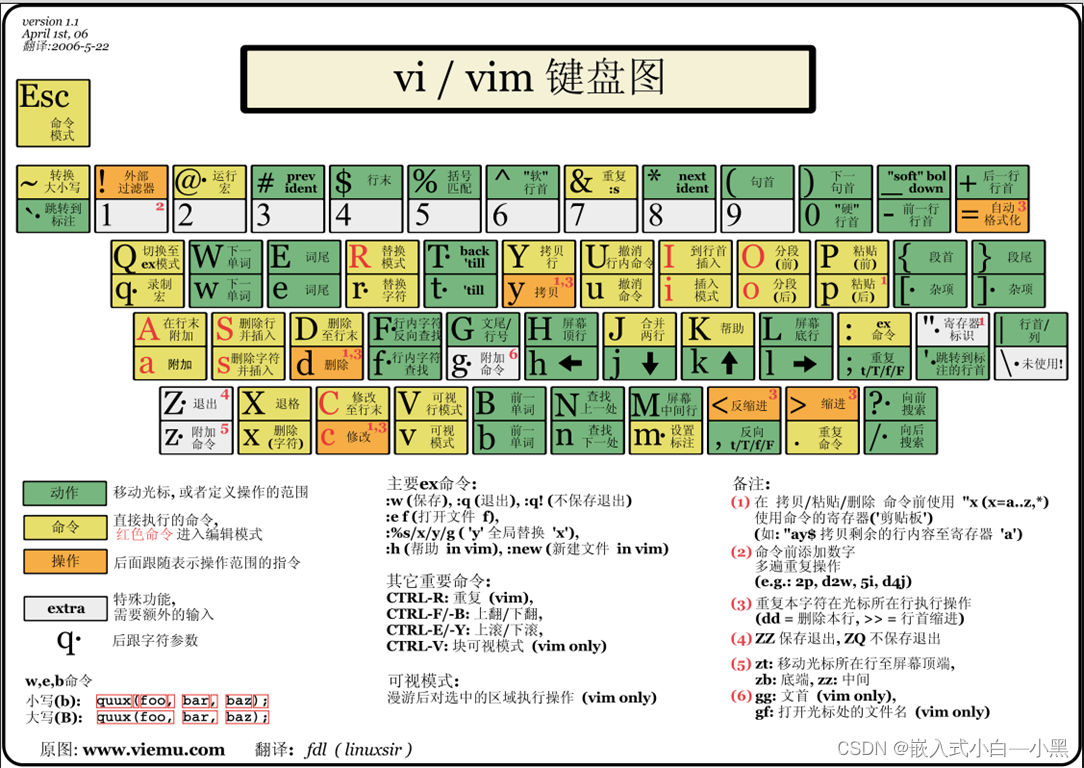
【Linux操作系统】Vim:提升你的编辑效率
Vim是一款功能强大的文本编辑器,它具有高度可定制性和灵活性,可以帮助程序员和文本编辑者提高编辑效率。本文将介绍Vim的基本使用方法、常用功能和一些实用技巧。 文章目录 1. Vim的基本使用方法:2. 常用功能:2.1 文件操作&#…...
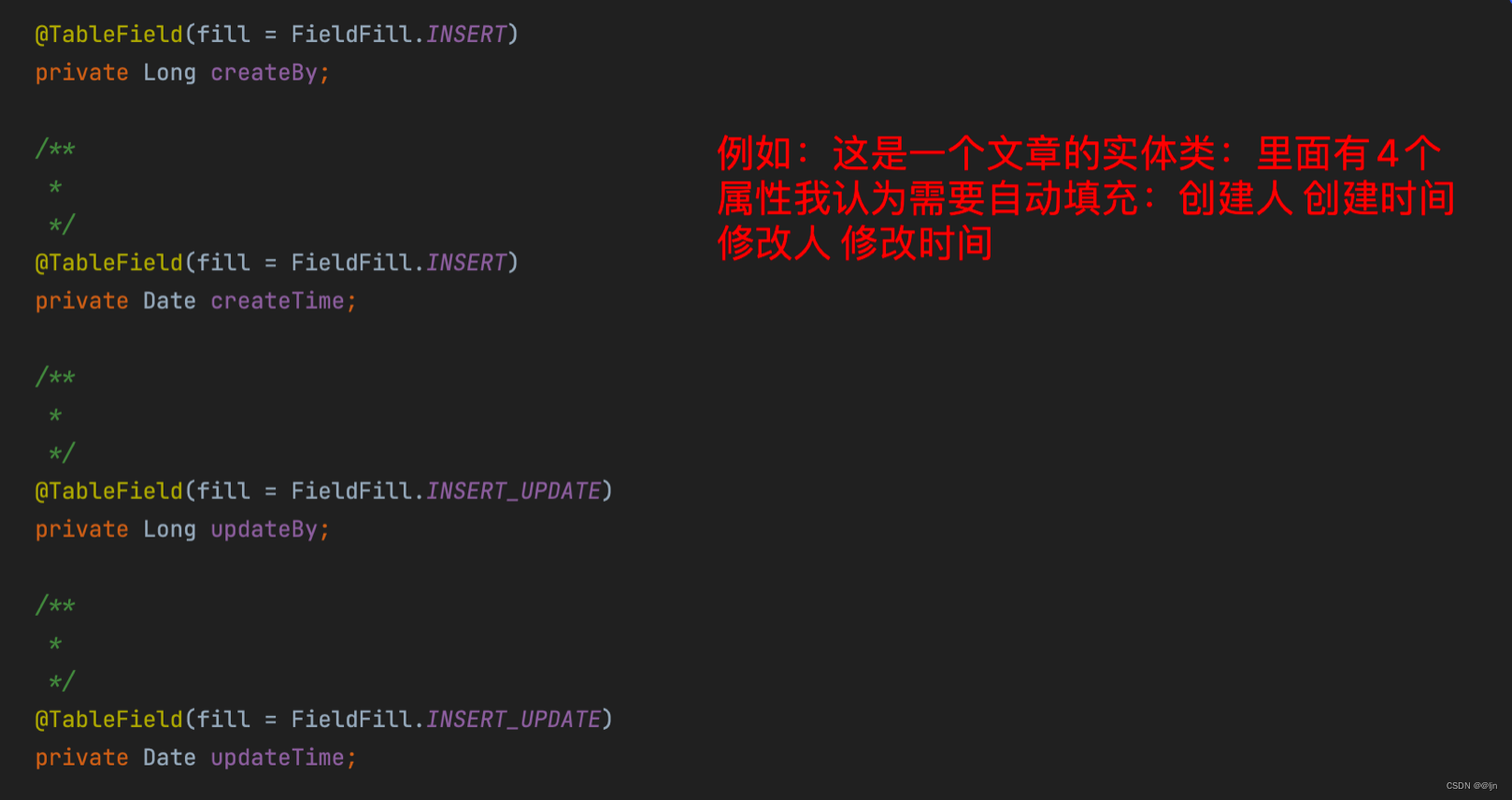
Mybatis-plus 的自动填充策略
当在项目中需要对某些实体类中的公共的属性进行自动填充时,可以使用Mybatis-plus中的自动填充功能。 (1)我们可以在实体类中把要自动填充的类属性加上指定的注解TableField(填写在上面方法时进行填充的枚举类型填充策略ÿ…...
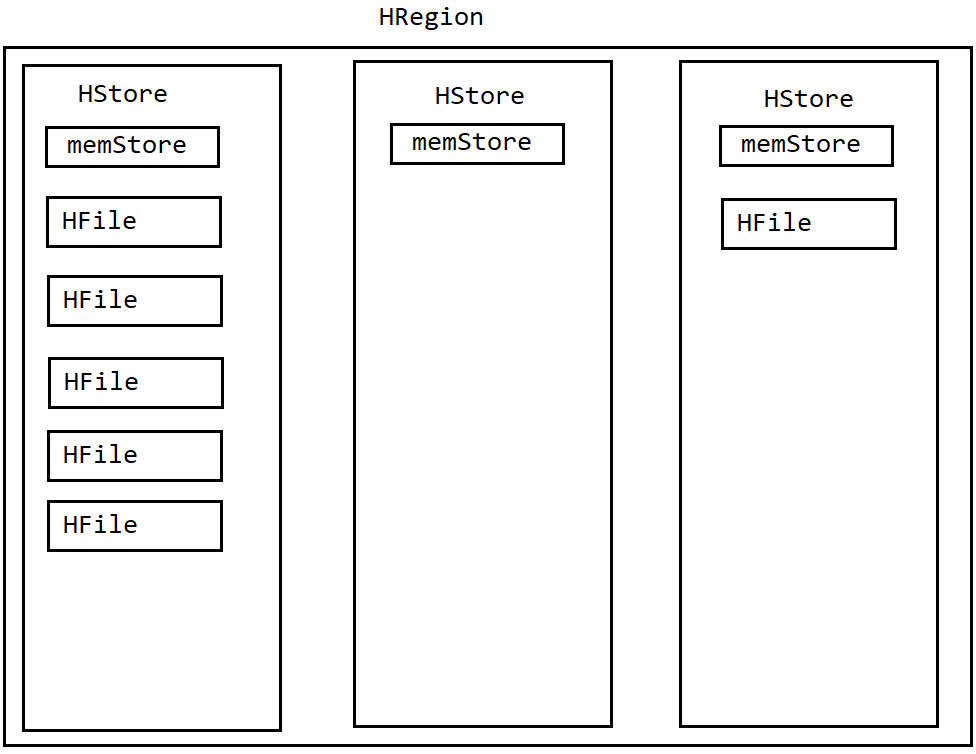
大数据课程G2——Hbase的基本架构
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 掌握Hbase的基本架构; ⚪ 掌握Hbase的读写流程; ⚪ 掌握Hbase的设计与优化; 一、基本架构 1. HRegion 1. 在HBase中,会将一个表从行键方向上进行切分,切分成1个或者多个HRegion。 …...
微信小程序wx.getlocation接口权限申请总结
先附上申请通过截图 插播内容:可代开通,保证通过。wx.getLocation接口(获取当前的地址位置) qq: 308205428 如何申请 当申请微信小程序的wx.getLocation接口权限时,你可以…...

简单游戏截图_可控截取内容1
一个需求 我需要在场景中截取不同层级的截图(如只截模型或只截UI或只截外部相加看到的画面 或全都截或和Shader配合呈现人眼夜视仪热成像的画面切换) 将截图排到列表中,在场景UI中展示出来 如何做 相机要能够看到不同的画面 将当前帧画面存储下来 将存储的画面展示出…...
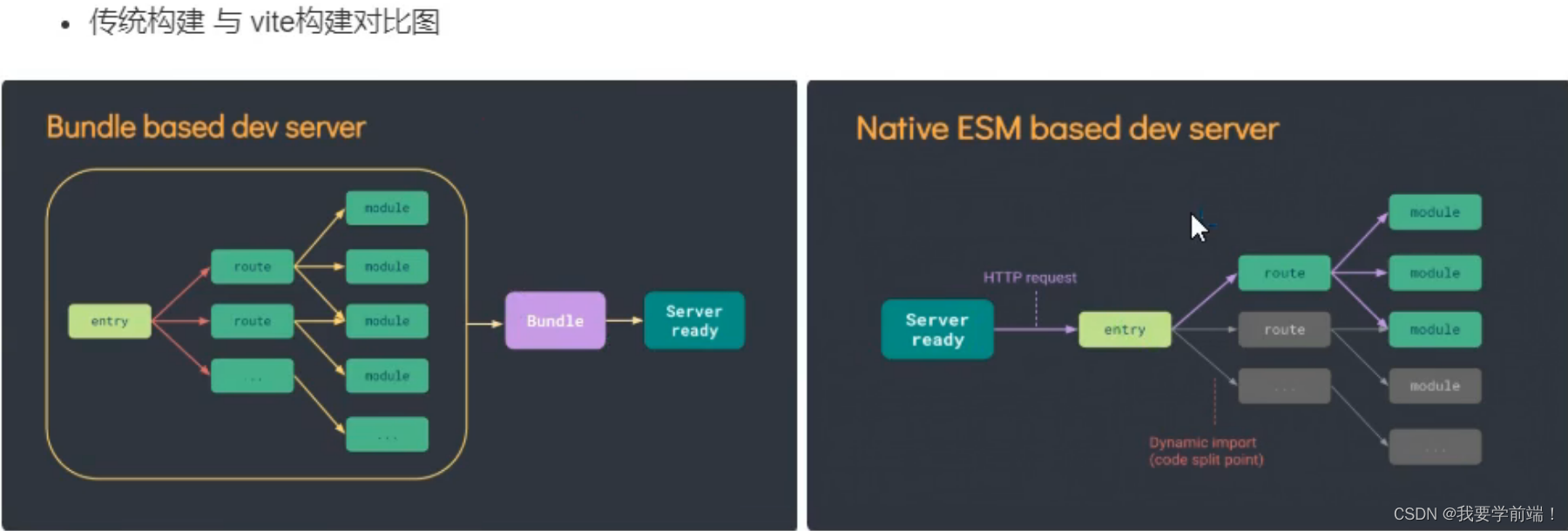
Vue3_02 创建Vue3.0工程
1.使用 vue-cli 创建 ## 查看 vue/cli 版本,确保 vue/cli 版本在4.5.0以上 vue -V 或 vue --version## 安装或升级你的 vue/cli npm install -g vue/cli## 创建 vue create vue_test## 启动 cd vue-test npm run serve 2.使用 vite 创建 什么是vite?——新一代…...

Arduino ESP 8266 ESPAsyncWebServer AsyncCallbackJsonWebHandler
Arduino-ESP 8266 踩坑(一) ESPAsyncWebServer AsyncCallbackJsonWebHandler 在使用 ESPAsyncWebServer 时 由于我想用 asyncWebServer 通过 application/json POST 请求拿数据, 就翻看了 ESPAsyncWebServer 的 git 文档, 他是这样说的 : //JSON body handling with ArduinoJ…...
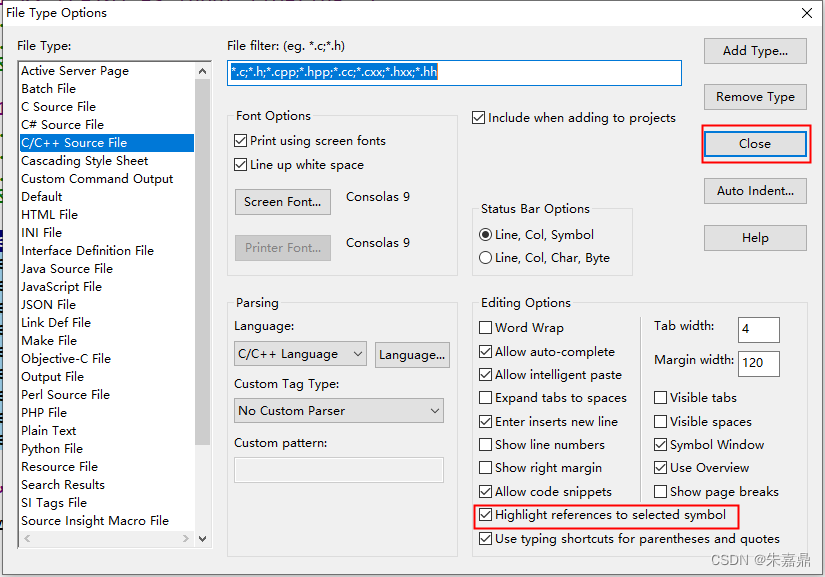
Source Insight_突出显示对选定字符的引用
1、突出显示对选定字符的引用 在Source Insight中,当我们选中一个函数或者变量的时候,关于它的所有引用地方都高亮显示,想要实现效果如下。 2、配置方法 (1)点击"Options"→“File Type options...” (2)勾选“Highlight referenc…...

高等数学上册 第五章 定积分 知识点总结
定积分 定积分的性质: ( 1 ) ∫ a b [ α f ( x ) β g ( x ) ] d x α ∫ a b f ( x ) d x β ∫ a b g ( x ) d x ( 2 )设 a < c < b ,则 ∫ a b f ( x ) d x ∫ a c f ( x ) d x ∫ c b f ( …...

【无标题】uniapp引入萤石云 真机无法运行 踩坑集合
Uniapp 接入萤石云 踩坑 1.先用了 UIKit Javascript 就是在 pc端 那套流程 npm install ezuikit-jsimport EZUIKit from ezuikit-js;这套流程貌似只适用于pc端,我在接入uniapp的时候没看官网 以为都是一套流程,然后就在uniapp中也来了这一套࿰…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
