【树形DP+换根思想】2022牛客多校加赛 H
登录—专业IT笔试面试备考平台_牛客网
题意:


思路:
这个虽然是树形DP,却用了换根的思想....
首先,后缀0的个数可以转化成min(cnt2,cnt5),其中cnt2为2的因子个数,cnt5为5的因子个数
然后进行DP
设dp[u][0/1]为,在除了u这棵子树中,2/5的因子个数
为什么要这么设计,我们发现,如果计算的结点是在子树里面的,那么lca就是u,子树的贡献直接就是sz[u]*cnt[u][0/1]
但是在这棵子树之外的贡献不能这么求,因此需要额外设计
然后转移就很简单:
dp[v][j]=dp[u][j]+(sz[u]-sz[v])*cnt[u][j]
最后统计贡献的时候加上子树部分的贡献,取min(cnt2,cnt5)就好了
Code:
#include <bits/stdc++.h>#define int long longusing namespace std;const int mxn=2e5+10;
const int mxe=1e6+10;
const int mxv=1e6+10;
const int mod=998244353;
const int Inf=1e18;vector<int> G[mxn];int N,Q;
int u,v,x;
int sz[mxn];
int dp[mxn][2],cnt[mxn][2];void init(){for(int i=1;i<=N;i++){if(i%2==0){int t=i,s=0;while(t%2==0) t/=2,s++;cnt[i][0]=s;}if(i%5==0){int t=i,s=0;while(t%5==0) t/=5,s++;cnt[i][1]=s;}}
}
void dfs1(int u,int fa){sz[u]=1;for(auto v:G[u]){if(v==fa) continue;dfs1(v,u);sz[u]+=sz[v];}
}
void dfs2(int u,int fa){for(auto v:G[u]){if(v==fa) continue;for(int j=0;j<=1;j++){dp[v][j]=dp[u][j]+(sz[u]-sz[v])*cnt[u][j];}dfs2(v,u);}
}
void solve(){cin>>N>>Q;init();for(int i=1;i<=N-1;i++){cin>>u>>v;G[u].push_back(v);G[v].push_back(u);}dfs1(1,0);dfs2(1,0);while(Q--){cin>>x;int res=1e18;for(int j=0;j<=1;j++){res=min(res,dp[x][j]+sz[x]*cnt[x][j]);}cout<<res<<'\n';}
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;while(__--)solve();return 0;
}相关文章:

【树形DP+换根思想】2022牛客多校加赛 H
登录—专业IT笔试面试备考平台_牛客网 题意: 思路: 这个虽然是树形DP,却用了换根的思想.... 首先,后缀0的个数可以转化成min(cnt2,cnt5),其中cnt2为2的因子个数,cnt5为5的因子个数 然后进行DP 设dp[u]…...

Gitlab CI/CD笔记-第二天-GitOps的流水线常用关键词(1)
一、常用关键词 在Gitlab项目的根目录需要创建一个 .gitlab-ci.yaml的文件。 这个文件就是定义的流水线。Call :"Pipeline as code" 二、这条流水线怎么写? 一、掌握常用的关键词即可。 1.关键词分类 1.全局关键词 Global Keywards 2.任务关键词…...
Spring Boot3.0(一):入门篇
什么是 Spring Boot Spring Boot 是由 Pivotal 团队提供的全新框架,其设计目的是用来简化新 Spring 应用的初始搭建以及开发过程。该框架使用了特定的方式来进行配置,从而使开发人员不再需要定义样板化的配置。 用我的话来理解,就是 Spring…...

各种排序333
冒泡排序 n方 public static void BubbleSort(int[] arr) {int n = arr.Length;for (int i = 0; i < n - 1; i++){for (int j = 0; j < n - i - 1; j++){if (arr[j] > arr[j + 1]){int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}} }选择排序 n方 publ…...
[C++] 类与对象(中)完整讲述运算符重载示例 -- 日期类(Date) -- const成员
目录 1、前言 2、全缺省的构造函数 3、打印接口 4、拷贝构造 5、赋值运算符重载(operator) 5.1赋值重载是默认成员函数,重载格式: 5.2 赋值重载不能为全局函数 5.3 编译器默认生成 6、析构函数 7、operator> 8、ope…...

wonderful-sql 作业
Sql 作业 作业1: 答: create table Employee (Id integer not null, Name varchar(32) , Salary integer, departmentId integer, primary key (Id) );create table Department( Id integer primary key, Name varchar(30) not null );insert into emp…...
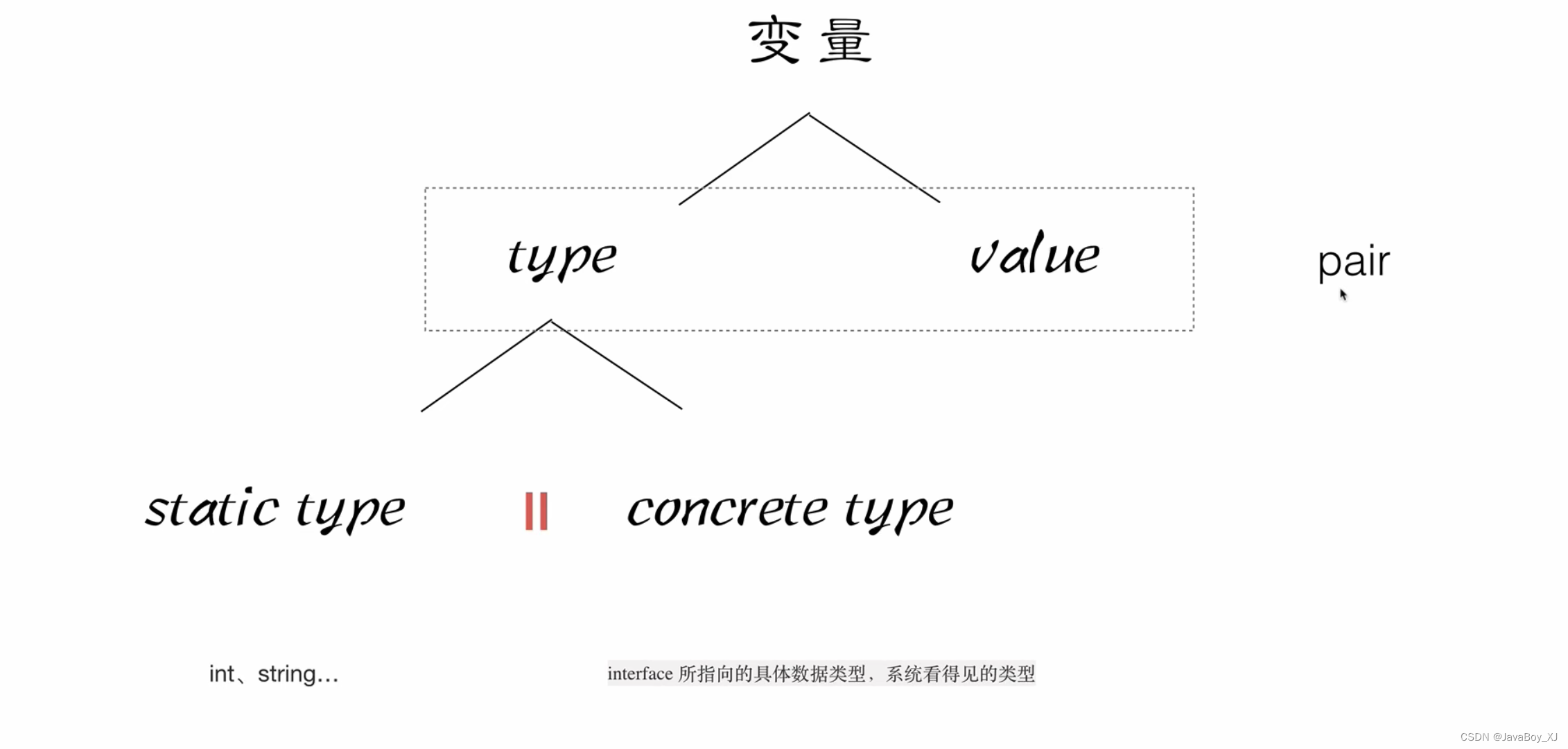
Go学习第六天
Golang变量内置pair结构详细说明 变量包括(type, value)两部分type 包括 static type和concrete type. 简单来说 static type是你在编码是看见的类型(如int、string),concrete type是runtime系统看见的类型类型断言能否成功,取决…...

opencv-34 图像平滑处理-2D 卷积 cv2.filter2D()
2D卷积是一种图像处理和计算机视觉中常用的操作,用于在图像上应用滤波器或卷积核,从而对图像进行特征提取、平滑处理或边缘检测等操作。 在2D卷积中,图像和卷积核都是二维的矩阵或数组。卷积操作将卷积核在图像上滑动,对每个局部区…...

Java 克隆技术详解,深拷贝与浅拷贝的区别及实现
什么是克隆,为什么在编程中使用克隆 克隆是指创建一个对象的副本,使得新创建的对象在内容上与原始对象相同。在编程中,克隆是常用的技术之一,它具有以下几个重要用途和优势: 复制对象:使用克隆可以创建一个…...

包装器function
std::function模板类是一个通用的可调用对象的包装器,用简单的、统一的方式处理可调用对象。 template<class _Fty> class function…… _Fty是可调用对象的类型,格式:返回类型(参数列表)。 包含头文件:#include <functi…...
Django Rest_Framework(三)
文章目录 1. 认证Authentication2. 权限Permissions使用提供的权限举例自定义权限 3. 限流Throttling基本使用可选限流类 4. 过滤Filtering5. 排序Ordering6. 分页Pagination可选分页器 7. 异常处理 ExceptionsREST framework定义的异常 8. 自动生成接口文档coreapi安装依赖设置…...

总结 IO、存储、硬盘、文件系统相关常识
目录 一、IO是什么? 二、存储 三、硬盘 四、文件系统 4.1 文件目录和组织方式 4.2 文化路径 4.3 文件类型 4.4 文件系统操作 一、IO是什么? IO是英文Input/Output的缩写,指输入/输出。在计算机科学中,IO通常指计算机与外部设备或…...

JavaScript、深入浅出Node.js前端技能汇总
JavaScript 前端技能汇总 Frontend Knowledge Structure 深入浅出Node.js 书籍pdf 《深入浅出Node.js》的相关代码 Javascript&jQuery教程 pdf html & css教程 pdf 高性能JavaScript_中英双语版 pdf 跳坑之js调用另一个js文件中函数 方法1; 在html文件中加入两…...

use gnustep objective-c
first app #import <Foundation/Foundation.h>int main(int argc, const char * argv[]) {NSAutoreleasePool *pool [NSAutoreleasePool new];NSLog("first start");[pool drain];return 0; }tech 专注于概念,而不是迷失在语言技术细节中编程语言…...

8.15锁的优化
1.锁升级(锁膨胀) 无锁 -> 偏向锁 -> 轻量级锁 -> 重量级锁 偏向锁:不是真的加锁,而是做了一个标记,如果有别的线程来竞争才会真的加锁,如果没有别的线程竞争就不会加锁. 轻量级锁:一个线程占领锁资源后,另一个线程通过自旋的方式反复确认锁是否被是否(这个过程比较…...
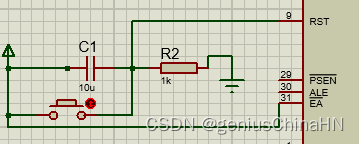
单片机复位电路分析
来分析一下这个电路: 首先这里面有电容,所以是一个动态电路。哈哈哈 假设左上角的电压源是5V的代号为VOLT。 可以知道电容capacitor C1左边的电压也是5V,电容中间隔着一个绝缘体,所以不导电, 这个时候电流无法通过…...

公文写作技巧:“三面镜子”写作提纲60例
写作技巧:“三面镜子”写作提纲60例 1. 用好“三面镜子” 推深做实警示教育 勤用“反光镜”以案为鉴。 善用“显微镜”以案明纪。 巧用“聚光镜”以案促改。 2. 年轻干部要用好“三面镜子” 用好“反光镜”,照亮基层中的“暗点” 用好“显微镜”&am…...

useEffect中的函数会执行2次原因
一、useEffect介绍 useEffect是React18的新特性,表示React的生命周期Hooks组件。等价于Claas组件的componentDidMount、componentDidUpdate,useEffect的返回函数等价于componentWillUnmount。(组件卸载、重新挂载都会触发这个函数,…...
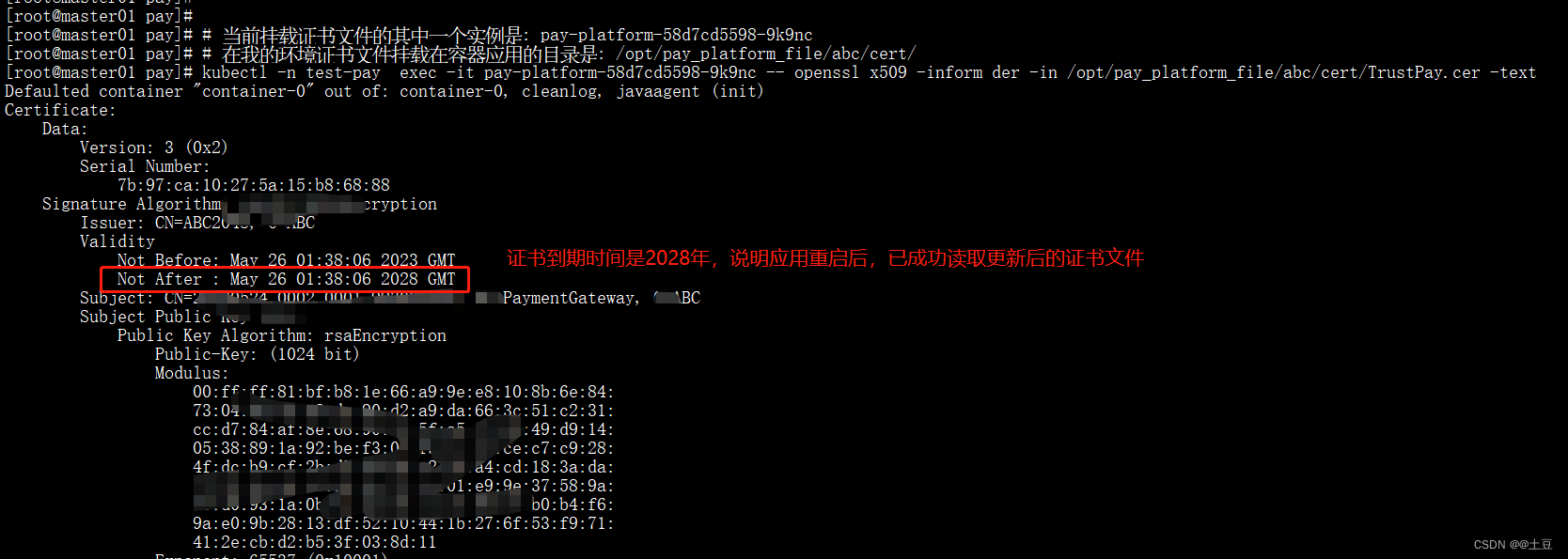
更新k8s环境支付系统支付证书
目录 一、背景 二、更新支付系统银行证书 三、备份旧的secret信息 四、更新支付应用的证书信息 五、重启支付系统的应用 六、验证应用实例挂载的秘钥已更新 一、背景 支付系统是基于k8s容器化部署的微服务,支付系统使用的支付证书以及和银行有关的证书都是保存…...

C#的yield
在 C# 中,yield 关键字用于定义迭代器方法(Iterator Methods),并使其返回一个可枚举的序列。通过使用 yield 关键字,可以简化迭代器的实现,使其更加直观和易于理解。 使用 yield 关键字定义的方法被称为迭…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
