2308C++搞笑的概念化
前一篇的概念化,太搞笑
元<类 T>概念 可画=要求(T&t,整 i){t.画(i);};
构 方形{空 画(整 i){打印(2*i);}
};元<可画 T>空 f(T&t,整 i){t.画(i);t.画(i);
}空 主(){方形 e;f(e,33);
}用得着那么复杂吗?
相关文章:

2308C++搞笑的概念化
前一篇的概念化,太搞笑 元<类 T>概念 可画要求(T&t,整 i){t.画(i);}; 构 方形{空 画(整 i){打印(2*i);} };元<可画 T>空 f(T&t,整 i){t.画(i);t.画(i); }空 主(){方形 e;f(e,33); }用得着那么复杂吗?...

修改node_modules里的源码
最近在工作中使用到一款生成二维码的依赖(以vue项目为例讲解):vue-qr,安装的4.0.9版本的,在启动工程的时候报错: You may need an appropriate loader to handle this file type后我查阅各种资料发现 1&a…...

【每日一题Day287】LC24 两两交换链表中的节点 | 模拟 递归
两两交换链表中的节点【LC24】 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 周赛暂停一周啦 思路:模拟 记录前驱…...

Java ~ Collection/Executor ~ PriorityBlockingQueue【源码】
前言 相关系列 《Java ~ Collection【目录】》(持续更新)《Java ~ Executor【目录】》(持续更新)《Java ~ Collection/Executor ~ PriorityBlockingQueue【源码】》(学习过程/多有漏误/仅作参考/不再更新)…...

Java后台生成微信小程序码并以流的形式返回给前端
后端代码 获取access_token import net.sf.json.JSONObject;public class WeChatUtil {/*** 获取token*/private static String ACCESSTOKENURL "https://api.weixin.qq.com/cgi-bin/token?grant_typeclient_credential&appid{appId}&secret{appSecret}"…...
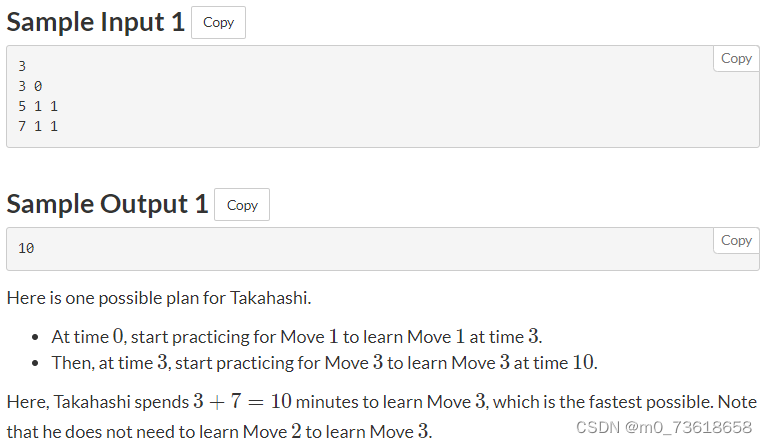
AtcoderABC226场
A - Round decimalsA - Round decimals 题目大意 给定一个实数X,它最多可以使用三位小数表示,而且X的小数点后有三位小数。将X四舍五入到最接近的整数并打印结果。 思路分析 可以使用round函数进行四舍五入 知识点 round(x) 是一个用来对数字进行四…...
Linux知识点 -- VS Code远程连接服务器协助开发
Linux知识点 – VS Code远程连接服务器协助开发 文章目录 Linux知识点 -- VS Code远程连接服务器协助开发一、VS Code的使用1.使用VS Code进行C语言编译与运行2.使用VS Code进行C代码的编译与运行 二、使用VS Code连接云服务器三、使用VS Code进行GDB调试 一、VS Code的使用 1…...
blender基础认识(选项开关、工具栏、视图等)
文章目录 引言一、大纲选项开关和保存启动文件1. 大纲选项1. 禁用选中2. 视图影藏3. 视图禁用4. 渲染禁用 2. 保存启动文件 二、工具栏和侧边栏1. 左侧工具栏2. 右侧工具栏 三、视图1. 视角2. 缩放3. 拖拽4. 摄像机视角5. 切换正交视图6. 局部视图7. 显示隐藏 四、添加删除物体…...

React Hooks 中的属性详解
React Hooks 是 React 16.8 版本中新增的特性,允许我们在不编写 class 的情况下使用 state 和其他的 React 特性。Hooks 是一种可以让你在函数组件中“钩入” React 特性的函数。以下是一些常用的 React Hooks,并附有详细的用法和代码示例。 1. useStat…...
)
工作遇到问题与解决办法(一)
一、构建父子工程 父 <groupId>com.ruoyi</groupId> <artifactId>ruoyi</artifactId> <version>3.8.5</version> <modules><module>ruoyi-admin</module><module>ruoyi-framework</module><module>…...
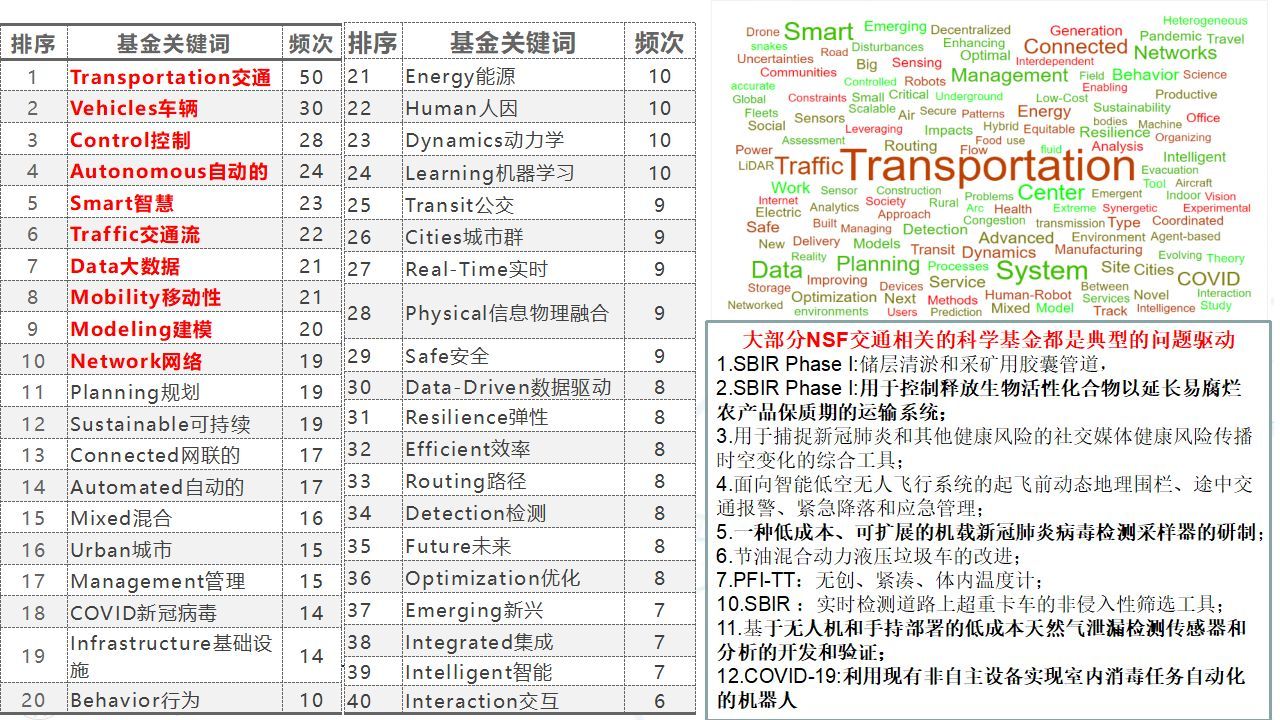
综合与新综合与新型交通发展趋势[75页PPT]
导读:原文《综合与新综合与新型交通发展趋势[75页PPT]》(获取来源见文尾),本文精选其中精华及架构部分,逻辑清晰、内容完整,为快速形成售前方案提供参考。 完整版领取方式 完整版领取方式: 如需…...

【树形DP+换根思想】2022牛客多校加赛 H
登录—专业IT笔试面试备考平台_牛客网 题意: 思路: 这个虽然是树形DP,却用了换根的思想.... 首先,后缀0的个数可以转化成min(cnt2,cnt5),其中cnt2为2的因子个数,cnt5为5的因子个数 然后进行DP 设dp[u]…...

Gitlab CI/CD笔记-第二天-GitOps的流水线常用关键词(1)
一、常用关键词 在Gitlab项目的根目录需要创建一个 .gitlab-ci.yaml的文件。 这个文件就是定义的流水线。Call :"Pipeline as code" 二、这条流水线怎么写? 一、掌握常用的关键词即可。 1.关键词分类 1.全局关键词 Global Keywards 2.任务关键词…...
Spring Boot3.0(一):入门篇
什么是 Spring Boot Spring Boot 是由 Pivotal 团队提供的全新框架,其设计目的是用来简化新 Spring 应用的初始搭建以及开发过程。该框架使用了特定的方式来进行配置,从而使开发人员不再需要定义样板化的配置。 用我的话来理解,就是 Spring…...

各种排序333
冒泡排序 n方 public static void BubbleSort(int[] arr) {int n = arr.Length;for (int i = 0; i < n - 1; i++){for (int j = 0; j < n - i - 1; j++){if (arr[j] > arr[j + 1]){int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}} }选择排序 n方 publ…...
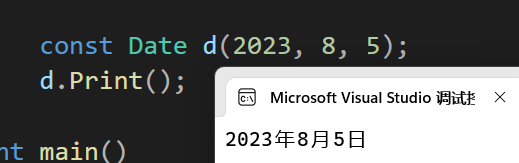
[C++] 类与对象(中)完整讲述运算符重载示例 -- 日期类(Date) -- const成员
目录 1、前言 2、全缺省的构造函数 3、打印接口 4、拷贝构造 5、赋值运算符重载(operator) 5.1赋值重载是默认成员函数,重载格式: 5.2 赋值重载不能为全局函数 5.3 编译器默认生成 6、析构函数 7、operator> 8、ope…...

wonderful-sql 作业
Sql 作业 作业1: 答: create table Employee (Id integer not null, Name varchar(32) , Salary integer, departmentId integer, primary key (Id) );create table Department( Id integer primary key, Name varchar(30) not null );insert into emp…...
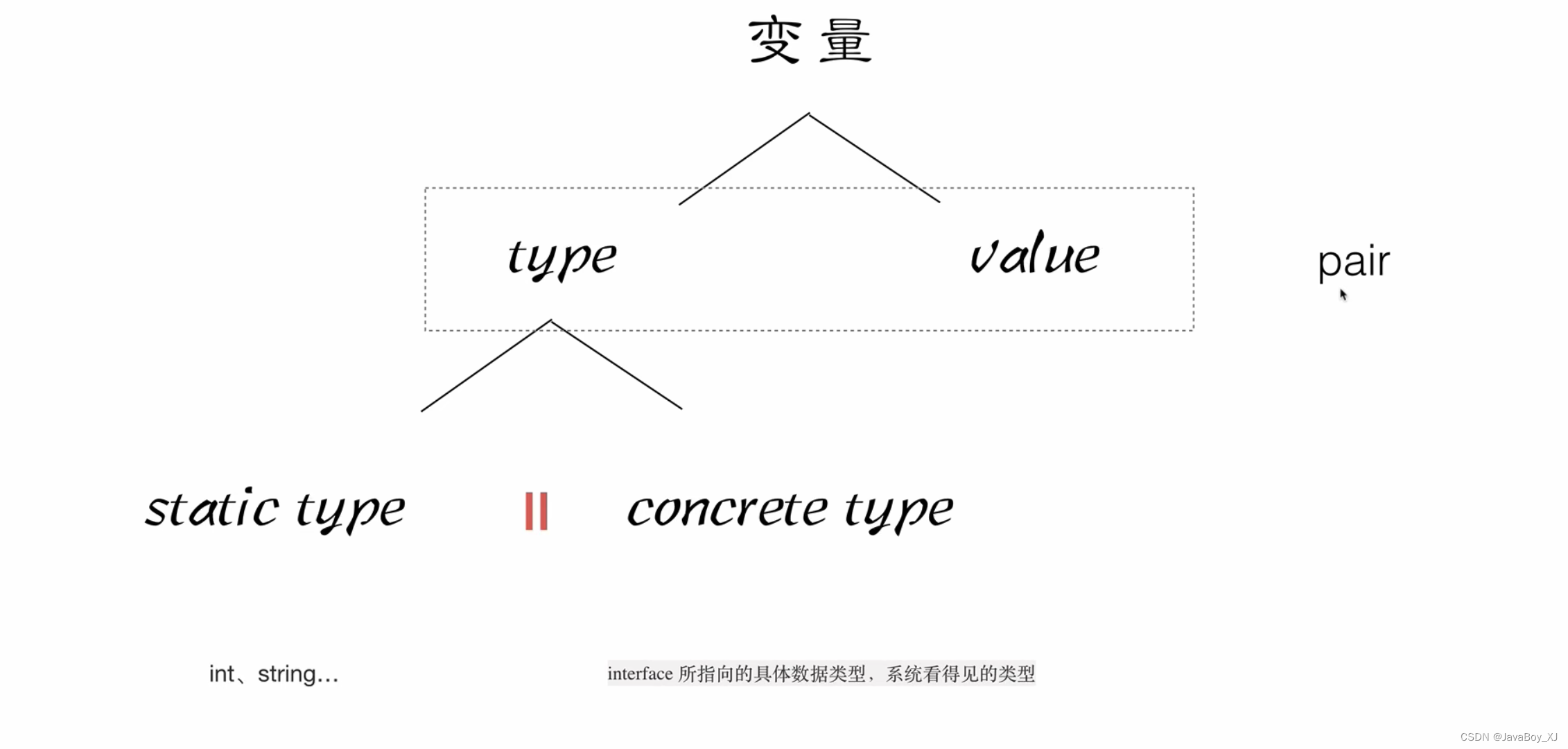
Go学习第六天
Golang变量内置pair结构详细说明 变量包括(type, value)两部分type 包括 static type和concrete type. 简单来说 static type是你在编码是看见的类型(如int、string),concrete type是runtime系统看见的类型类型断言能否成功,取决…...

opencv-34 图像平滑处理-2D 卷积 cv2.filter2D()
2D卷积是一种图像处理和计算机视觉中常用的操作,用于在图像上应用滤波器或卷积核,从而对图像进行特征提取、平滑处理或边缘检测等操作。 在2D卷积中,图像和卷积核都是二维的矩阵或数组。卷积操作将卷积核在图像上滑动,对每个局部区…...

Java 克隆技术详解,深拷贝与浅拷贝的区别及实现
什么是克隆,为什么在编程中使用克隆 克隆是指创建一个对象的副本,使得新创建的对象在内容上与原始对象相同。在编程中,克隆是常用的技术之一,它具有以下几个重要用途和优势: 复制对象:使用克隆可以创建一个…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
