【数据结构】常见的排序算法
常见的排序算法
- 常见的排序算法
- 插入排序之直接插入排序
- 时间复杂度
- 特性总结
- 插入排序之希尔排序
- 时间复杂度
- 选择排序之直接选择排序
- 特性总结
- 选择排序之堆排序
- 时间复杂度
- 特性总结
- 交换排序之冒泡排序
- 特性总结
- 交换排序之快速排序
- hoare版本
- 挖坑法
- 双指针法
- 快速排序的优化1,增加三数取中
- 快速排序的优化2,将递归算法改为非递归算法
- 快速排序的性能总结
- 归并排序
- 归并排序特性总结
常见的排序算法
常见的七大排序算法:
插入排序之直接插入排序
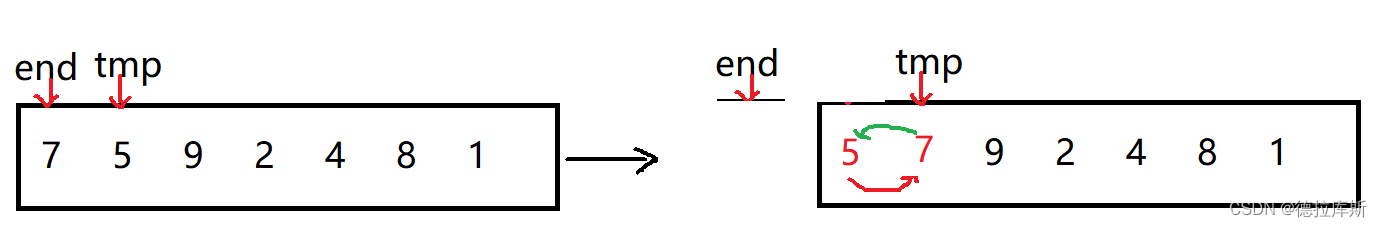
void InsertOrder(vector<int>& v)
{for (int i = 0; i < v.size() - 1; ++i){//起始end为0int end = i ;//比较的值是下标为end的下一个int tmp = v[end + 1];while (end >= 0){//如果end对应的值比tmp大,说明需要进行插入排序if (v[end] > tmp){v[end + 1] = v[end];//插入完成后end要向前走end--;}//如果end对应的值比tmp小,说明不需要进行插入,跳出当前while循环,end向后走即可elsebreak;}//一趟完成后,要将tmp赋给end的下一个位置v[end + 1] = tmp;}
}
时间复杂度
最好的情况是O(n),数组为升序
最坏的情况是O(n2),数组为降序
特性总结
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
插入排序之希尔排序
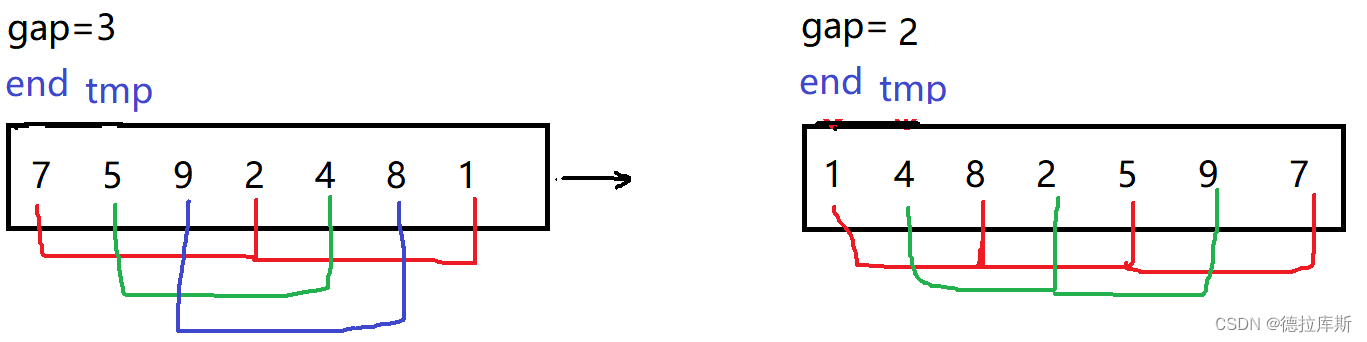
针对直接插入排序中,当数组属于降序时,时间复杂度太高,设计了希尔排序
设计思路是:当数组降序时,使用分组,可以减小排序次数,逐渐减小分组间隙,当排序次数较多时,数组本身已经快要接近有序了,以此来解决数据降序时排序复杂度高的问题。
因此希尔排序是对直接插入排序的优化
void ShellSort(vector<int>& v)
{int gap = v.size();while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < v.size() - gap; ++i){int end = i ;int tmp = v[end + gap];while (end >= 0){if (v[end] > tmp){v[end + gap] = v[end];end -= gap;}elsebreak;}v[end + gap] = tmp;}}
}
时间复杂度
O(n1.25)
选择排序之直接选择排序
设计思路是:
1.从前往后遍历整个数组,拿到当前数组最大和最小值
2.将最小值和第一个元素交换,最大值和最后一个元素交换
3.缩小数组的范围,继续上述的操作
4.直到新数组范围内只有一个元素为止
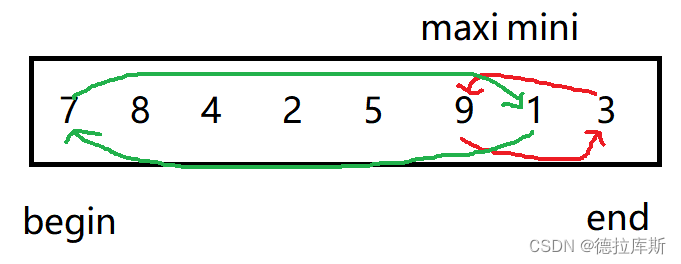
void swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}
void SelectSort(vector<int>& v)
{int begin = 0;int end = v.size() - 1;while (begin < end){int mini = begin;int maxi = begin;for (int i = begin; i <= end; ++i){if (v[mini] > v[i])mini = i;if (v[maxi] < v[i])maxi = i;}if (maxi == begin)maxi = mini;swap(&v[mini], &v[begin]);swap(&v[maxi], &v[end]);begin++;end--;}
}
特性总结
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
选择排序之堆排序
思路:通过使用大堆或者小堆的思路,将数组进行排序
1.排升序建大堆,排降序建小堆
2.升序为例,先建一个大堆(双亲节点都大于左右孩子,根节点的值最大)
3.将数组最后一个位置的值和第一个位置的值交换
4.堆中除了最后一个节点,其余的节点进行调整,调整为新的大堆,将新的大堆的根节点值和倒数第二个节点的值交换
5.以此类推,直到当前新堆的范围为1停止
6.堆排序完成
void adjustDown(int* a, int n, int parent) {int child = parent * 2 + 1;while (child < n){if (child+1 < n && a[child] < a[child + 1]) {child++;}if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}
void HeapSort(int* a, int n) {//1、建堆//parent = (child-1)/2for (int i = (n-1-1)/2; i >= 0; i--){adjustDown(a, n, i);}//2、堆排序int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);end--;adjustDown(a, end, 0);}
}
时间复杂度
O(nlogn)
特性总结
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
交换排序之冒泡排序
思想:就是从前往后,依次判断当前位置的值和后一个位置的值关系,如果当前值大于后一个位置的值,就进行交换,这样将最大的值就放到的最后面,依次让数组的范围从后往前减小,循环遍历数组,就可完成排序
void BobbleSort(int* v, int size)
{int exchage = 0;for (int i = 0; i < size ; ++i){for (int j = 0; j < size - i - 1; ++j){if (v[j] > v[j + 1]){swap(v[j], v[j + 1]);exchage = 1;}}if (exchage == 0)break;}
}
特性总结
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
交换排序之快速排序
hoare版本
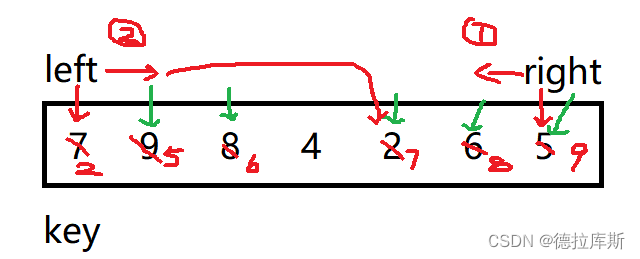
思想:将某个元素作为基准值,数组被该元素分为两个子数组,左子数组中的值均小于基准值,右子数组中的值均大于基准值,左右子数组重复上述过程,最终实现排序
做法:
1.先设置数组的第一个元素为基准值,设置第一个位置为左,最后一个位置为右
2.右先走,找比基准值小的,左后走,找比基准值大的
3.交换左右两个位置的值
4.右继续向左走,左继续向右走
以上的条件都是在左小于右的基础上进行的
5.如果相遇则将基准值和相遇值交换,函数返回相遇点
int _QuickSort(int* v, int left, int right)
{int k = left;while (left < right){//从右往左遍历,找比k小的数while (left < right && v[right] >= v[k]){right--;}//从左往右遍历,找比k大的数while (left < right && v[left] <= v[k]){left++;}//找到之后,进行交换swap(&v[left], &v[right]);}//如果相遇,将相遇点和数组左边的值交换swap(&v[left], &v[k]);return left;
}
void QuickSort(int* v, int left, int right)
{if (left >= right)return;int meet = _QuickSort(v, left, right);QuickSort(v, left, meet - 1);QuickSort(v, meet + 1, right);
}
挖坑法
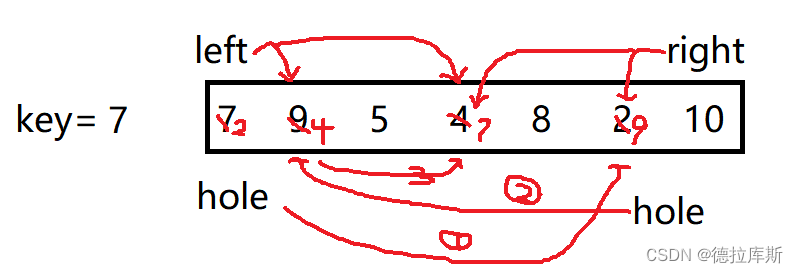
思路:
将某个元素作为基准值,数组被该元素分为两个子数组,左子数组中的值均小于基准值,右子数组中的值均大于基准值,左右子数组重复上述过程,最终实现排序
做法:
1.设置一个坑,hole为最左边的下标,一个key值
2.让右下标向左走,找比key对应值小的,让坑对应的值赋给右下标位置,并且让右下标表示为hole
3.让左下标向右走,找比key对应值大的,让坑对应的值赋给左下标位置,并且让左下标表示为hole
如果遇到左下标大于等于右下标的情况,则将key对应的值赋给相遇点
上述操作是在左小于右的范围下进行的
4.递归进行上述操作
int _QuickSort1(int* v, int left, int right)
{int hole = left;int key = v[left];while (left < right){while (left < right && v[right] >= key)right--;v[hole] = v[right];hole = right;while (left < right && v[left] <= key)left++;v[hole] = v[left];hole = left;}v[left] = key;return left;
}
void QuickSort1(int* v, int left, int right)
{if (left >= right)return;int meet = _QuickSort1(v, left, right);QuickSort1(v, left, meet - 1);QuickSort1(v, meet + 1, right);
}
双指针法
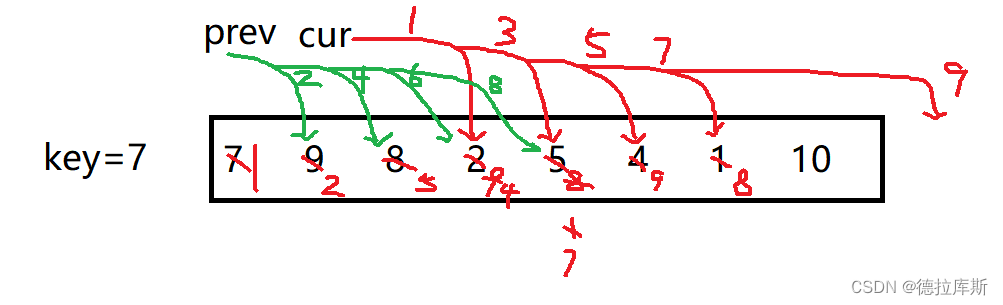
思想:和hoare版本和hole版本相似,都是将当前数组分为两个子数组,递归进行排序
做法:
1.设置key等于数组的左下标,left和right分别是数组的最左和最右,设置prev为左,prev的下一个为cur
2.先让cur向右走,找比key对应的值小的数
3.让prev++,交换prev和cur对应的两个数
4.继续上述操作
5.当cur超出right范围时,停止循环,让key和prev对应的值交换
int _QuickSort2(int* v, int left, int right)
{int prev = left;int cur = left + 1;int key = left;while (cur <= right){if (v[cur] < v[key]){prev++;swap(&v[prev], &v[cur]);}cur++;}swap(&v[key], &v[prev]);return prev;
}
void QuickSort(int* v, int left, int right)
{if (left >= right)return;int meet = _QuickSort2(v, left, right);QuickSort(v, left, meet - 1);QuickSort(v, meet + 1, right);
}
快速排序的优化1,增加三数取中
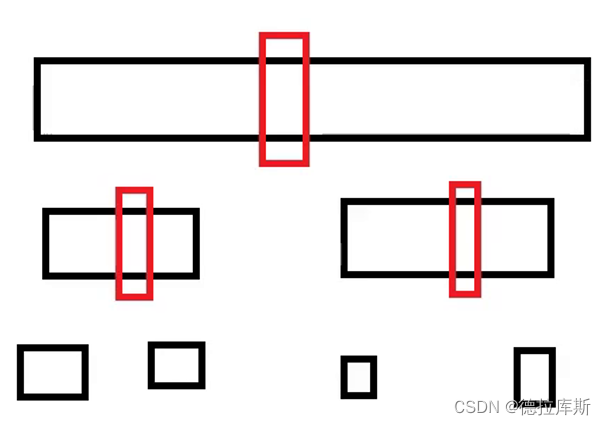
快速排序由于其思想是:根据基准值将数组划分为两个子区间,通过不断的划分子区间将其进行排序,但是当被排序数组是有序的,那么就会退化成下面图示的情况,导致复杂度为O(n2)。
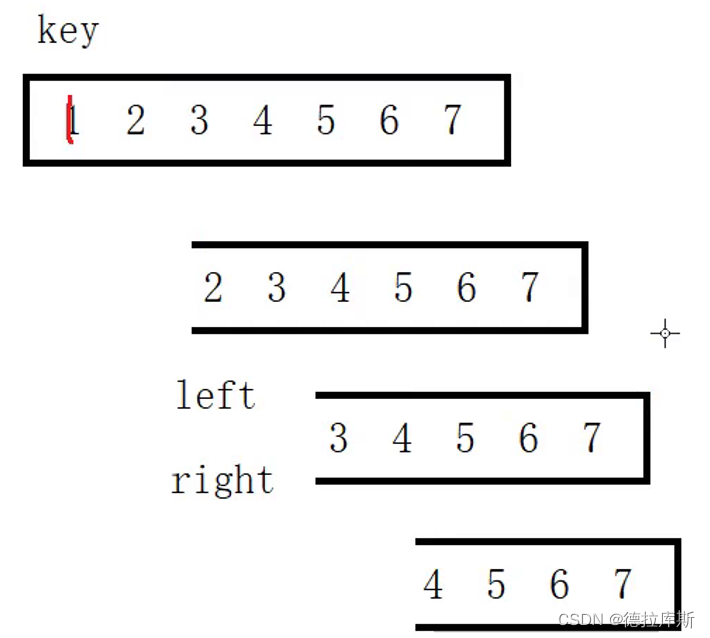
使用三数取中的方式,将数组可以平均二分,从而提高效率
//三数取中算法
int SelectMidIndex(int* v, int left, int right)
{int mid = left + (right - left) >> 1;if (v[left] > v[mid]){if (v[right] < v[mid])return mid;else if (v[right] > v[left])return left;else return right;}else //v[left] < v[mid]{if (v[right] > v[mid])return mid;else if (v[right] < v[left])return left;else return right;}
}
//hoare版本
int _QuickSort(int* v, int left, int right)
{int mid = SelectMid(v, left, right);swap(v[mid], v[left]);int k = left;while (left < right){//从右往左遍历,找比k小的数while (left < right && v[right] >= v[k]){right--;}//从左往右遍历,找比k大的数while (left < right && v[left] <= v[k]){left++;}//找到之后,进行交换swap(&v[left], &v[right]);}//如果相遇,将相遇点和数组左边的值交换swap(&v[left], &v[k]);return left;
}//hole版本
int _QuickSort1(int* v, int left, int right)
{int mid = SelectMid(v, left, right);swap(v[mid], v[left]);int hole = left;int key = v[left];while (left < right){while (left < right && v[right] >= key)right--;v[hole] = v[right];hole = right;while (left < right && v[left] <= key)left++;v[hole] = v[left];hole = left;}v[left] = key;return left;
}//双指针法
int _QuickSort2(int* v, int left, int right)
{int mid = SelectMidIndex(v, left, right);swap(&v[mid], &v[left]);int prev = left;int cur = left + 1;int key = left;while (cur <= right){if (v[cur] < v[key] && ++prev != cur)swap(&v[prev], &v[cur]);cur++;}swap(&v[key], &v[prev]);return prev;
}
快速排序的优化2,将递归算法改为非递归算法
我们可以将递归的快速排序算法改为非递归的方法,采用栈的数据结构作为辅助
思想:把之前递归版本的方法,通过循环放入栈来实现
做法:
- 将当前数组的左右下标都放入栈中
- 判断栈是否为为空,若不为空,则出栈,进行快速排序获取基准值的位置
- 通过基准值将当前数组再次划分为左右两个子数组
- 判断划分完之后的数组是否需要再次划分(判断条件是数组大小是否为1)
int _QuickSort1()
{//此处可以使用hoare,hole,双指针法
}
void QuickSort(int* v, int left, int right)
{stack<int> s;//先push右边界,再push左边界,这样后序取栈顶元素时的顺序就是左-->右s.push(right);s.push(left);while(!s.empty()){int begin = s.top();s.pop();int end = s.top();s.pop();//此时需要使用快速排序的函数,找中间值int meet = _QuickSort1(a, begin, end);//此时本质上是通过meet将数组分为了[begin,meet-1]和[meet+1,end]两部分,需要判断是否继续放入栈中if(meet-1 > begin){s.push(meet-1);s.push(begin);}if(end > meet + 1){s.push(end);s.push(meet+1);}}
}
快速排序的性能总结
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
归并排序
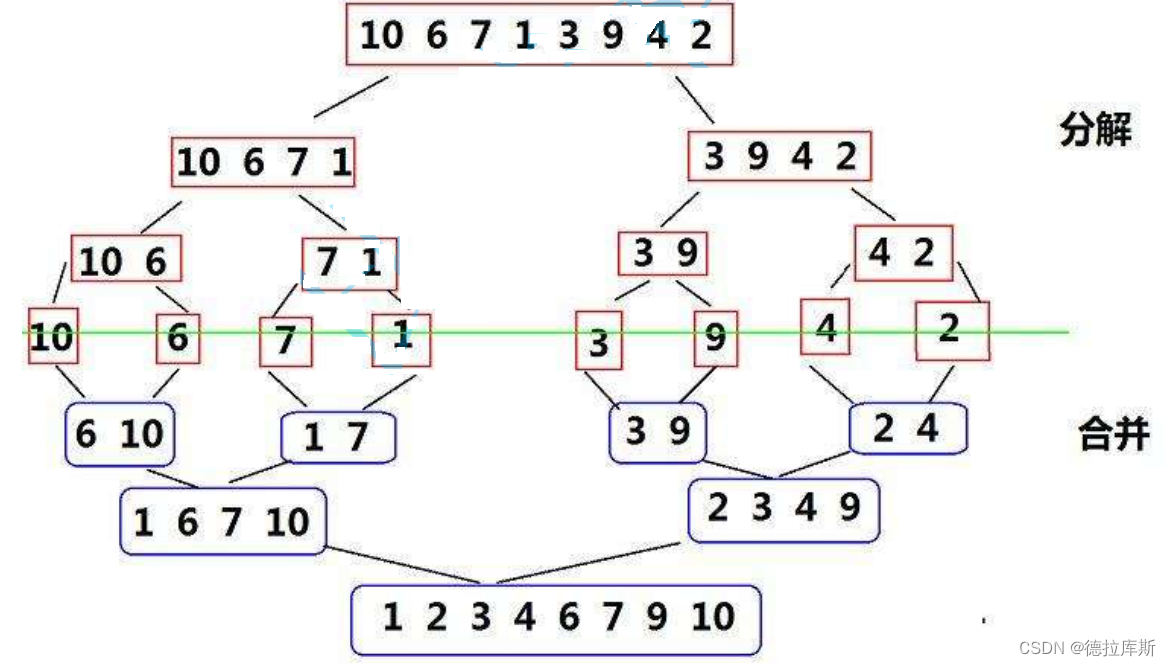
思路:采用分治法的思想,将已有的子序列合并,得到完全有序的序列,让每个子序列有序,再让两个有序列表合并为一个有序列表,称为二路归并
做法:
- 将一个数组递归分解成左右大小皆为1的数组
- 再对其进行排序(合并两个有序数组)
- 将合并好的数组回写到原数组中
void _MargeSort(int* v, int left, int right, int* tmp)
{if (left >= right)return;int mid = left + (right - left)/2;_MargeSort(v, left, mid, tmp);_MargeSort(v, mid + 1, right, tmp);int begin1 = left;int end1 = mid;int begin2 = mid + 1;int end2 = right;int index = begin1;while (begin1 <= end1 && begin2 <= end2){if (v[begin1] < v[begin2])tmp[index++] = v[begin1++];else tmp[index++] = v[begin2++];}while(begin1 <= end1)tmp[index++] = v[begin1++];while (begin2 <= end2)tmp[index++] = v[begin2++];for (int i = left; i <= right; ++i)v[i] = tmp[i];
}
void MargeSort(int* v, int n)
{int left = 0;int right = n-1;int* tmp = (int*)malloc(n * sizeof(int*));_MargeSort(v, left, right, tmp);free(tmp);
}
归并排序特性总结
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
相关文章:

【数据结构】常见的排序算法
常见的排序算法 常见的排序算法插入排序之直接插入排序时间复杂度特性总结 插入排序之希尔排序时间复杂度 选择排序之直接选择排序特性总结 选择排序之堆排序时间复杂度特性总结 交换排序之冒泡排序特性总结 交换排序之快速排序hoare版本挖坑法双指针法快速排序的优化1…...
CentOS 安装 Jenkins
本文目录 1. 安装 JDK2. 获取 Jenkins 安装包3. 将安装包上传到服务器4. 修改 Jenkins 配置5. 启动 Jenkins6. 打开浏览器访问7. 获取并输入 admin 账户密码8. 跳过插件安装9. 添加管理员账户 1. 安装 JDK Jenkins 需要依赖 JDK,所以先安装 JDK1.8。输入以下命令&a…...

前端如何设置表格边框样式和单元格间距?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 实现思路⭐ 代码演示⭐ 注意事项⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发感兴…...
Ubuntu 22.04安装搜狗输入法
Ubuntu 22.04安装搜狗输入法 ubtuntu 22.04安装搜狗输入法 1. 添加中文语言支持2. 安装fcitx输入法框架3. 设置fcitx为系统输入法4. 设置fcitx开机启动,并卸载ibus输入法框架5. 安装搜狗输入法6. 重启电脑,调出搜狗输入法 1. 添加中文语言支持 Setti…...

【C++】初阶 --- 内联函数(inline)
文章目录 🥞内联函数🍟1、C语言实现"宏函数"🍟2、内联函数的概念🍟3、内联函数的特性🍟4、总结 🥞内联函数 🍟1、C语言实现"宏函数" 🥰用C语言先来实现普通的…...
VGGNet剪枝实战:使用VGGNet训练、稀疏训练、剪枝、微调等,剪枝出只有3M的模型
摘要 本文讲解如何实现VGGNet的剪枝操作。剪枝的原理:在BN层网络中加入稀疏因子,训练使得BN层稀疏化,对稀疏训练的后的模型中所有BN层权重进行统计排序,获取指定保留BN层数量即取得排序后权重阈值thres。遍历模型中的BN层权重&am…...

【iOS】GCD深入学习
关于GCD和队列的简单介绍请看:【iOS】GCD学习 本篇主要介绍GCD中的方法。 栅栏方法:dispatch_barrier_async 我们有时候需要异步执行两组操作,而且第一组操作执行完之后,才能开始执行第二组操作,当然操作组里也可以包含一个或者…...

Webpack开启本地服务器;HMR热模块替换;devServer配置;开发与生成环境的区分与配置
目录 1_开启本地服务器1.1_开启本地服务器原因1.2_webpack-dev-server 2_HMR热模块替换2.1_认识2.2_开启HMR2.3_框架的HMR 3_devServer配置3.1_host配置3.2_port、open、compress 4_开发与生成环境4.1_如何区分开发环境4.2_入口文件解析4.3_区分开发和生成环境配置 1_开启本地服…...

opencv 31-图像平滑处理-方框滤波cv2.boxFilter()
方框滤波(Box Filtering)是一种简单的图像平滑处理方法,它主要用于去除图像中的噪声和减少细节,同时保持图像的整体亮度分布。 方框滤波的原理很简单:对于图像中的每个像素,将其周围的一个固定大小的邻域内…...
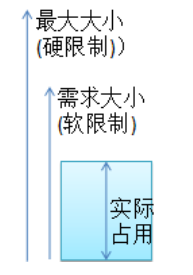
Kubernetes关于cpu资源分配的设计
kubernetes资源 在K8s中定义Pod中运行容器有两个维度的限制: 资源需求(Requests):即运行Pod的节点必须满足运行Pod的最基本需求才能运行Pod。如 Pod运行至少需要2G内存,1核CPU。(软限制)资源限额(Limits):即运行Pod期间,可能内存使用量会增加,那最多能使用多少内存,这…...

Flink读取mysql数据库(java)
代码如下: package com.weilanaoli.ruge.vlink.flink;import com.ververica.cdc.connectors.mysql.source.MySqlSource; import com.ververica.cdc.connectors.mysql.table.StartupOptions; import com.ververica.cdc.debezium.JsonDebeziumDeserializationSchema; import org…...
小程序学习(五):WXSS模板语法
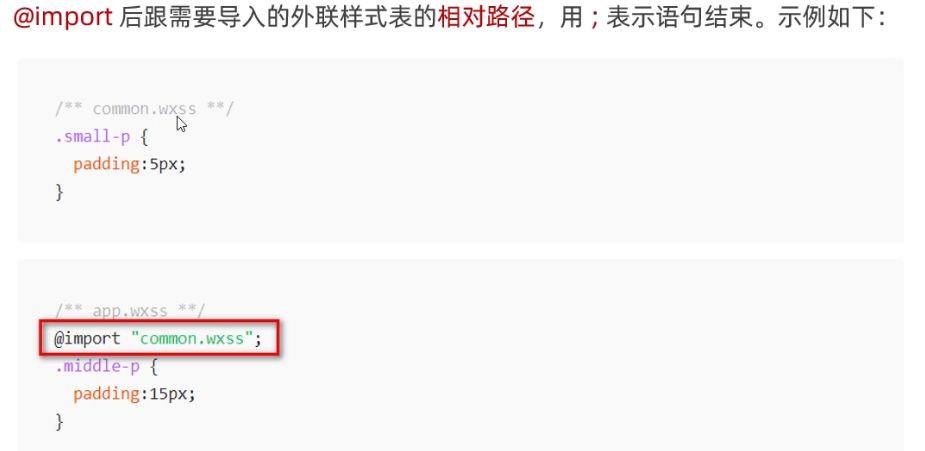
1.什么是WXSS WXSS是一套样式语言,用于美化WXML的组件样式,类似于网页开发中的CSS 2.WXSS和CSS的关系 WXSS模板样式-rpx 3.什么是rpx尺寸单位 4.rpx的实现原理 5.rpx与px之间的单位换算* WXSS模板样式-样式导入 6.什么是样式导入 使用WXSS提供的import语法,可以导入外联的样式…...

注解 @JsonFormat 与 @DateTimeFormat 的使用
文章目录 JsonFormat (双端互传)DateTimeFormat (前端传后端日期格式转化)情况一 前端是时间组件 <el-date-picker 或其他情况二 前端未设置组件 JsonFormat (双端互传) com.fasterxml.jackson.annotation.JsonFormat; 将字符串的时间转换成Date类型…...
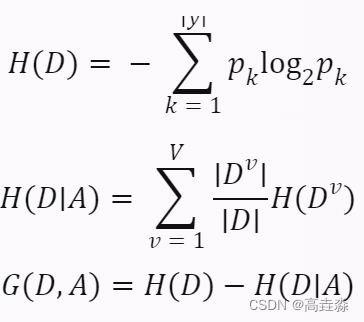
Python实现决策树算法:完整源码逐行解析
决策树是一种常用的机器学习算法,它可以用来解决分类和回归问题。决策树的优点是易于理解和解释,可以处理数值和类别数据,可以处理缺失值和异常值,可以进行特征选择和剪枝等操作。决策树的缺点是容易过拟合,对噪声和不…...

Linux文本三剑客---grep、sed、awk
目录标题 1、grep1.1 命令格式1.2命令功能1.3命令参数1.4grep实战演练 2、sed2.1 认识sed2.2命令格式2.3常用选项options2.4地址定界2.5 编辑命令command2.6用法演示2.6.1常用选项options演示2.6.2地址界定演示2.6.3编辑命令command演示 3、awk3.1认识awk3.2常用命令选项3.3awk…...
局域网VoIP网络电话测试
0. 环境 ubuntu18或者ubuntu22 - SIP服务器 win10 - SIP客户端1 ubuntu18 - SIP客户端2 1. SIP服务器搭建asterisk 1.0 环境 虚拟机ubuntu18 或者ubuntu22 1.1 直接安装 sudo apt-get install asterisk 1.2 配置用户信息 分为两个部分,第一部分是修改genera…...
el-table 去掉边框(修改颜色)
原始: 去掉表格的border属性,每一行下面还会有一条线,并且不能再拖拽表头 为了满足在隐藏表格边框的情况下还能拖动表头,修改相关css即可,如下代码 <style lang"less"> .table {//避免单元格之间出现白…...

redis与MongoDB的区别
1.Redis与MongoDB的概念 1.1 MongoDB MongoDB 是由C语言编写的,是一个基于分布式文件存储的开源数据库系统。 在高负载的情况下,添加更多的节点,可以保证服务器性能。 MongoDB 旨在为WEB应用提供可扩展的高性能数据存储解决方案。 MongoDB …...

CSS设置高度
要设置 article.content 的恰当高度,您可以使用 CSS 来控制元素的外观。有几种方法可以设置元素的高度,具体取决于你的需求和布局。 以下是几种常见的方法: 1. 固定高度:你可以直接为 article.content 设置一个固定的高度值&…...

开源免费用|Apache Doris 2.0 推出跨集群数据复制功能
随着企业业务的发展,系统架构趋于复杂、数据规模不断增大,数据分布存储在不同的地域、数据中心或云平台上的现象越发普遍,如何保证数据的可靠性和在线服务的连续性成为人们关注的重点。在此基础上,跨集群复制(Cross-Cl…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
